Notions simples de rsistance des matriaux par lexemple

Notions simples de résistance des matériaux par l’exemple 1 -Détermination des efforts intérieurs(*) dans une poutre soumise a une flexion simple (*)également appelés efforts de cohésion car ils sont développés dans la poutre aprés sa mise en charge et la maintiennent en équilibre ACCESMAD- PB -2011

Portée et charges sur la poutre à étudier L’axe Ax joignant les centres de gravité des sections But de l’étude à réaliser droites s’appelle « axe neutre » Une poutre de section rectangulaire repose sur deux appuis simples. Elle est soumise à des efforts concentrés en B et C de 1000 N et 5000 N. (voir fig ci-dessus). Le poids propre de la poutre est supposé négligeable devant ces efforts. Sous l’effet des charges externes il apparaît au niveau de chaque section droite (section perpendiculaire à l’axe neutre Ax) des efforts internes qui assurent la cohésion de l’ensemble (à condition que ces derniers soient supportables par le matériau de la poutre) L’objectif de cette étude est de déterminer ces efforts internes tout le long de la poutre , Cette partie ne développe pas les calculs des déplacements (rotation des sections; déplacements verticaux et horizontaux qui sont tout aussi essentiels à connaître) Apprenons un peu de vocabulaire et quelques définitions indispensables …

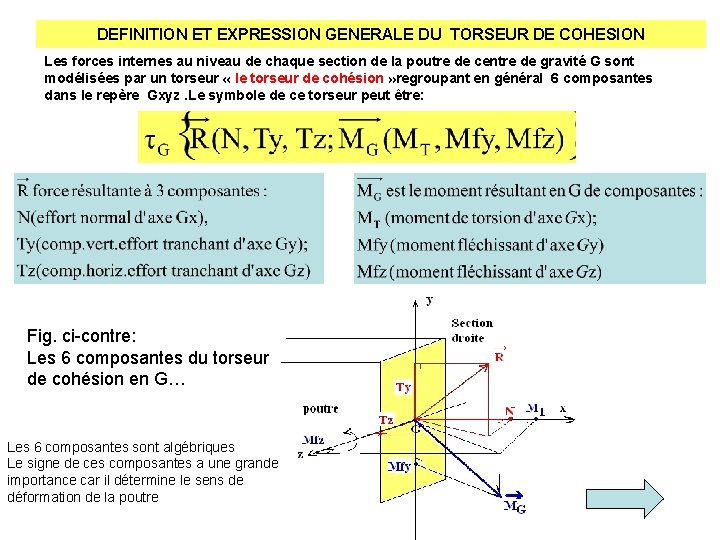
DEFINITION ET EXPRESSION GENERALE DU TORSEUR DE COHESION Les forces internes au niveau de chaque section de la poutre de centre de gravité G sont modélisées par un torseur « le torseur de cohésion » regroupant en général 6 composantes dans le repère Gxyz. Le symbole de ce torseur peut être: Fig. ci-contre: Les 6 composantes du torseur de cohésion en G… Les 6 composantes sont algébriques Le signe de ces composantes a une grande importance car il détermine le sens de déformation de la poutre

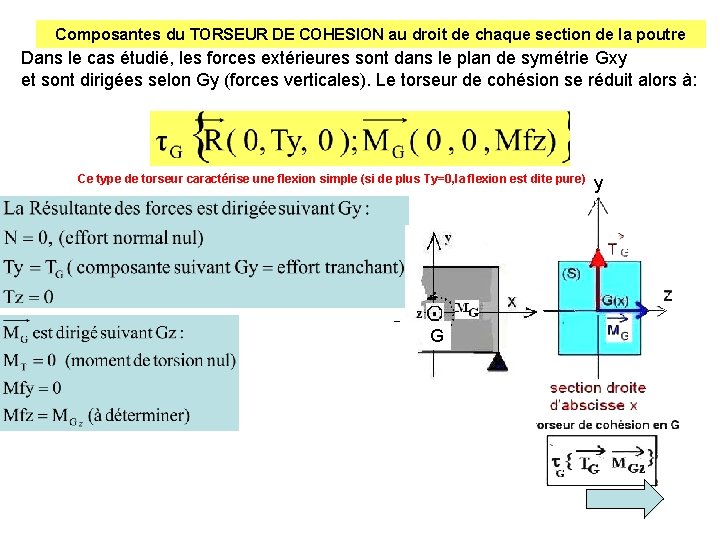
Composantes du TORSEUR DE COHESION au droit de chaque section de la poutre Dans le cas étudié, les forces extérieures sont dans le plan de symétrie Gxy et sont dirigées selon Gy (forces verticales). Le torseur de cohésion se réduit alors à: Ce type de torseur caractérise une flexion simple (si de plus Ty=0, la flexion est dite pure) G y

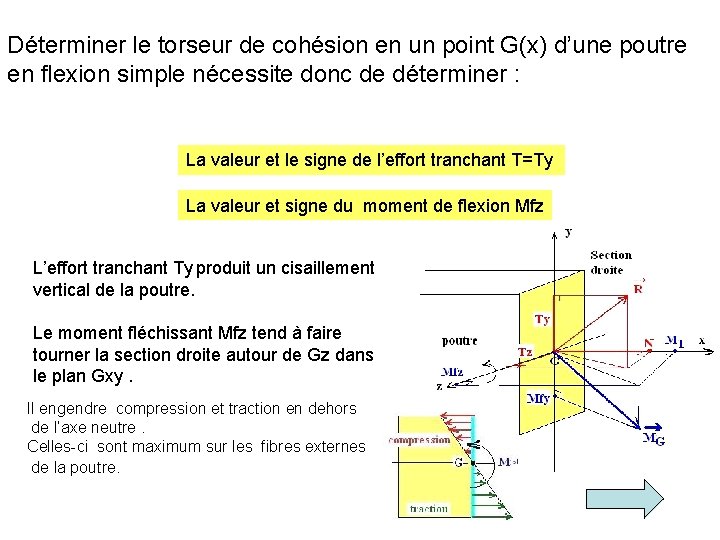
Déterminer le torseur de cohésion en un point G(x) d’une poutre en flexion simple nécessite donc de déterminer : La valeur et le signe de l’effort tranchant T=Ty La valeur et signe du moment de flexion Mfz L’effort tranchant Ty produit un cisaillement vertical de la poutre. Le moment fléchissant Mfz tend à faire tourner la section droite autour de Gz dans le plan Gxy. Il engendre compression et traction en dehors de l’axe neutre. Celles-ci sont maximum sur les fibres externes de la poutre.

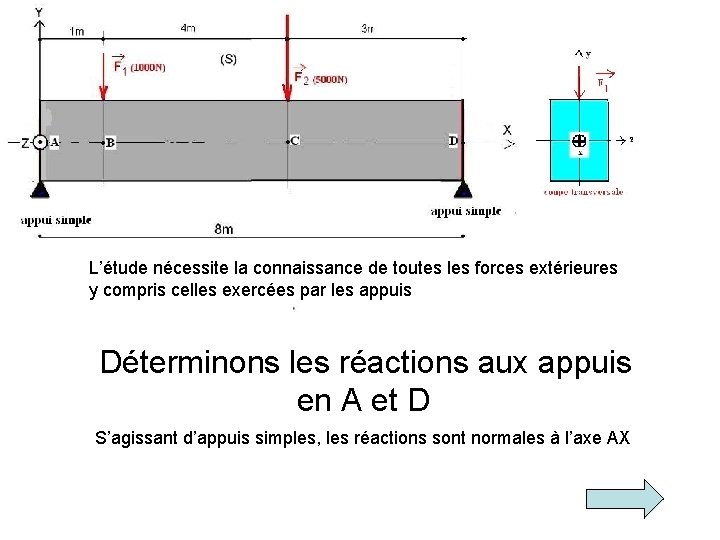
L’étude nécessite la connaissance de toutes les forces extérieures y compris celles exercées par les appuis Déterminons les réactions aux appuis en A et D S’agissant d’appuis simples, les réactions sont normales à l’axe AX

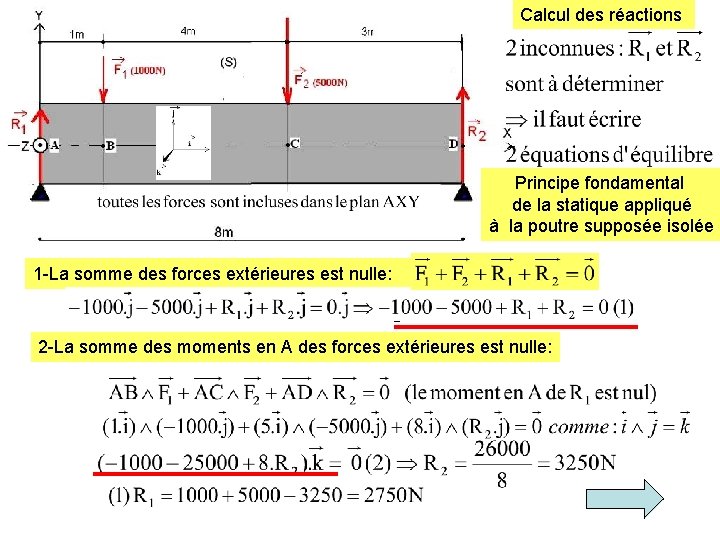
Calcul des réactions Principe fondamental de la statique appliqué à la poutre supposée isolée 1 -La somme des forces extérieures est nulle: 2 -La somme des moments en A des forces extérieures est nulle:

Principe de la détermination des composantes du torseur de cohésion le long de la poutre. Méthode la coupure fictive j k i Réaliser une coupure fictive de la poutre perpendiculaire à l’axe neutre Ax dans chaque intervalle limité par deux points d’application successifs de forces (soit en G 1, G 2, G 3) Chaque coupure permet d’ isoler fictivement une partie gauche et une partie droite de la poutre. On conviendra que les forces internes (ou de cohésion) au niveau de la coupure sont celles exercées par la partie droite de la poutre sur la partie gauche (convention A) (permuter les mots « droite » et « gauche » pour avoir la convention B) Pour chaque coupure écrire que le torseur de cohésion en G est l’opposé du torseur des forces extérieures appliquées à gauche de celle-ci …(égalité 1) …ou que le torseur de cohésion en G est égal au torseur des forces extérieures appliquées sur le tronçon de droite. (égalité 2) (choisir l’égalité qui simplifie le mieux les calculs)

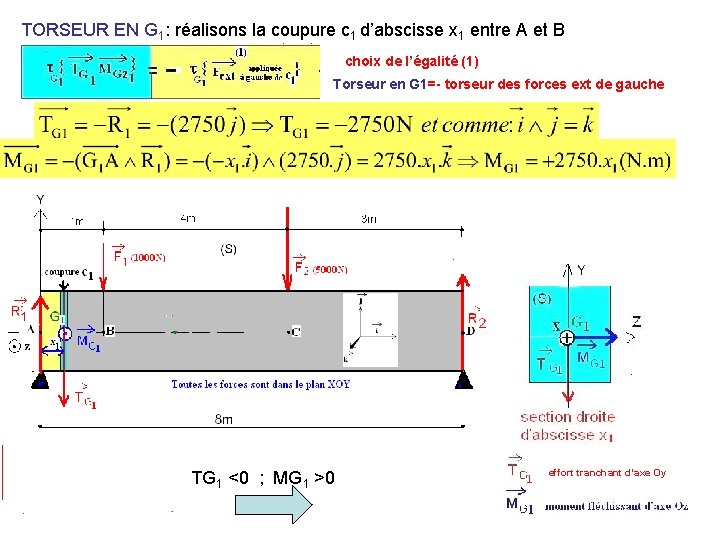
TORSEUR EN G 1: réalisons la coupure c 1 d’abscisse x 1 entre A et B choix de l’égalité (1) Torseur en G 1=- torseur des forces ext de gauche TG 1 <0 ; MG 1 >0 effort tranchant d’axe Oy

TORSEUR EN G 2: réalisons la coupure c 2 d’abscisse x 2 entre B et C Torseur en G 2 = -torseur des forces de gauche(1) TG 2<0 ; MG 2>0 effort tranchant d’axe Oy

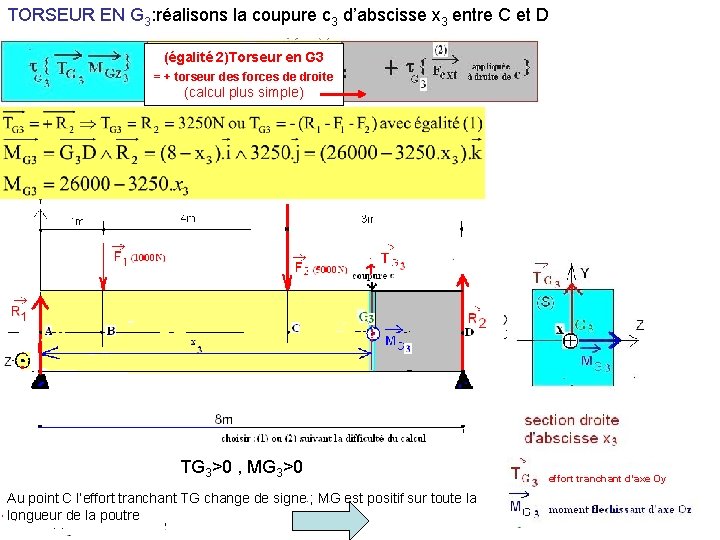
TORSEUR EN G 3: réalisons la coupure c 3 d’abscisse x 3 entre C et D (égalité 2)Torseur en G 3 = + torseur des forces de droite (calcul plus simple) TG 3>0 , MG 3>0 Au point C l’effort tranchant TG change de signe ; MG est positif sur toute la longueur de la poutre effort tranchant d’axe Oy

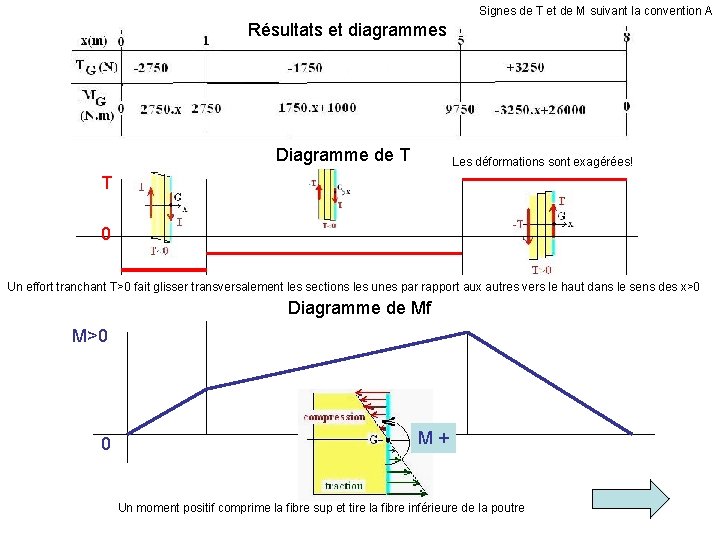
Signes de T et de M suivant la convention A Résultats et diagrammes Diagramme de T Les déformations sont exagérées! T 0 Un effort tranchant T>0 fait glisser transversalement les sections les unes par rapport aux autres vers le haut dans le sens des x>0 Diagramme de Mf M>0 0 M + Un moment positif comprime la fibre sup et tire la fibre inférieure de la poutre

Compléments mathématiques Intégration Dérivation 1 -relation entre T et M : Les fonctions MG(x) sont affines et TG(x) est égal au coefficient directeur de M (au signe prés!). On est donc conduit à écrire: 2 -Calcul des moments par intégration de la fonction T(x): L’intégration de la relation précédente entre C et D de l’axe Ax conduit par exemple à : Ce qui permet d’évaluer MC connaissant T=3250 N Cette méthode de détermination de M est plus rapide en particulier lorsque les charges appliquées sont réparties

Remarque sur la structure étudiée (poutre en flexion sur deux appuis simples ) Chaque appui simple n’apportent qu’ 1 inconnue (réaction verticale) au problème de statique Il ya donc deux inconnues au total à déterminer. Deux équations d’équilibre suffisent pour les calculer. Les inconnues sont statiquement déterminées La structure est dite isostatique Remarquer que dans ce cas, les réactions comme les forces internes sont indépendantes dimensions de la section de la poutre et de la nature du matériau. . Au contraire, lorsque le nombre d’inconnues est supérieur au nombre d’équations d’équilibre, la structure est dite hyperstatique. Les inconnues dépendent des sollicitations extérieures mais aussi de la déformation de la structure. Les caractéristiques géométriques de la structure et celles du matériau sont nécessaires pour résoudre le problème plus complexe. Système hyperstatique : Poutre encastrée à une extrémité et posée sur un appui simple de l’autre. La réaction de l’appui dépend de la déformation de la poutre