Notes on Sequence Binary Decision Diagrams Relationship to

Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations Shuhei Denzumi 1, Ryo Yoshinaka 2, 1, Shin-ichi Minato 1, 2, and Hiroki Arimura 1 1) Hokkaido University 2) JST ERATO Minato Discrete Structure Manipulation System Project

Background Researches on string processing become active. Massive online data: The internet and sensing networks. String matching and string mining problems. Data mining Input data should be represented in compact form Computation under compressed structure is needed Input Compress Data Structure Operation Result Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

Manipulatable & Compact Manipulatable Compact data structure Represent data in compressed form Have operations to manipulate data in compacted style Get much attention for recent years Binary Decision Diagram (BDD) LSI area Deterministic Finite Automata (DFA) Natural Language Processing area Input Compaction Data Structure D 1 Operation D 2 Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011 D 3

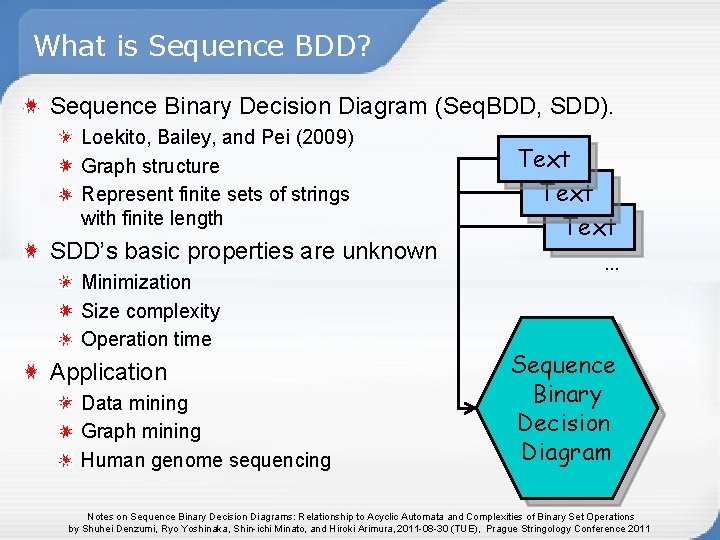
What is Sequence BDD? Sequence Binary Decision Diagram (Seq. BDD, SDD). Loekito, Bailey, and Pei (2009) Graph structure Represent finite sets of strings with finite length SDD’s basic properties are unknown Minimization Size complexity Operation time Application Data mining Graph mining Human genome sequencing Text … Sequence Binary Decision Diagram Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

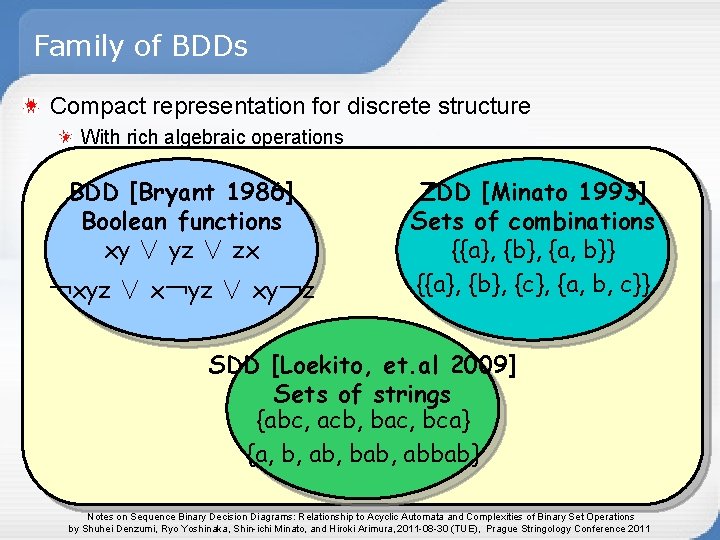
Family of BDDs Compact representation for discrete structure With rich algebraic operations BDD [Bryant 1986] Boolean functions xy ∨ yz ∨ zx ￢xyz ∨ x￢yz ∨ xy￢z ZDD [Minato 1993] Sets of combinations {{a}, {b}, {a, b}} {{a}, {b}, {c}, {a, b, c}} SDD [Loekito, et. al 2009] Sets of strings {abc, acb, bac, bca} {a, b, ab, bab, abbab} Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

Result Relationship to Acyclic Deterministic Finite Automata (ADFA) Translation from an SDD to an ADFA and vice versa An SDD is never larger than an ADFA An SDD can be |Σ| times smaller than an ADFA Computational complexity of binary set operations Generalize eight set operations Tight analysis on time complexity for binary set operation algorithm Experimental results SDDs can be smaller than ADFAs Binary operation time Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

Preliminary Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

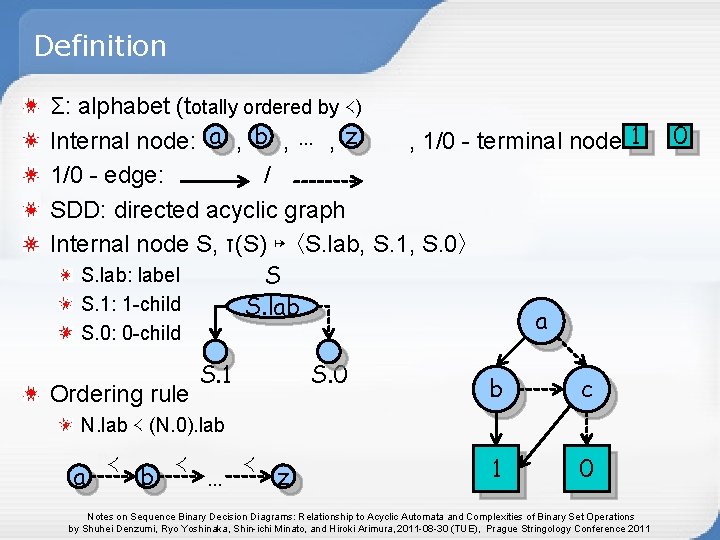
Definition Σ: alphabet (totally ordered by ≺) Internal node: a , b , … , z , 1/0 - terminal node: 1 1/0 - edge: / SDD: directed acyclic graph Internal node S, τ(S) ↦ 〈S. lab, S. 1, S. 0〉 S. lab: label S S. 1: 1 -child S. lab a S. 0: 0 -child Ordering rule S. 1 S. 0 b c 1 0 N. lab ≺ (N. 0). lab a ≺ b ≺ … ≺ z Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011 /0

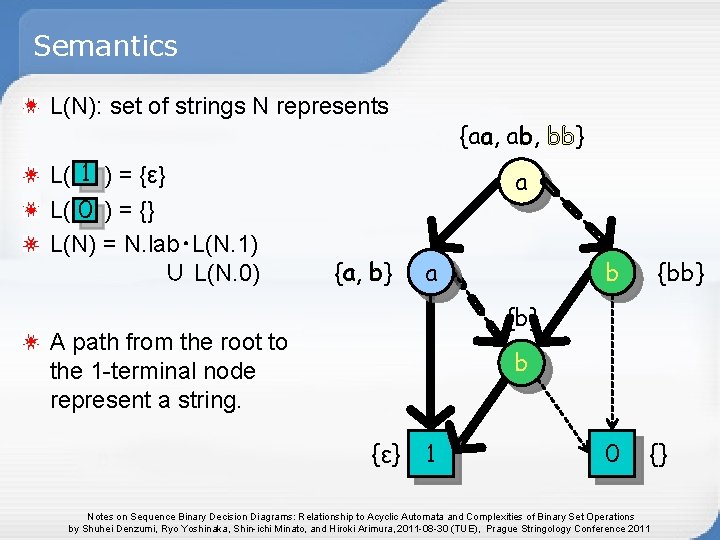
Semantics L(N): set of strings N represents L( 1 ) = {ε} L( 0 ) = {} L(N) = N. lab・L(N. 1) ∪ L(N. 0) {aa, ab, bb} a {a, b} a {bb} b {b} A path from the root to the 1 -terminal node represent a string. b {ε} 1 0 {} Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

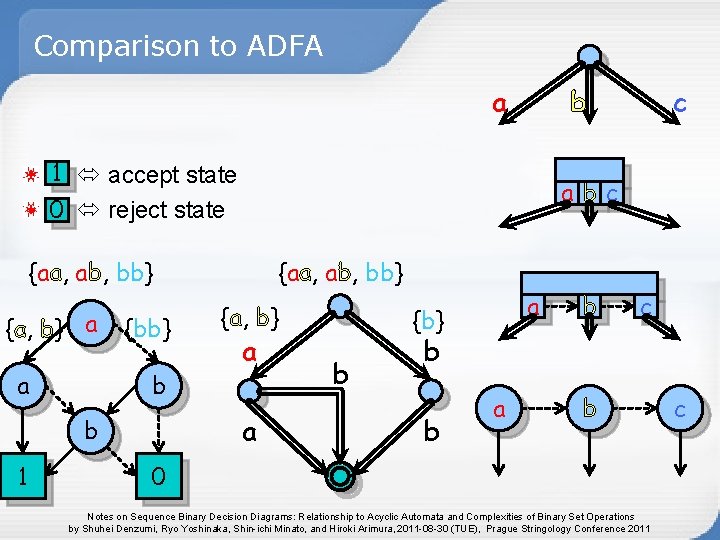
Comparison to ADFA a b 1 accept state 0 reject state abc {aa, ab, bb} {a, b} a a {bb} b 1 {aa, ab, bb} {a, b} a a b c a {b} b b c b b a b 0 Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011 c

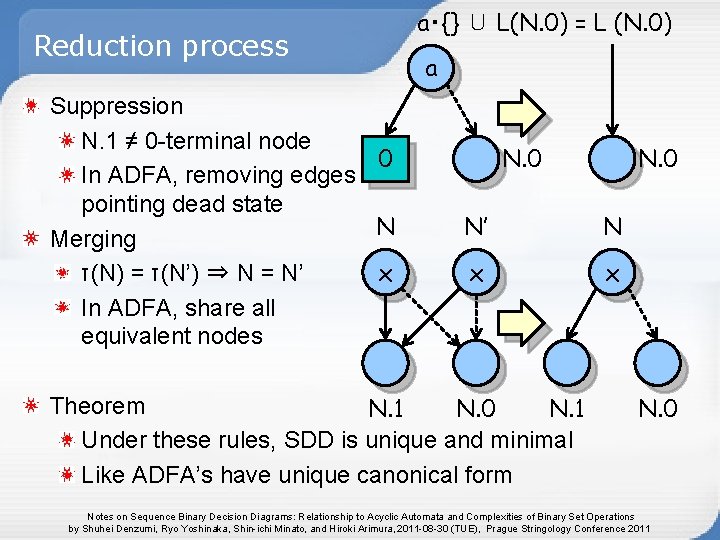
Reduction process Suppression N. 1 ≠ 0 -terminal node 0 In ADFA, removing edges pointing dead state N Merging x τ(N) = τ(N’) ⇒ N = N’ In ADFA, share all equivalent nodes a・{} ∪ L(N. 0) = L (N. 0) a N. 0 N’ N x x Theorem N. 1 N. 0 N. 1 Under these rules, SDD is unique and minimal Like ADFA’s have unique canonical form N. 0 Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

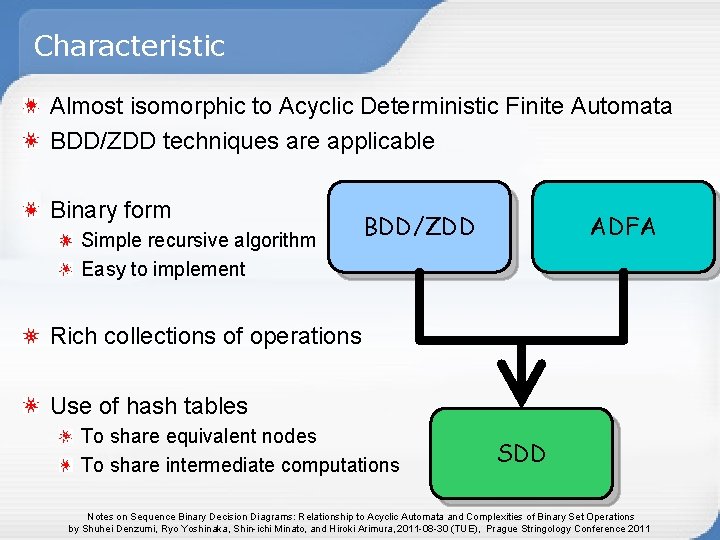
Characteristic Almost isomorphic to Acyclic Deterministic Finite Automata BDD/ZDD techniques are applicable Binary form Simple recursive algorithm Easy to implement BDD/ZDD ADFA Rich collections of operations Use of hash tables To share equivalent nodes To share intermediate computations SDD Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

Relationship to Acyclic Automata Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

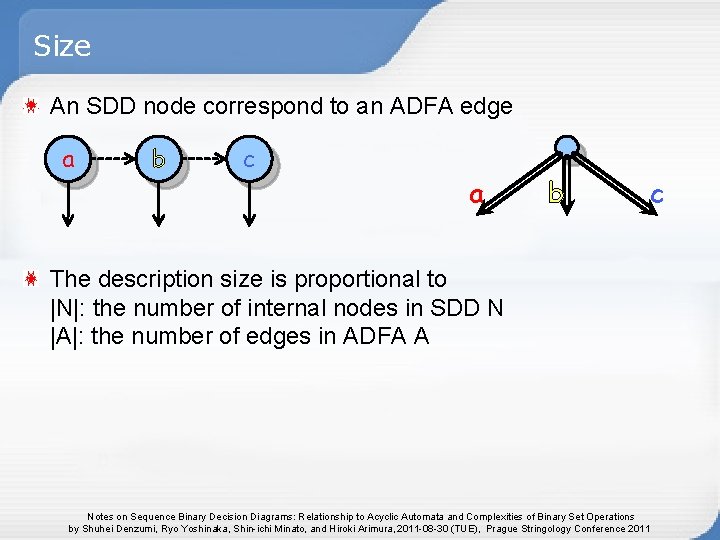
Size An SDD node correspond to an ADFA edge a b c a b The description size is proportional to |N|: the number of internal nodes in SDD N |A|: the number of edges in ADFA A Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011 c

Theorem: Size compare For equivalent an SDD and an ADFA From an ADFA A to an SDD N From an SDD N to an ADFA A SDD |Σ| times can be smaller than ADFA Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

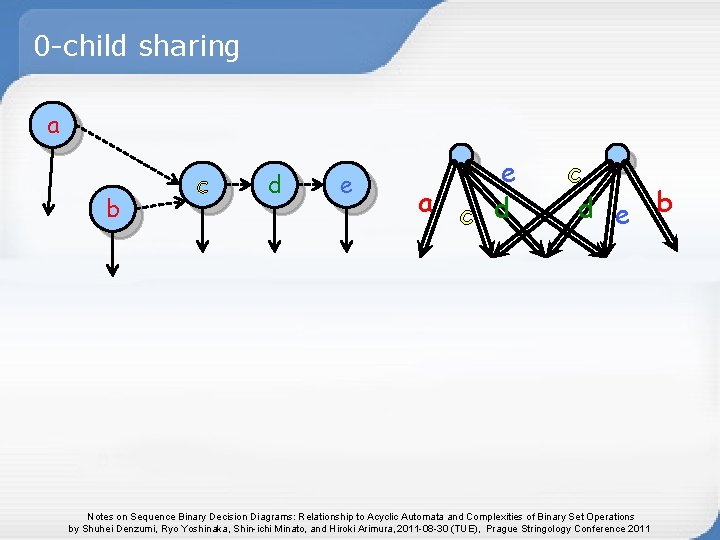
0 -child sharing a b c d e e a c d e b Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

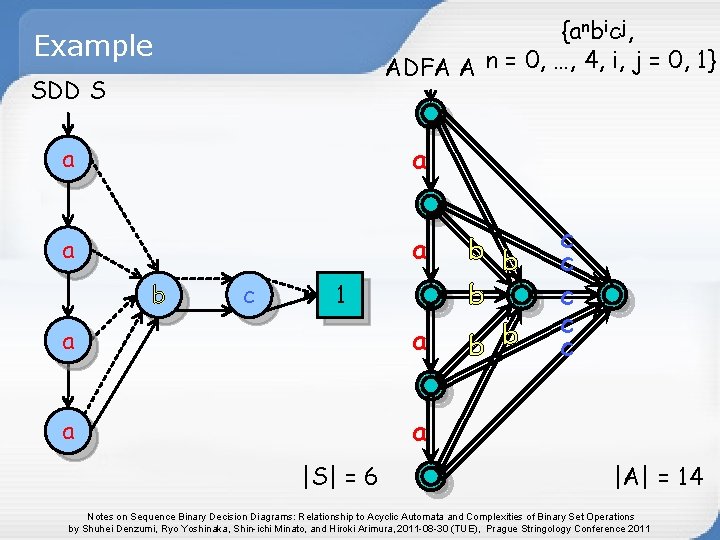
{anbicj, ADFA A n = 0, …, 4, i, j = 0, 1} Example SDD S a a b c 1 a a |S| = 6 b b b c c c |A| = 14 Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

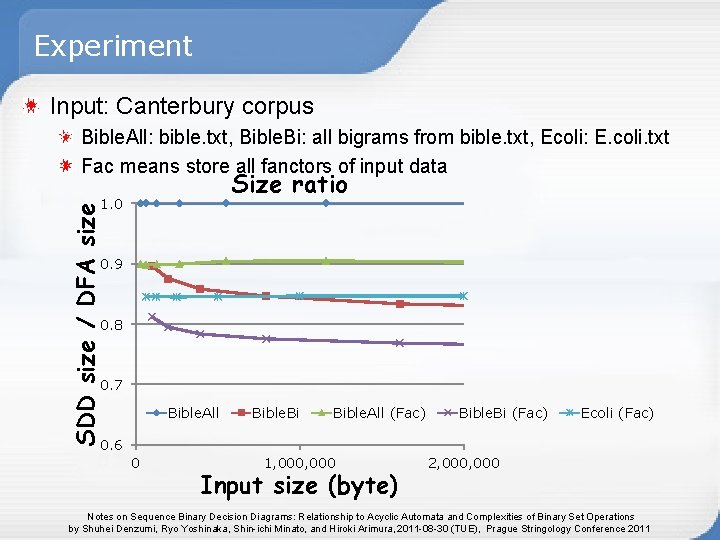
Experiment Input: Canterbury corpus Bible. All: bible. txt, Bible. Bi: all bigrams from bible. txt, Ecoli: E. coli. txt Fac means store all fanctors of input data Size ratio SDD size / DFA size 1. 0 0. 9 0. 8 0. 7 Bible. All Bible. Bi Bible. All (Fac) Bible. Bi (Fac) Ecoli (Fac) 0. 6 0 1, 000 Input size (byte) 2, 000 Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

Binary Set Operation Algorithm Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

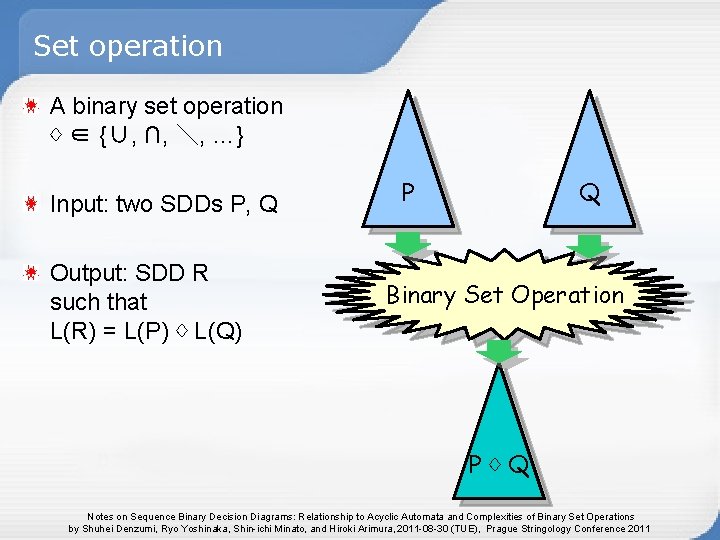
Set operation A binary set operation ♢ ∈ {∪, ∩, ＼, …} Input: two SDDs P, Q Output: SDD R such that L(R) = L(P) ♢ L(Q) P Q Binary Set Operation P♢Q Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

Apply algorithm Originally for BDD [Bryant 1986], applied to SDD Based on the definition L(N) = N. lab ・ L(N. 1) ∪ L(N. 0) In operation, (when P. lab = Q. lab) L(P) ♢ L(Q) = P. lab ・ (L(P. 1) ♢ L(Q. 1)) ∪ (L(P. 0) ♢ L(Q. 0)) P Q P♢Q a a a ♢ P 1 P 0 Q 1 Q 0 P 1♢Q 1 P 0♢Q 1 Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

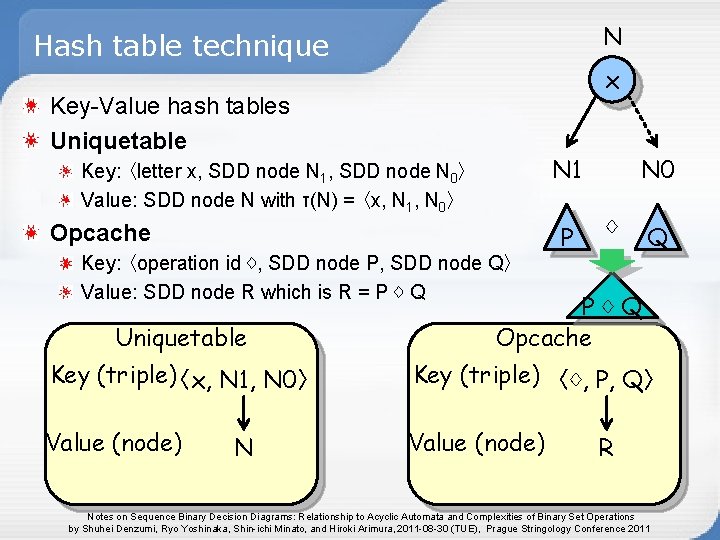
N Hash table technique x Key-Value hash tables Uniquetable Opcache Key: 〈operation id ♢, SDD node P, SDD node Q〉 Value: SDD node R which is R = P ♢ Q Uniquetable N 0 N 1 Key: 〈letter x, SDD node N 1, SDD node N 0〉 Value: SDD node N with τ(N) = 〈x, N 1, N 0〉 P ♢ Q P♢Q Opcache Key (triple)〈x, N 1, N 0〉 Key (triple) 〈♢, P, Q〉 Value (node) N R Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

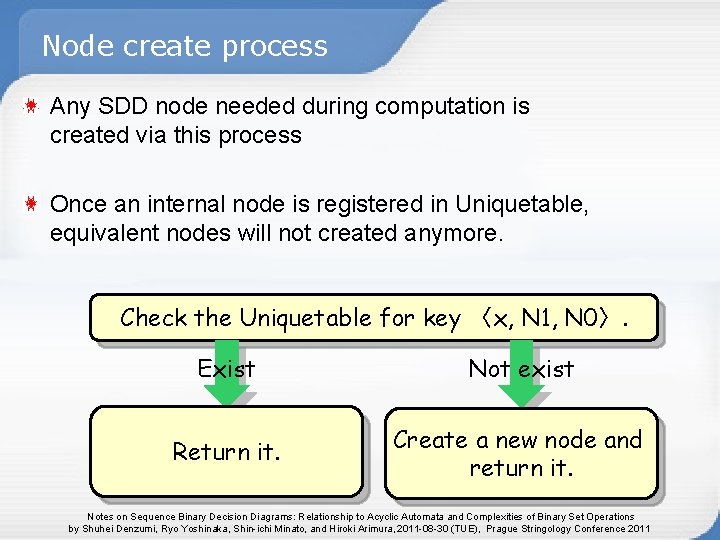
　Node create process Any SDD node needed during computation is created via this process Once an internal node is registered in Uniquetable, equivalent nodes will not created anymore. Check the Uniquetable for key 〈x, N 1, N 0〉. Exist Not exist Return it. Create a new node and return it. Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

Time complexity When P ♢ Q is executed Every operation use Opcache At most |P| × |Q| different instances of recursive calls invoke (Assume that the access time to hash tables is constant) Naïve method Prepare |P| × |Q| size table This method No useless or redundant node Theorem Worst case O(|P| |Q|) time Example needs Ω(|P| |Q|) time exist Lower and upper bound got Check the Opcache for key 〈♢, P, Q〉. Exist Not exist P ♢ Q is already done, return it. Continue to computation on 0 -side and 1 -side. Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

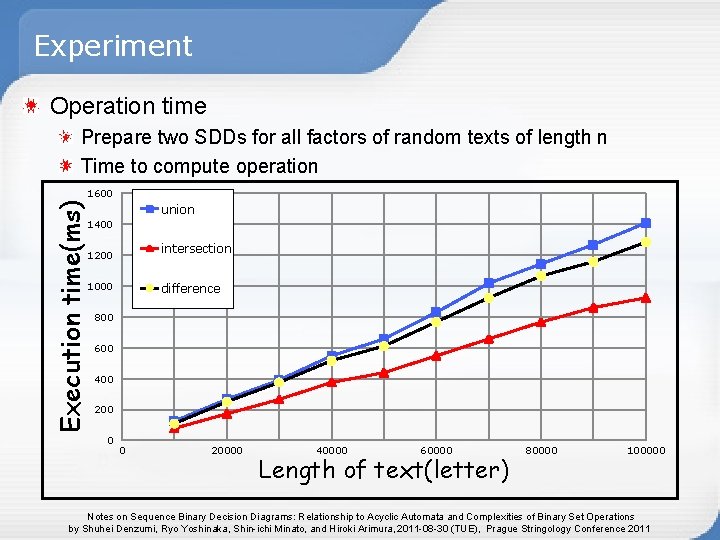
Experiment Operation time Prepare two SDDs for all factors of random texts of length n Time to compute operation Execution time(ms) 1600 union 1400 intersection 1200 1000 difference 800 600 400 200 0 0 20000 40000 60000 Length of text(letter) 80000 100000 Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

Conclusion Relationship to Acyclic Automata An SDD can be |Σ| times smaller than an ADFA For real data, SDDs are 10~20 % more compact than ADFAs Computational complexity of binary set operations Worst case time complexity is quadratic Tight time bound is analyzed In our experiment, operation time is almost linear Future work Efficient implement of various operations Propose substring index on SDD Factor SDD construction algorithm Notes on Sequence Binary Decision Diagrams: Relationship to Acyclic Automata and Complexities of Binary Set Operations by Shuhei Denzumi, Ryo Yoshinaka, Shin-ichi Minato, and Hiroki Arimura, 2011 -08 -30 (TUE), Prague Stringology Conference 2011

Thank you!