NOTES ON MULTIPLE REGRESSION USING MATRICES Tony E

NOTES ON MULTIPLE REGRESSION USING MATRICES Tony E. Smith ESE 502: Spatial Data Analysis Multiple Regression Matrix Formulation of Regression Applications to Regression Analysis

SIMPLE LINEAR MODEL Data: Parameters: Model:

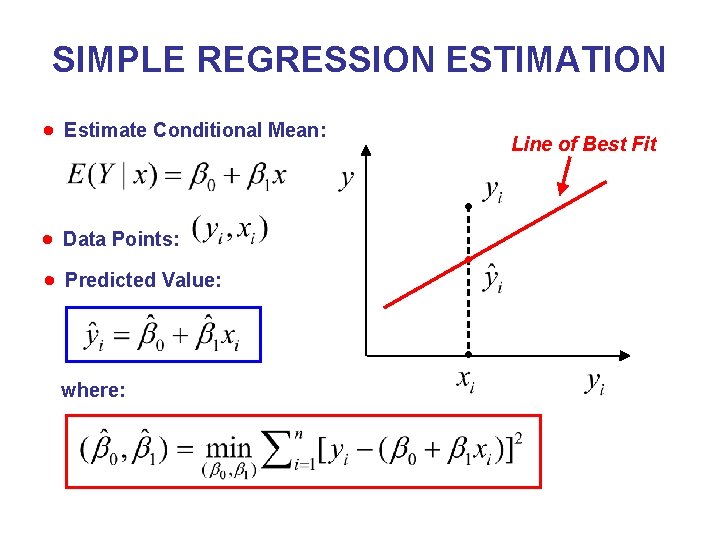
SIMPLE REGRESSION ESTIMATION Estimate Conditional Mean: Line of Best Fit Data Points: Predicted Value: where:

STANDARD LINEAR MODEL Data: Parameters: Model:

STANDARD LINEAR MODEL (k = 2) Data: Parameters: Model:

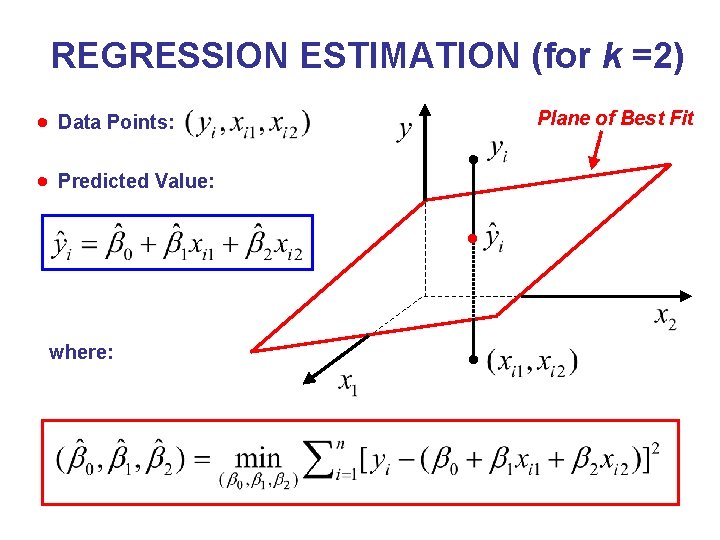
REGRESSION ESTIMATION (for k =2) Data Points: Predicted Value: Plane of Best Fit where:

MATRIX REPRESENTATION OF THE STANDARD LINEAR MODEL Vectors and Matrices: Matrix Reformulation of the Model:

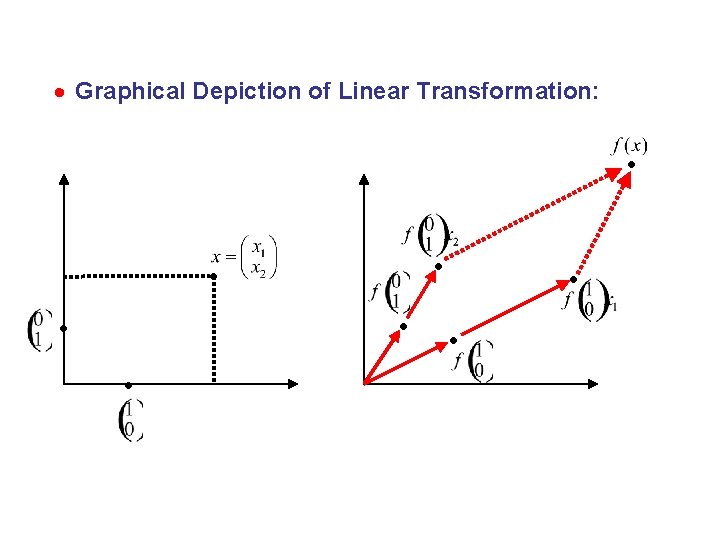
LINEAR TRANSFORMATIONS IN ONE DIMENSION Linear Function: Graphic Depiction:

LINEAR TRANSFORMATIONS IN TWO DIMENSIONS Linear Transformation:

Graphical Depiction of Linear Transformation:

SOME MATRIX CONVENTIONS Transposes of Vectors and Matrices: Symmetric (Square) Matrices: Important Example:

Row Representation of Matrices: Column Representation of Matrices:

Inner Product of Vectors: Matrix Multiplication: Transposes:

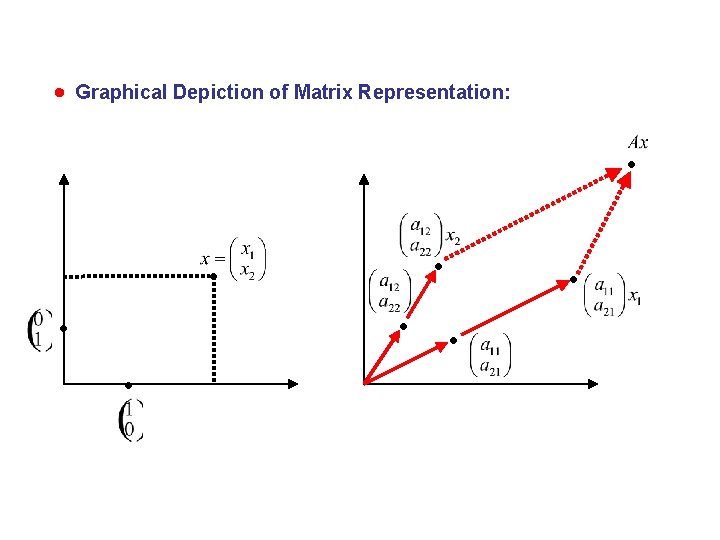
MATRIX REPRESENTATIONS OF LINEAR TRANSFORMATIONS For any Two-Dimensional Linear Transformation : with :

Graphical Depiction of Matrix Representation:

Inversion of Square Matrices (as Linear Transformations):

DETERMINANTS OF SQUARE MATRICES

NONSINGULAR SQUARE MATRICES

LEAST-SQUARES ESTIMATION General Regression Matrices: General Sum-of-Squares:

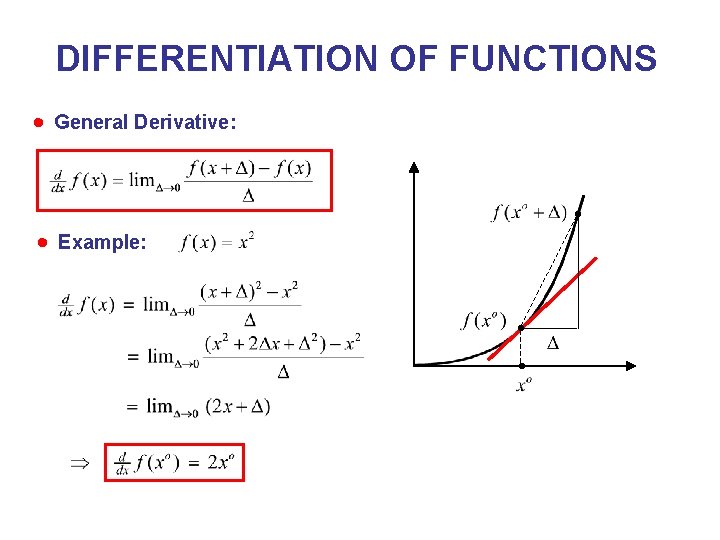
DIFFERENTIATION OF FUNCTIONS General Derivative: Example:

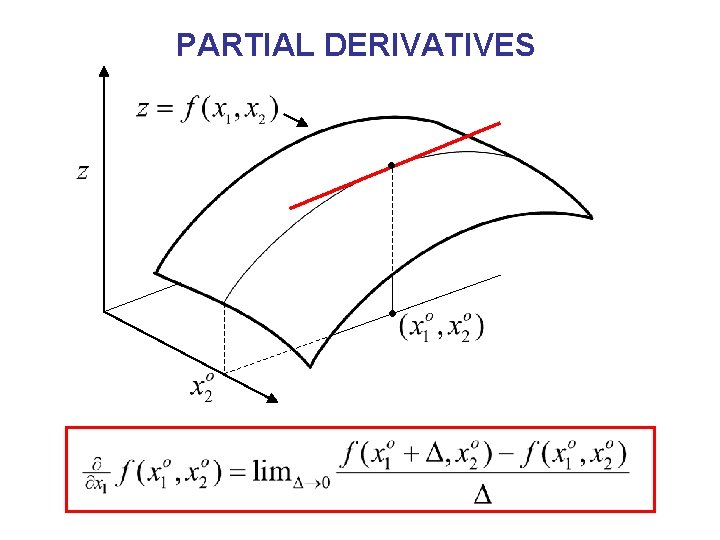
PARTIAL DERIVATIVES

VECTOR DERIVATIVES Derivative Notation for: Gradient Vector:

TWO IMPORTANT EXAMPLES Linear Functions: Quadratic Functions:

Quadratic Derivatives: Symmetric Case:

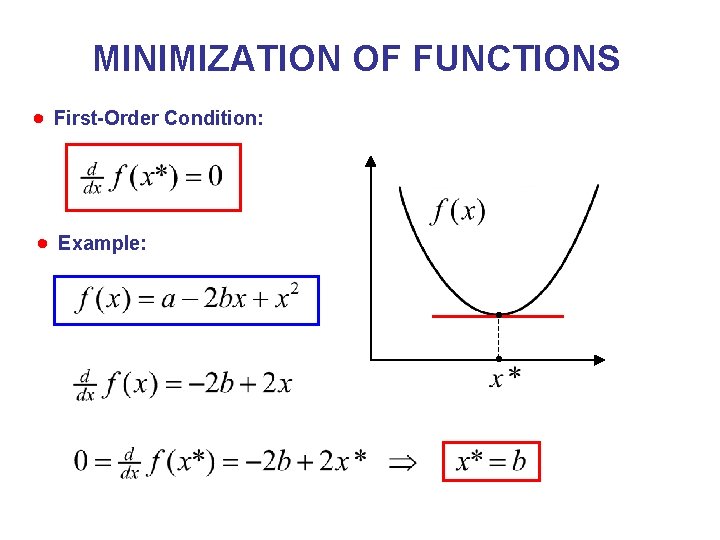
MINIMIZATION OF FUNCTIONS First-Order Condition: Example:

TWO-DIMENSIONAL MINIMIZATION

LEAST SQUARES ESTIMATION Solution for:

NON-MATRIX VERSION (k = 2) Data: Beta Estimates:

EXPECTED VALUES OF RANDOM MATRICES Random Vectors and Matrices Expected Values:

EXPECTATIONS OF LINEAR FUNCTIONS OF RANDOM VECTORS Linear Combinations Linear Transformations

EXPECTATIONS OF LINEAR FUNCTIONS OF RANDOM MATRICES Left Multiplication Right Multiplication (by symmetry of inner products):

COVARIANCE OF RANDOM VECTORS Random Variables : Random Vectors:

COVARIANCE OF LINEAR FUNCTIONS OF RANDOM VECTORS Linear Transformations: ( Left Mult ) ( Right Mult ) Linear Combinations:

TRANSLATIONS OF RANDOM VECTORS Translation: Means: Covariances:

RESIDUAL VECTOR IN THE STANDARD LINEAR MODEL Linear Model Assumption: Residual Means: Residual Covariances:

MOMENTS OF BETA ESTIMATES Linear Model: Mean of Beta Estimates: (Unbiased Estimator) Covariance of Beta Estimates:

ESTIMATION OF RESIDUAL VARIANCE Residual Variance: Residual Estimates: Natural Estimate of Variance: Bias-Correct Estimate of Variance: (Compensates for Least Squares)

ESTIMATION OF BETA COVARIANCE Beta Covariance Matrix: Beta Covariance Estimates: