Notes on Labs and Assignments Commenting Revisited n

Notes on Labs and Assignments

Commenting Revisited n You have probably been able to “get away” with poor inline documentation is labs q q n Tasks are straightforward Often only one key method is involved On assignments this is not going to work q q Bigger variety of solutions Tougher to follow as a marker (or user)

The Header Comment n It is good practice to include an initial comment in the source file for each class /* Alpha. Chars. java Author: Aaron Hunter Date: September 26, 2006 CMPT 126 - Lab 2 Provides methods to check if a string contains letters. */

Method Descriptions n It is also good practice to include a comment preceding each method /*Checks if a single character is a letter. */ public static boolean is. Alpha( char c) { if (((c >= 'a') && (c <= 'z')) || ((c >= 'A') && (c <= 'Z'))) return true; else return false; }

Another Method /* Checks if a string contains all letters. */ public static boolean is. All. Alpha(String s) { for(int i=0; i<s. length(); i++) { \ Check each character. If not a letter, \ return false. if(!is. Alpha(s. char. At(i))) return false; } \ If the loop completes without returning false, \ then everything is a letter and we should \ \ \ return true; }

Another Method /* Checks if a string contains all letters. */ public static boolean is. All. Alpha(String s) { for(int i=0; i<s. length(); i++) { if(!is. Alpha(s. char. At(i))) return false; } return true; }

Abstracting The General Problem n Given a method has. Property(Type x) q n checks if x has some property, returns true if it does Given a variable x. Array of type Type[] : n n n Does every element of x. Array have the property? Does some element of x. Array have the property? Do no elements of x. Array have the property?

Solution – All public static boolean all. Have. Property(Type[] x. Array) { for(int i=0; i<x. Array. length; i++) { if(!has. Property(x. Array[i])) return false; } return true; }

Solution – Some public static boolean some. Have. Property(Type[] x. Array) { for(int i=0; i<x. Array. length; i++) { if(has. Property(x. Array[i])) return true; } return false; }

Solution – None public static boolean none. Have. Property(Type[] x. Array) { for(int i=0; i<x. Array. length; i++) { if(has. Property(x. Array[i])) return false; } return true; }

Lab 2 – Basic Comments n Use comments q q comments before methods comments about important bits of code n n Use sub-methods q n e. g. Why are you casting a char to an int? if you are copying and pasting lots of code, maybe you need another method Make the code testable

Running Time

Speed n n When writing programs, we often want them to be fast Several things affect this: q q n The algorithm that is implemented The way the algorithm is implemented Programming language used Capabilities of the hardware We won’t worry about the 3 rd and 4 th points

Algorithm vs. Implementation n The algorithm is the step by step procedure used to solve a problem q One problem can be solved by different algorithms n q e. g. linear search vs. binary search One algorithm can be implemented in different ways in Java n e. g. linear search with a for loop vs. linear search with a while loop

Algorithm vs. Implementation n n So… the algorithm is the procedure that is used to solve the problem … the implementation of the algorithm is the way the algorithm is described in Java q n (or some other programming language) Algorithms are the kind of thing we can describe with pseudo-code – implementations are described in Java.

Implementation n For a given algorithm, there will be many ways it can be implemented q q n e. g. loop forward or backwards, order of if conditions, how to split into methods, lazy/active boolean operators… some of these affect the speed of the program No rules here: programming experience helps q so does knowledge of system architecture, compilers, interpreters, language features, …

Algorithm Analysis n n To analyze an algorithm is to determine the amount of “resources” needed for execution Typically there are two key resources: q q n Time Space (memory) We will only be concerned with running time today

Algorithm Analysis n Donald Knuth (1938 --) q q pioneer in algorithm analysis wrote “The Art of Programming” (I-III) n q q mails $2. 56 for every error found developed the Tex typesetting system bible analysis through random sampling "Beware of bugs in the above code; I have only proved it correct, not tried it. "

Algorithm Analysis n The inherent running time of an algorithm almost always overshadows the implementation q e. g. There is nothing we can do to make Power 1 run as fast as Power 2 n q (for large values of y) e. g. For sorted arrays, binary search is always faster n (for large arrays, in the worst case)

Measuring Running Time n To evaluate the efficiency of an algorithm: q We can’t just time it n q n Need something that allows us to generalize Idea: count the number of “steps” required q n Different architectures, hidden processes, etc. For an input of size n Will be measured in terms of “Big-O” notation

Measuring Running Time n We define algorithms for any input (of appropriate type) n What is the size of the input? q q n For numerical inputs… it is just the input value n For string inputs… normally the length What is a step? q Normally it is one command

Actual Running Time n Consider the following pseudocode algorithm: Given input n int[] n_by_n = new int[n][n]; for i<n, j<n set n_by_n[i][j] = random(); print “The random array is created”;

Actual Running Time n How many steps does it take for input n? q q q n n 1 step: declare an n by n array n 2 steps: put random numbers in the array 1 step: print out the final statement Total steps: n 2 + 2 Note: the extra 2 steps don’t carry the same importance as the n 2 steps q as n gets big… the extra two steps are negligible

Actual Running Time n We also think of constants as negligible q q n we want to say n 2 and c*n 2 have “essentially” the same running time as n increases more accurately: the same asymptotic running time Commercial programmers would argue here… constants can matter in practice

Actual Running Time n n But for large n, the constants don’t matter nearly as much Plug in n=1000 q q n 2+500 = 1000500 2 n 2 = 2000000 n 3 = 100000 2 n = 10301 (approx) [+500] [+100000] [+999000000] [+ 10301 ]

Big O Notation n Running time will be measured with Big-O notation Big-O is a way to indicate how fast a function grows e. g. “Linear search has running time O(n) for an array of length n” q indicates that linear search takes about O(n) steps

Big-O Notation n When we say an algorithm has running time O(n): q q q we are saying it runs in the same time as other functions with time O(n) we are describing the running time ignoring constants we are concerned with large values of n

Big-O Rules n Ignore constants: q n Ignore smaller powers: q n O(c * f(n)) = O(f(n)) O(n 3 + n) = O(n 3) Logarithms cost less than a power q q Think of log n as equvialent to n 0. 000…. 001 O(na+0. 1) > O(na log n) > O(na) e. g. O(n log n + n) = O(n log n) e. g. O(n log n +n 2) = O(n 2)

Why Big-O? n Look at what happens for large inputs q q q n small problems are easy to do quickly big problems are more interesting larger function makes a huge difference for big n Ignores irrelevant details q q Constants and lower order terms depend on implementation Don’t worry about that until we’ve got a good algorithm

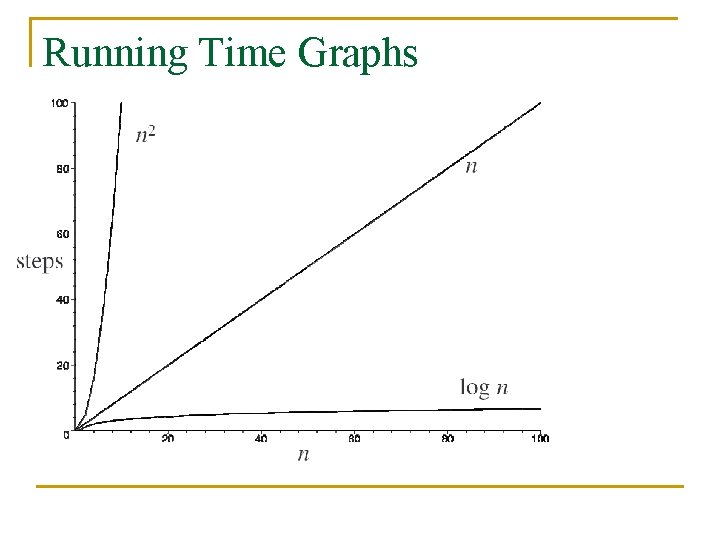
Running Time Graphs

Determining Running Time n Need to count the number of “steps” to complete q q q n need to consider the worst case for input of size n a “step” must take constant (O(1)) time Often: q q iterations of the inner loop * work per loop recursive calls * work per call

Why Does log Keep Coming Up? n n By default, we write log n for log 2 n High school math: q q n logb c = e means be = c so: log 2 n is the inverse of 2 n log 2 n is the power of 2 that gives result n

Why Does log Keep Coming Up? n Exponential algorithm – O(2 n) q n Increasing input by 1 doubles running time Logarithmic algorithm – log n q q q The inverse of doubling… Doubling input size increases running time by 1 Intuition: n O(log n) means that every step in the algorithm divides the problem size in half

Example 1: Search n Linear search: q q q n checks each element in array does some other stuff in java implementation… but just a constant number of steps O(n) - “order n” Binary search q q q chops array in half with each step n n/2 n/4 n/8 …. 2 1 takes log n steps: O(log n) - “order log n”

Example 2 n Power 1: q q n xy = x * xy-1 makes y recursive calls: O(y) Power 2: q q q xy = xy/2 * xy/2 Makes log y recursive calls: O(log y) Had to be careful not to compute xy/2 twice n n Would have created a O(y) algorithm Instead: calculated once and stored in a variable

Computational Complexity n n All of this falls in the larger field of computational complexity theory Historically: q recursion theory: what can be computed? n q not everything it turns out complexity theory: given a computable function, how much time and space are needed?

Computational Complexity n Polynomial good, exponential bad q q n n polynomial time = O(nk) for any k exponential time = basically O(2 n) This is a big jump in time Will not be bridged by “faster computers” q polynomial algorithm on modern computer n q q <1 second for large n exponential algorithm can be in the centuries 1000 times faster computers… still in the centuries

Non-Deterministic Algorithms n Allow the algorithm to “guess” a value and assume it is right q q n n Det: check if a student is enrolled in CMPT 126 Non: find a student enrolled in CMPT 126 Intuitively: finding an example is harder than checking an example The big question: Can non-deterministic polynomial algorithms be captured with deterministic ones?

Non-Deterministic Algorithms n n Commonly called the “P=NP” problem Open for 30 years Currently there is a 1 million dollar prize for a solution (from the Clay Institute) All modern cryptography and e-commerce relies on the (unproved) assumption of a solution