Notes for Algebra 1 Chapter 1 1 1

Notes for Algebra 1 Chapter 1

1 -1 Notes Algebra 1 Variables and Expressions

Algebraic Expression Consist of variables, numbers and operations.

Variables Symbols or letters used to represent unspecified numbers and values.

Term May be a number or variable or a product or quotient of numbers and variables.

Factors The quantities being multiplied in a multiplication expression

Product The answer to a multiplication expression

Exponent (power) Indicates the number of times the base is used as a factor.

Base The number that is used as a factor in an exponential expression

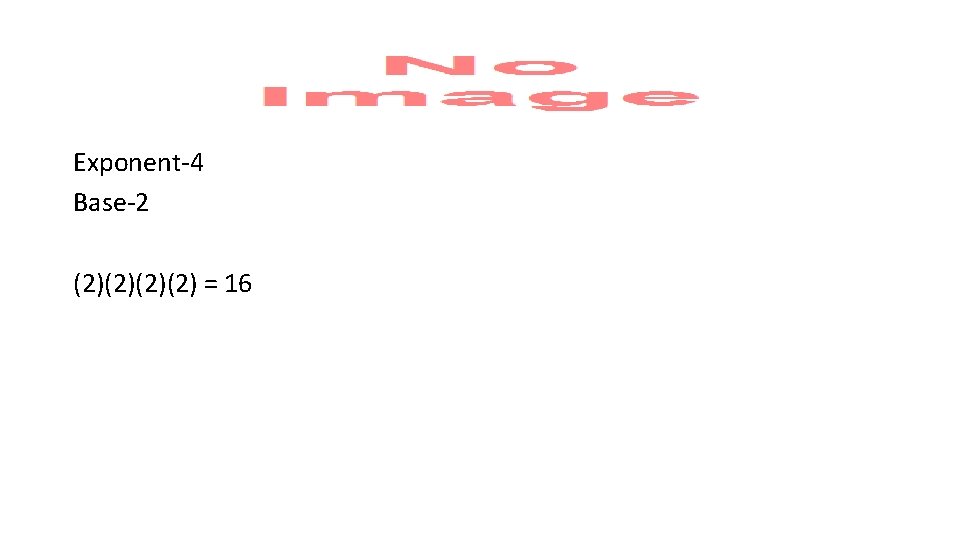
Exponent-4 Base-2 (2)(2) = 16

Example 1 pg. 5 Write a verbal expression •

Example 2 pg. 6 Write Algebraic Expressions Write an algebraic expression for each verbal expression. 1. ) 5 less than a number c 2. ) 9 plus the product of 2 and d 3. ) two fifths of the area a

Example 2 pg. 6 Write Algebraic Expressions •

Example 3 pg. 6 Write an expression Mr. Nehru bought two adult tickets and three student tickets for the planetarium show. Write an algebraic expression that represents the cost of the tickets

Example 3 pg. 6 Write an expression •

1 -1 pg. 7 11 -33 o, 34 -40, 43 -61(x 3)

1 -2 Notes Algebra 1 Order of Operations

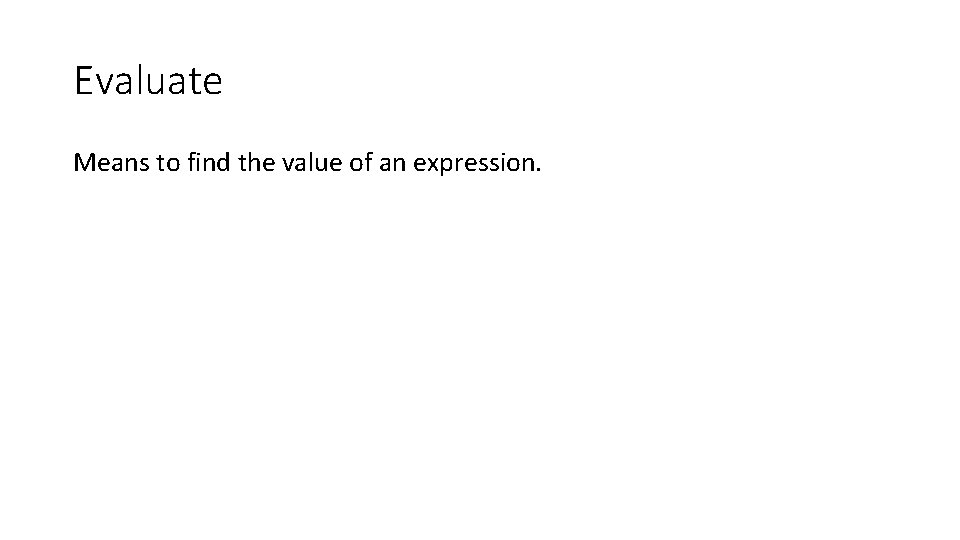
Evaluate Means to find the value of an expression.

Example 1 pg. 10 Evaluate Expressions •

Order of Operations (PEMDAS) When there is more than one operation in an expression this tells you which operation to do first. P—Parenthesis (Evaluate expressions inside grouping symbols. ) E—Exponents (Evaluate all Powers) MD—Multiply and/or Divide from left to right. AS—Add and/or Subtract from left to right.

Example 2 pg. 10 Order of Operations •

Example 3 pg. 11 Expressions with Grouping Symbols •

Example 4 pg. 11 Evaluate an Algebraic Expression •

Example 5 pg. 12 Write and Evaluate an Expression Architecture: Each side of the Great Pyramid of Giza, Egypt, is a triangle. The base of each triangle once measured 230 meters. The height of each triangle once measured 187 meters. The area of a triangle is one-half the product of the base b and its height h. a. ) Write an expression that represent the area of one side of the Great Pyramid. b. ) Find the area of one side of the Great Pyramid.

Example 5 pg. 12 Write and Evaluate an Expression •

1 -2 pg. 13 15 -35 o, 36 -38, 39 -53 o, 66 -81(x 3)

Notes for Algebra 1 Chapter 1

1 -1 Notes Algebra 1 Variables and Expressions

Algebraic Expression Consist of variables, numbers and operations.

Variables Symbols or letters used to represent unspecified numbers and values.

Term May be a number or variable or a product or quotient of numbers and variables.

Factors The quantities being multiplied in a multiplication expression

Product The answer to a multiplication expression

Exponent (power) Indicates the number of times the base is used as a factor.

Base The number that is used as a factor in an exponential expression

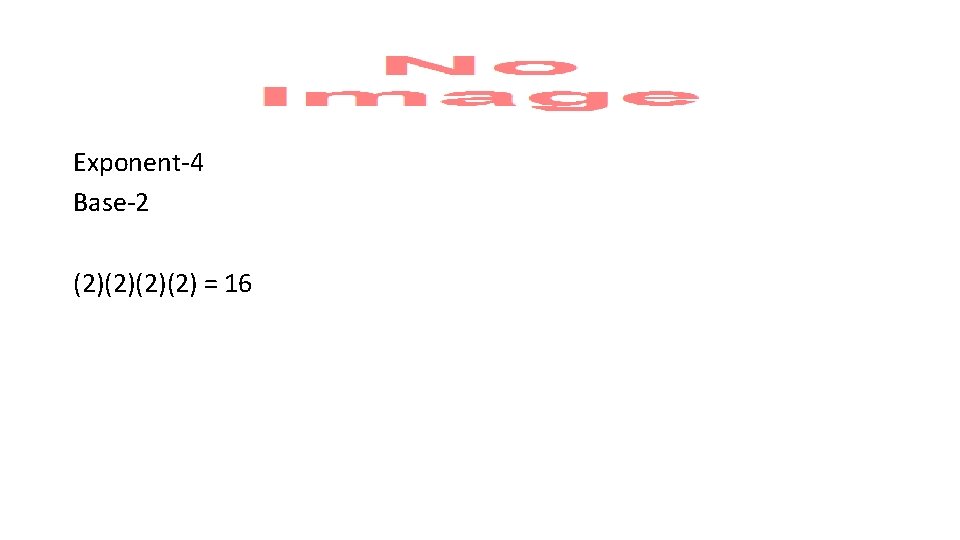
Exponent-4 Base-2 (2)(2) = 16

Example 1 pg. 5 Write a verbal expression •

Example 2 pg. 6 Write Algebraic Expressions Write an algebraic expression for each verbal expression. 1. ) 5 less than a number c 2. ) 9 plus the product of 2 and d 3. ) two fifths of the area a

Example 2 pg. 6 Write Algebraic Expressions •

Example 3 pg. 6 Write an expression Mr. Nehru bought two adult tickets and three student tickets for the planetarium show. Write an algebraic expression that represents the cost of the tickets

Example 3 pg. 6 Write an expression •

1 -1 pg. 7 11 -33 o, 34 -40, 43 -61(x 3)

1 -2 Notes Algebra 1 Order of Operations

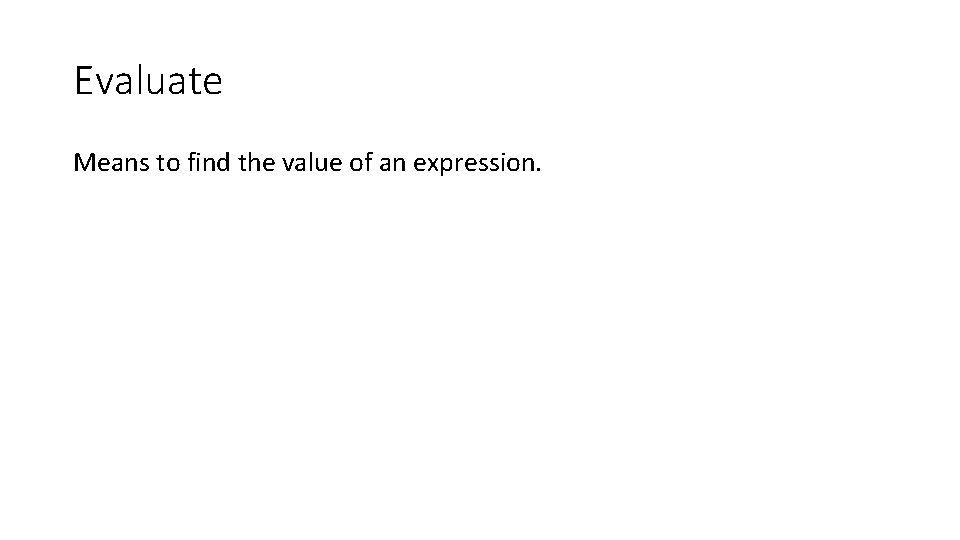
Evaluate Means to find the value of an expression.

Example 1 pg. 10 Evaluate Expressions •

Order of Operations (PEMDAS) When there is more than one operation in an expression this tells you which operation to do first. P—Parenthesis (Evaluate expressions inside grouping symbols. ) E—Exponents (Evaluate all Powers) MD—Multiply and/or Divide from left to right. AS—Add and/or Subtract from left to right.

Example 2 pg. 10 Order of Operations •

Example 3 pg. 11 Expressions with Grouping Symbols •

Example 4 pg. 11 Evaluate an Algebraic Expression •

Example 5 pg. 12 Write and Evaluate an Expression Architecture: Each side of the Great Pyramid of Giza, Egypt, is a triangle. The base of each triangle once measured 230 meters. The height of each triangle once measured 187 meters. The area of a triangle is one-half the product of the base b and its height h. a. ) Write an expression that represent the area of one side of the Great Pyramid. b. ) Find the area of one side of the Great Pyramid.

Example 5 pg. 12 Write and Evaluate an Expression •

1 -2 pg. 13 15 -35 o, 36 -38, 39 -53 o, 66 -81(x 3)

1 -4 Notes for Algebra 1 The Distributive Property

Distributive Property •

Example 1 pg. 26 Real World FITNESS Julio walks 5 days a week. He walks at a fast rate for 7 minutes and cools down for 2 minutes. Use the distributive property to write and evaluate an expression that determines the total number of minutes Julio walks.

Example 1 pg. 26 Real World •

Example 2 pg. 26 Mental Math •

Example 3 pg. 27 Algebraic Expressions •

Example 4 pg. 27 Combine like terms •

Example 5 pg. 28 Write and Simplify Expressions Use the expression six times the sum of x and y increased by four times the difference of 5 x and y. 1. ) Write an algebraic expression for the verbal expression. 2. ) Simplify the expression and indicate the properties used.

Example 5 pg. 28 Write and Simplify Expressions •

1 -4 pg. 29 11 -47 o, 48, 60 -75(x 3)

1 -5 Notes for Algebra 1 Equations

Open Sentence A mathematical statement that contains algebraic expressions and symbols

Equation A sentence that contains an equal sign.

Solving/Solution Finding a value for a variable that makes a sentence true is called solving the open sentence. This replacement value is called the solution.

Replacement Set A set of numbers from which replacements for a variable may be chosen.

Set/Element A set is a collection of objects or numbers that is often shown using braces. Each object or number in the set is called an element.

Solution set The set of elements form the replacement set that make an open sentence true.

Example 1 pg. 33 Use a replacement set •

Example 2 pg. 34 Apply the order of Operations •

Example 3 pg. 34 Solutions of Equations •

Identity An equation that is true for every value of the variable.

Example 4 pg. 35 Identities •

Example 5 pg. 35 Equations involving twovariables GYM MEMBERSHIP Dalila pays $16 per month for a gym membership. In addition, she pays $2 per Pilates class. Write and solve an equation to find the total amount Dalila spent this month if she took 12 Pilates classes.

Example 5 pg. 35 Equations involving twovariables •

1 -5 pg. 36 12 -60(x 3), 72 -90(x 3)

1 -6 Notes for Algebra 1 Relations

Coordinate System Is formed by the intersection of two number lines, the horizontal axis (x -axis) and the vertical axis (y-axis)

Ordered Pairs •

Relation A set of ordered pairs. A relation can be represented in several different ways: as an equation, in a graph, with a table, or with a mapping.

Mapping Illustrates how each element of the domain (x-coordinate) is paired with an element in the range (y-coordinate)

Example 1 pg. 41 Representations of a Relation •

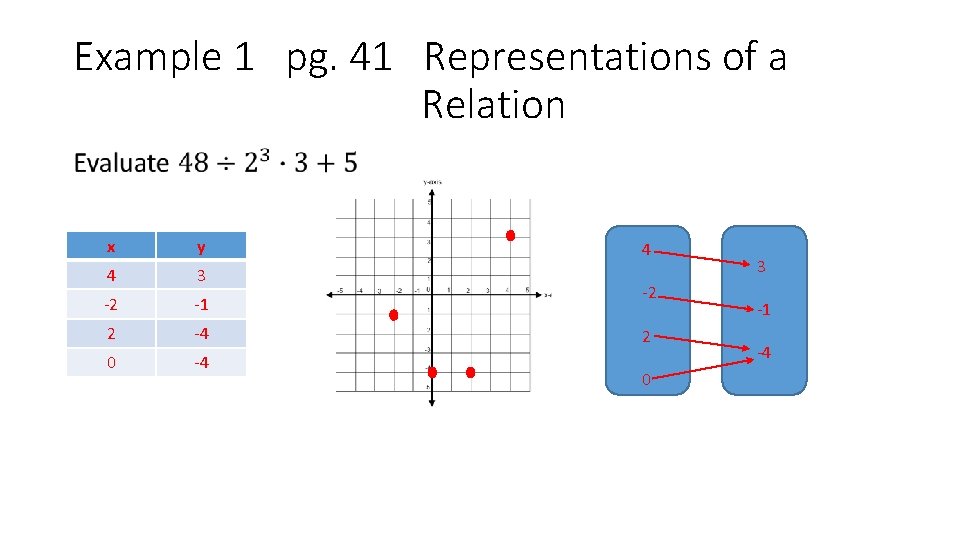
Example 1 pg. 41 Representations of a Relation • x y 4 3 -2 -1 2 -4 0 -4 4 -2 2 0 3 -1 -4

Example 2 pg. 42 Real World 1. ) CLIMATE In warm climates, the average amount of electricity used rises as the daily average temperature increases and falls as the daily average temperature decreases. 2. ) CALORIES The number of calories you burn increases as the number of minutes that you walk increases.

Example 2 pg. 42 Real World 1. ) CLIMATE In warm climates, the average amount of electricity used rises as the daily average temperature increases and falls as the daily average temperature decreases. Independent variable: temperature; dependent variable: amount of electricity used 2. ) CALORIES The number of calories you burn increases as the number of minutes that you walk increases. Independent variable: time; dependent variable: number of calories burned

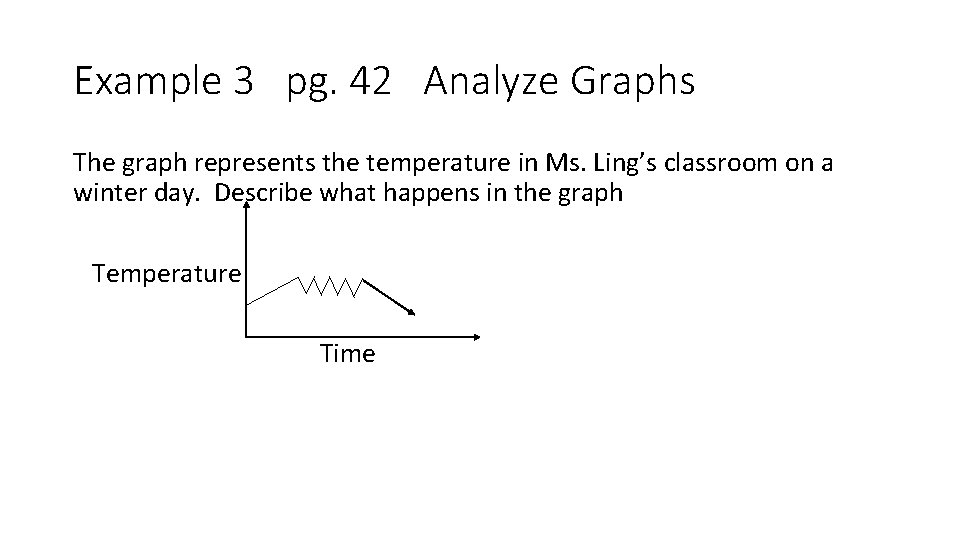
Example 3 pg. 42 Analyze Graphs The graph represents the temperature in Ms. Ling’s classroom on a winter day. Describe what happens in the graph Temperature Time

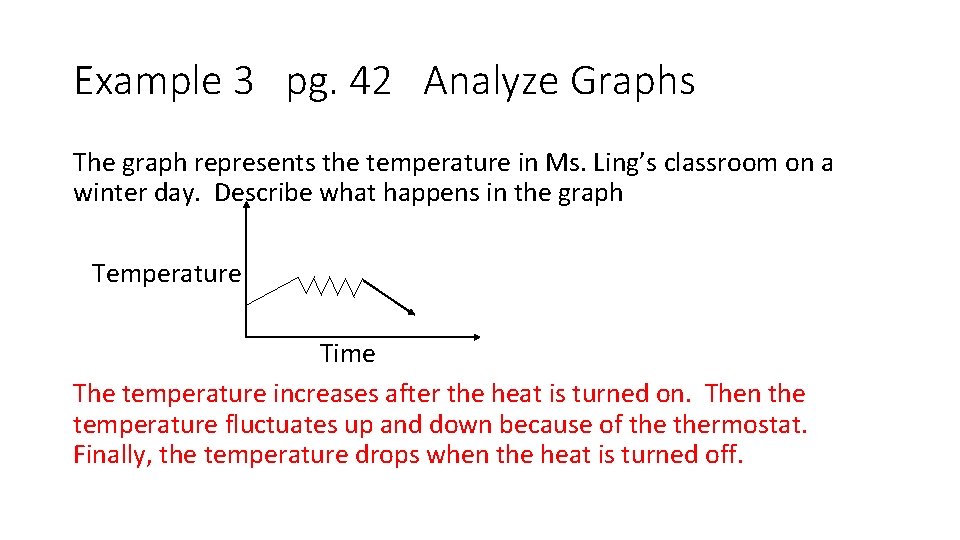
Example 3 pg. 42 Analyze Graphs The graph represents the temperature in Ms. Ling’s classroom on a winter day. Describe what happens in the graph Temperature Time The temperature increases after the heat is turned on. Then the temperature fluctuates up and down because of thermostat. Finally, the temperature drops when the heat is turned off.

1 -6 pg. 40 9 -31 o, 45 -60(x 3)

1 -7 Notes for Algebra 1 Functions

Function A relationship between the input (domain, x) and output (range, y). In a function, there is exactly one output for each input.

Example 1 pg. 47 Identify Functions • Domain Range -7 -12 -4 -9 2 3 5 0

Example 2 pg. 49 Equations as Functions SCHOOL CAFETERIA there are 3 lunch periods at a school. During the 1 st period, 352 students eat. During the 2 nd period, 304 students eat. During the 3 rd period, 391 students eat. 1. ) Make a table showing the number of students for each of the 3 lunch periods. 2. ) Determine the domain and range of the function. 3. ) Write the data as a set of ordered pairs. Then graph the data. 4. ) State whether the function is discrete or continuous. Explain your reasoning.

Example 2 pg. 49 Equations as Functions SCHOOL CAFETERIA there are 3 lunch periods at a school. During the 1 st period, 352 students eat. During the 2 nd period, 304 students eat. During the 3 rd period, 391 students eat. 1. ) Make a table showing the number of students for each of the 3 lunch periods. Period 1 2 3 Number of Students 352 304 391

Example 2 pg. 49 Equations as Functions •

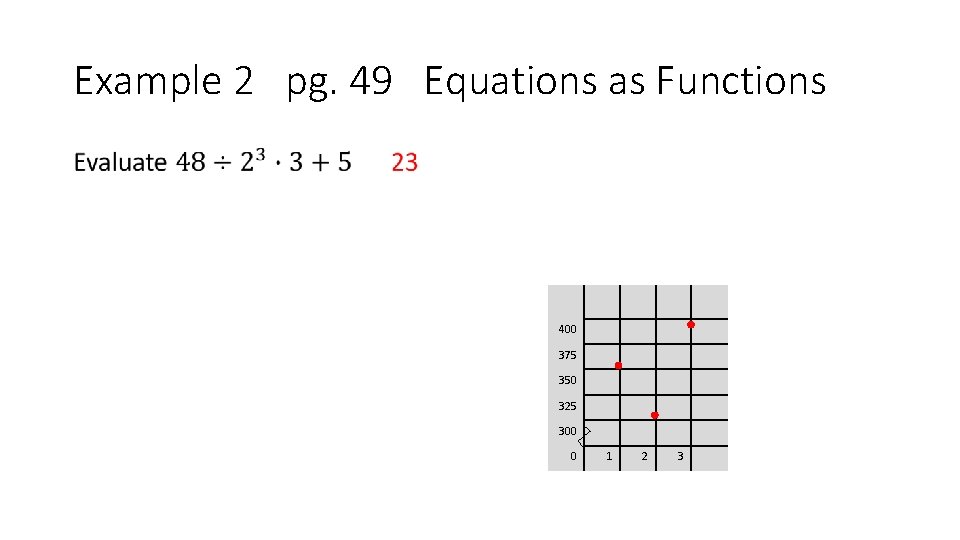
Example 2 pg. 49 Equations as Functions • 400 375 350 325 300 0 1 2 3

Example 2 pg. 49 Equations as Functions SCHOOL CAFETERIA there are 3 lunch periods at a school. During the 1 st period, 352 students eat. During the 2 nd period, 304 students eat. During the 3 rd period, 391 students eat. 4. ) State whether the function is discrete or continuous. Explain your reasoning. Because the points are not connected, the function is discrete.

Example 3 pg. 49 Representation of a Function Determine whether x = -2 represents a function.

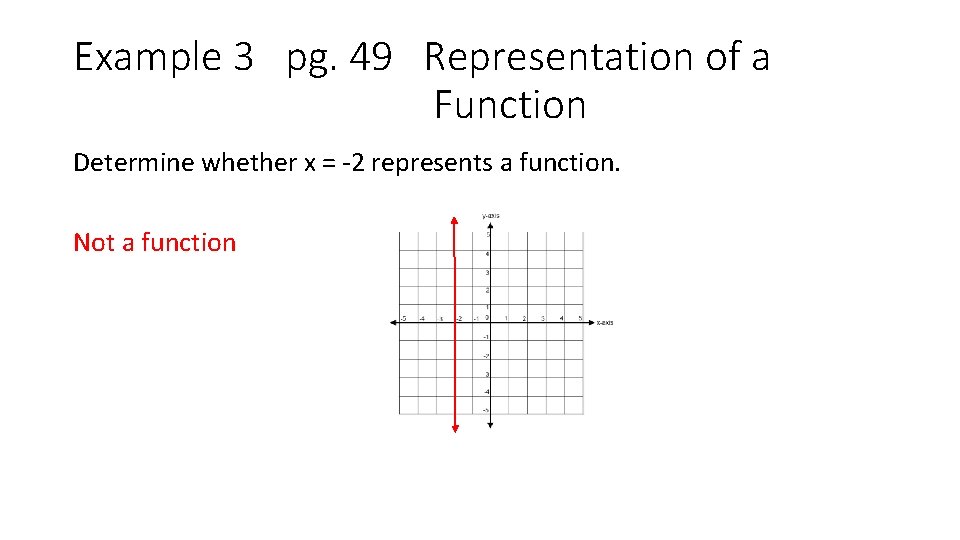
Example 3 pg. 49 Representation of a Function Determine whether x = -2 represents a function. Not a function

Example 4 pg. 50 Function Values •

Example 5 pg. 50 Nonlinear Function Values •

1 -7 pg. 52 21 -47 o, 57 -75(x 3)

1 -8 Notes for Algebra 1 Interpreting Graphs of Functions

Intercepts Are points on the graph where it intersects an axis. x-intercept crosses the x-axis y-intercept crosses the y-axis.

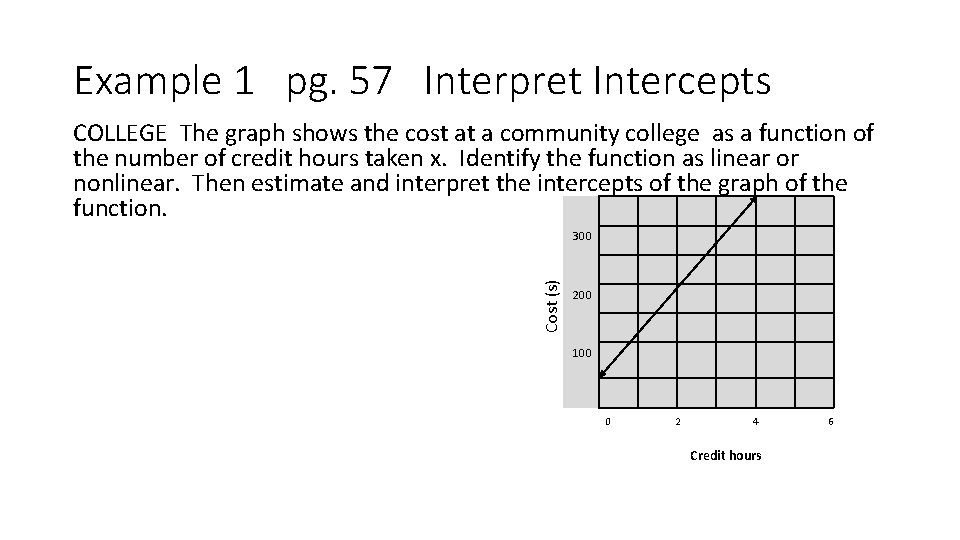
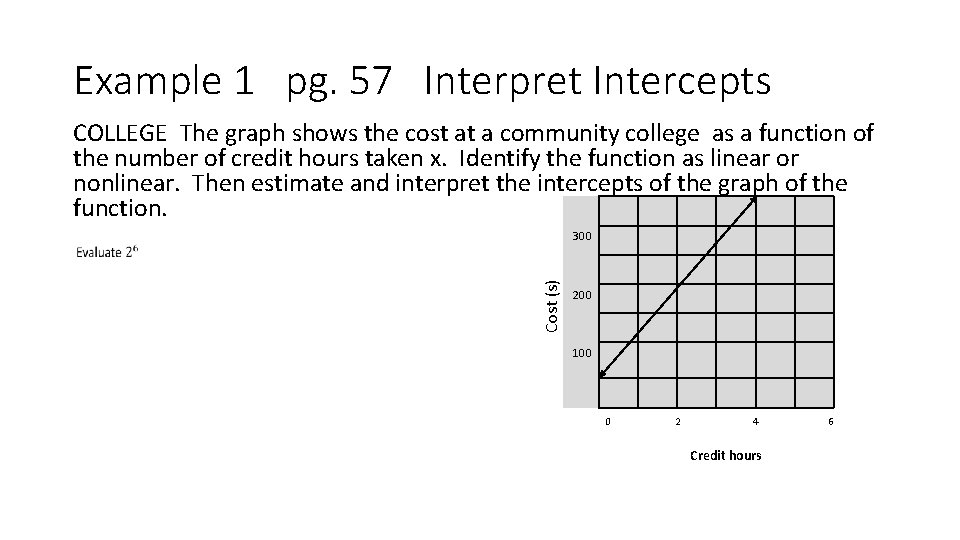
Example 1 pg. 57 Interpret Intercepts COLLEGE The graph shows the cost at a community college as a function of the number of credit hours taken x. Identify the function as linear or nonlinear. Then estimate and interpret the intercepts of the graph of the function. Cost (s) 300 200 100 0 2 4 Credit hours 6

Example 2 pg. 57 Real World MANUFACTURING The graph shows the cost y to manufacture x units of product. Describe and interpret any symmetry. Manufacturing Cost(s) Manufacturing Costs 800 400 0 20 40 Number of Units

Example 2 pg. 57 Real World MANUFACTURING The graph shows the cost y to manufacture x units of product. Describe and interpret any symmetry. The right half of the graph is the mirror Image of the left half in approximately the Line x = 30. The symmetry of the graph Tells you that the cost to produce n more or n less than 30 units will be the same. Manufacturing Cost(s) Manufacturing Costs 800 400 0 20 40 Number of Units

Example 3 pg. 58 Real World Deer population Number of Deer DEER The graph show the population y of deer x years after the animals are introduced on an island. Estimate and interpret where the function is positive, negative, increasing, and decreasing, the x-coordinates of any relative extrema, and the end behavior of the graph. 120 80 40 0 2 4 Time (years) 6

Example 3 pg. 58 Real World Deer population Number of Deer Nonlinear; the y-intercept is about 75, Indicating an initial population of 75 deer. The x-intercept of about 5. 6 indicates that the population died about 5. 6 years after the deer were introduced to the island. The graph has no line symmetry. The population decreased the first year, increased between year 1 and 4, and then decreased to 0 after year 4. The population experienced a relative low at the end of year 1 and a relative high at the end of year 4. As the years passed, The population decreased to 0. 120 80 40 0 2 4 Time (years) 6

1 -8 pg. 59 5 -9 o, 24 -36 (x 3)