Notes Dijstras Algorithm Corrected syllabus Tree Search Implementation

Notes Dijstra’s Algorithm Corrected syllabus

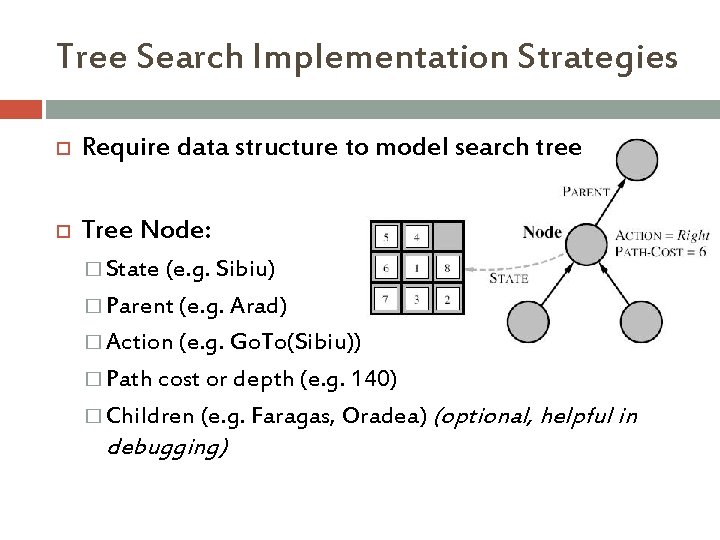
Tree Search Implementation Strategies Require data structure to model search tree Tree Node: � State (e. g. Sibiu) � Parent (e. g. Arad) � Action (e. g. Go. To(Sibiu)) � Path cost or depth (e. g. 140) � Children (e. g. Faragas, Oradea) (optional, helpful in debugging)

Queue Methods: � Empty(queue) Returns true if there are no more elements � Pop(queue) Remove and return the first element � Insert(queue, element) Inserts element into the queue Insert. FIFO(queue, element) – inserts at the end Insert. LIFO(queue, element) – inserts at the front Insert. Priority(queue, element, value) – inserts sorted by value

INFORMED SEARCH

Search start goal Uninformed search Informed search

Informed Search What if we had an evaluation function h(n) that gave us an estimate of the cost associated with getting from n to the goal � h(n) is called a heuristic

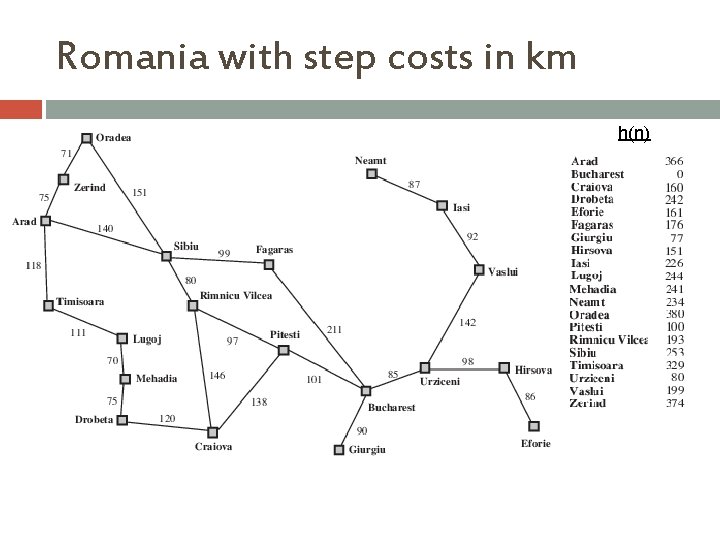
Romania with step costs in km h(n)

Greedy best-first search Evaluation function f(n) = h(n) (heuristic) � e. g. , f(n) = h. SLD(n) = straight-line distance from n to Bucharest Greedy best-first search expands the node that is estimated to be closest to goal

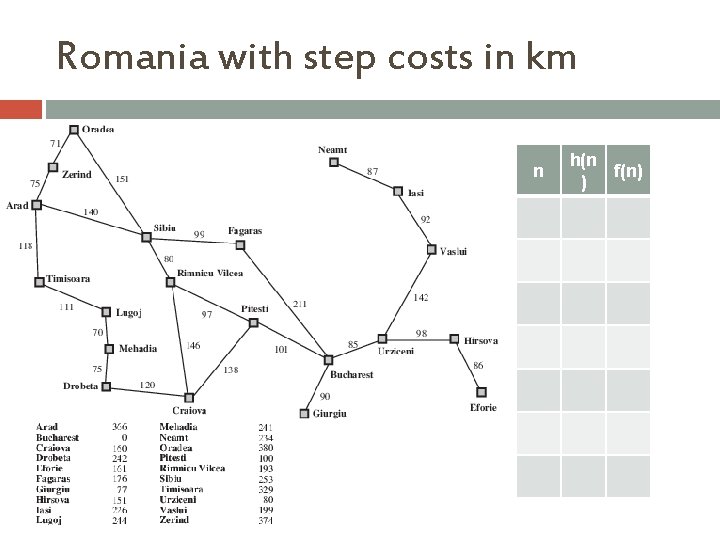
Romania with step costs in km n h(n f(n) )

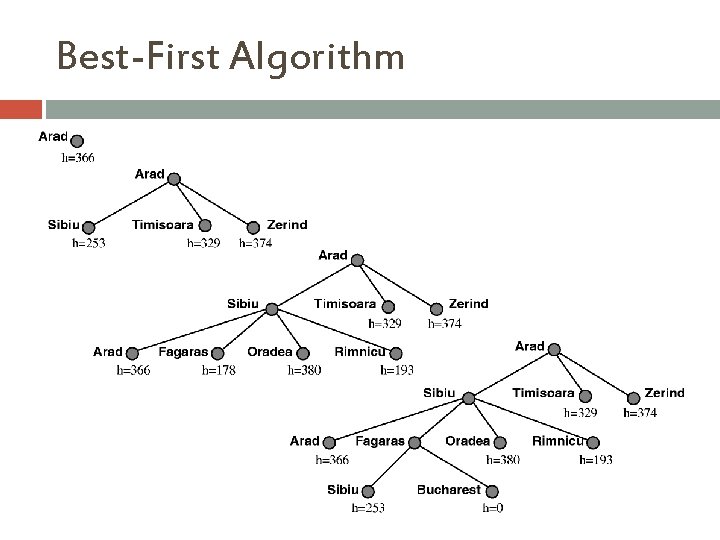
Best-First Algorithm

Performance of greedy best-first search Complete? Optimal?

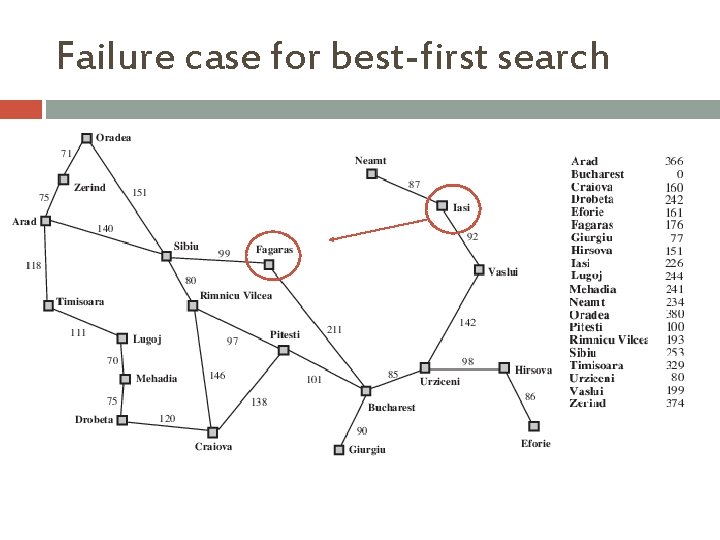
Failure case for best-first search

Performance of greedy best-first search Complete? � No – can get stuck in loops, e. g. , Iasi Neamt Optimal? � No Neamt Iasi

Complexity of greedy best first search Time? � O(bm), but a good heuristic can give dramatic improvement Space? � O(bm) -- keeps all nodes in memory

What can we do better?

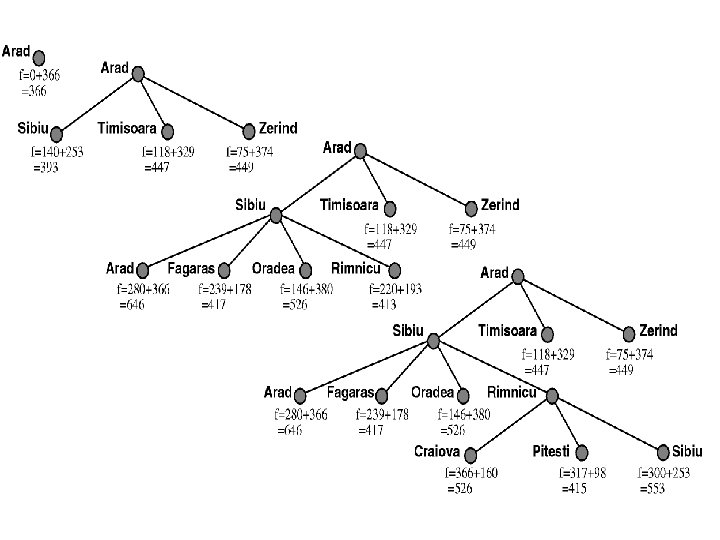
* A search Ideas: � Avoid expanding paths that are already expensive � Consider Cost to get here (known) – g(n) Cost to get to goal (estimate from the heuristic) – h(n)

A * Evaluation functions Evaluation function f(n) = g(n) + h(n) � g(n) = cost so far to reach n � h(n) = estimated cost from n to goal � f(n) = estimated total cost of path through n to goal n start g(n) h(n) f(n)

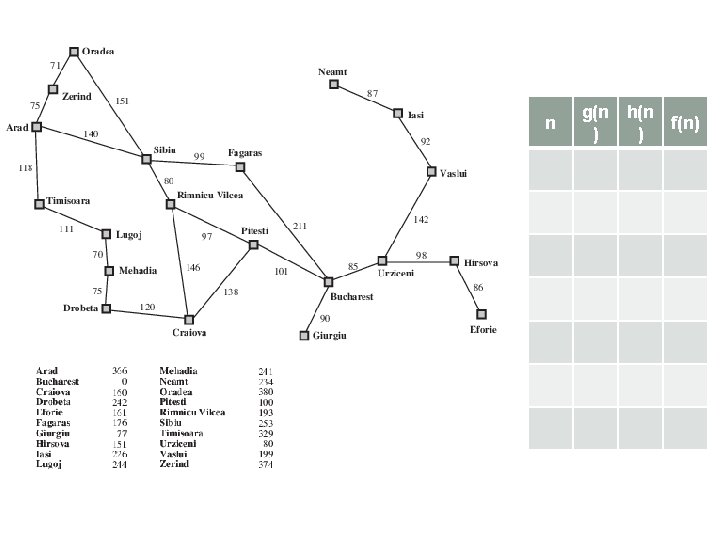
n g(n h(n f(n) ) )

A* Heuristics A heuristic h(n) is admissible if for every node n, h(n) ≤ h*(n), where h*(n) is the true cost to reach the goal state from n. An admissible heuristic never overestimates the cost to reach the goal, i. e. , it is optimistic � Example: h. SLD(n) (never overestimates the actual road distance)

What happens if heuristic is not admissible? Will still find solution (complete) But might not find best solution (not optimal)

Properties of A* (w/ admissible heuristic) Complete? � Optimal? � Yes Time? � Yes (unless there are infinitely many nodes with f ≤ f(G) ) Exponential, approximately O(bd) in the worst case Space? � O(bm) Keeps all nodes in memory

The heuristic h(x) guides the performance of A* Let d(x) be the actual distance between S and G � h(x) = 0 : A* is equivalent to Uniform-Cost Search � h(x) <= d (x) : guarantee to compute the shortest path; the lower the value h(x), the more node A* expands � h(x) = d (x) : follow the best path; never expand anything else; difficult to compute h(x) in this way! � h(x) > d(x) : not guarantee to compute a best path; but very fast � h(x) >> g(x) : h(n) dominates -> A* becomes the best first search

Admissible heuristics

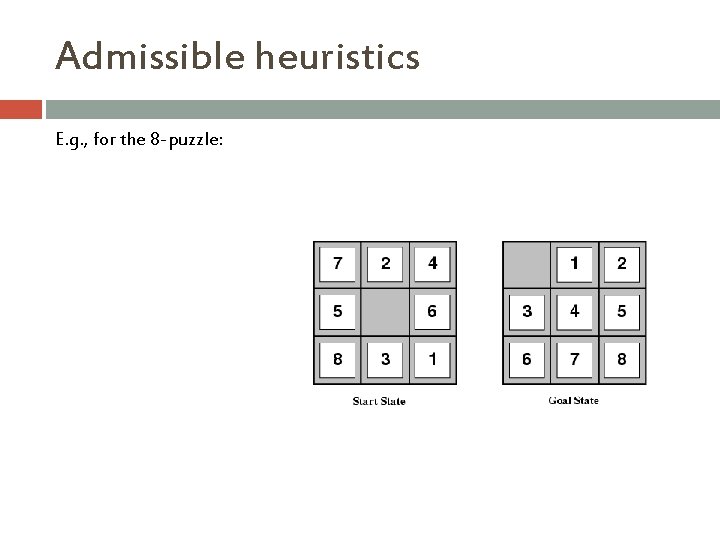
Admissible heuristics E. g. , for the 8 -puzzle:

Admissible heuristics E. g. , for the 8 -puzzle: h 1(n) = number of misplaced tiles h 2(n) = summed Manhattan distance for all tiles (i. e. , no. of squares from desired location of each tile) h 1(S) = ? h 2(S) = ?

Admissible heuristics E. g. , for the 8 -puzzle: h 1(n) = number of misplaced tiles h 2(n) = total Manhattan distance (i. e. , no. of squares from desired location of each tile) h 1(S) = ? 8 h 2(S) = ? 3+1+2+2+2+3+3+2 = 18 Which is better?

Dominance If h 2(n) ≥ h 1(n) for all n (both admissible) � then h 2 dominates h 1 � h 2 is better for search What does better mean? � All searches we’ve discussed are exponential in time

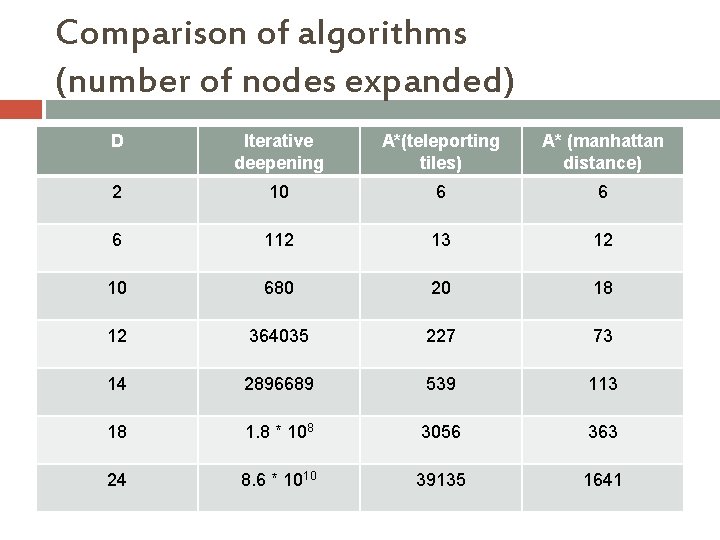
Comparison of algorithms (number of nodes expanded) D Iterative deepening A*(teleporting tiles) A* (manhattan distance) 2 10 6 6 6 112 13 12 10 680 20 18 12 364035 227 73 14 2896689 539 113 18 1. 8 * 108 3056 363 24 8. 6 * 1010 39135 1641

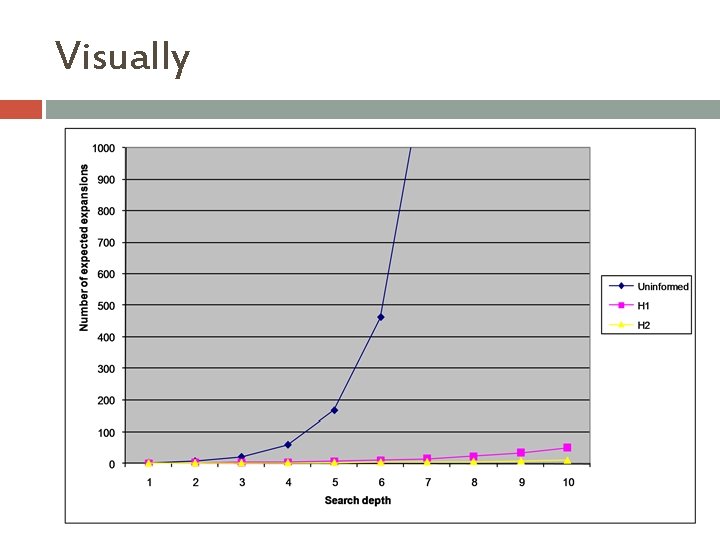
Visually

Where do heuristics come from? From people � Knowledge of the problem From computers � By considering a simpler version of the problem � Called a relaxation

Relaxed problems 8 -puzzle � If the rules of the 8 -puzzle are relaxed so that a tile can move anywhere, then h 1(n) gives the shortest solution � If the rules are relaxed so that a tile can move to any adjacent square, then h 2(n) gives the shortest solution Consider the example of straight line distance (Romania navigation) � Is that a relaxation?

Iterative-Deepening A* (IDA*) Further reduce memory requirements of A* Regular Iterative-Deepening: regulated by depth IDA*: regulated by f(n)=g(n)+h(n)

Questions?