Notes A Different exam boards Sampling type AQA

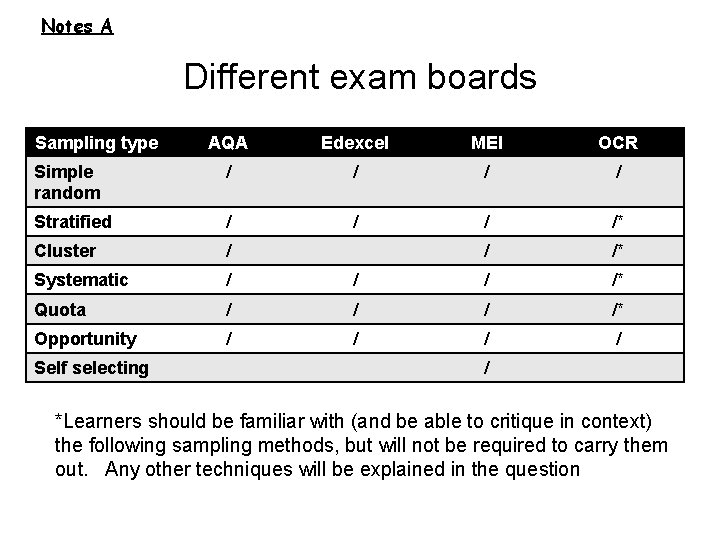
Notes A Different exam boards Sampling type AQA Edexcel MEI OCR Simple random / / Stratified / /* Cluster / / /* Systematic / /* Quota / /* Opportunity / / Self selecting / *Learners should be familiar with (and be able to critique in context) the following sampling methods, but will not be required to carry them out. Any other techniques will be explained in the question

Sampling • KUS objectives BAT explore sampling methods and know their strengths and weaknesses Starter: Tell your partner what you think these terms mean Representative Exit Poll Census

WB 1 Sampling Why do we need to sample? What makes a good sample? Desmos activity for this lesson

WB 1 Population How would you define a population? A population includes every data value that fits the definition of the population.

WB 1 A Census A census is an investigation of a complete population. In the UK the government carries out a census of the population every 10 years – the last one was in 2011. Click for 2011 Census catalogue

WB 1 Populations • Populations are – Finite – Infinite – Either § Explain your answer

WB 1 Populations

WB 1 Sampling Frame In order to select a random sample you need a list of all the members of the population. This is called a sampling frame. For example, a Sampling frame for a school could be a database of all the students. Each individual student would then be a sampling unit.

WB 1 Sampling terminology Pair up each statement with the correct example Sampling is an important Mathematical tool used in a wide range of fields, from piloting new drugs to testing electrical & mechanical parts to marketing. Eg if the Head wished to survey pupils, A population is a collection of all items (of a group) All pupils attending the school A sampling unit is an individual member of a population A census is when all members of a population are polled. A census gives reliable information but is time consuming, expensive, and impossible if testing destroys sample (e. g. testing product lifespan). Surveying every pupil The pupils A sample survey is when only part of a population is polled. A sampling frame is a potential source of sample units. A sample is cheaper & quicker but potentially not representative and biased. A full list of pupils Surveying a selection of pupils

WB 2 Sampling What do you understand by the following terms? a) b) c) Simple random sample Representative sample Bias A sample is a number of data values from within a population, which can be used to find out more about a population in situations where it is impractical to study the whole population (perhaps because it is too large). Samples can be chosen in a number of ways. In further work we will assume that all samples are random (i. e. the individuals in the sample were chosen randomly from the population). In practice, samples are not always random, sometimes because of practical difficulties, or because it might be desirable to use a sample constructed in a different way (e. g. in a survey involving people, you might wish to use an equal number of men and women). A good sample is unbiased, i. e. it is representative of the population.

WB 2 Simple Random Sampling A simple random sample of size n is a sample chosen in such a way that each possible group of size n which could be taken from the population has the same chance of being picked. “A simple random sample will be representative of the population". . A slightly better explanation is “Simple random sampling eliminates bias by giving all samples an equal chance to be chosen. “ The real reason: The mathematical theorems which justify most frequently used statistical procedures apply only to random samples

WB 2 Bias A sampling method is called biased if it systematically favours some outcomes over others. Bias can be intentional, but often it is not. An example is ‘telephone polling ’ - a sample can be biased, even though there is some randomness in the selection of the sample. Inferences from a biased sample are not as trustworthy as conclusions from a truly random sample.

WB 2 Sample bias- an example A well reported landline telephone poll before the 2015 election predicted that the results would be similar to previously. In fact the SNP gained 50 seats and Labour lost 40 seats Where did they go wrong?

Lets do some Sampling

You are given 100 natural numbers, all less than 100. Your task is to estimate the mean by taking a sample.

WB 3 A representative sample Have a good look at the 100 numbers Select what you consider to be a representative sample of 20 numbers - using nothing but intuition! (choose the numbers yourself by eye) Work out the mean of your representative sample

WB 4 A Random number generator Calculator or spreadsheet random three-digit numbers between 0 and 1. 000 Classwhiz Type: Alpha Internet For example https: //www. random. org/integers/ Low tech Names out a hat or using a table of random numbers Type 100 x Shift ● ● Ran. Int(1, 100) But how do we know all of these are truly random? Can you find a problem with each of these

WB 4 A simple random sample The same 100 numbers. Imagine them numbered 1 to 100. This would be the 36 th Use a random number generator to take a simple random sample of size 20. Repeats are allowed. Work out the mean of your a simple random sample

WB 4 A random sample – example 0. 898 0. 032 0. 74 0. 006 0. 53 0. 068 0. 64 0. 989 0. 962 0. 501 0. 207 0. 280 0. 299 0. 413 0. 454 0. 869 0. 664 0. 381 0. 489 0. 245

WB 5 1 2 Stratified Random Sampling 3 4 5 7 8 9 10 11 12 13 14 15 16 17 18 6 In a stratified random sample we take a proportion of each group For example 10% of each year group in a school

WB 5 A Stratified sample The same 100 numbers. Imagine they are in four distinct groups. Take a stratified random sample of size 20. Work out the mean of your a simple random sample

WB 6 Systematic Sampling

WB 6 Systematic Sampling Advantages: • It is relatively straight-forward to set up • A good ‘coverage’ of the population can be more easily achieved than using random sampling Disadvantages: • It is potentially more biased, as not all members or points have an equal chance of being selected • It may therefore lead to over or under representation of a particular pattern • Need a sampling frame

WB 6 A Systematic sample Select a starting point randomly (from …? ) Select a systematic sample of size 20 Work out the mean of your systematic sample

WB 7 Quota Sampling • This similar to stratified sampling in that certain subgroups of the population are identified and a ‘quota’ of each sub-group is required for the sample. • However rather than then select randomly or systematically, data items are taken in order from the sampling frame until each quota is full.

WB 7 Quota Sampling Advantages: • Don’t need access to the whole sampling frame • Quick and relatively cheap to administer • Can give a flavour of trends across different groups Disadvantages: • Difficult to quantify any sampling errors, so don’t know if it is biased • Not based on random methods, so further work limited • Quotas may not be accurate

WB 7 A Quota sample We need a method for choosing the sample Select a quota sample of size 20: Starting with the first data item, select 7 items less than 15, 7 items between 15 and 35, 6 items over 35. Work out the mean of your systematic sample (you will find you can only pick 18 for your sample – why is this? )

WB 8 Cluster Sampling Sometimes a sampling frame is not easily available. Instead it is easier to identify clusters of units. For residents of a country, clusters might be counties For students, clusters might be schools For elderly people, clusters might be nursing homes Instead of randomly selecting the units, we randomly select the clusters and use all sampling units within that cluster. If you wanted to interview 1% of the families in a city. You could divide it up into blocks of equal population and using a map, number these blocks. Then select 1% of these blocks by simple random sampling and select every family in these blocks to interview.

WB 8 Cluster Sampling Advantages: Don’t need a whole sampling frame It is cheaper and easier to concentrate in limited clusters if these represent geographical areas Disadvantages: The clusters may have characteristics that may introduce bias

WB 8 A Cluster sample We need a the data to be in groups Select a cluster sample of size 20: i. e. two groups chosen randomly Work out the mean of your cluster sample

WB 9 Opportunity sampling The manager of a University gets a call from the Chancellor saying they need a report on the spending habits of students at the University by the end of the day. So they send someone to ask students coming out of the library that morning to fill in a questionnaire. Opportunity Sampling Uses people from target population available at the time and willing to take part. It is based on convenience. If you are sampling from a population that is very similar, then opportunity sampling may provide a sufficient estimate of the population.

WB 10 Summary Results The true mean of the 100 numbers is 11. 69. How close were we ? Which kind of sampling gives the best results?

• KUS objectives BAT explore sampling methods and know their strengths and weaknesses self-assess One thing learned is – One thing to improve is –

END