Notes 7 Knowledge Representation The Propositional Calculus ICS

Notes 7: Knowledge Representation, The Propositional Calculus ICS 271 Fall 2008

Outline z Representing knowledge using logic y Agent that reason logically y A knowledge based agent z Representing and reasoning with logic y Propositional logic x Syntax x Semantic x validity and models x Rules of inference for propositional logic x Resolution x Complexity of propositional inference. z Reading: Russel and Norvig, Chapter 7 ICS-270 A: Notes 7: 2

Knowledge bases z Knowledge base = set of sentences in a formal language z Declarative approach to building an agent (or other system): y Tell it what it needs to know z Then it can Ask itself what to do - answers should follow from the KB z Agents can be viewed at the knowledge level i. e. , what they know, regardless of how implemented z Or at the implementation level y i. e. , data structures in KB and algorithms that manipulate them ICS-270 A: Notes 7: 3

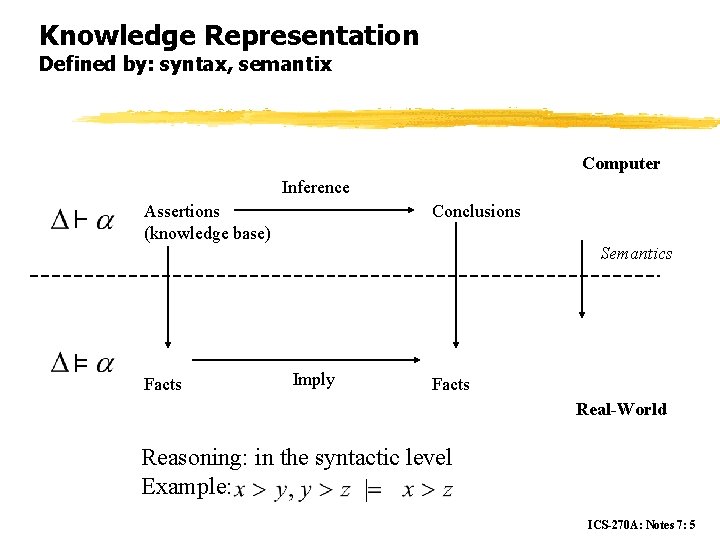
Knowledge Representation Defined by: syntax, semantix Computer Inference Assertions (knowledge base) Conclusions Semantics Facts Imply Facts Real-World Reasoning: in the syntactic level Example: ICS-270 A: Notes 7: 5

The party example z If Alex goes, then Beki goes: A B z If Chris goes, then Alex goes: C A z Beki does not go: not B z Chris goes: C z Query: Is it possible to satisfy all these conditions? z Should I go to the party? ICS-270 A: Notes 7: 6

Example of languages z Programming languages: y Formal languages, not ambiguous, but cannot express partial information. Not expressive enough. z Natural languages: y Very expressive but ambiguous: ex: small dogs and cats. z Good representation language: y Both formal and can express partial information, can accommodate inference z Main approach used in AI: Logic-based languages. ICS-270 A: Notes 7: 7

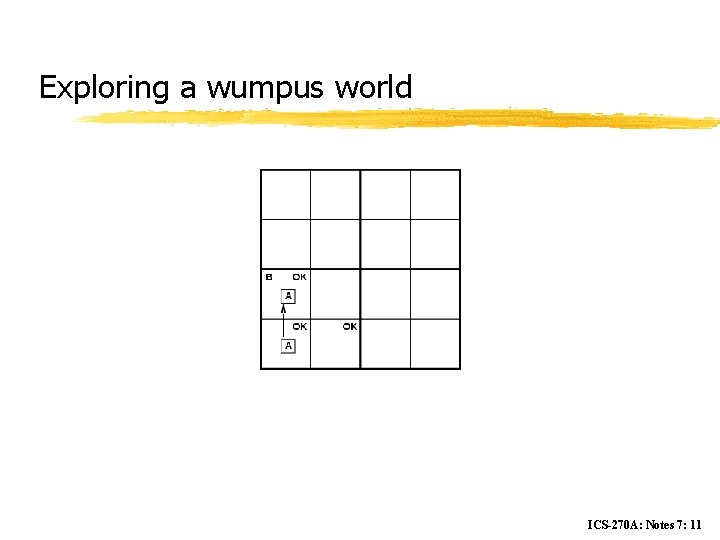
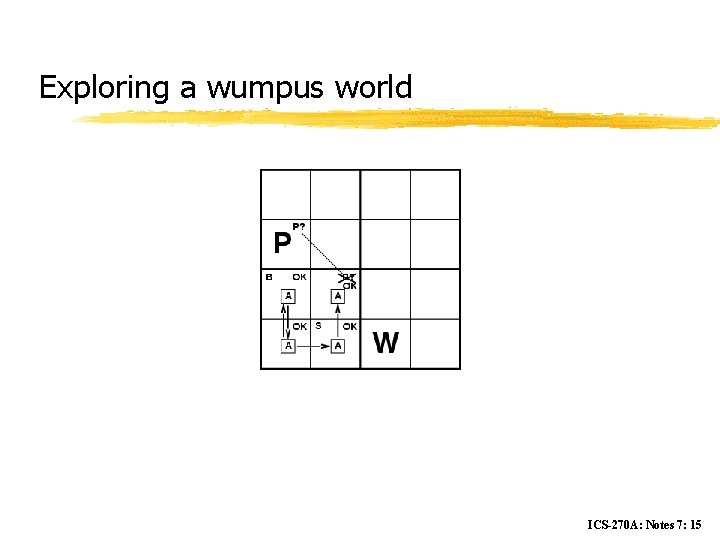
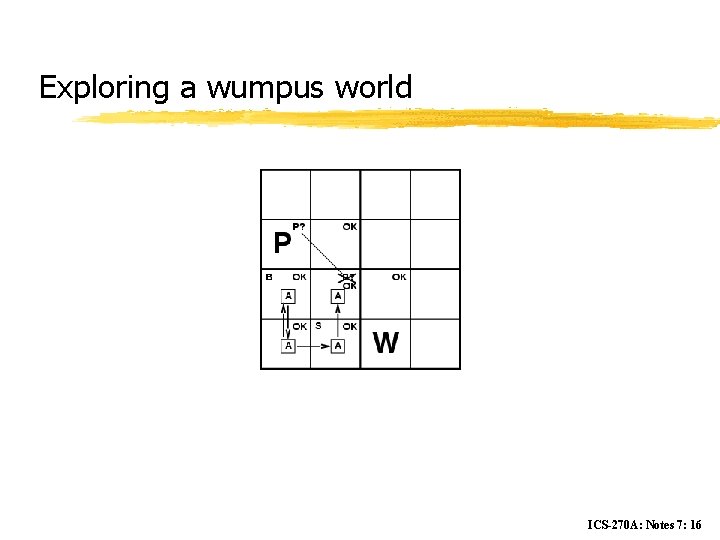
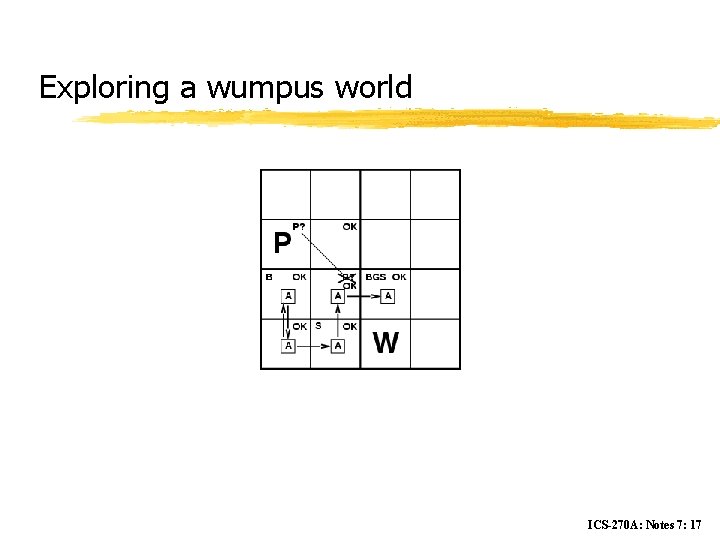
Wumpus World test-bed z Performance measure y gold +1000, death -1000 y -1 per step, -10 for using the arrow z Environment y Squares adjacent to wumpus are smelly y Squares adjacent to pit are breezy y Glitter iff gold is in the same square y Shooting kills wumpus if you are facing it y Shooting uses up the only arrow y Grabbing picks up gold if in same square y Releasing drops the gold in same square ICS-270 A: Notes 7: 8

Wumpus world characterization z Fully Observable No – only local perception z Deterministic Yes – outcomes exactly specified z Episodic No – sequential at the level of actions z Static Yes – Wumpus and Pits do not move z Discrete Yes z Single-agent? Yes – Wumpus is essentially a natural feature ICS-270 A: Notes 7: 9

Exploring a wumpus world ICS-270 A: Notes 7: 10

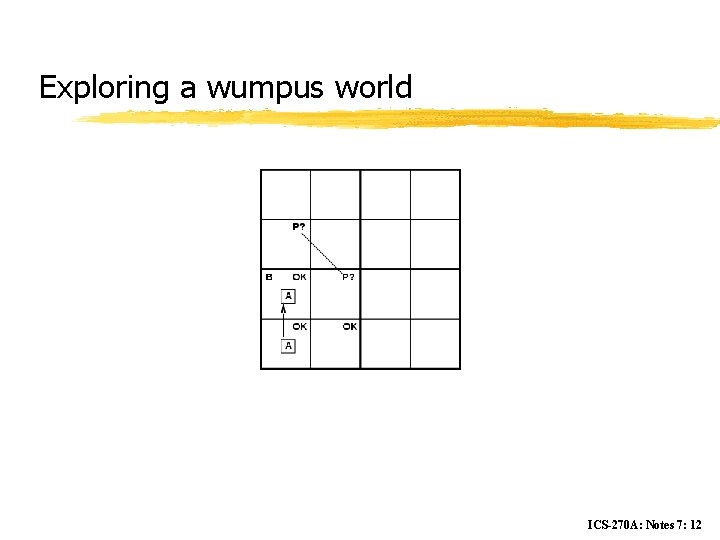
Exploring a wumpus world ICS-270 A: Notes 7: 11

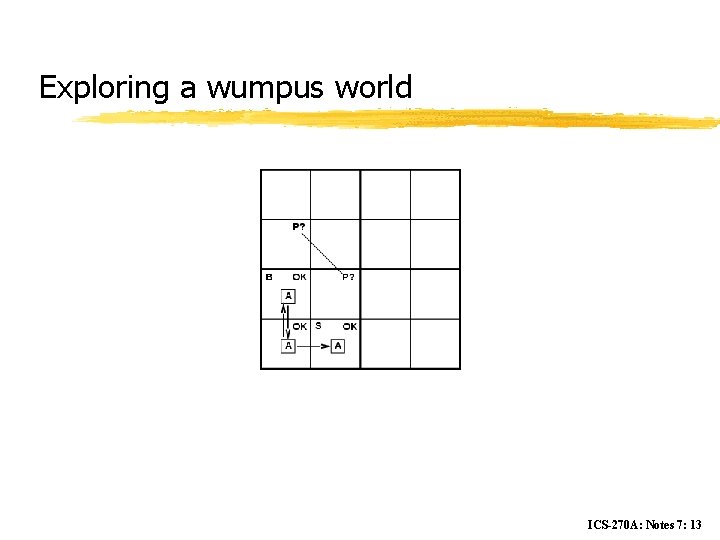
Exploring a wumpus world ICS-270 A: Notes 7: 12

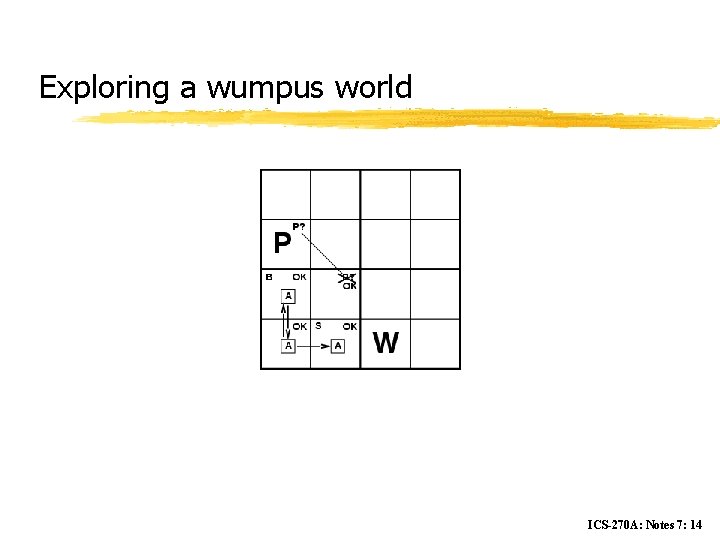
Exploring a wumpus world ICS-270 A: Notes 7: 13

Exploring a wumpus world ICS-270 A: Notes 7: 14

Exploring a wumpus world ICS-270 A: Notes 7: 15

Exploring a wumpus world ICS-270 A: Notes 7: 16

Exploring a wumpus world ICS-270 A: Notes 7: 17

Logic in general z Logics are formal languages for representing information such that conclusions can be drawn z Syntax defines the sentences in the language z Semantics define the "meaning" of sentences; y i. e. , define truth of a sentence in a world z E. g. , the language of arithmetic y x+2 ≥ y is a sentence; x 2+y > {} is not a sentence y x+2 ≥ y is true iff the number x+2 is no less than the number y ICS-270 A: Notes 7: 18

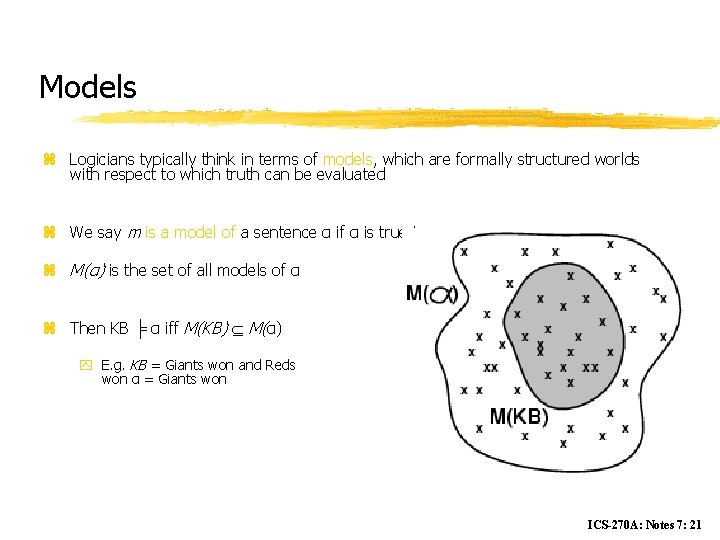
Entailment z Entailment means that one thing follows from another: KB ╞ α z Knowledge base KB entails sentence α if and only if α is true in all worlds where KB is true y E. g. , the KB containing “the Giants won” and “the Reds won” entails “Either the Giants won or the Reds won” y E. g. , x+y = 4 entails 4 = x+y y Entailment is a relationship between sentences (i. e. , syntax) that is based on semantics ICS-270 A: Notes 7: 20

Models z Logicians typically think in terms of models, which are formally structured worlds with respect to which truth can be evaluated z We say m is a model of a sentence α if α is true in m z M(α) is the set of all models of α z Then KB ╞ α iff M(KB) M(α) y E. g. KB = Giants won and Reds won α = Giants won ICS-270 A: Notes 7: 21

Entailment in the wumpus world Situation after detecting nothing in [1, 1], moving right, breeze in [2, 1] Consider possible models for KB assuming only pits 3 Boolean choices 8 possible models ICS-270 A: Notes 7: 22

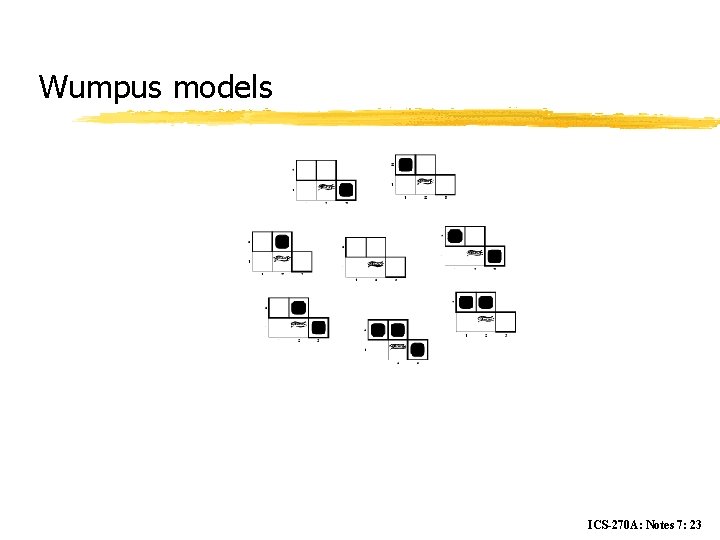
Wumpus models ICS-270 A: Notes 7: 23

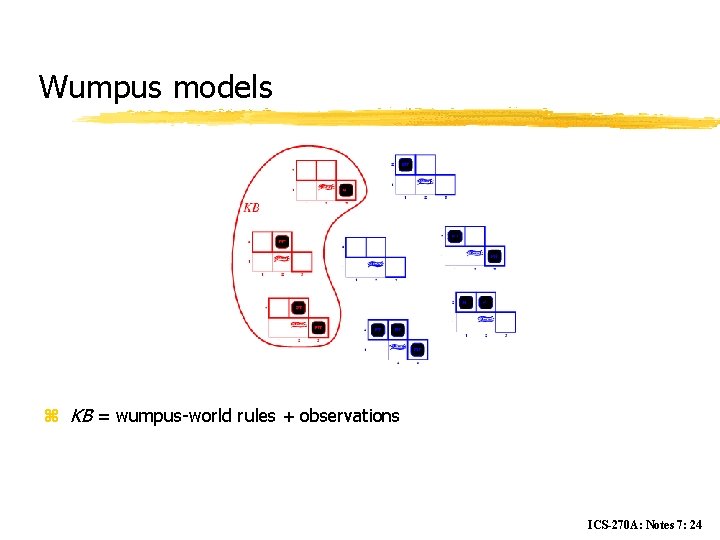
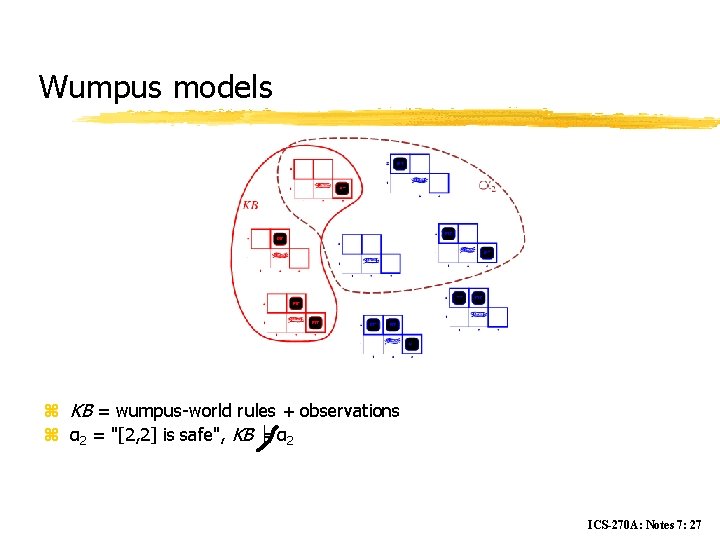
Wumpus models z KB = wumpus-world rules + observations ICS-270 A: Notes 7: 24

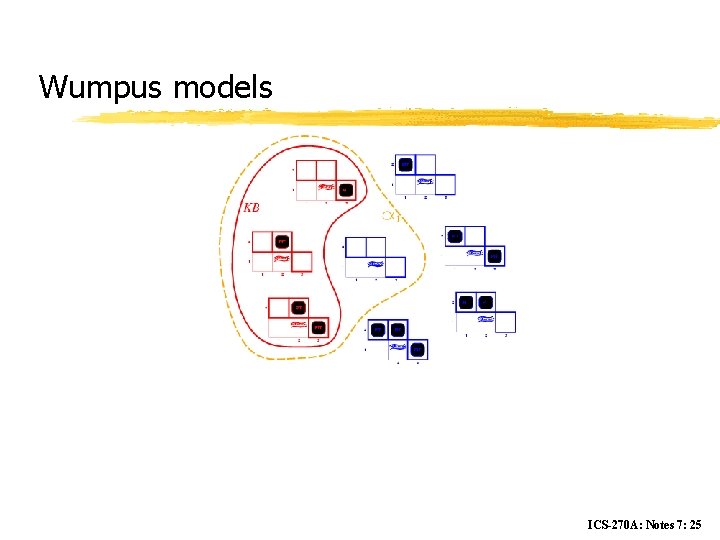
Wumpus models ICS-270 A: Notes 7: 25

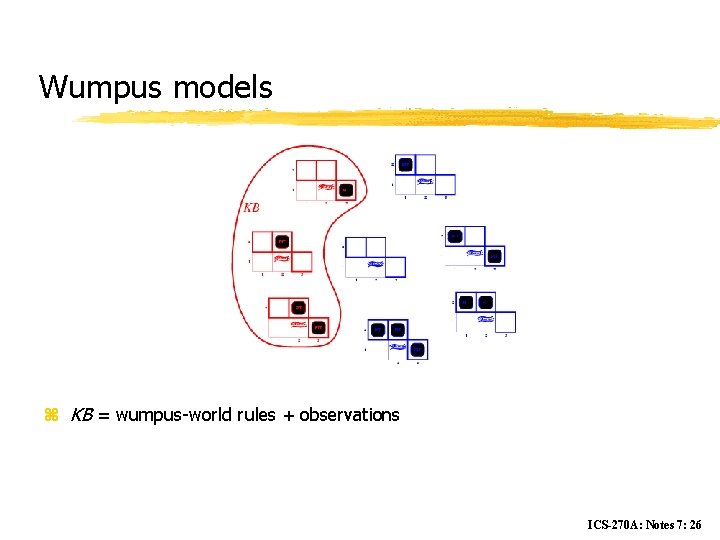
Wumpus models z KB = wumpus-world rules + observations ICS-270 A: Notes 7: 26

Wumpus models z KB = wumpus-world rules + observations z α 2 = "[2, 2] is safe", KB ╞ α 2 ICS-270 A: Notes 7: 27

ICS-270 A: Notes 7: 28

Propositional logic: Syntax z Propositional logic is the simplest logic – illustrates basic ideas z The proposition symbols P 1, P 2 etc are sentences y If S is a sentence, S is a sentence (negation) y If S 1 and S 2 are sentences, S 1 S 2 is a sentence (conjunction) y If S 1 and S 2 are sentences, S 1 S 2 is a sentence (disjunction) y If S 1 and S 2 are sentences, S 1 S 2 is a sentence (implication) y If S 1 and S 2 are sentences, S 1 S 2 is a sentence (biconditional) ICS-270 A: Notes 7: 29

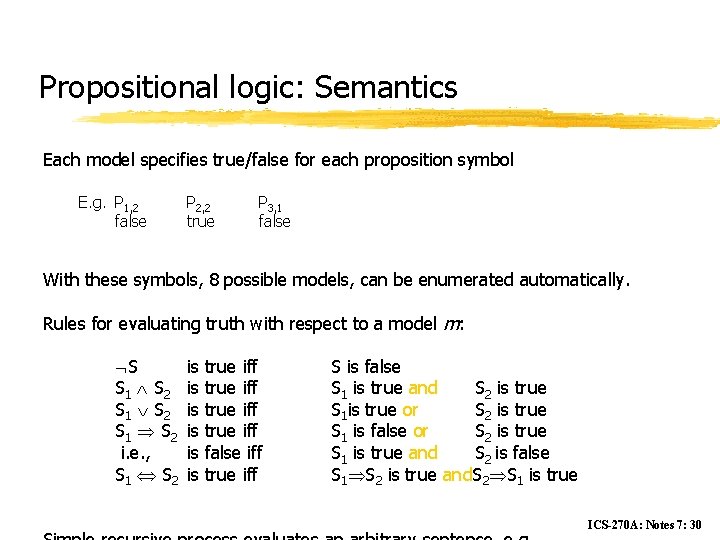
Propositional logic: Semantics Each model specifies true/false for each proposition symbol E. g. P 1, 2 false P 2, 2 true P 3, 1 false With these symbols, 8 possible models, can be enumerated automatically. Rules for evaluating truth with respect to a model m: S S 1 S 2 i. e. , S 1 S 2 is is is true iff false iff true iff S is false S 1 is true and S 2 is true S 1 is true or S 2 is true S 1 is false or S 2 is true S 1 is true and S 2 is false S 1 S 2 is true and. S 2 S 1 is true ICS-270 A: Notes 7: 30

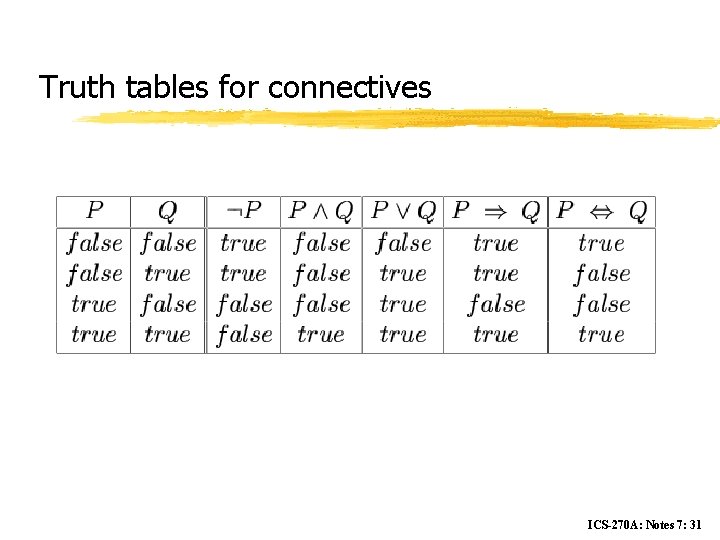
Truth tables for connectives ICS-270 A: Notes 7: 31

Wumpus world sentences Let Pi, j be true if there is a pit in [i, j]. Let Bi, j be true if there is a breeze in [i, j]. P 1, 1 B 2, 1 z "Pits cause breezes in adjacent squares" B 1, 1 B 2, 1 (P 1, 2 P 2, 1) (P 1, 1 P 2, 2 P 3, 1) ICS-270 A: Notes 7: 32

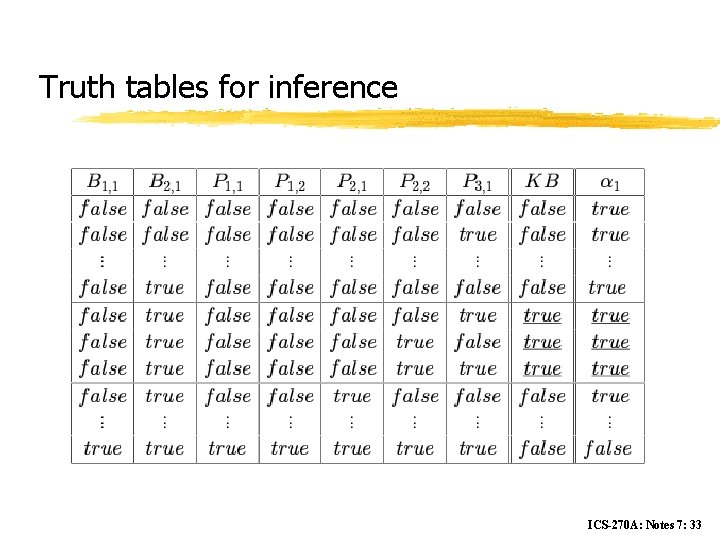
Truth tables for inference ICS-270 A: Notes 7: 33

Inference by enumeration z Depth-first enumeration of all models is sound and complete z For n symbols, time complexity is O(2 n), space complexity is O(n) ICS-270 A: Notes 7: 34

Logical equivalence Two sentences are logically equivalent iff true in same models: α ≡ ß iff α╞ β and β╞α ICS-270 A: Notes 7: 35

Validity and satisfiability A sentence is valid if it is true in all models, e. g. , True, A A, (A B)) B Validity is connected to inference via the Deduction Theorem: KB ╞ α if and only if (KB α) is valid A sentence is satisfiable if it is true in some model e. g. , A B, C A sentence is unsatisfiable if it is true in no models e. g. , A A Satisfiability is connected to inference via the following: KB ╞ α if and only if (KB α) is unsatisfiable ICS-270 A: Notes 7: 36

Validity ICS-270 A: Notes 7: 37

Truth Tables z Truth tables can be used to compute the truth value of any wff. z Can be used to find the truth of z Given n features there are 2 n different worlds, different interpretations. z Interpretation: any assignment of true and false to atoms z An interpretation satisfies a wff (sentence) if the wff is assigned true under the interpretation z A model: An interpretation is a model of a wff if the wff is satisfied in that interpretation. z Satisfiability of a wff can be determined by the truth-table y Bat_on and turns-key_on Engine-starts z Wff is unsatisfiable or inconsistent it has no models y y ICS-270 A: Notes 7: 38

Rules of inference ICS-270 A: Notes 7: 39

Proof methods z Proof methods divide into (roughly) two kinds: y Application of inference rules x. Legitimate (sound) generation of new sentences from old x. Proof = a sequence of inference rule applications Can use inference rules as operators in a standard search algorithm x. Typically require transformation of sentences into a normal form y Model checking xtruth table enumeration (always exponential in n) ICS-270 A: Notes 7: 40

Resolution in Propositional Calculus z Using clauses as wffs y Literal, clauses, conjunction of clauses (cnfs) z Resolution rule: z Resolving (P V Q) and (P V Q) P y Generalize modus ponens, chaining. y Resolving a literal with its negation yields empty clause. z Resolution is sound z Resolution is NOT complete: y P and R entails P V R but you cannot infer P V R From (P and R) by resolution z Resolution is complete for refutation: adding ( P) and ( R) to (P and R) we can infer the empty clause. z Decidability of propositional calculus by resolution refutation: if a sentence w is not entailed by KB then resolution refutation will terminate without generating the empty clause. ICS-270 A: Notes 7: 41

ICS-270 A: Notes 7: 42

Conversion to CNF B 1, 1 (P 1, 2 P 2, 1) 1. Eliminate , replacing α β with (α β) (β α). (B 1, 1 (P 1, 2 P 2, 1)) ((P 1, 2 P 2, 1) B 1, 1) 2. Eliminate , replacing α β with α β. ( B 1, 1 P 1, 2 P 2, 1) ( (P 1, 2 P 2, 1) B 1, 1) 3. Move inwards using de Morgan's rules and double-negation: ( B 1, 1 P 1, 2 P 2, 1) (( P 1, 2 P 2, 1) B 1, 1) ICS-270 A: Notes 7: 44

Converting to Conjunctive clauses (more examples) z 1. Eliminate implications z 2. Reduce the scope of negation sign z 3. Convert to cnfs using the associative and distributive laws ICS-270 A: Notes 7: 45

Resolution algorithm z Proof by contradiction, i. e. , show KB α unsatisfiable ICS-270 A: Notes 7: 46

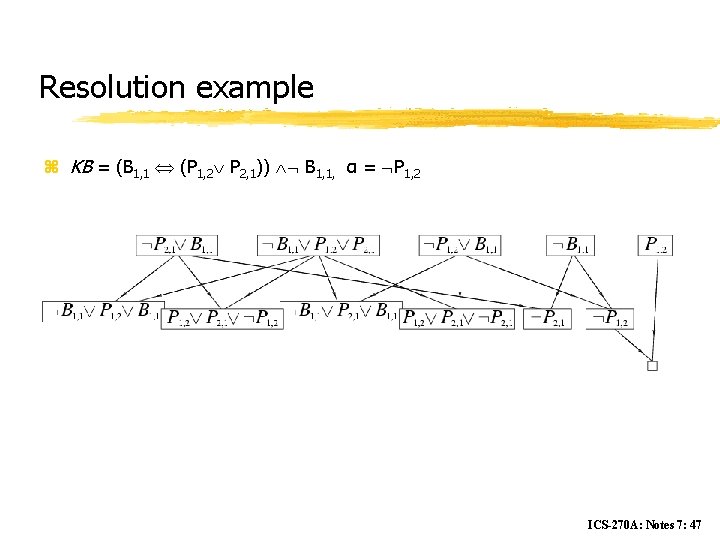
Resolution example z KB = (B 1, 1 (P 1, 2 P 2, 1)) B 1, 1, α = P 1, 2 ICS-270 A: Notes 7: 47

Soundness of resolution ICS-270 A: Notes 7: 48

The party example z If Alex goes, then Beki goes: A B z If Chris goes, then Alex goes: C A z Beki does not go: not B z Chris goes: C z Query: Is it possible to satisfy all these conditions? z Should I go to the party? ICS-270 A: Notes 7: 49

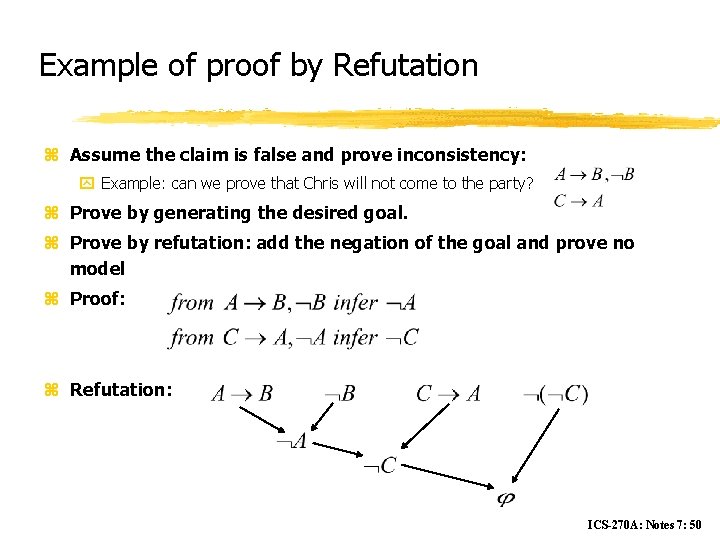
Example of proof by Refutation z Assume the claim is false and prove inconsistency: y Example: can we prove that Chris will not come to the party? z Prove by generating the desired goal. z Prove by refutation: add the negation of the goal and prove no model z Proof: z Refutation: ICS-270 A: Notes 7: 50

Proof by refutation z Given a database in clausal normal form KB y Find a sequence of resolution steps from KB to the empty clauses x. Use the search space paradigm: • States: current cnf KB + new clauses • Operators: resolution • Initial state: KB + negated goal • Goal State: a database containing the empty clause • Search using any search method ICS-270 A: Notes 7: 52

Proof by refutation (contd. ) z Or: y Prove that KB has no model - PSAT x. A cnf theory is a constraint satisfaction problem: • variables: the propositions • domains: true, false • constraints: clauses (or their truth tables) • Find a solution to the csp. If no solution no model. • This is the satisfiability question • Methods: Backtracking arc-consistency unit resolution, local search ICS-270 A: Notes 7: 53

Resolution refutation search strategies z Ordering strategies y Breadth-first, depth-first y I-level resolvents are generated from level-(I-1) or less resolvents y Unit-preference: prefer resolutions with a literal z Set of support: y Allows reslutions in which one of the resolvents is in the set of support y The set of support: those clauses coming from negation of theorem or their decendents. y The set of support strategy is refutation complete z Linear input y Restricted to resolutions when one member is in the input clauses y Linear input is not refutation complete y Example: (PVQ) (P V not Q) (not P V not Q) have no model ICS-270 A: Notes 7: 54

Complexity of propositional inference z Checking truth tables is exponential z Satisfiability is NP-complete z However, frequently generating proofs is easy. z Propositional logic is monotonic y If you can entail alpha from knowledge base KB and if you add sentences to KB, you can infer alpha from the extended knowledge-base as well. z Inference is local y Tractable Classes: Horn, 2 -SAT z Horn theories: y Q <-- P 1, P 2, . . . Pn y Pi is an atom in the language, Q can be false. z Solved by modus ponens or “unit resolution”. ICS-270 A: Notes 7: 55

ICS-270 A: Notes 7: 56

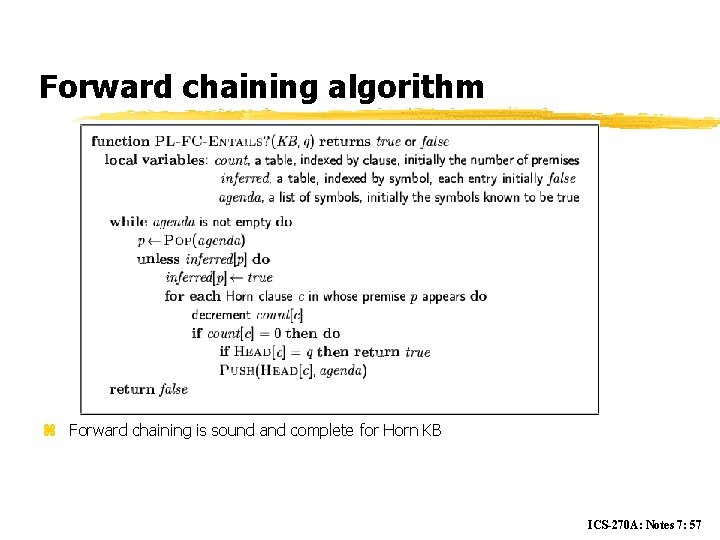
Forward chaining algorithm z Forward chaining is sound and complete for Horn KB ICS-270 A: Notes 7: 57

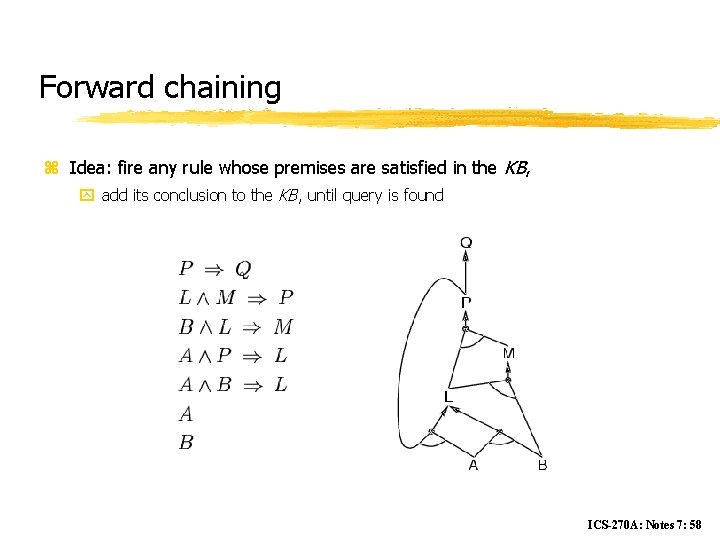
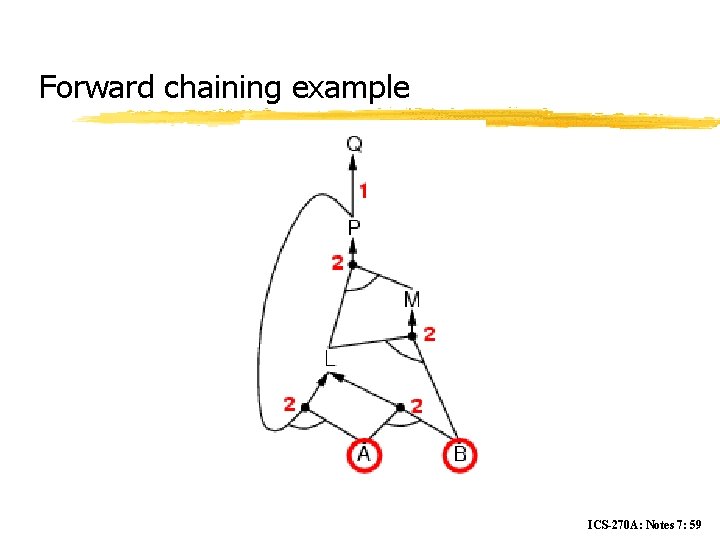
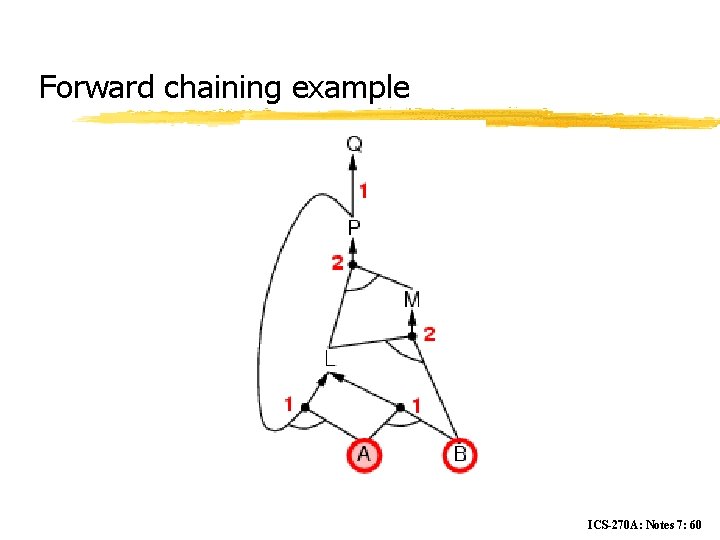
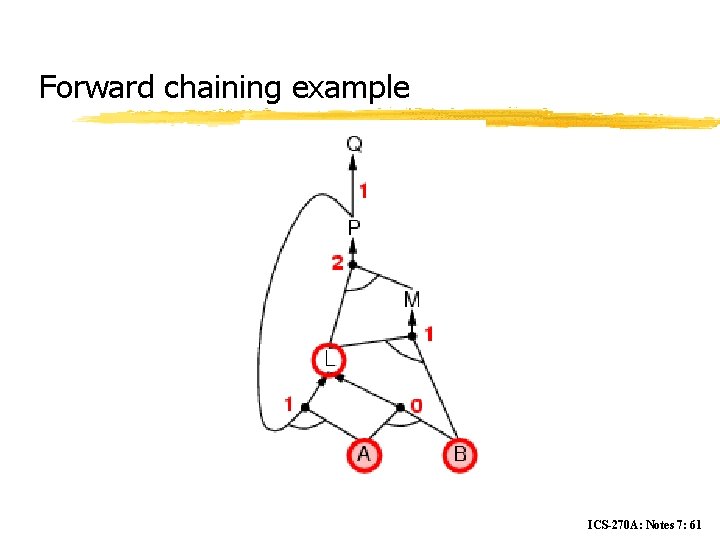
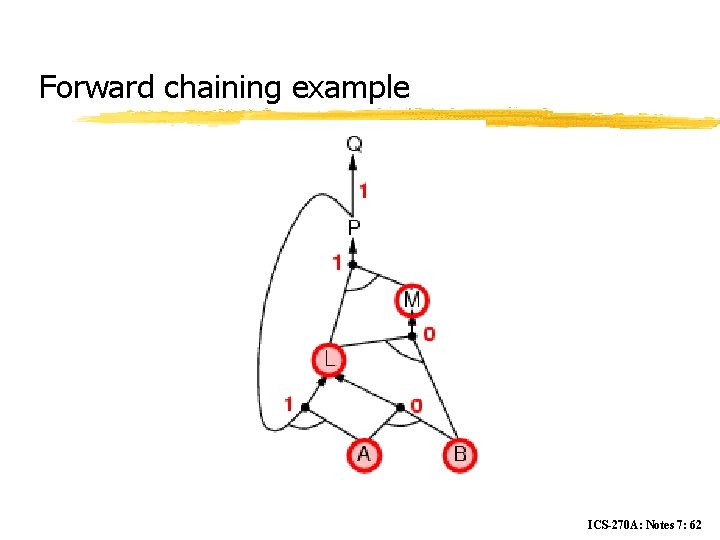
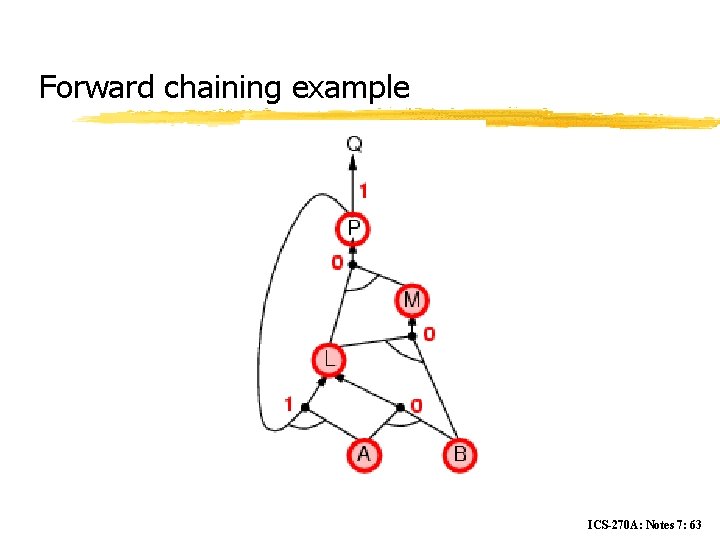
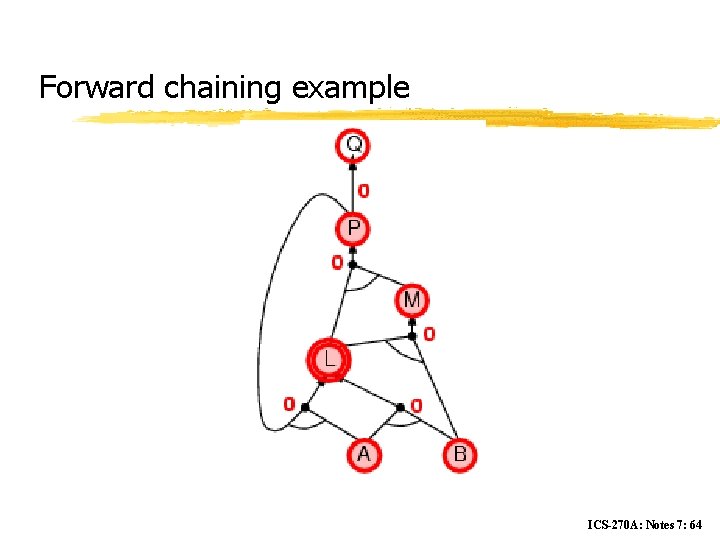
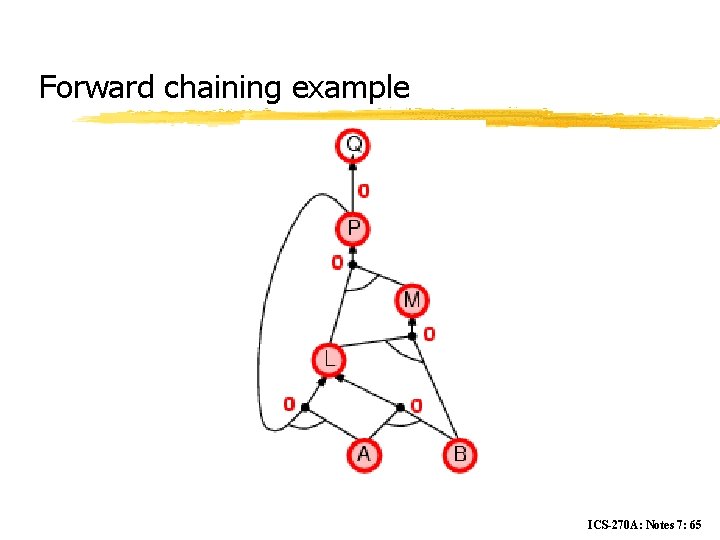
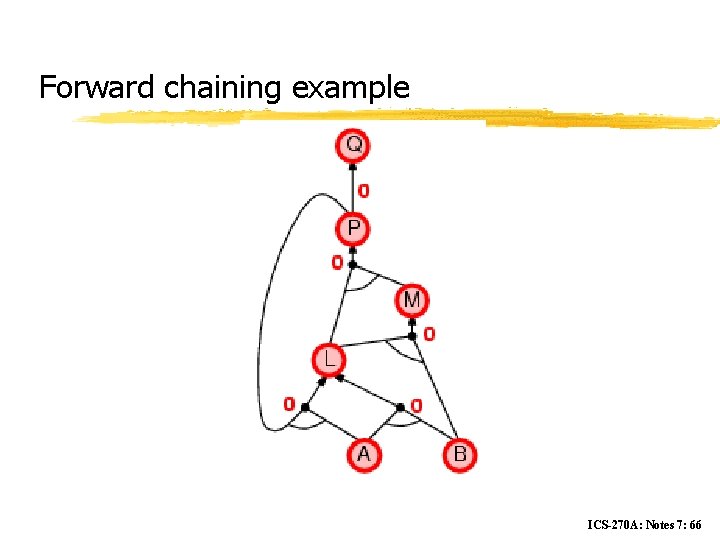
Forward chaining z Idea: fire any rule whose premises are satisfied in the KB, y add its conclusion to the KB, until query is found ICS-270 A: Notes 7: 58

Forward chaining example ICS-270 A: Notes 7: 59

Forward chaining example ICS-270 A: Notes 7: 60

Forward chaining example ICS-270 A: Notes 7: 61

Forward chaining example ICS-270 A: Notes 7: 62

Forward chaining example ICS-270 A: Notes 7: 63

Forward chaining example ICS-270 A: Notes 7: 64

Forward chaining example ICS-270 A: Notes 7: 65

Forward chaining example ICS-270 A: Notes 7: 66

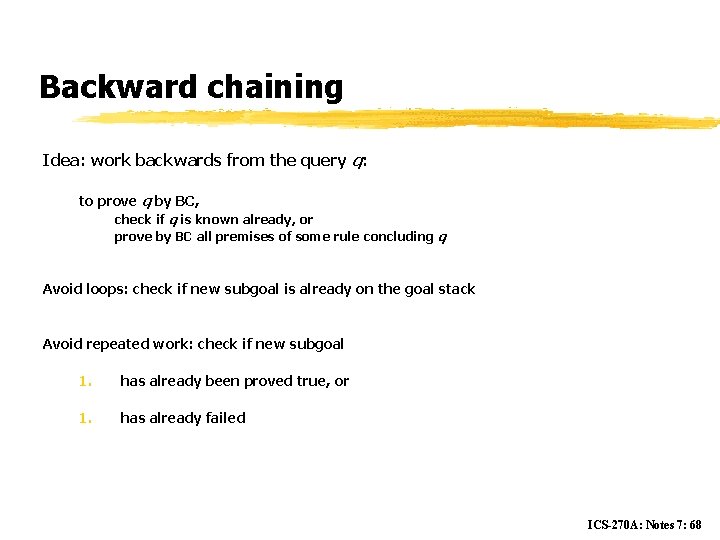
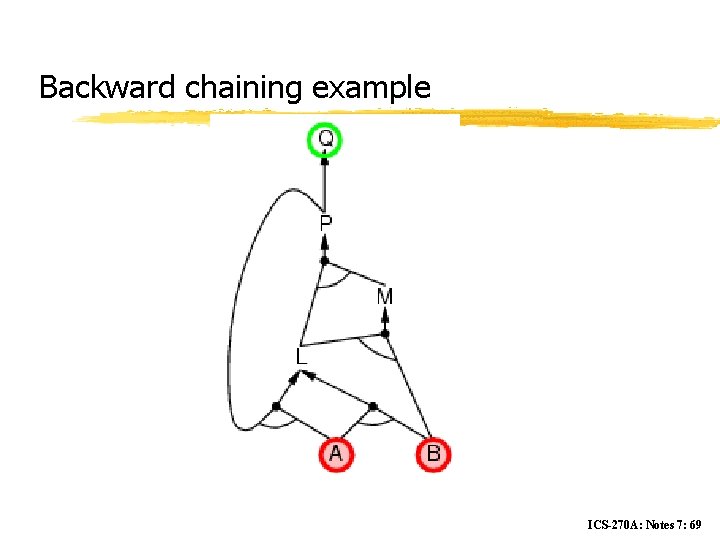
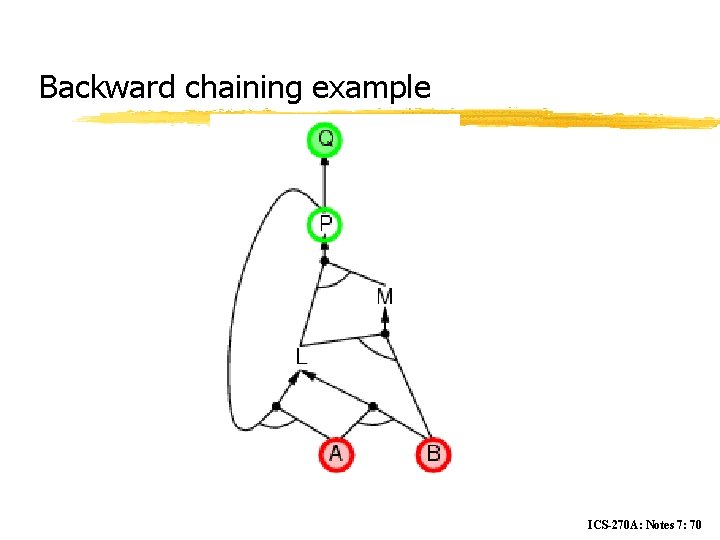
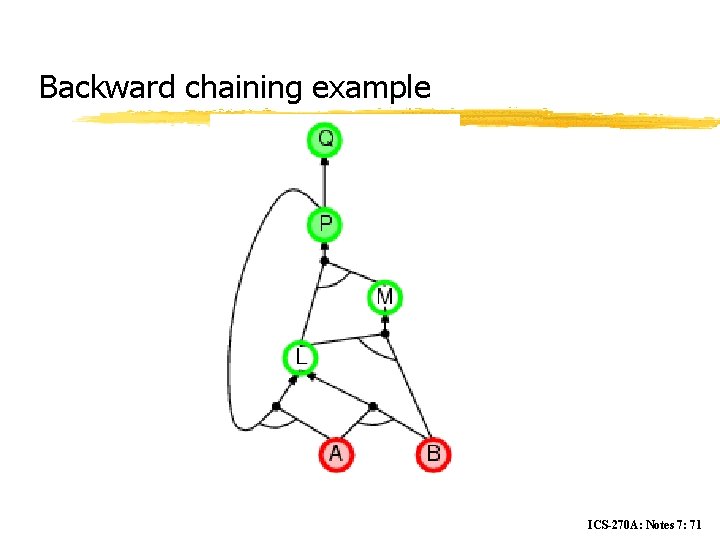
Backward chaining Idea: work backwards from the query q: to prove q by BC, check if q is known already, or prove by BC all premises of some rule concluding q Avoid loops: check if new subgoal is already on the goal stack Avoid repeated work: check if new subgoal 1. has already been proved true, or 1. has already failed ICS-270 A: Notes 7: 68

Backward chaining example ICS-270 A: Notes 7: 69

Backward chaining example ICS-270 A: Notes 7: 70

Backward chaining example ICS-270 A: Notes 7: 71

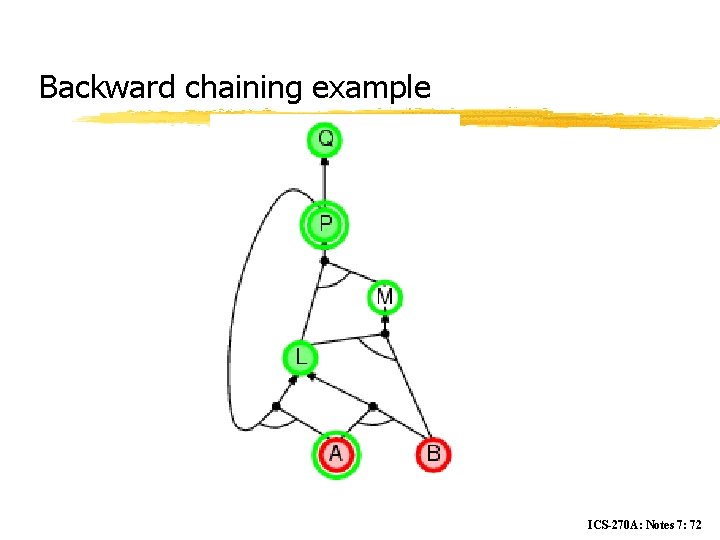
Backward chaining example ICS-270 A: Notes 7: 72

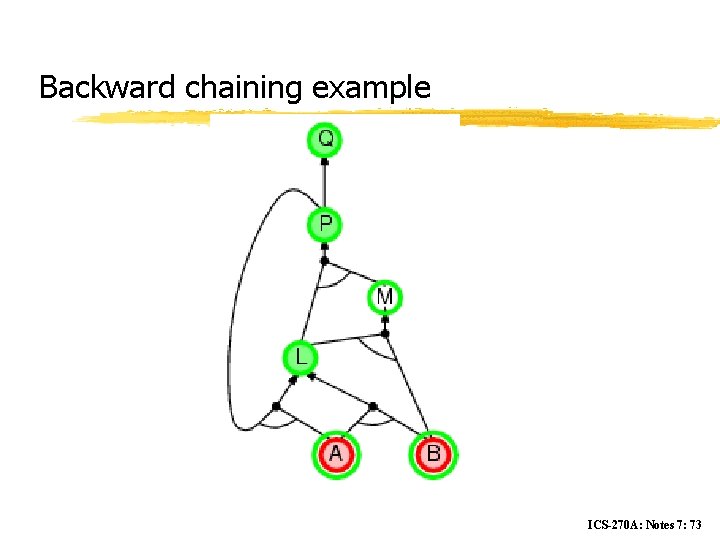
Backward chaining example ICS-270 A: Notes 7: 73

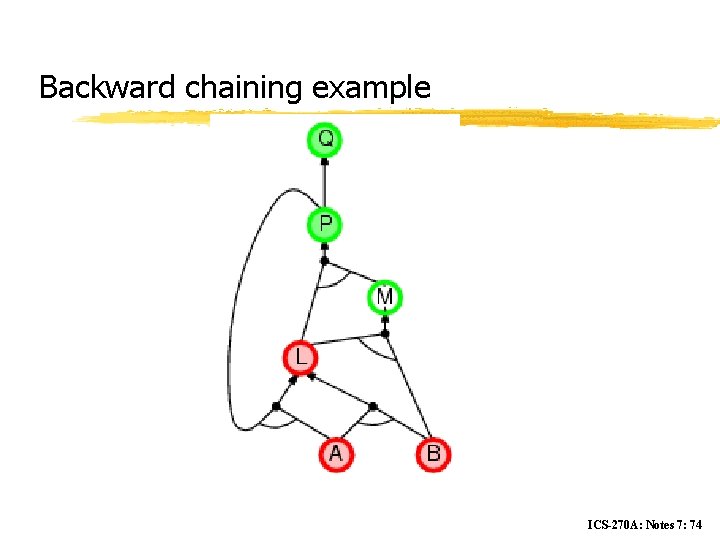
Backward chaining example ICS-270 A: Notes 7: 74

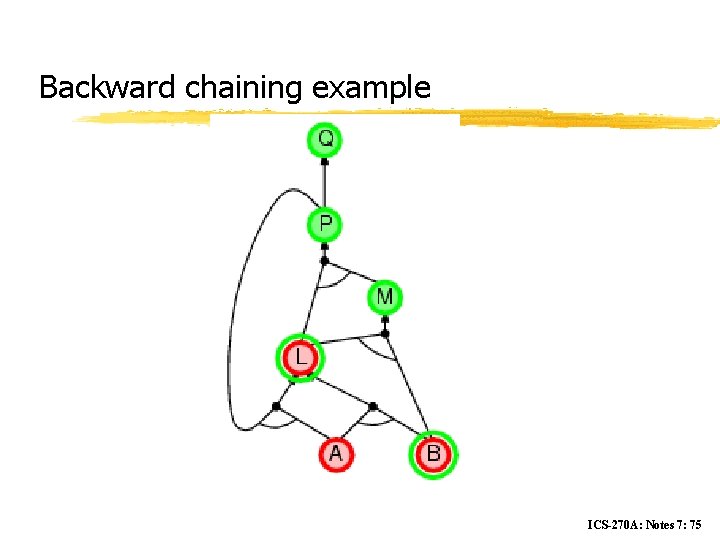
Backward chaining example ICS-270 A: Notes 7: 75

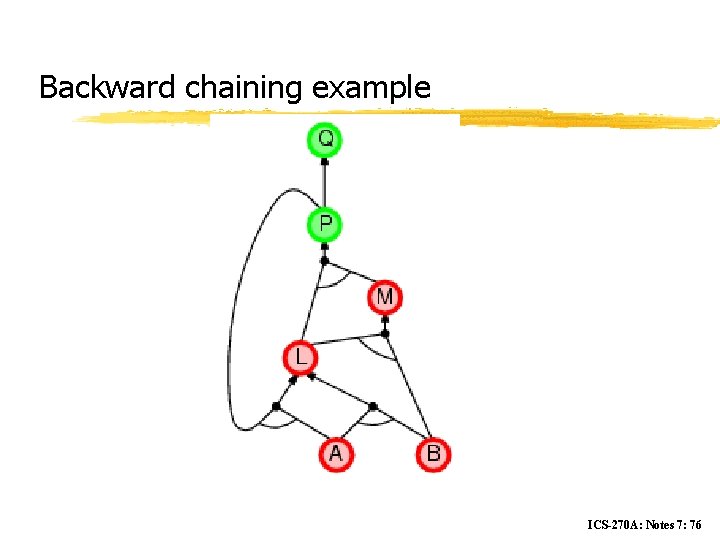
Backward chaining example ICS-270 A: Notes 7: 76

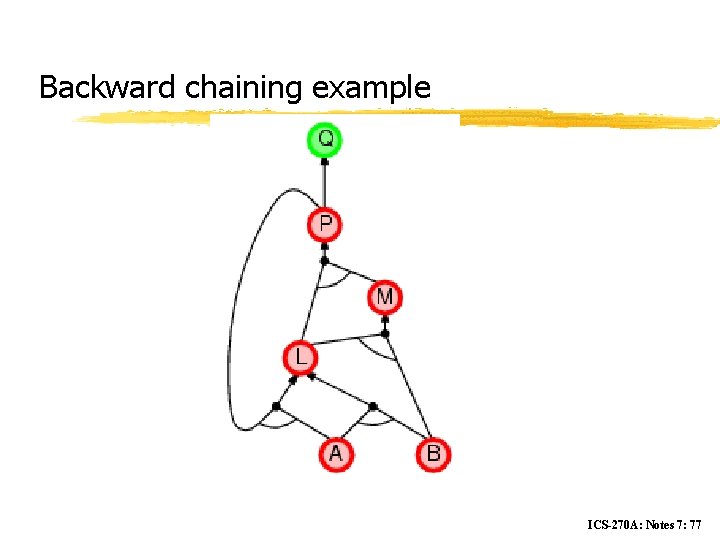
Backward chaining example ICS-270 A: Notes 7: 77

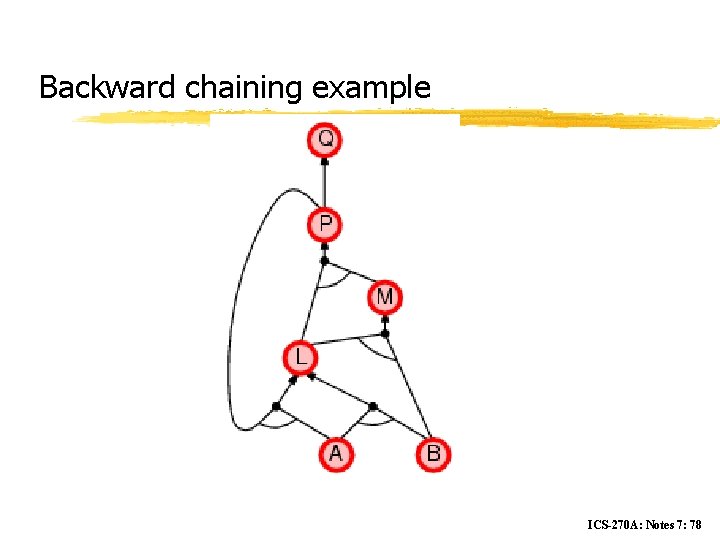
Backward chaining example ICS-270 A: Notes 7: 78

Forward vs. backward chaining z FC is data-driven, automatic, unconscious processing, y e. g. , object recognition, routine decisions z May do lots of work that is irrelevant to the goal z BC is goal-driven, appropriate for problem-solving, y e. g. , Where are my keys? How do I get into a Ph. D program? z Complexity of BC can be much less than linear in size of KB ICS-270 A: Notes 7: 79

Efficient propositional inference Two families of efficient algorithms for propositional inference: Complete backtracking search algorithms z DPLL algorithm (Davis, Putnam, Logemann, Loveland) z Incomplete local search algorithms y Walk. SAT algorithm ICS-270 A: Notes 7: 80

The DPLL algorithm Determine if an input propositional logic sentence (in CNF) is satisfiable. Improvements over truth table enumeration: 1. Early termination A clause is true if any literal is true. A sentence is false if any clause is false. 2. Pure symbol heuristic Pure symbol: always appears with the same "sign" in all clauses. e. g. , In the three clauses (A B), ( B C), (C A), A and B are pure, C is impure. Make a pure symbol literal true. 3. Unit clause heuristic Unit clause: only one literal in the clause The only literal in a unit clause must be true. ICS-270 A: Notes 7: 81

The DPLL algorithm ICS-270 A: Notes 7: 82

The Walk. SAT algorithm z Incomplete, local search algorithm z Evaluation function: The min-conflict heuristic of minimizing the number of unsatisfied clauses z Balance between greediness and randomness ICS-270 A: Notes 7: 83

The Walk. SAT algorithm ICS-270 A: Notes 7: 84

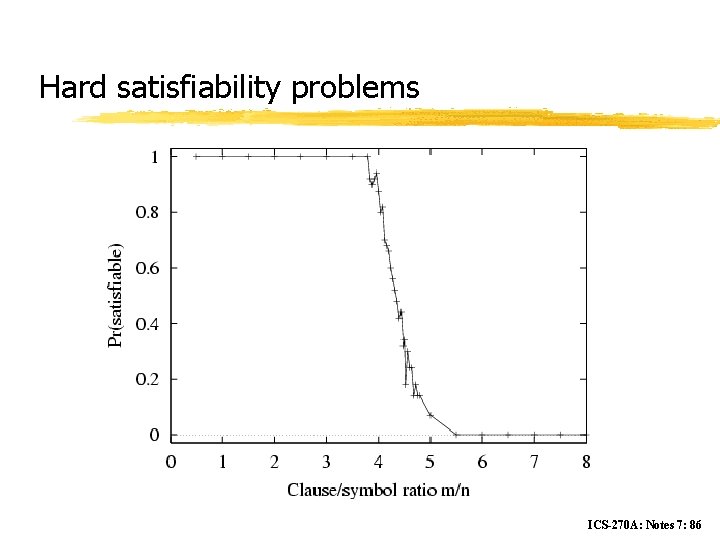
Hard satisfiability problems z Consider random 3 -CNF sentences. e. g. , ( D B C) (B A C) ( C B E) (E D B) (B E C) m = number of clauses n = number of symbols y Hard problems seem to cluster near m/n = 4. 3 (critical point) ICS-270 A: Notes 7: 85

Hard satisfiability problems ICS-270 A: Notes 7: 86

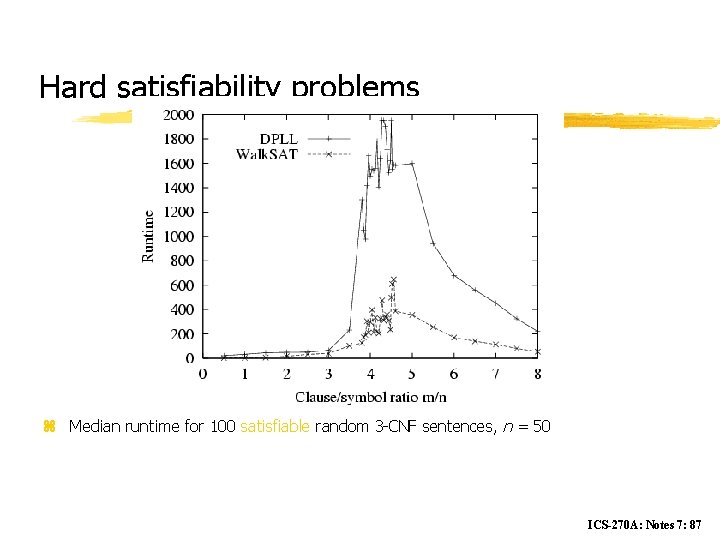
Hard satisfiability problems z Median runtime for 100 satisfiable random 3 -CNF sentences, n = 50 ICS-270 A: Notes 7: 87

Inference-based agents in the wumpus world A wumpus-world agent using propositional logic: P 1, 1 W 1, 1 Bx, y (Px, y+1 Px, y-1 Px+1, y Px-1, y) Sx, y (Wx, y+1 Wx, y-1 Wx+1, y Wx-1, y) W 1, 1 W 1, 2 … W 4, 4 W 1, 1 W 1, 2 W 1, 1 W 1, 3 … 64 distinct proposition symbols, 155 sentences ICS-270 A: Notes 7: 88

ICS-270 A: Notes 7: 89

ICS-270 A: Notes 7: 90