NOTES 3 1 part 2 Significant Figures Significant































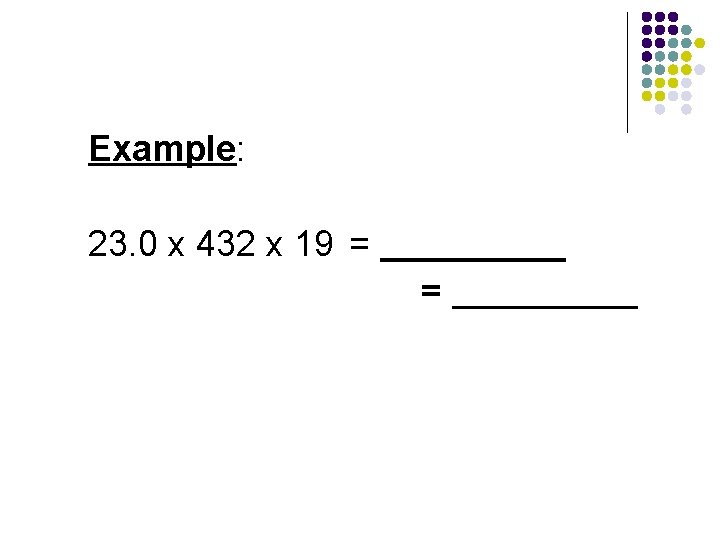




- Slides: 37

NOTES: 3. 1, part 2 Significant Figures

Significant Figures: l l l The “sig figs” in a measurement include all of the digits that are known, plus a last digit that is estimated The # of sig figs in a measurement depends on the precision of the instrument being used How do we determine which digits are significant?

THE “RULES” FOR SIG FIGS!!

1) All non-zero numbers are significant. l l l EXAMPLES: 672 34 1, 245 24, 346 -

1) All non-zero numbers are significant. l l l EXAMPLES: 672 34 1, 245 24, 346 - 3 sig figs 2 sig figs 4 sig figs 5 sig figs

2) Zeroes between two non zero numbers are significant. l l l l EXAMPLES: 202 1. 01 1, 305 10, 001 3, 002 62, 004 -

2) Zeroes between two non zero numbers are significant. l l l l EXAMPLES: 202 1. 01 1, 305 10, 001 3, 002 62, 004 - 3 sig figs 4 sig figs 5 sig figs

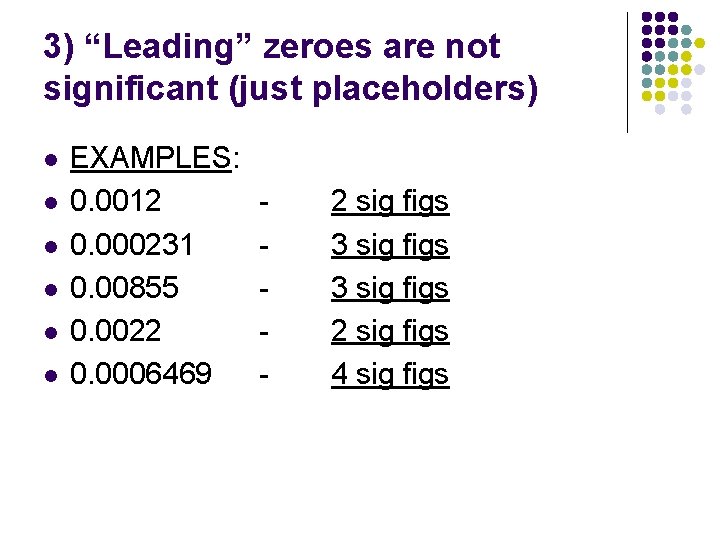
3) “Leading” zeroes are not significant (just placeholders) l l l EXAMPLES: 0. 0012 0. 000231 0. 00855 0. 0022 0. 0006469 -

3) “Leading” zeroes are not significant (just placeholders) l l l EXAMPLES: 0. 0012 0. 000231 0. 00855 0. 0022 0. 0006469 - 2 sig figs 3 sig figs 2 sig figs 4 sig figs

4) Final or trailing zeroes are not significant UNLESS there is a decimal point in the number. l l l l EXAMPLES: 150 22. 0 12, 500 0. 00240 5, 250 0. 02300 0. 000350 -

4) Final or trailing zeroes are not significant UNLESS there is a decimal point in the number. l l l l EXAMPLES: 150 22. 0 12, 500 0. 00240 5, 250 0. 02300 0. 000350 - 2 sig figs 3 sig figs 4 sig figs 3 sig figs

5) Powers of ten are not significant l l l EXAMPLES: 1. 50 X 102 8. 890 x 104 7. 0 x 108 4. 010500 x 1010 6. 35 x 10 -12 -

5) Powers of ten are not significant l l l EXAMPLES: 1. 50 X 102 8. 890 x 104 7. 0 x 108 4. 010500 x 1010 6. 35 x 10 -12 - 3 sig figs 4 sig figs 2 sig figs 7 sig figs 3 sig figs

PRACTICE: Determine how many significant figures are in each of the following measurements 1) 2) 3) 4) 5) 6) 0. 0034050 L 33. 600 m 7500. 0 g 47, 900 mm 7, 000, 001 miles 8. 07 Hz ___________ ___________

PRACTICE: Determine how many significant figures are in each of the following measurements 1) 2) 3) 4) 5) 6) 0. 0034050 L 33. 600 m 7500. 0 g 47, 900 mm 7, 000, 001 miles 8. 07 Hz 5 ___________ 5 5 ______ 3 ______ 10 ______ 3 ______

Sig Figs in Calculations: l Find the area of a floor that measures 7. 7 meters by 5. 4 meters: l AREA =

Sig Figs in Calculations: l Find the area of a floor that measures 7. 7 meters by 5. 4 meters: l AREA = 41. 58 m 2

But wait!. . . l l l The calculated answer has 4 sig figs, but each measurement used in the calculation only had 2! The calculated area cannot be more precise than the measured values used to obtain it! SO…we “round” the answer to the appropriate # of sig figs

ROUNDING: l l l After you have determined how many sig figs the answer can have, round to that many digits: If the last significant digit is less than 5: leave the last sig fig as is; If the last significant digit is 5 or greater: round up!

Practice Problems: How many sig figs in each of the following? 1) 123 meters 2) 40, 506 meters 3) 9. 8000 x 104 m 4) 0. 07080 m 5) 98, 000 m -

Practice Problems: How many sig figs in each of the following? 1) 123 meters 3 sig figs 2) 40, 506 meters 5 sig figs 3) 9. 8000 x 104 m 5 sig figs 4) 0. 07080 m 4 sig figs 5) 98, 000 m 2 sig figs

More practice…Round the following measurements off so that they each contain 3 significant figures. 1) 366. 2 L 2) 9, 047, 022 mg 3) 12. 76 g 4) 999. 9 J ___________

More practice…Round the following measurements off so that they each contain 3 significant figures. 1) 366. 2 L 2) 9, 047, 022 mg 3) 12. 76 g 4) 999. 9 J ______ 366 L ______ 9, 050, 000 mg 12. 8 g ______ 1. 00 x 103 J ______ Notice this one must be in scientific notation to have 3 sig. figs.

NOTES: 3. 1, part 2 – Operations With Significant Figures!!

ADDITION AND SUBTRACTION l First add or subtract, then round the answer to the last decimal place they have in common. 25. 46 + 221. 3 = = 1. 6251 -0. 543 = =

ADDITION AND SUBTRACTION l First add or subtract, then round the answer to the last decimal place they have in common. 25. 46 + 221. 3 = 246. 76 = 246. 8 1. 6251 -0. 543 = 1. 0821 = 1. 082

Example: 123. 25 + 46. 0 + 86. 257 = =

Example: 123. 25 + 46. 0 + 86. 257 = 255. 507 = 255. 5 The answer is expressed as 255. 5 since 46. 0 has only one decimal place.

Examples: a. 15. 2 + 5. 0892 = = c. 17. 1 - 0. 77 = = = b. 10. 8164 - 8. 22 = d. 2. 1 + 4. 235 + 3. 92 = =

Examples: a. 15. 2 + 5. 0892 = 20. 2892 = 20. 3 c. 17. 1 - 0. 77 = 16. 33 = 16. 3 b. 10. 8164 - 8. 22 = 2. 5964 = 2. 60 d. 2. 1 + 4. 235 + 3. 92 = 10. 255 = 10. 3

MULTIPLICATION AND DIVISION l Multiply or divide first, then round the answer to the same number of sig figs as the smallest number you started with. 1. 311 x 2. 20 = = 6. 884 / 2 = =

MULTIPLICATION AND DIVISION l Multiply or divide first, then round the answer to the same number of sig figs as the smallest number you started with. 1. 311 x 2. 20 = 2. 8842 = 2. 88 6. 884 / 2 = 3. 441 =3
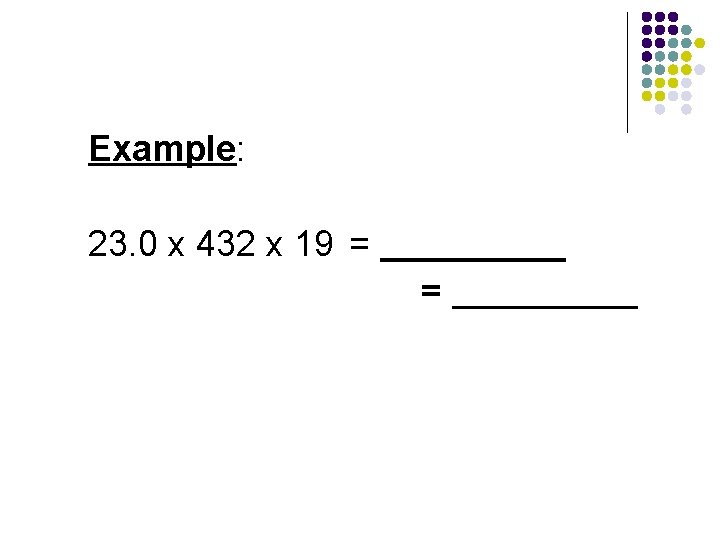
Example: 23. 0 x 432 x 19 = =

Example: 23. 0 x 432 x 19 = 188, 784 = 190, 000 The answer is expressed as 190, 000 or 1. 9 x 105 since 19 has only two sig. figs.

Examples: a. b. c. d. e. 3. 214 x 4. 24 = 6. 8 x 3. 145 = 122. 82 / 2. 00 = 0. 072 / 4. 36 = 5. 82 x 760 x 325 723 x 273 =

Examples: a. b. c. d. e. 3. 214 x 4. 24 = 6. 8 x 3. 145 = 122. 82 / 2. 00 = 0. 072 / 4. 36 = 5. 82 x 760 x 325 723 x 273 = 13. 6 21 61. 4 0. 17 7. 3

Perform the following calculations. Round your answers to the proper # of sig. figs. 1) 36. 57 m / 3. 21 s = 2) 41. 376 g + 13. 3 g + 42. 9 g = 3) 5. 67 m x 13. 44 m = 4) (5. 83 m / 2. 67 s) / 2. 1 s = 5) 9. 374 V x 6. 0 = ______ 11. 4 m/s ______ 97. 6 g 76. 2 m 2 ___________ 1. 0 m/s 2 ______ 56 V From now on, we will round all our answers to the correct # of significant figures.