Notes 25 Using Permutation Formula 942021 1 RECAP

Notes #25 Using Permutation Formula 9/4/2021 1

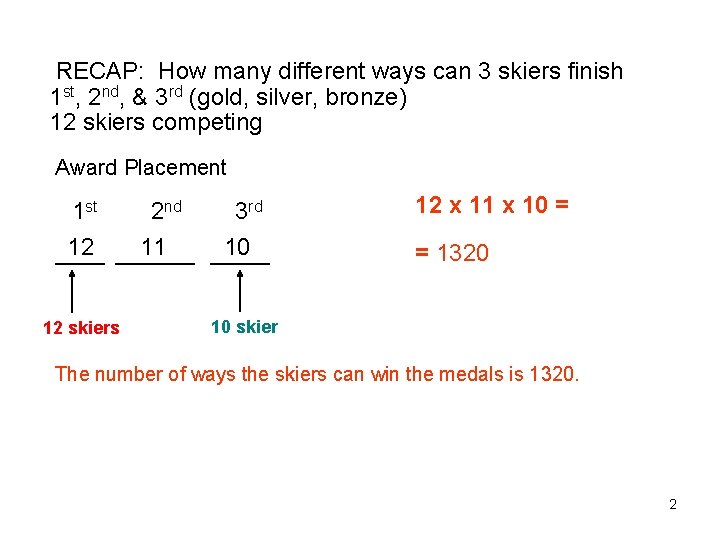
RECAP: How many different ways can 3 skiers finish 1 st, 2 nd, & 3 rd (gold, silver, bronze) 12 skiers competing Award Placement 1 st 12 _____ 2 nd 11 ____ 12 skiers 3 rd 10 ______ 12 x 11 x 10 = = 1320 10 skier The number of ways the skiers can win the medals is 1320. 2

A Formula for Permutations • Permutations of “n” things taken “r” at a time. 9/4/2021 Section 11. 2 3

USING PERMUTATION FORMULA Ex 1: How many different ways can 3 of the skiers finish 1 st, 2 nd, & 3 rd (gold, silver, bronze)? (TOTAL: 12 Skiers) It can be set up as the number of permutations of 12 things taken 3 at a time. Let “n” = 12; Let “r” = 3 12 P 3 = 12! (12 -3)! = 12! 9! • 12*11*10*9*8*7*6*5*4*3*2*1 • 12*11*10 = 1320 =

Example 2 Using the Formula for Permutations • You and 19 of your friends have decided to form a business. The group needs to choose three officers– A CEO, an Operating Manager, and a Treasurer. In how many ways can those offices be filled? Set Up: (3 Steps) 1) Let n = 20 people; Let r = 3 positions to select 2) Complete the Permutation Formula: ________ 3) SHOW WORK . 9/4/2021 ANS: There are 6840 ways these positions can be filled. 5

EX 3: Using the letters in the word ” SQUARE ", how many 6 -letter arrangements, with no repetitions, are possible if the first letter is a vowel? ; Where 0! = 1 SET UP: 1) Start with the specific condition/restriction (3 vowels: U, A, E) 2) Multiply the restriction with the Permutation Formula Let n = 5 letters left ; Let r = 5 choices 3) SHOW WORK: 3 · 5 P 5 = # of Vowels (First letter) = =

A Formula for Permutations of Duplicate Items • Permutations of Duplicate Items The number of permutations of “n” items, where “p” items are identical, “q” items are identical, “r” items are identical, and so on, is given by: 7

Example 1 Using the Formula for Permutations of Duplicate Items • In how many distinct ways can the letters of the word MISSISSIPPI be arranged? SET UP: (3 Steps) 1) The word contains 11 letters (n = 11) • Find p, q, & r - Four “I’s” are identical (p = 4) - Four “S’s” are identical (q = 4) - Two “P’s” are identical (r = 2) 3) Apply Formula for Permutation of Duplicate Items 8