NOTES 12 3 Surface Area of Circular Solids

NOTES 12. 3 Surface Area of Circular Solids

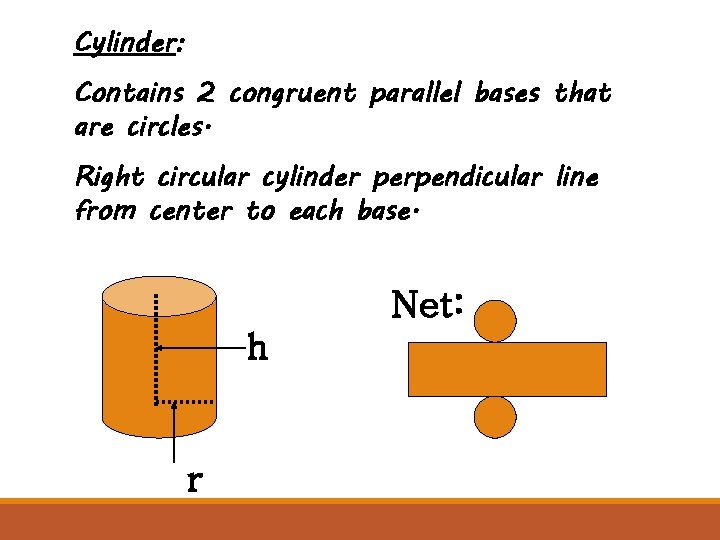
Cylinder: Contains 2 congruent parallel bases that are circles. Right circular cylinder perpendicular line from center to each base. Net: h r

Theorem 113: h The lateral area of a cylinder is equal to the product of the height and the circumference of the base. LAcyl = Ch = 2πrh (C = circumference, h= height) The total area of a cylinder is the sum of the cylinder’s lateral area and the areas of the two bases. T. A. = 2πr 2 + 2πrh r

Find the surface area following cylinder: 7 cm (total) of the TA = 2πr 2 + 2πrh TA = 2π(72) + 2π(7)(10) 10 cm TA = 98π + 140π TA = 238π cm 2

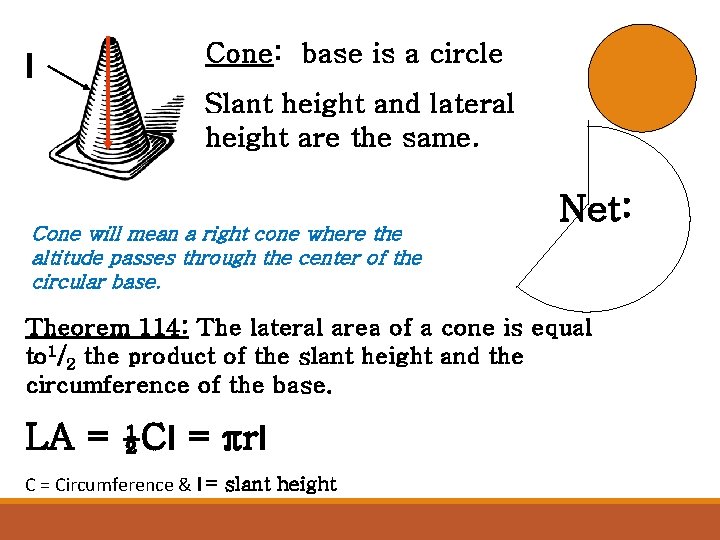
l Cone: base is a circle Slant height and lateral height are the same. Cone will mean a right cone where the altitude passes through the center of the circular base. Net: Theorem 114: The lateral area of a cone is equal to 1/2 the product of the slant height and the circumference of the base. LA = ½Cl = πrl C = Circumference & l = slant height

The total surface area of a cone is the sum of the lateral area and the area of the base. TA = πr 2 + πrl Find the surface area of the cone. The diameter is 6 & the slant height is 8. TA = πr 2 + πrl = π(3)2 + π3(8) = 9π + 24π = 33π units 2

Sphere: has NO lateral edges & No lateral area Postulate: TA = 4πr 2 r = radius of the sphere

Find the total area of the sphere: TA = 4πr 2 = 4π52 = 100π units 2

As a team, find the surface area of the following shape. Only find the area of the parts you can see. 17 cm 16 cm 10 cm

1. Lateral area of a cone, πrl = π8(17) = 136π 2. Plus the lateral area of the cylinder, 2πrh = 2π(8)(10) = 160π 3. Plus the surface of the hemisphere. 4πr 2 = (1/2)4π(82) = 128π 4. Add them up: 136π + 160π + 128π = 424π units 2