Notes 10 Probability Venn diagrams Mutually Exclusive Events

Notes #10 Probability & Venn diagrams

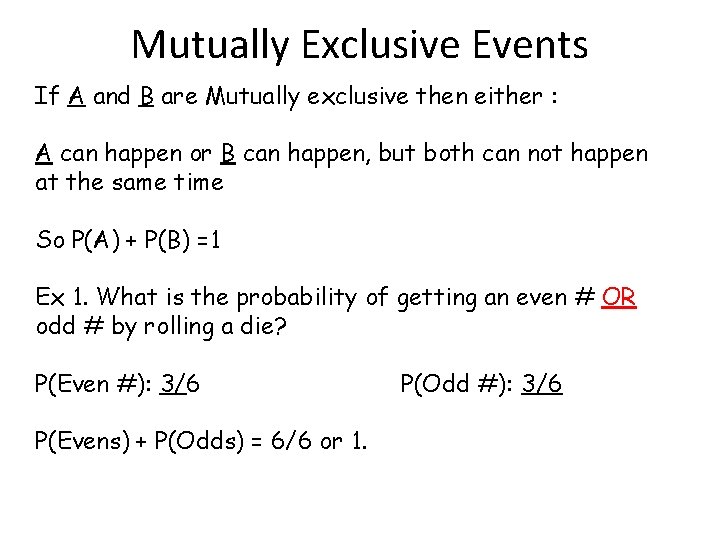
Mutually Exclusive Events If A and B are Mutually exclusive then either : A can happen or B can happen, but both can not happen at the same time So P(A) + P(B) =1 Ex 1. What is the probability of getting an even # OR odd # by rolling a die? P(Even #): 3/6 P(Evens) + P(Odds) = 6/6 or 1. P(Odd #): 3/6

Mutually Non-Exclusive (Compatible) Events • Two events A and B are said to be mutually non exclusive events if both the events A and B have at least one common outcome between them. Ex 2: What is the probability of getting an odd # and getting a # < 4 from rolling a die?

Non-Exclusive Probability Events 1. Let ‘X’ = Event of getting an ‘odd #’ Setting Up Mutually 2. ‘Y’ = event of getting ‘Less than 4’ 3. The events of getting an odd number is (X) = {1, 3, 5} The curly braces are the customary notation for sets. 4. The events of getting # < 4 is (Y) = {1, 2, 3} 5. Between the events X and Y the common outcomes are 1 and 3 • Therefore, the events X and Y are mutually nonexclusive events.

Why Use Venn Diagrams to Solve for Probabilities? ANS: B/C it’s another visual way of representing a Probability space

Ex 3: A die is rolled an even number is obtained, show this in a Venn diagram. This is an exclusive event (no #s in common) Set-Up 1. Label One Circle (A): Even # Event 2. Label other Circle (A’): Complement Event (#s not even) 3. Determine P(A): 3/6 or 0. 5 A’ 1, 3, 5 A 2, 4, 6

Notations for Venn Diagrams The pinkish shaded regions marked the solution "regions" in the Venn diagrams Problem: Given a universe that has 1, 2, 3, & 4. A = {1, 2} & B = {2, 3}, where ‘ 4’ is not included.

Notations for Venn Diagrams

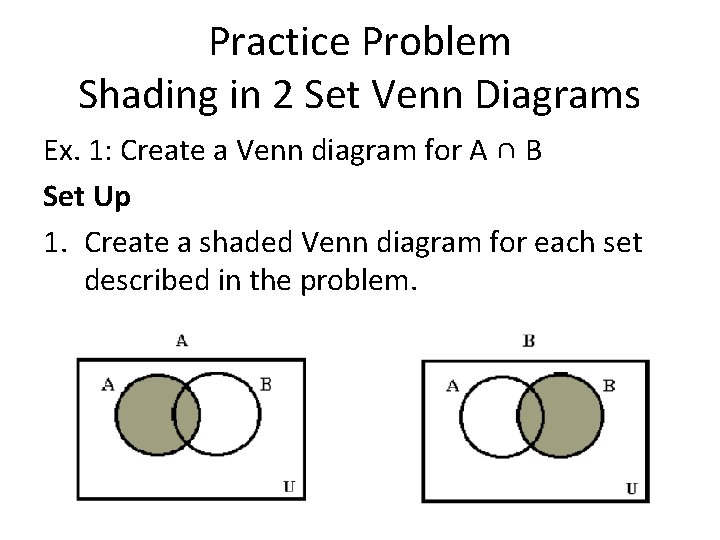
Practice Problem Shading in 2 Set Venn Diagrams Ex. 1: Create a Venn diagram for A ∩ B Set Up 1. Create a shaded Venn diagram for each set described in the problem.

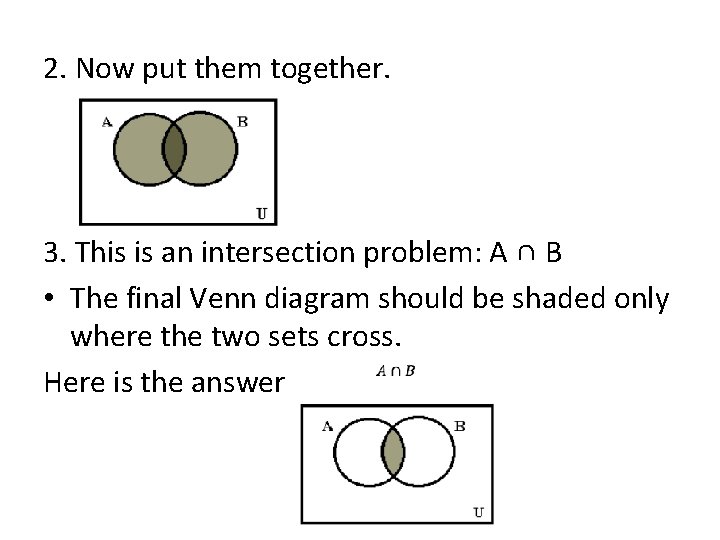
2. Now put them together. 3. This is an intersection problem: A ∩ B • The final Venn diagram should be shaded only where the two sets cross. Here is the answer:

Notations for Venn Diagrams EX 4: Let's say that our universe contains the numbers 1, 2, 3, and 4. Let A be the set containing the numbers 1 and 2; that is, A = {1, 2}. (Warning: The curly braces are the customary notation for sets. Do not use parentheses or square brackets. ) Let B be the set containing the numbers 2 and 3; that is, B = {2, 3}.

Classwork/HW • Complete #1 & #2 • Finish #3 -#8 for HW

Recap Event - An event is the situation in which we are interested Probability- Is the chance of that event happening Outcome – Is what happens (result of experiment) Prob (Event ) = Number of ways of event happening Total possible outcomes Prob (Not Event) = 1 - Prob(Event)