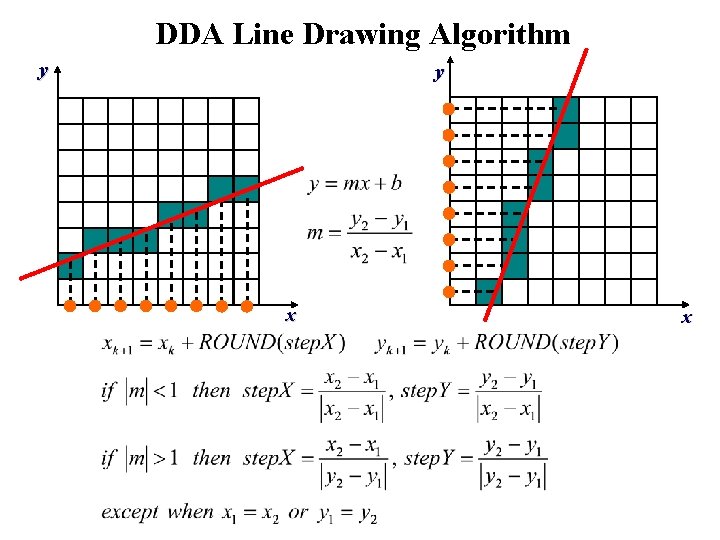
NOTE DDA Line Drawing Algorithm y y x

NOTE

DDA Line Drawing Algorithm y y x x

Bresenham’s Line Drawing Algorithm

Bresenham’s Line Drawing Algorithm

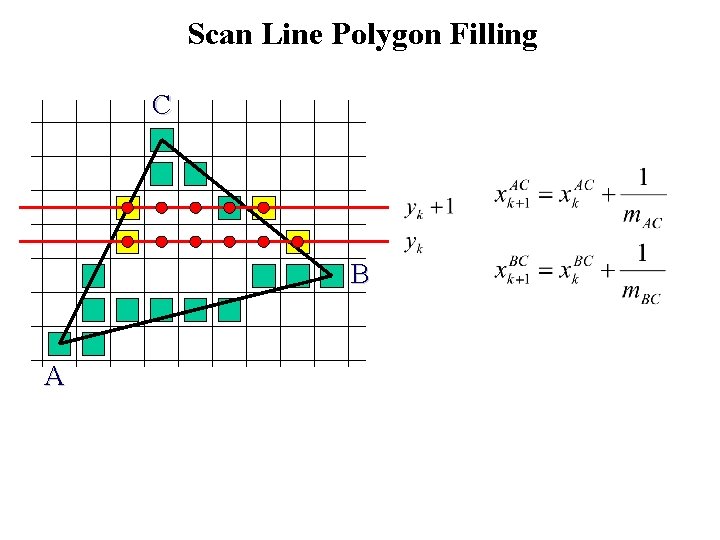
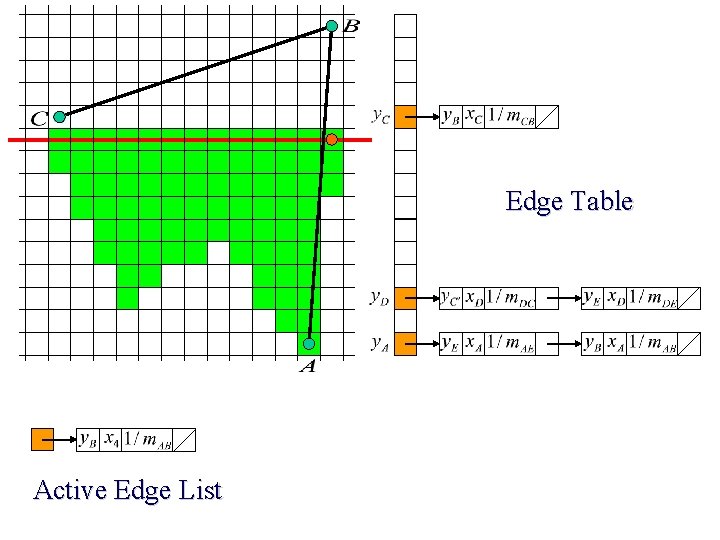
Scan Line Polygon Filling C B A

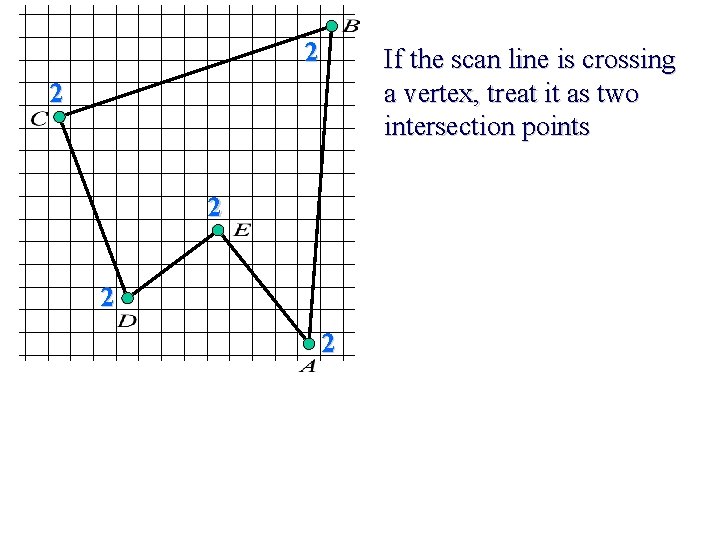
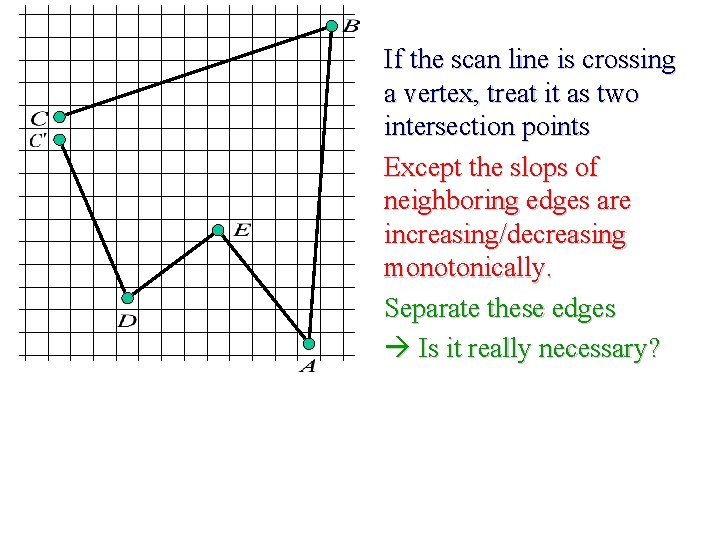
2 If the scan line is crossing a vertex, treat it as two intersection points 2 2

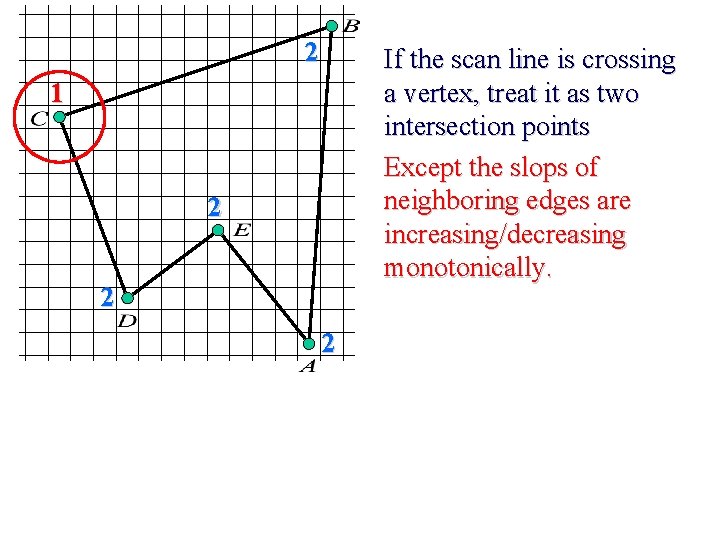
2 If the scan line is crossing a vertex, treat it as two intersection points Except the slops of neighboring edges are increasing/decreasing monotonically. 1 2 2 2

If the scan line is crossing a vertex, treat it as two intersection points Except the slops of neighboring edges are increasing/decreasing monotonically. Separate these edges Is it really necessary?

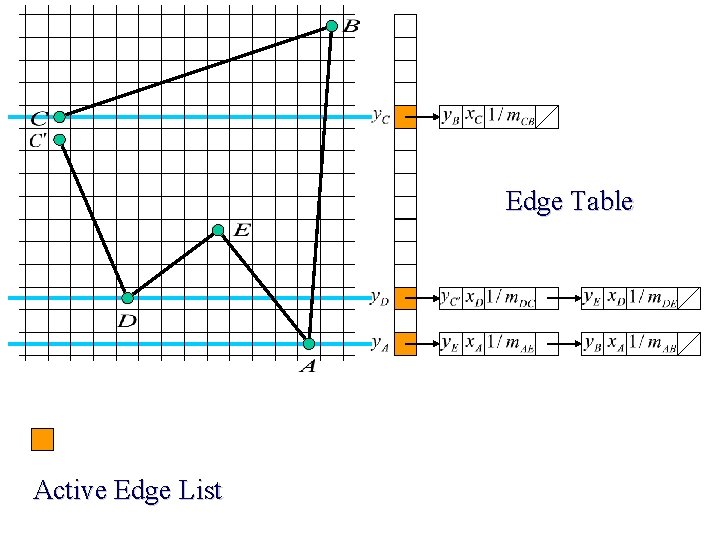
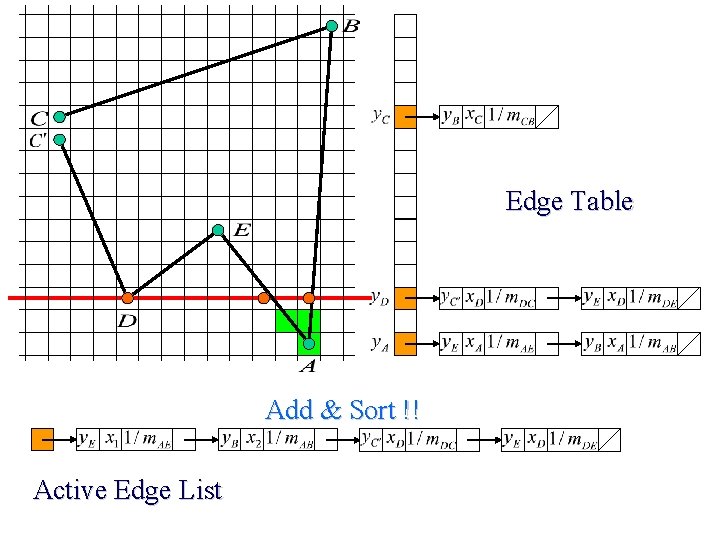
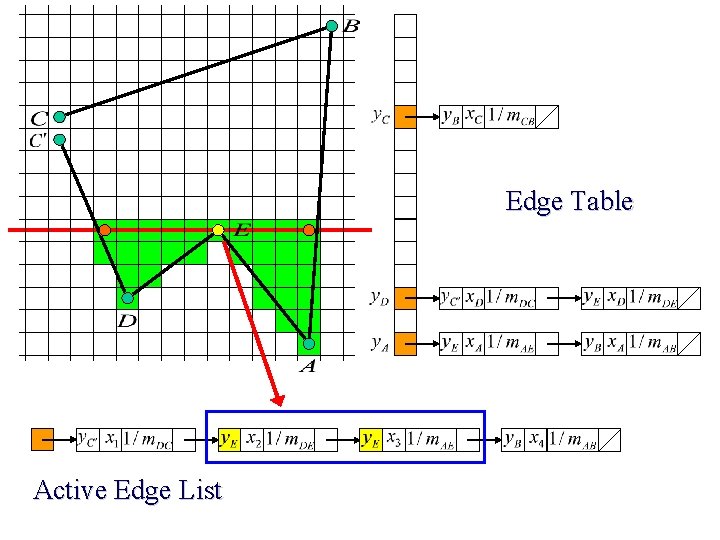
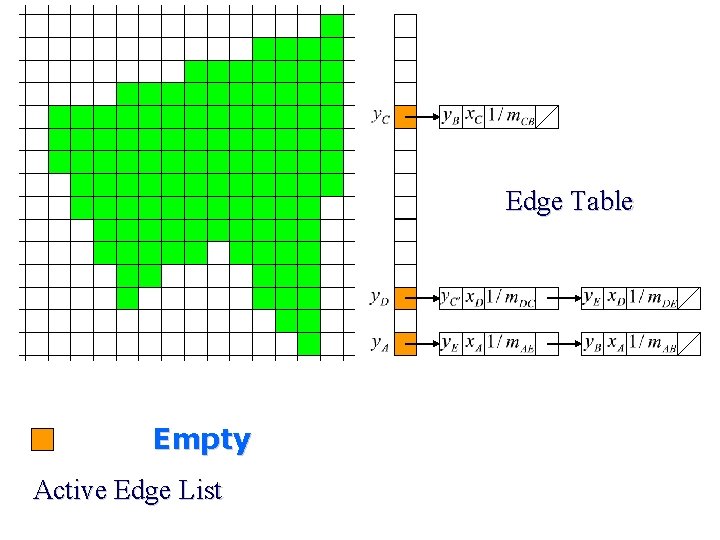
Edge Table Active Edge List

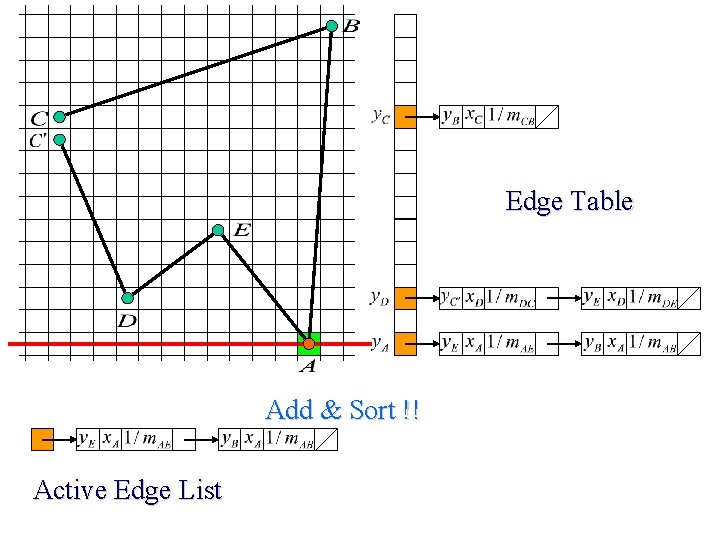
Edge Table Add & Sort !! Active Edge List

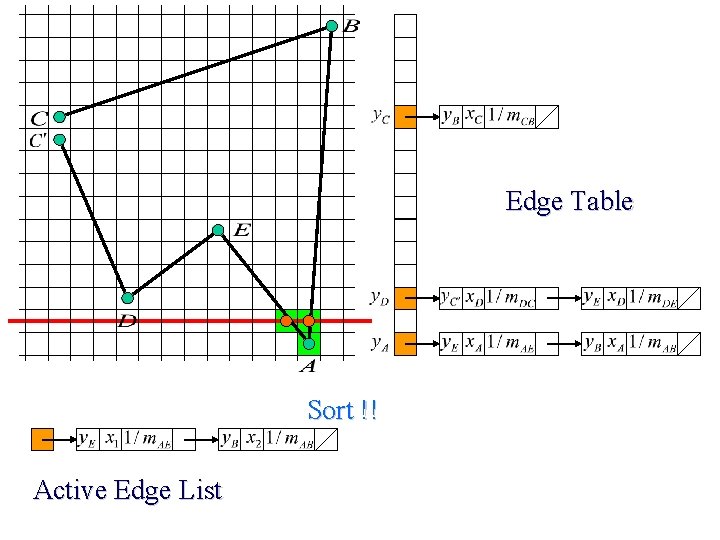
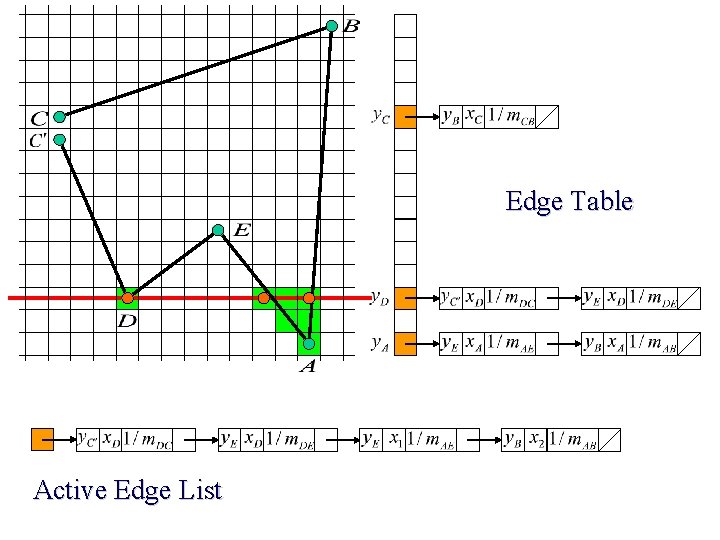
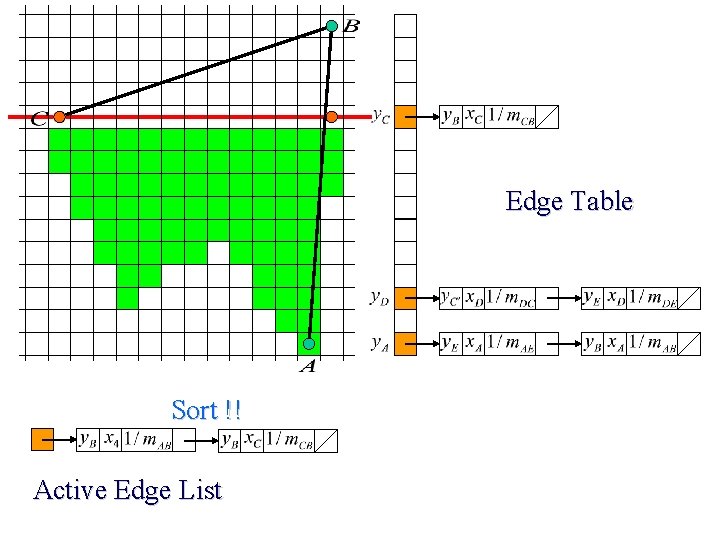
Edge Table Sort !! Active Edge List

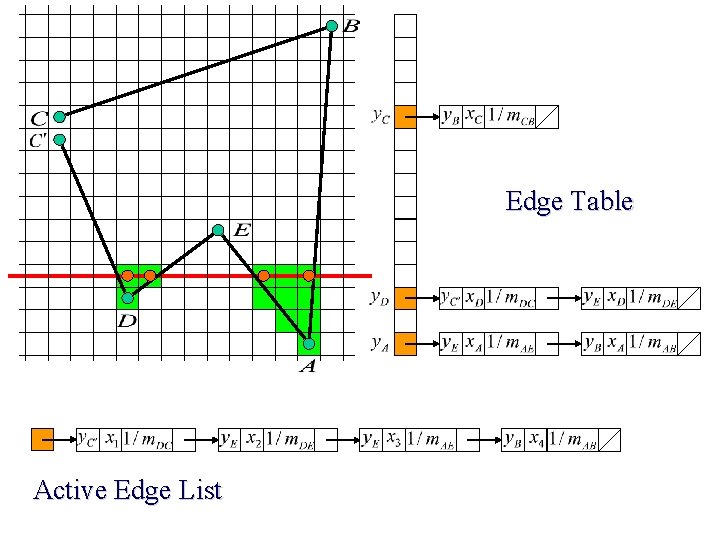
Edge Table Add & Sort !! Active Edge List

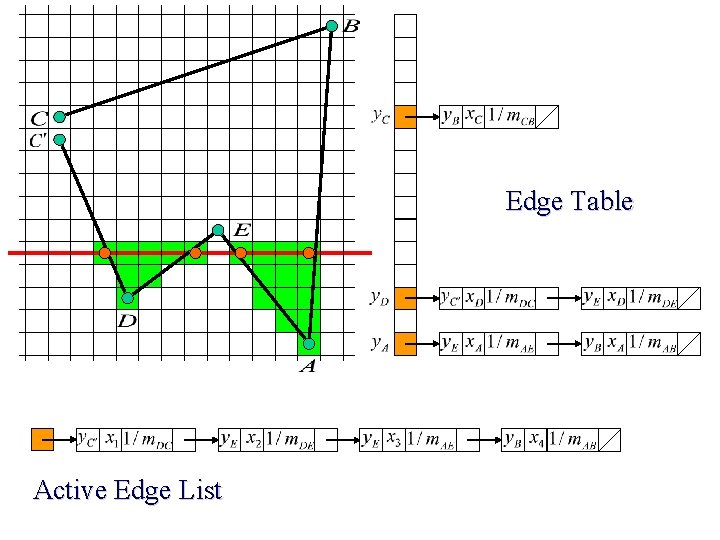
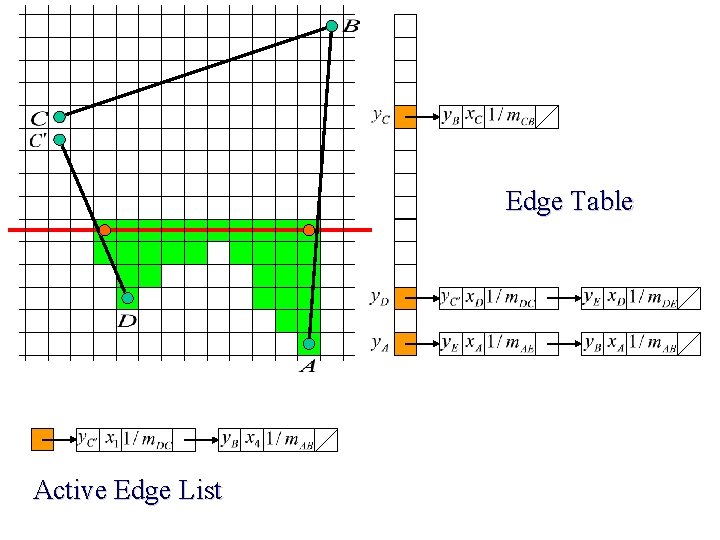
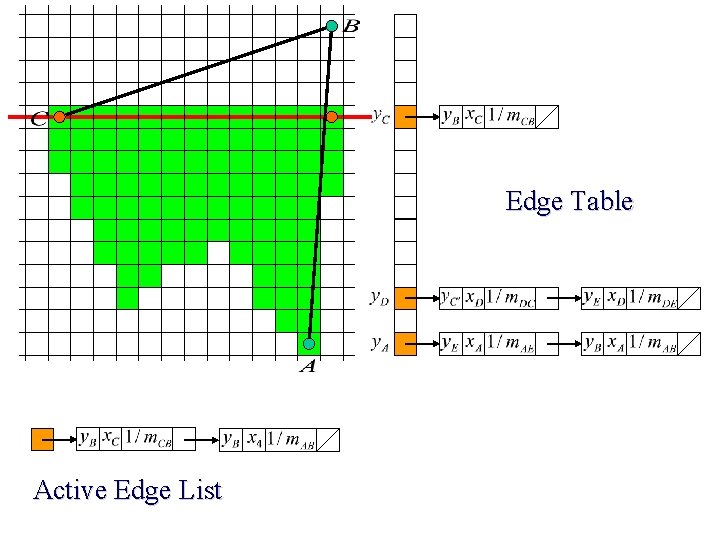
Edge Table Active Edge List

Edge Table Active Edge List

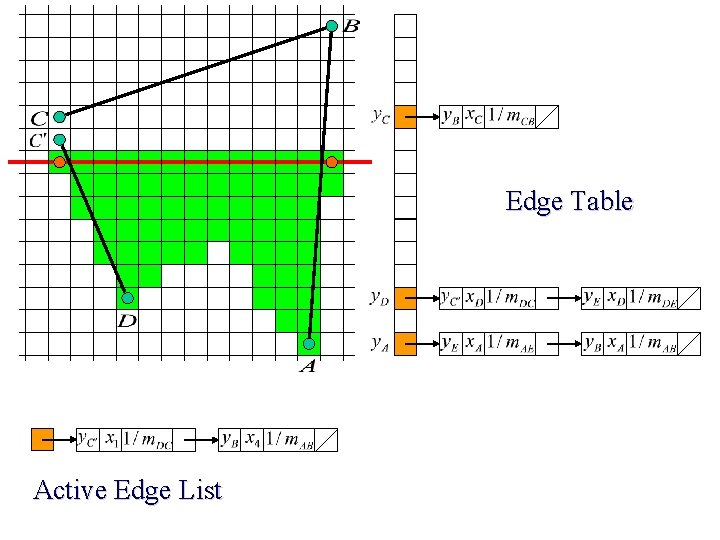
Edge Table Active Edge List

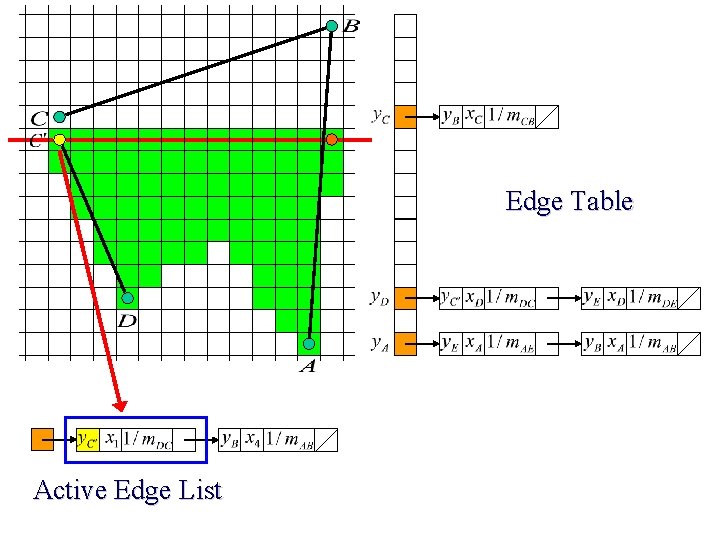
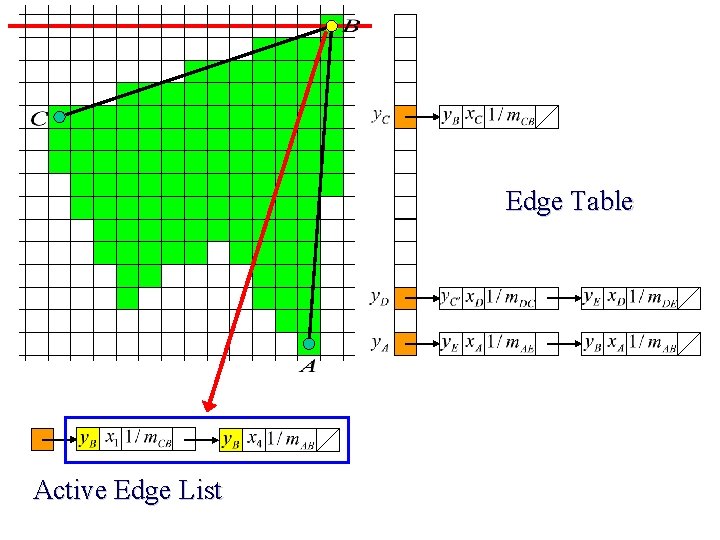
Edge Table Active Edge List

Edge Table Active Edge List

Edge Table Active Edge List

Edge Table Active Edge List

Edge Table Active Edge List

Edge Table Sort !! Active Edge List

Edge Table Active Edge List

Edge Table Active Edge List

Edge Table Empty Active Edge List

Scan Line Polygon Filling Construct the Edge Table (ET) excluding horizontal edge; Active Edge List (AEL) = null; for y = Ymin to Ymax Merge-sort ET[y] into AEL by x value Fill between pairs of x in AEL for each edge in AEL if edge. ymax = y remove edge from AEL else edge. x = edge. x + dx/dy sort AEL by x value end scan_fill

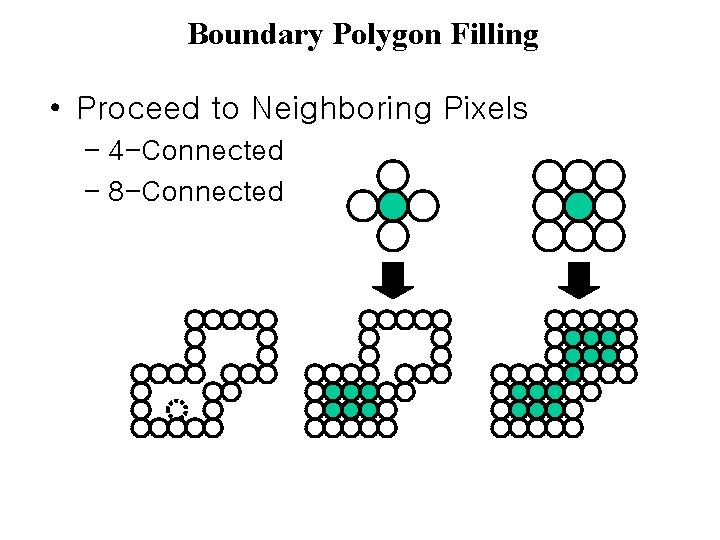
Boundary Polygon Filling • Proceed to Neighboring Pixels – 4 -Connected – 8 -Connected

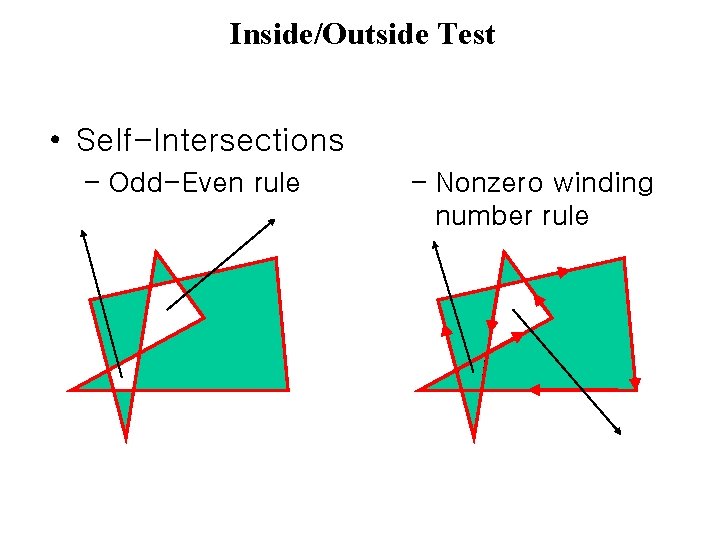
Inside/Outside Test • Self-Intersections – Odd-Even rule – Nonzero winding number rule

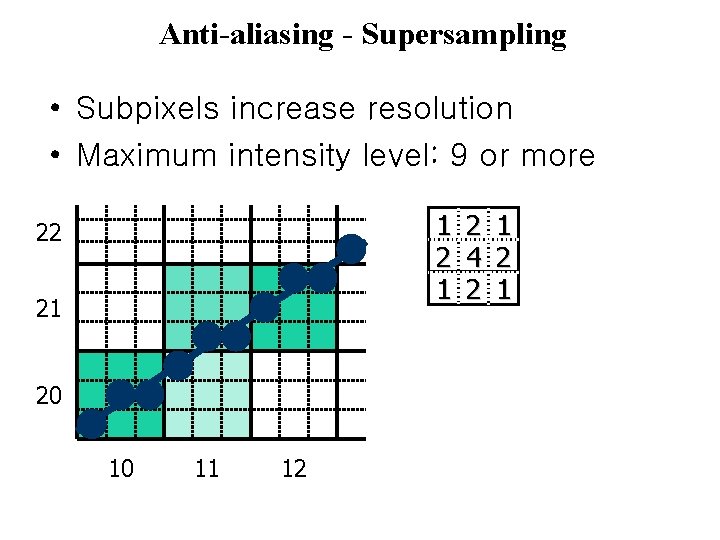
Anti-aliasing - Supersampling • Subpixels increase resolution • Maximum intensity level: 9 or more 1 22 21 20 10 11 12 2 4 2 1

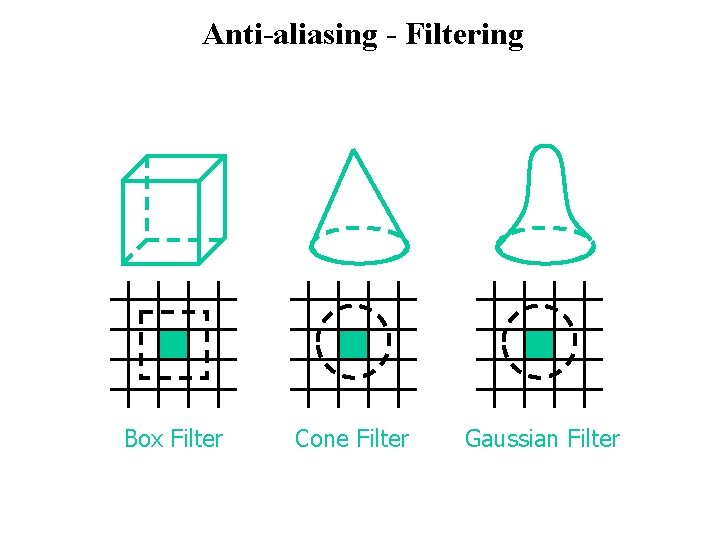
Anti-aliasing - Filtering Box Filter Cone Filter Gaussian Filter

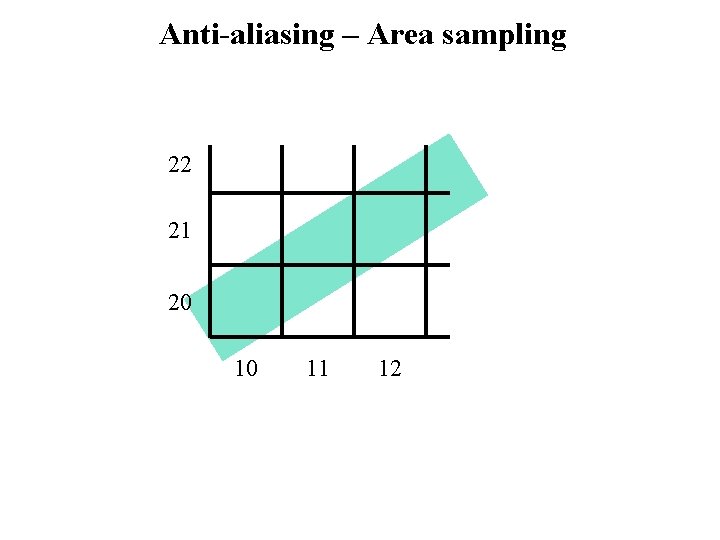
Anti-aliasing – Area sampling 22 21 20 10 11 12

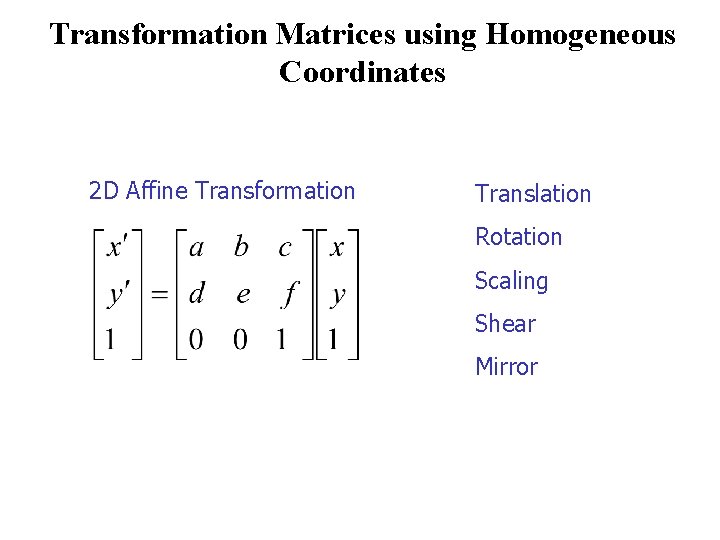
Transformation Matrices using Homogeneous Coordinates 2 D Affine Transformation Translation Rotation Scaling Shear Mirror

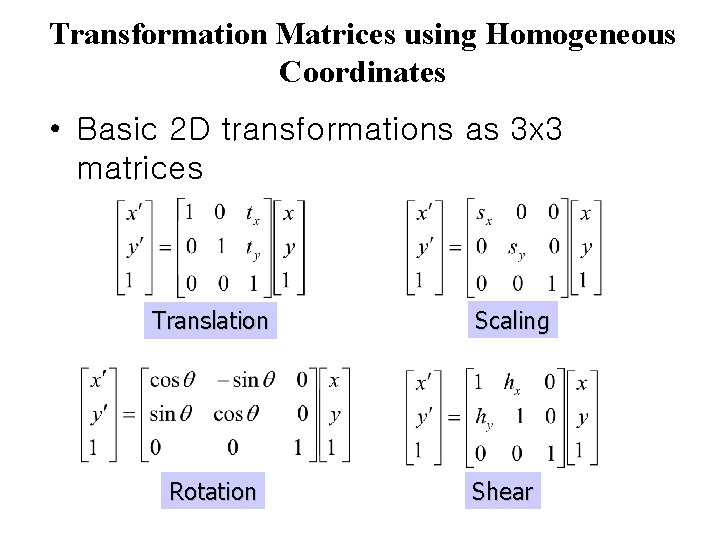
Transformation Matrices using Homogeneous Coordinates • Basic 2 D transformations as 3 x 3 matrices Translation Rotation Scaling Shear

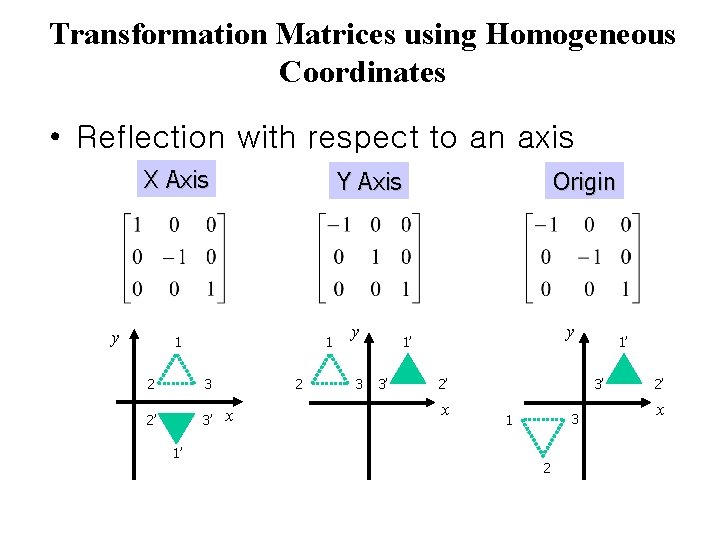
Transformation Matrices using Homogeneous Coordinates • Reflection with respect to an axis X Axis y Y Axis 1 1 2 3 2’ 3’ 1’ 2 x y 3 Origin y 1’ 3’ 2’ x 1’ 3’ 3 1 2 2’ x

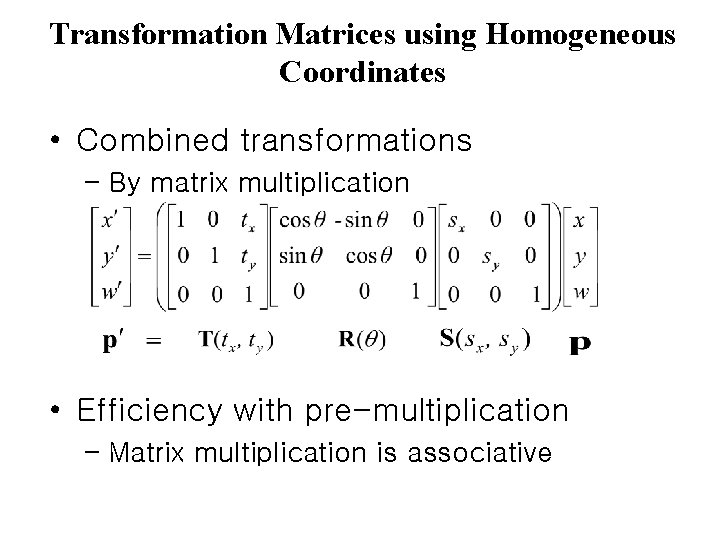
Transformation Matrices using Homogeneous Coordinates • Combined transformations – By matrix multiplication • Efficiency with pre-multiplication – Matrix multiplication is associative

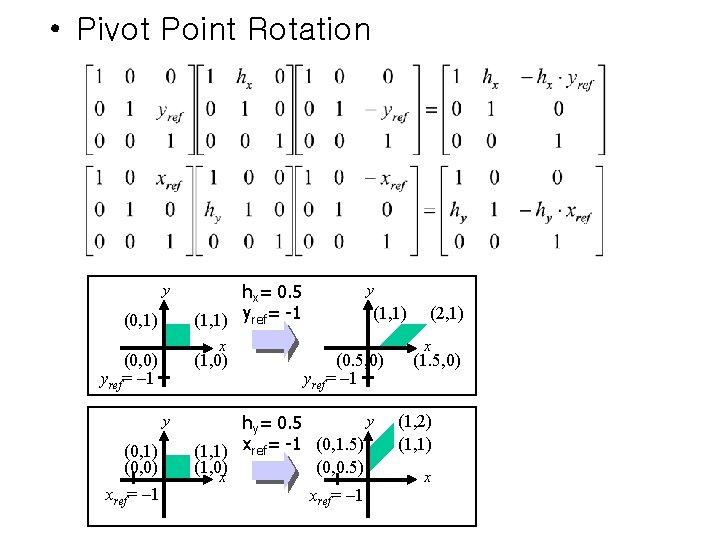
• Pivot Point Rotation • Fixed Point Scaling

• Pivot Point Rotation y (0, 1) x (0, 0) yref= – 1 (1, 0) y (0, 1) (0, 0) xref= – 1 hx= 0. 5 (1, 1) yref= -1 y (1, 1) (0. 5, 0) yref= – 1 y hy= 0. 5 (1, 1) xref= -1 (0, 1. 5) (0, 0. 5) (1, 0) x xref= – 1 (2, 1) x (1. 5, 0) (1, 2) (1, 1) x

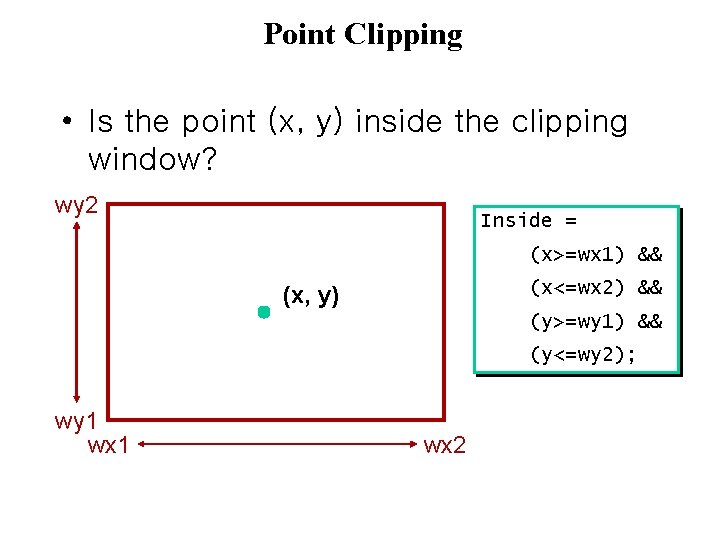
Point Clipping • Is the point (x, y) inside the clipping window? wy 2 Inside = (x>=wx 1) && (x<=wx 2) && (x, y) (y>=wy 1) && (y<=wy 2); wy 1 wx 2

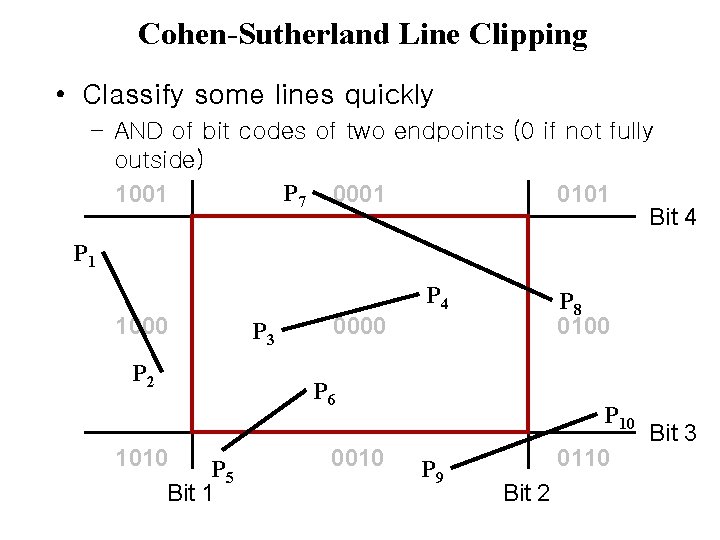
Cohen-Sutherland Line Clipping • Classify some lines quickly – AND of bit codes of two endpoints (0 if not fully outside) P 7 0001 1001 0101 Bit 4 P 1 P 4 1000 P 2 1010 P 5 Bit 1 P 3 P 8 0100 0000 P 6 0010 P 9 0110 Bit 2 Bit 3

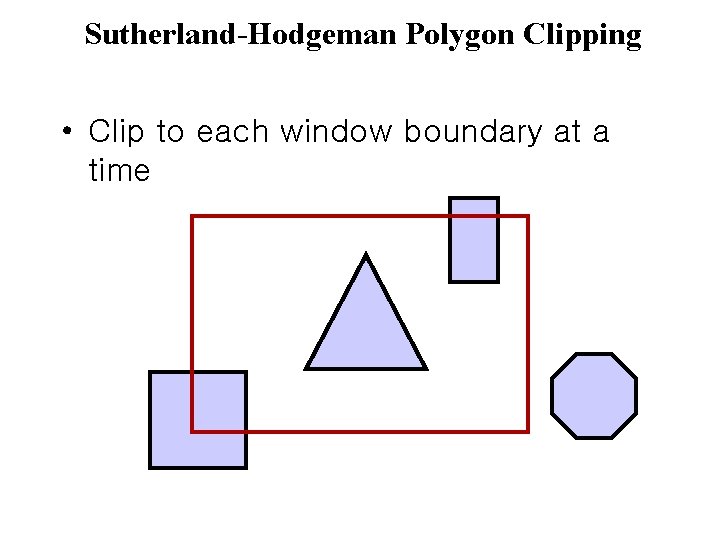
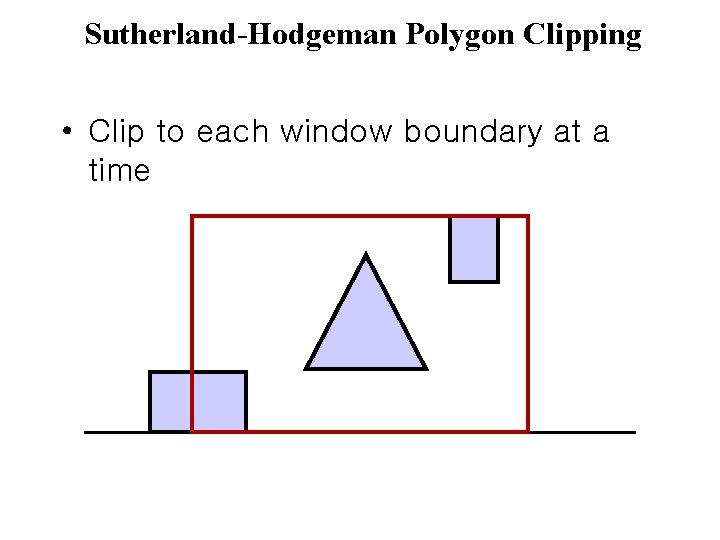
Sutherland-Hodgeman Polygon Clipping • Clip to each window boundary at a time

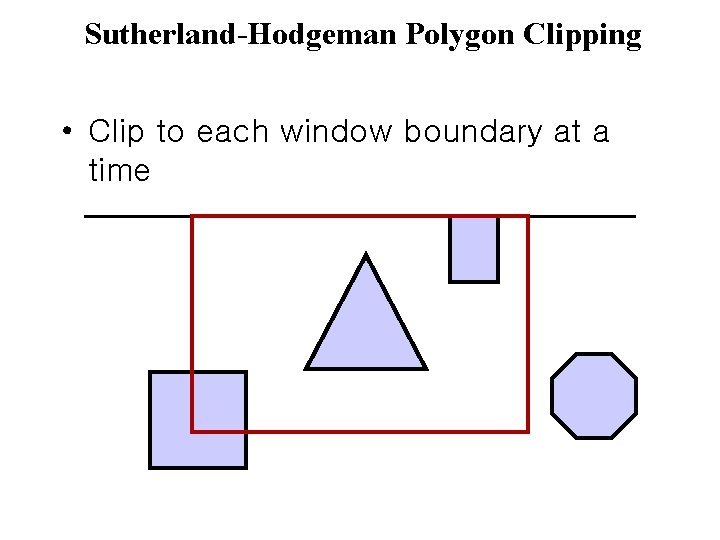
Sutherland-Hodgeman Polygon Clipping • Clip to each window boundary at a time

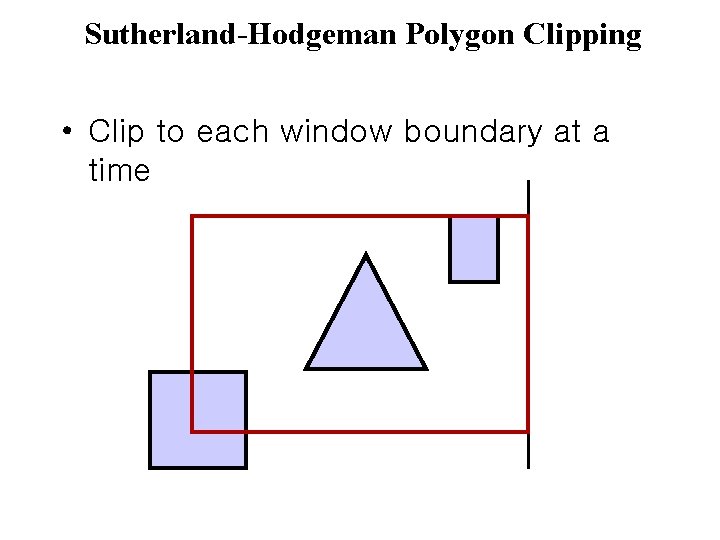
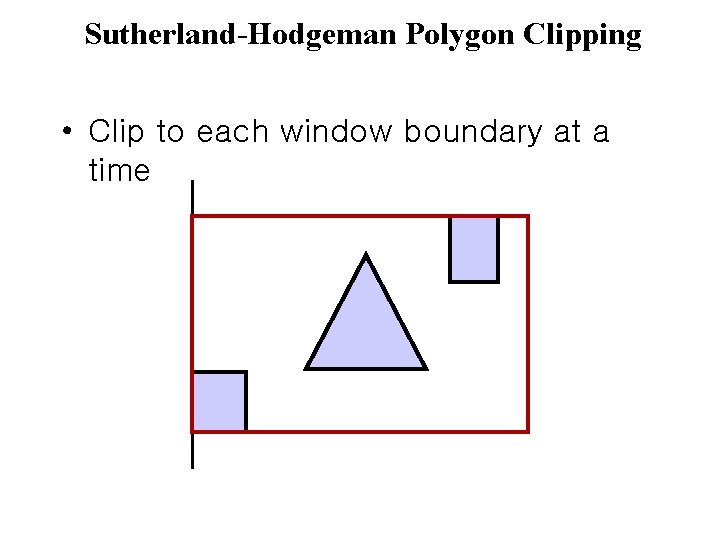
Sutherland-Hodgeman Polygon Clipping • Clip to each window boundary at a time

Sutherland-Hodgeman Polygon Clipping • Clip to each window boundary at a time

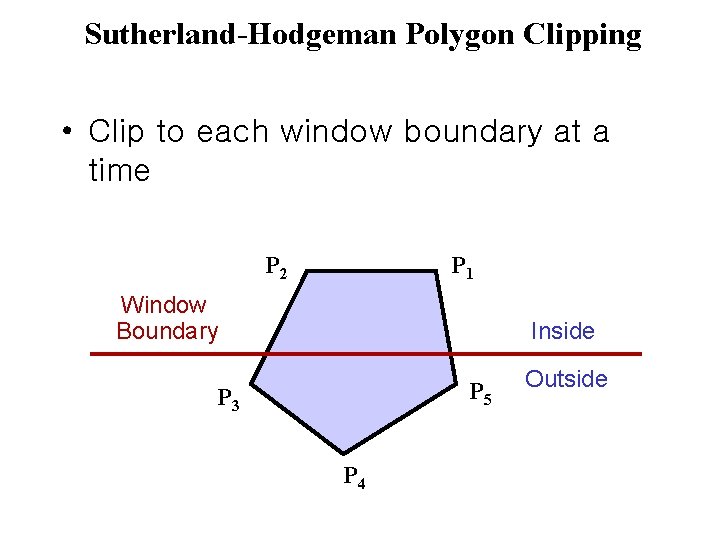
Sutherland-Hodgeman Polygon Clipping • Clip to each window boundary at a time

Sutherland-Hodgeman Polygon Clipping • Clip to each window boundary at a time P 2 P 1 Window Boundary Inside P 5 P 3 P 4 Outside

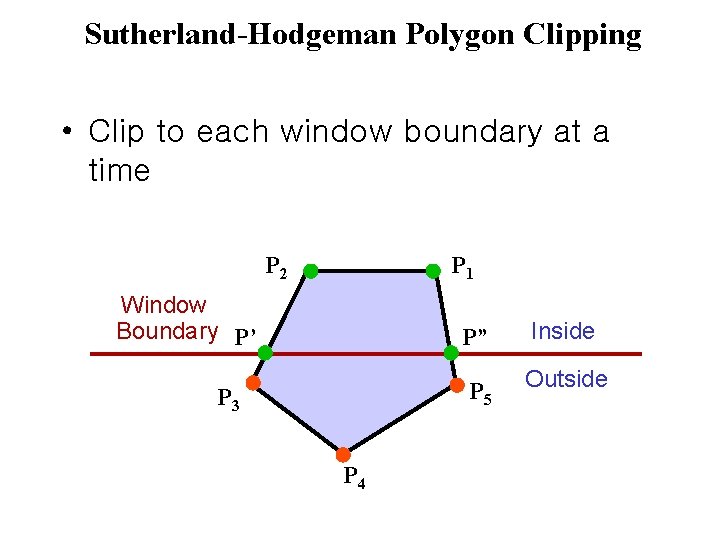
Sutherland-Hodgeman Polygon Clipping • Clip to each window boundary at a time P 2 P 1 Window Boundary P’ P” P 5 P 3 P 4 Inside Outside

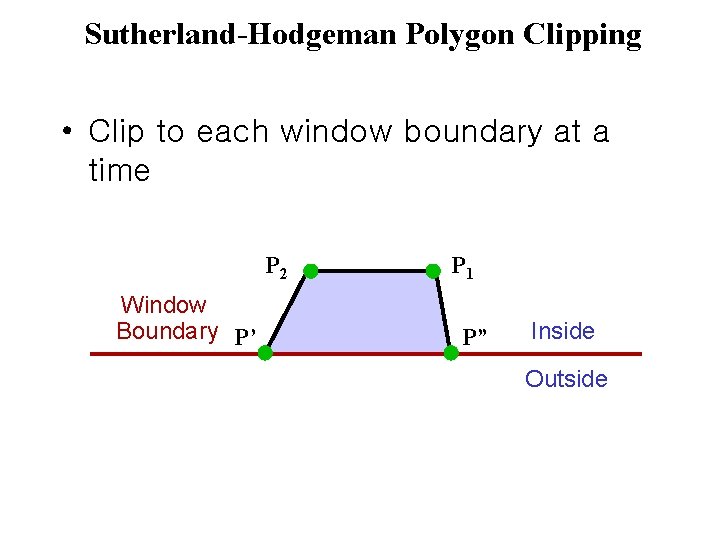
Sutherland-Hodgeman Polygon Clipping • Clip to each window boundary at a time P 2 Window Boundary P’ P 1 P” Inside Outside

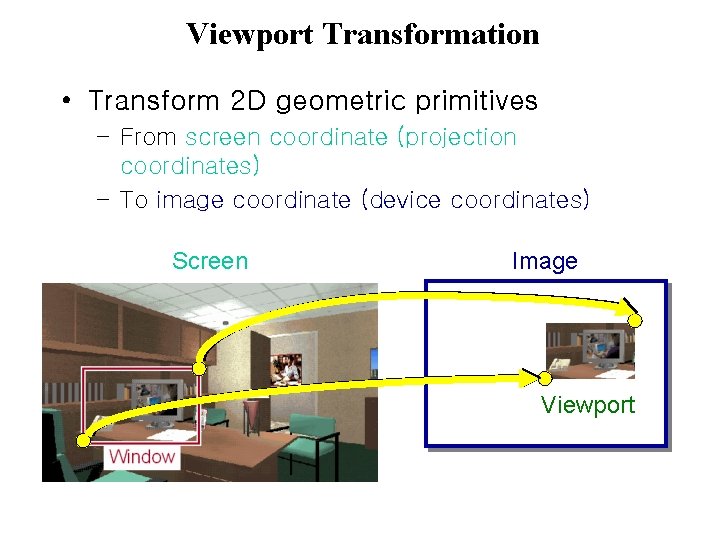
Viewport Transformation • Transform 2 D geometric primitives – From screen coordinate (projection coordinates) – To image coordinate (device coordinates) Screen Image Viewport

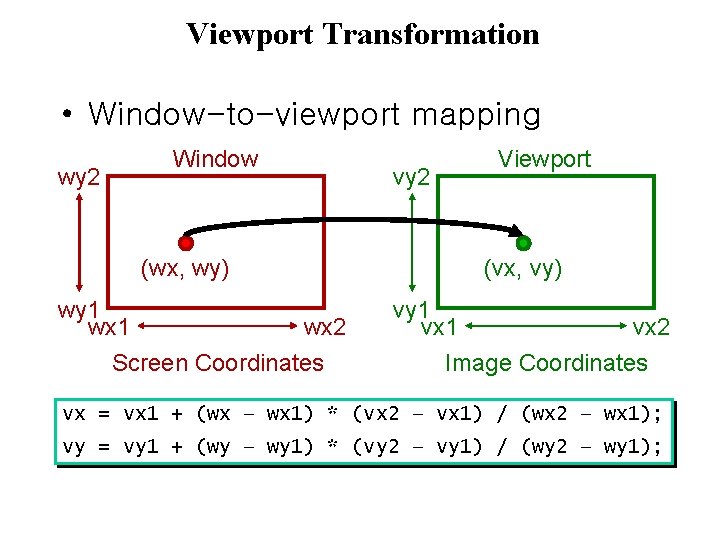
Viewport Transformation • Window-to-viewport mapping wy 2 Window (wx, wy) wy 1 wx 2 Screen Coordinates vy 2 Viewport (vx, vy) vy 1 vx 2 Image Coordinates vx = vx 1 + (wx – wx 1) * (vx 2 – vx 1) / (wx 2 – wx 1); vy = vy 1 + (wy – wy 1) * (vy 2 – vy 1) / (wy 2 – wy 1);