Notary Hardware Techniques to Enhance Signatures Luke Yen

Notary: Hardware Techniques to Enhance Signatures Luke Yen Collaborator: Prof. Stark C. Draper Advisor: Prof. Mark D. Hill University of Wisconsin, Madison MICRO-41 - November 11, 2008 www. cs. wisc. edu/multifacet/papers/micro 08_notary. pdf

Executive Summary Tackle 2 problems with hardware signatures: • Problem 1: Best signature hashing (i. e. , H 3) has high area & power overheads • Solution 1: Use entropy analysis to guide lower-cost hashing (Page-Block-XOR, PBX) that performs similar to H 3 – Ex: 160 gates for H 3 vs 20 gates for PBX • Problem 2: Spurious signature conflicts caused by signature bits set by private memory addrs • Solution 2: Avoid inserting private stack addrs, propose privatization interface for higher performance 6/7/2021 2 University of Wisconsin-Madison

Outline • Signature background • Entropy results & PBX • Privatization • Methodology & workloads • Results • Conclusions & Future Work 6/7/2021 3 University of Wisconsin-Madison

Signature background • Signatures (hardware Bloom filters) used to summarize and detect conflicts with a transaction’s read- and write-sets – Inspired by Bulk system [Ceze, ISCA’ 06] – Implemented in Log. TM-SE [Yen, HPCA’ 07] – Can have false positives, but never false negatives – Also proposed for non-TM purposes (e. g. , SC violation detection, atomicity violation detection, race recording) • Ex: Use k Bloom filters of size m/k, with independent hash functions 6/7/2021 4 University of Wisconsin-Madison

Signature hash functions • Which hash function is best? [Sanchez, MICRO’ 07] – Bit-selection? Hash simply decodes some number of input bits – H 3? Each bit of a hash value is an XOR of (on avg. ) half of the input address bits Log. TM-SE w/ 2 kb signatures • Result: H 3 better with >=2 hash functions • However, H 3 uses many multi-level XOR trees • Can we improve this? 6/7/2021 5 University of Wisconsin-Madison

H 3 implementation • Num XOR • Ex: 2 kb signatures, k=2, c=10, 32 -bit addr = 160 XOR gates per signature • Can we reduce the total gate count? 6/7/2021 6 University of Wisconsin-Madison

Outline • Signature background • Entropy results & PBX • Privatization • Methodology & workloads • Results • Conclusions & Future Work 6/7/2021 7 University of Wisconsin-Madison

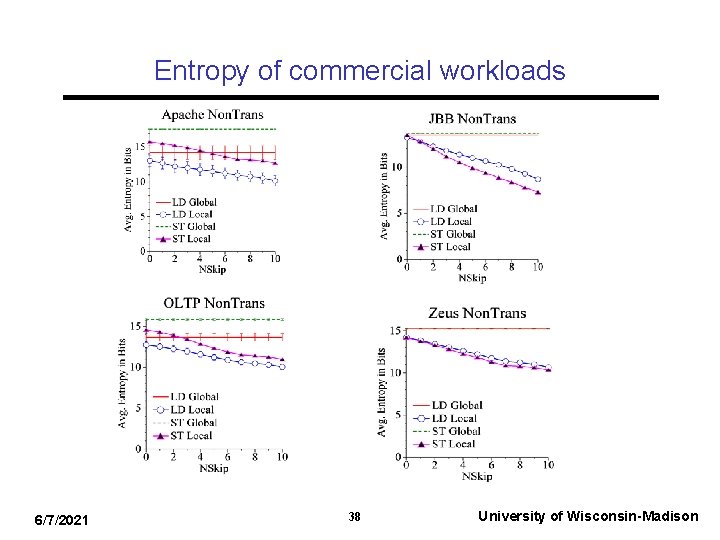
Entropy overview • Not all address bits have equal randomness – Ex: High-level address bits unlikely to change if working set size is small • Key insight: If input bits are random and those bits are used as inputs to hash functions, random hash values result – Use entropy to measure bit randomness • Entropy – measure of the uncertainty of a random variable x 6/7/2021 8 University of Wisconsin-Madison

Entropy formally defined • Entropy = • p(xi) = the probability of the occurrence of value xi • N = number of sample values random variable x can take on • Entropy = amount of information required on average to describe outcome of variable x (in bits) – Ex: What is the best possible lossless compression? 0 bits min Other cases Entropy value of n-bit field All bit patterns in n-bit field equally likely n-bit field has constant value 6/7/2021 n bits max 9 University of Wisconsin-Madison

Our measures of entropy • For our workloads, we care about: • Q 1: What is the best achievable entropy? – Global entropy – upper bound on entropy of address • Q 2: How does entropy change within an address? – Local entropy – entropy of bit-field within the address 31 Addr 6 31 Global entropy 6/7/2021 Local entropy 6 Addr NSkip 10 University of Wisconsin-Madison

Outline • Signature background • Entropy results & PBX • Privatization • Methodology & workloads • Results • Conclusions & Future Work 6/7/2021 11 University of Wisconsin-Madison

Entropy results • Workloads to be described later • Global entropy is at most 16 bits • Bit-window for local entropy is 16 bits wide (NSkip from 0 -10) – Smaller windows (<16 b) may not reach global entropy value – Larger windows (>16 b) hides some fine-grain info 6/7/2021 12 University of Wisconsin-Madison

Entropy results summary • More entropy results in our MICRO paper • In summary, for our workloads entropy monotonically decreases when moving towards high-order bits – We calculate the average entropy across the entire workload’s execution – May miss entropy changes due to program phase behavior • Our Page-Block-XOR (PBX) hash takes advantage of this overall trend 6/7/2021 13 University of Wisconsin-Madison

Page-Block-XOR (PBX) • Motivated by 3 findings: – (1) Lower-order bits have most entropy • Follows from our entropy results – (2) XORing two bit-fields produces random hash values • From prior work on XOR hashing (e. g. , data placement in caches, DRAM) – (3) Bit-field overlaps can lead to higher false positives • Correlation between the two bit-fields can reduce the range of hash values produced (worse for larger signatures) 6/7/2021 14 University of Wisconsin-Madison

PBX implementation • For 2 kb signatures with 2 hash functions: – 20 XOR gates for PBX vs 160 XOR gates for H 3! • PPN and Cache-index fields not tied to system params: • Use entropy to find two non-overlapping bit-fields with high randomness 6/7/2021 15 University of Wisconsin-Madison

Summary thus far • Problem 1: H 3 has high area & power overheads • Solution 1: Use entropy analysis to guide lower-cost PBX – Ex: 160 gates for H 3 vs 20 gates for PBX • Problem 2: Spurious signature conflicts caused by signature bits set by private memory addrs • Solution 2: To be described 6/7/2021 16 University of Wisconsin-Madison

Outline • Signature background • Entropy results & PBX • Privatization • Methodology & workloads • Results • Conclusions & Future Work 6/7/2021 17 University of Wisconsin-Madison

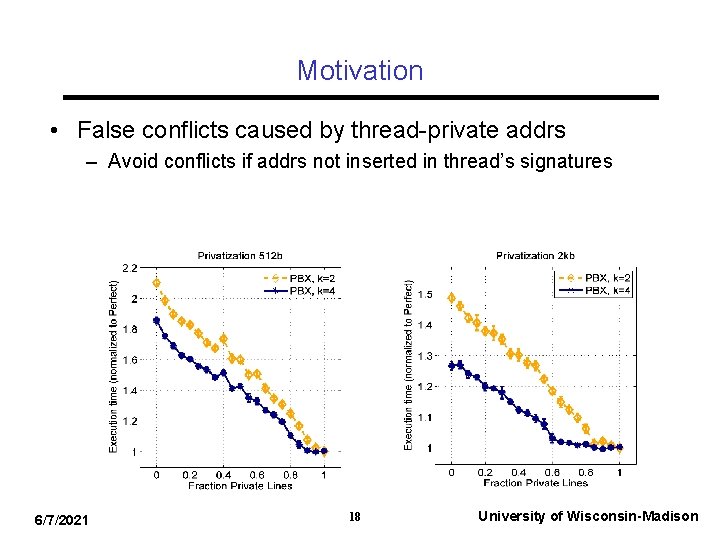
Motivation • False conflicts caused by thread-private addrs – Avoid conflicts if addrs not inserted in thread’s signatures 6/7/2021 18 University of Wisconsin-Madison

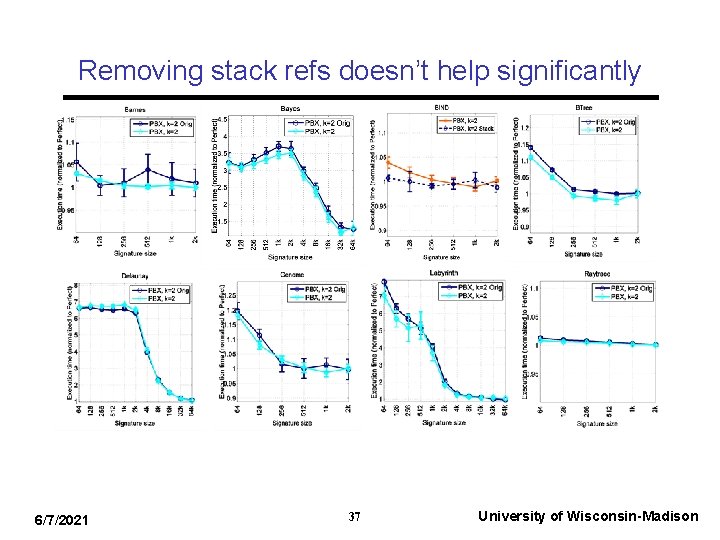
Privatization solutions • Two solutions proposed: – (1) Remove private stack references from sigs. • Very little work for programmer/compiler • Benefits depend on fraction of stack addresses versus all transactional references – (2) Language-level interface (e. g. , private_malloc(), shared_malloc()) • Even higher performance boost • For skilled programmer • WARNING: Incorrectly marking shared objects as private can lead to program errors! 6/7/2021 19 University of Wisconsin-Madison

Page-based implementation • Each page is assigned a status, private or shared – Invariant: Page is shared if any object is shared • If stack is private, library marks stack pages as private • If using privatization heap functions, mark heap pages accordingly 6/7/2021 20 University of Wisconsin-Madison

OS support • OS allocates different physical page frames for shared and private pages – Sets a per-frame bit in translation entry if shared – Reduce number of page frames used by packing objects with same status together • Signatures insert memory addresses of transactional references to shared pages – Query page sharing bit in HW TLB & current transactional status 6/7/2021 21 University of Wisconsin-Madison

Outline • Signature background • Entropy results & PBX • Privatization • Methodology & workloads • Results • Conclusions & Future Work 6/7/2021 22 University of Wisconsin-Madison

Methodology • Full-system simulation using Simics and Wisconsin GEMS timing modules • Transistor-level design for area & power of XOR gates • CACTI for Bloom filter bit array area & power • Simulated system – – – 6/7/2021 Single-chip CMP 16 single-threaded, in-order cores 32 k. B, 4 -way private L 1 I & D, write-back 8 MB, 8 -way shared L 2 cache MESI directory protocol Signatures from 64 b-64 kb (8 B-8 k. B) & “Perfect” 23 University of Wisconsin-Madison

Workloads • Micro-benchmarks – BTree – read and write ops on shared tree – Sparse Matrix – algorithm from dense column vector multiplication kernel • SPLASH-2 apps – Barnes & Raytrace – exert most signature pressure • Stanford STAMP apps – Vacation, Genome, Delaunay, Bayes, Labyrinth • DNS server – BIND 6/7/2021 24 University of Wisconsin-Madison

Outline • Signature background • Entropy results & PBX • Privatization • Methodology & workloads • Results • Conclusions & Future Work 6/7/2021 25 University of Wisconsin-Madison

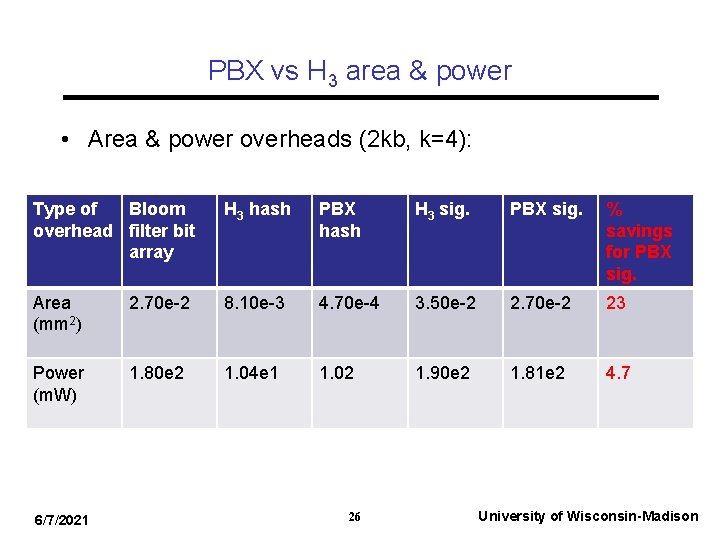
PBX vs H 3 area & power • Area & power overheads (2 kb, k=4): Type of Bloom overhead filter bit array H 3 hash PBX hash H 3 sig. PBX sig. % savings for PBX sig. Area (mm 2) 2. 70 e-2 8. 10 e-3 4. 70 e-4 3. 50 e-2 2. 70 e-2 23 Power (m. W) 1. 80 e 2 1. 04 e 1 1. 02 1. 90 e 2 1. 81 e 2 4. 7 6/7/2021 26 University of Wisconsin-Madison

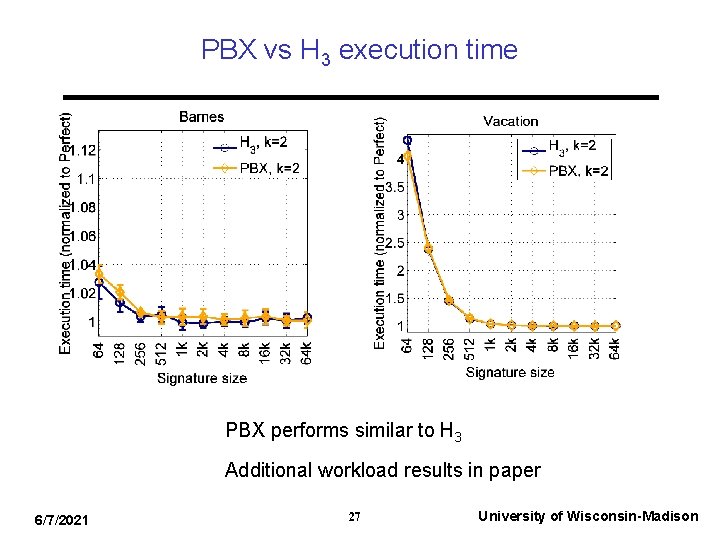
PBX vs H 3 execution time PBX performs similar to H 3 Additional workload results in paper 6/7/2021 27 University of Wisconsin-Madison

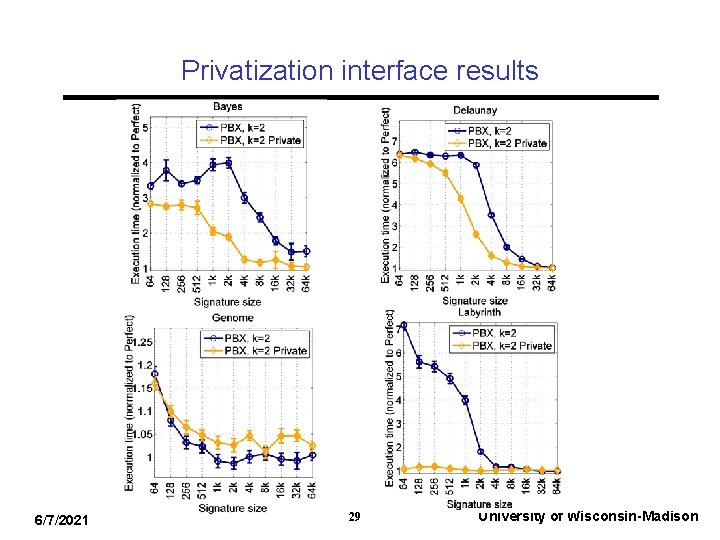
Privatization results summary • Removing private stack references from signatures did not help much – Most addr references not to stack – Most likely because running with SPARC ISA. Other ISAs (e. g. , x 86) likely has more benefits • Privatization interface helps four workloads – Remainder either does not have private heap structures or does not have high transactional duty cycle 6/7/2021 28 University of Wisconsin-Madison

Privatization interface results 6/7/2021 29 University of Wisconsin-Madison

Outline • Signature background • Entropy results & PBX • Privatization • Methodology & workloads • Results • Conclusions & Future Work 6/7/2021 30 University of Wisconsin-Madison

Conclusions • Tackle 2 problems with signature designs: – (1) Area and power overheads of H 3 hashing • E. g. , 160 XOR gates for H 3, 20 for PBX – (2) False conflicts due to signature bits set by private memory references • Our solutions: – (1) Use entropy analysis to guide hashing function (PBX), a low-cost alternative that performs similarly to H 3 – (2) Prevent private stack references from entering signatures, and propose a privatization interface for heap allocations • Notary can be applied to non-TM uses: – PBX hashing can directly transfer – Privatization may transfer if addr filtering applies 6/7/2021 31 University of Wisconsin-Madison

Future Work • Dynamic entropy calculation: – How to adapt PBX hashing to entropy changes over time? • Dynamic privatization characteristics: – How common is it for objects to change sharing status (i. e. , from private to shared, and vice versa)? 6/7/2021 32 University of Wisconsin-Madison

BACKUP SLIDES 6/7/2021 33 University of Wisconsin-Madison

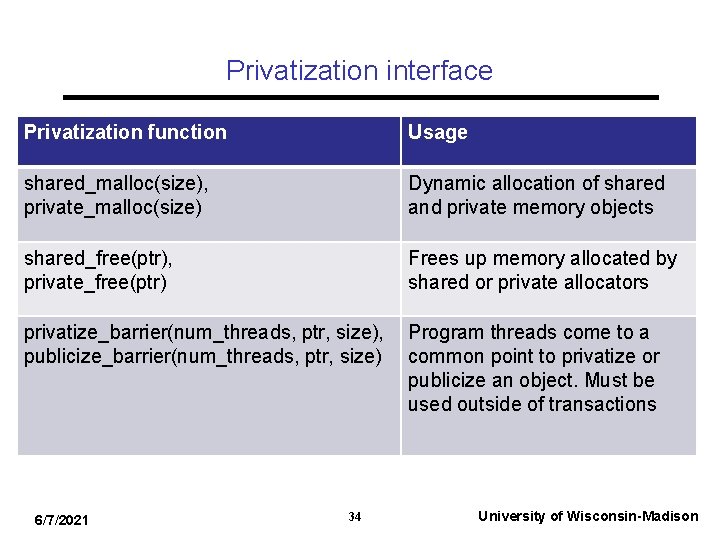
Privatization interface Privatization function Usage shared_malloc(size), private_malloc(size) Dynamic allocation of shared and private memory objects shared_free(ptr), private_free(ptr) Frees up memory allocated by shared or private allocators privatize_barrier(num_threads, ptr, size), publicize_barrier(num_threads, ptr, size) Program threads come to a common point to privatize or publicize an object. Must be used outside of transactions 6/7/2021 34 University of Wisconsin-Madison

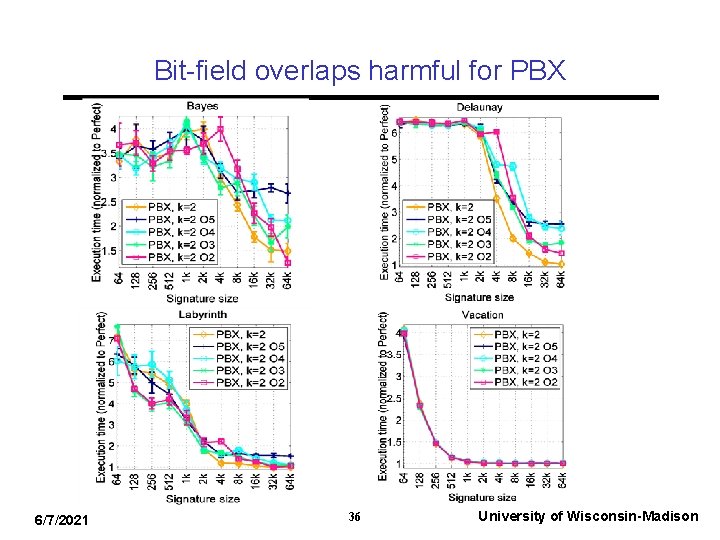
Dynamic privatization • Dynamically switch from private to shared, and vice versa • If transitioning from private -> shared, safe to mark page as shared (at cost of performance) • If transitioning from shared -> private, default policy is to disallow if there exists other shared objects on same page • Otherwise, trap to user software and let programmer call shared_free(), followed by private_malloc() on object 6/7/2021 35 University of Wisconsin-Madison

Bit-field overlaps harmful for PBX 6/7/2021 36 University of Wisconsin-Madison

Removing stack refs doesn’t help significantly 6/7/2021 37 University of Wisconsin-Madison

Entropy of commercial workloads 6/7/2021 38 University of Wisconsin-Madison

Signature Operation Example Program: xbegin LD A ST B LD C LD D ST C … 6/7/2021 External F A C D ST E B Hash Function(s) R 00100100 00000000 W 0010 00000010 39 ALIAS FALSE POSITIVE: NO CONFLICT! University of Wisconsin-Madison

Type of Hash Functions • In real programs, addresses neither independent nor uniformly distributed (key assumptions to derive PFP(n)) • But can generate hash values that are almost uniformly distributed and uncorrelated with good (universal/almost universal) hash functions • Hash functions considered: Bit-selection H 3 [Carter, CSS 79] (moderate, higher quality) (inexpensive, low quality) 6/7/2021 40 University of Wisconsin-Madison