NOSTALGIA v Hukum I Newton F 0 berlaku


NOSTALGIA v Hukum I Newton: ∑F = 0 berlaku untuk benda yang: a. diam b. GLB v Hukum II Newton: ∑F = ma berlaku untuk benda yang: GLBB v Hukum III Newton: Faksi = - Freaksi syarat: a. terjadi pada dua benda b. dua gaya yang bekerja pada benda sama besar tetapi arahnya berlawanan.

Gesekan • Gaya gesekan antar permukaan zat padat merupakan gaya sentuh, yang muncul jika permukaan dua zat padat bersentuhan secara fisik, dengan arah gaya gesekan sejajar dengan permukaan bidang sentuh dan berlawanan dengan kecenderungan arah gerak relatif benda satu terhadap benda lainnya.
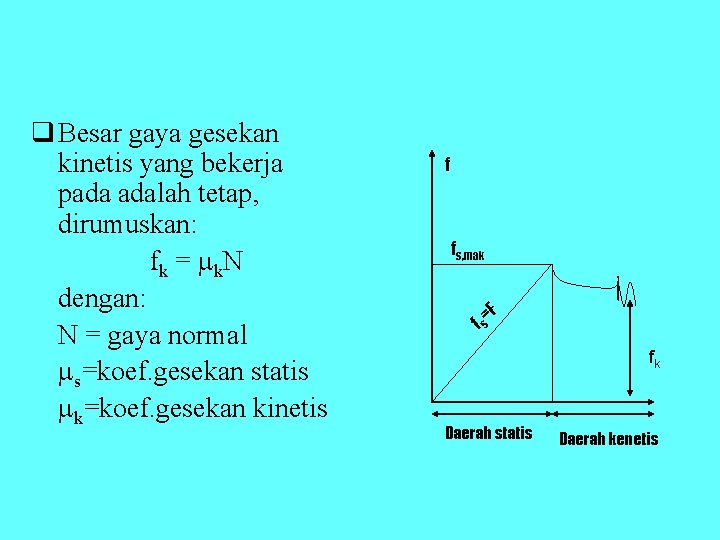
q Besar gaya gesekan kinetis yang bekerja pada adalah tetap, dirumuskan: f k = k. N dengan: N = gaya normal s=koef. gesekan statis k=koef. gesekan kinetis f fs, mak F = fs fk Daerah statis Daerah kenetis
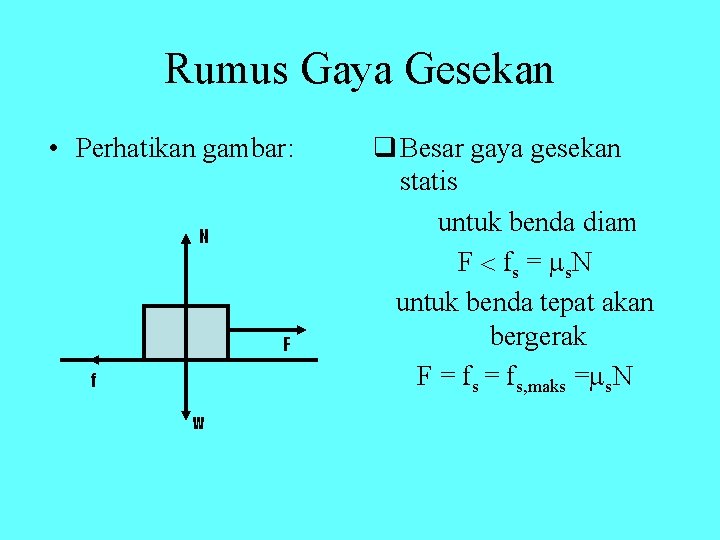
Rumus Gaya Gesekan • Perhatikan gambar: N F f w q Besar gaya gesekan statis untuk benda diam F fs = s N untuk benda tepat akan bergerak F = fs, maks = s. N

Contoh: • Sebuah balok kayu bermassa 4 kg diletakkan di atas meja kasar (lihat gambar). Percepatan gravitasi 10 m/s 2 dan koefisien gesekan antara permukaan meja dan balok 0, 2 dan 0, 4. • Berapakah besar gaya gesekan jika balok itu ditarik dengan gaya F yang besarnya: a. 6 N, • b. 16 N , c. 20 N F
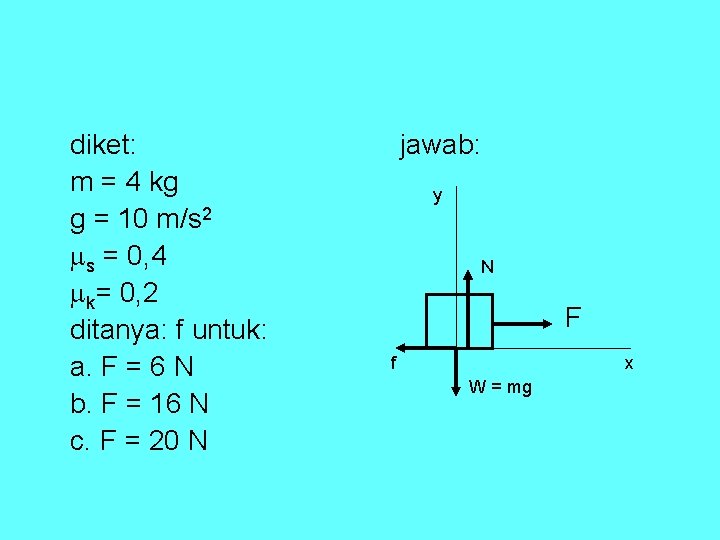
diket: m = 4 kg g = 10 m/s 2 s = 0, 4 k= 0, 2 ditanya: f untuk: a. F = 6 N b. F = 16 N c. F = 20 N jawab: y N F f x W = mg

pada sumbu y: ∑Fy = 0 N – mg = 0 N = mg N = 4 x 10 N = 40 newton Gaya gesek statis maksimum: fs, maks= s. N fs, maks= (0, 4)(40) = 16 newton a. F = 6 N. Tampak bahwa F fs, maks sehingga balok tidak bergerak. Maka fs = F = 6 N

b. F = 16 N. Tampak bahwa F = fs, maks sehingga balok tepat akan bergerak. Maka: ∑Fx = 0 fs = F = 16 N c. F = 20 N Tampak bahwa F fs, maks sehingga balok bergerak. Maka gaya gesekkannya gaya gesek kinetis, yaitu: f k = k. N = (0, 2)(40) =8 N Untuk percepatan balok dapat dihitung: ∑Fx = max F – fk = max ax = 3 m/s 2
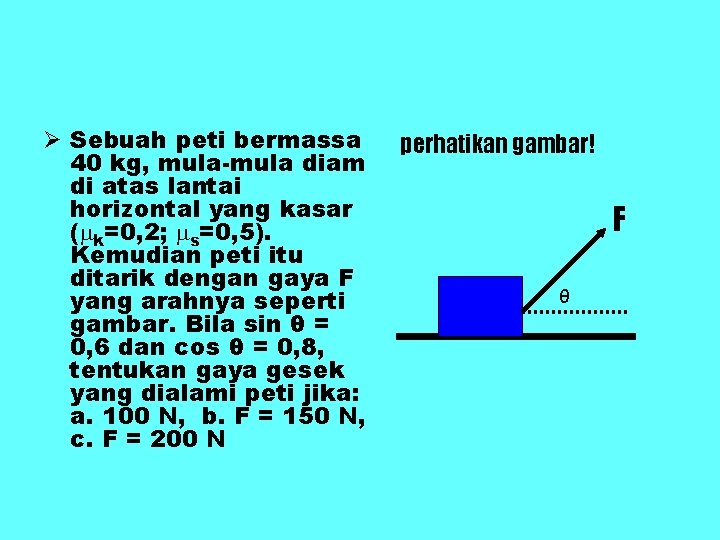
Ø Sebuah peti bermassa 40 kg, mula-mula diam di atas lantai horizontal yang kasar ( k=0, 2; s=0, 5). Kemudian peti itu ditarik dengan gaya F yang arahnya seperti gambar. Bila sin θ = 0, 6 dan cos θ = 0, 8, tentukan gaya gesek yang dialami peti jika: a. 100 N, b. F = 150 N, c. F = 200 N perhatikan gambar! F θ
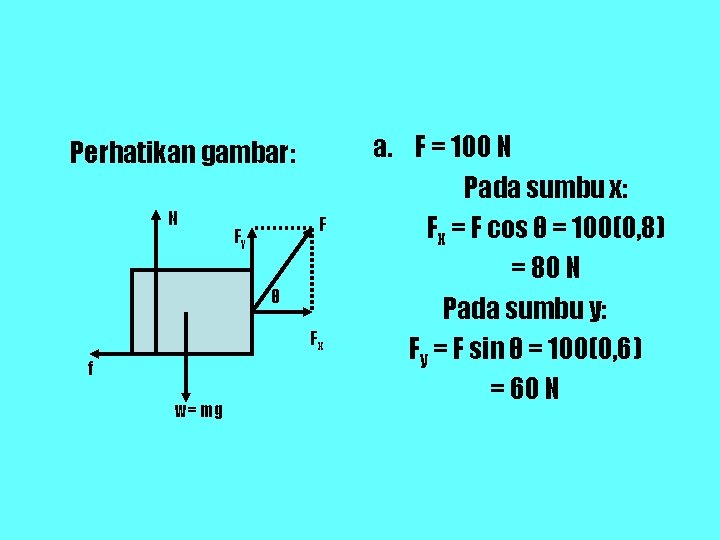
Perhatikan gambar: N F Fy θ Fx f w= mg a. F = 100 N Pada sumbu x: Fx = F cos θ = 100(0, 8) = 80 N Pada sumbu y: Fy = F sin θ = 100(0, 6) = 60 N

karena peti diam terhadap sumbu y, maka berlaku: ∑Fy= 0 N + Fy – mg = 0 N = mg – Fy = 40(10) – 60 = 400 – 60 N = 340 N fs, maks = s. N = 0, 5(340) = 170 N f k = k. N = 0, 2(340) = 68 N Karena Fx fs, maks berarti benda belum bergerak atau diam, maka:

b. gaya gesek statis yang dialami benda adalah: fs = Fx = 80 N F = 150 N Fx = F cos θ = 150(0, 8) = 120 N Fy = F sin θ = 150 (0, 6) = 90 N ∑Fy= 0 N + Fy – mg = 0 N = mg – Fy = 40(10) – 90 = 400 – 90 N = 310 N fs, maks = s. N = 0, 5(310) = 155 N F k = k. N = 0, 2(310) = 62 N

c. karena Fx fs, maks maka peti tetap diam, sehingga gaya gesek yang bekerja pada peti sebesar: fs = Fx = 120 N F = 200 N Fx = F cos θ = 200 (0, 8) = 160 N Fy = F sin θ = 200(0, 6) = 120 N ∑Fy= 0 N + Fy – mg = 0 N = mg – Fy = 400 – 120 N = 280 N fs, maks = s. N = 0, 5(280) =140 N f k = k. N = 0, 2(280) = 56 N

karena Fx fs, maks maka peti akan bergerak, sehingga gaya gesek yang bekerja pada peti sebesar: fk = 56 N percepatan peti: ∑Fx = max Fx – fk = max

Ø Penghapus papan tulis yang beratnya 0, 8 N dipakai untuk menghapus papan tulis yang letaknya vertikal. Siswa yang menggunakan peghapus tadi menekannya tegak lurus ke papan tulis dengan gaya 10 N. Bila koefisien gesekan kinetik antara penghapus dan papan tulis adalah 0, 4 maka untuk menggerakkan dengan kecepatan tetap, siswa tadi harus menariknya dengan gaya……. . newton.
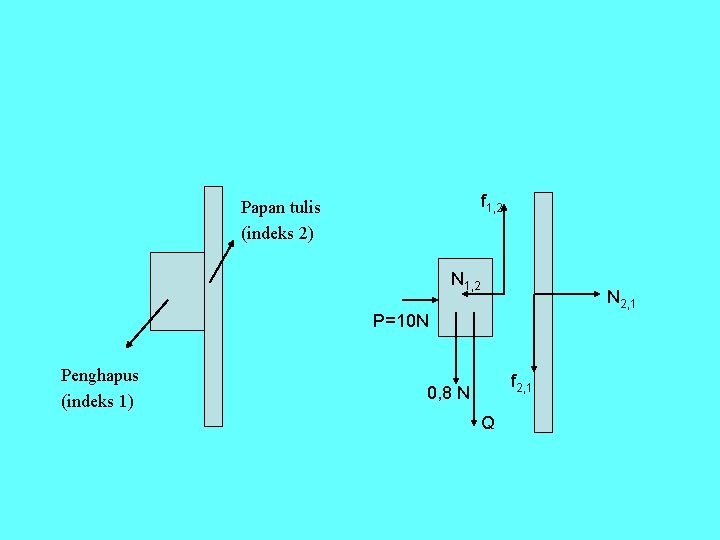
f 1, 2 Papan tulis (indeks 2) N 1, 2 N 2, 1 P=10 N Penghapus (indeks 1) f 2, 1 0, 8 N Q

Penyelesaian: Penghapus tidak bergerak dalam arah sumbu x, sehingga: ∑Fx = 0 P – N 1, 2 = 0 P = N 1, 2= 10 N maka gaya gesek kinetik: f 1, 2 = k. N 1, 2 = (0, 4)10 = 4 newton Penghapus bergerak dengan kecepatan tetap pada arah sumbu y, sehingga: ∑Fy = 0 0, 8 + Q – f 1, 2 = 0 Q = f 1, 2 – 0, 8 Q = 4 – 0, 8 Q = 3, 2 newton
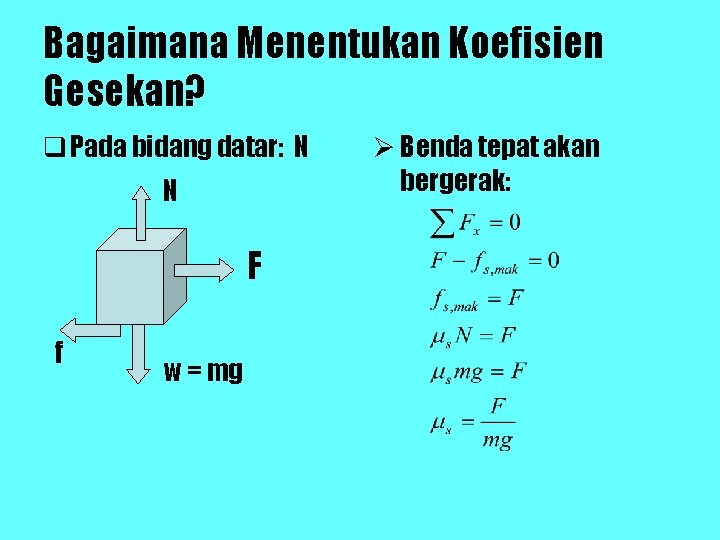
Bagaimana Menentukan Koefisien Gesekan? q Pada bidang datar: N N F f w = mg Ø Benda tepat akan bergerak:

Ø Benda bergerak dengan kecepatan konstan (a = 0)

Uji Kemampuan • Sebuah peti 25 kg diam pada sebuah lantai dasar kasar. Gaye horizontal 80 N diperlukan untuk mengusahakan agar peti itu tepat akan bergerak. Setelah peti bergerak, hanya diperlukan gaya 60 N untuk menjaga agar peti bergerak dengan kecepatan konstan. Hitunglah koefisien gesekan statis dan kinetis antara peti dan lantai.
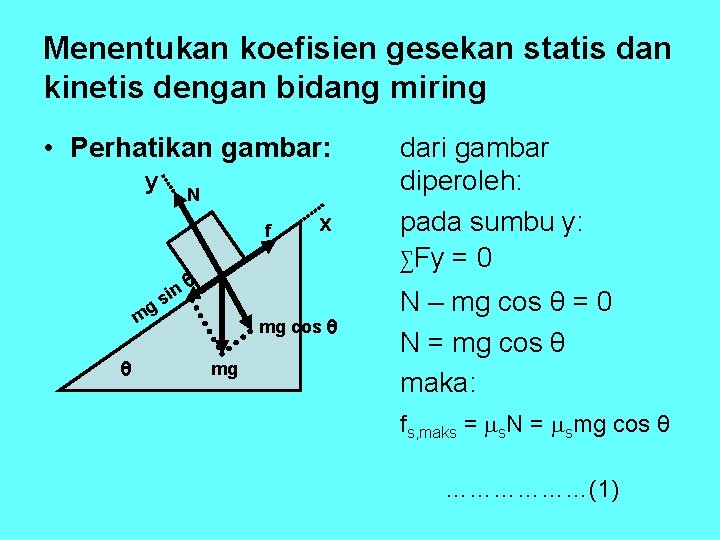
Menentukan koefisien gesekan statis dan kinetis dengan bidang miring • Perhatikan gambar: y N f g m θ sin x θ mg cos θ mg dari gambar diperoleh: pada sumbu y: ∑Fy = 0 N – mg cos θ = 0 N = mg cos θ maka: fs, maks = s. N = smg cos θ ………………(1)

untuk benda tepat akan bergerak: ∑Fx = 0 mg sin θ – fs, mak= 0 mg sin θ = fs, mak. . . (2) pers (1) di maksukan ke pers (2) diperoleh: mg sin θ = smg cos θ maka: dengan cara yang sama diperoleh: (bergerak dengan kecepatan tetap) k = tan θk

Uji Kemampuan • Seorang siswa ingin menentukan koefisien gesekan antara karet dan suatu permukaan benda. Untuk itu dia menyiapkan sebuah penghapus karet dan perm ukaan bidang miring. Pada percobaan pertama, dia menaruh penghapus karet di atas bidang dan memperbesar kemiringan bidang sedikit demi sedikit. Dia mendapatkan bahwa penghapus tepat akan meluncur ke bawah bidang jika sudut kemiringan bidang 370 terhadap arah horizontal ( sin 370 = 0, 6). Begitu penghapus bergerak hanya diperlukan kemiringan 300 agar penghapus bergerak dengan kecepatan tetap 6 m/s. Dari data-data itu, tentukan koefisien gesekan statis dan kinetis antara permukaan bidang dengan karet.
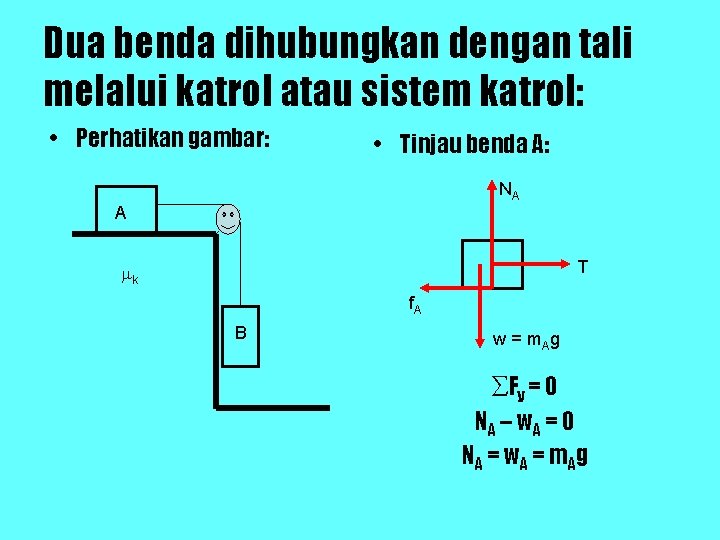
Dua benda dihubungkan dengan tali melalui katrol atau sistem katrol: • Perhatikan gambar: • Tinjau benda A: NA A T k f. A B w = m. Ag ∑Fy = 0 NA – w. A = 0 NA = w. A = m Ag
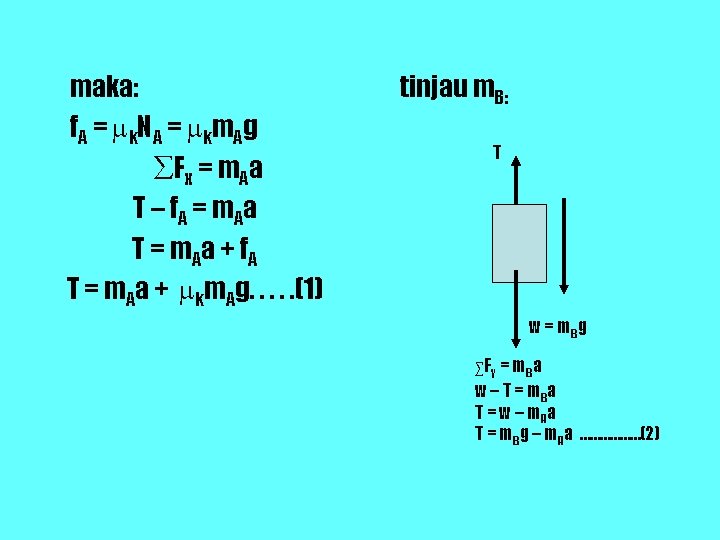
maka: f A = k. N A = km A g ∑Fx = m. Aa T – f. A = m A a T = m A a + f. A T = m. Aa + km. Ag. . . (1) tinjau m. B: T w = m. Bg ∑Fy = m. Ba w – T = m. Ba T = w – m. Aa T = m. Bg – m. Aa ………………(2)

pers (1) = (2) didapat: m A a + km A g = m B g – m B a m A a + m B a = m B g - km A g a (m. A + m. B) = g(m. B - km. A)
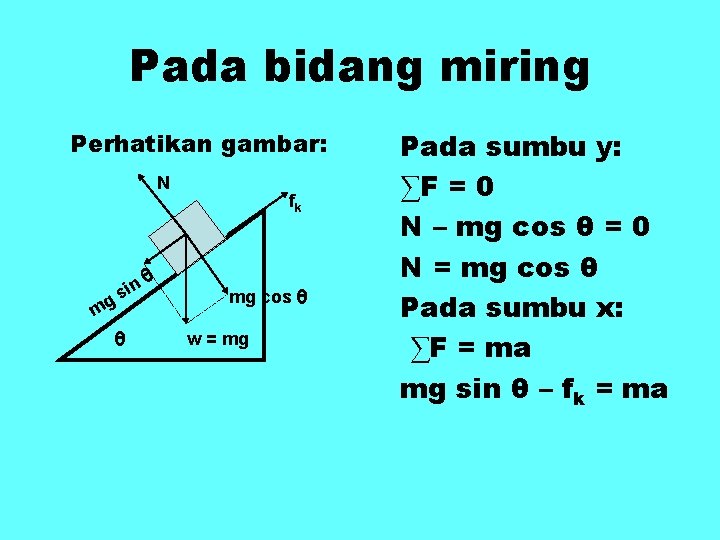
Pada bidang miring Perhatikan gambar: N mg sin θ θ fk mg cos θ w = mg Pada sumbu y: ∑F = 0 N – mg cos θ = 0 N = mg cos θ Pada sumbu x: ∑F = ma mg sin θ – fk = ma
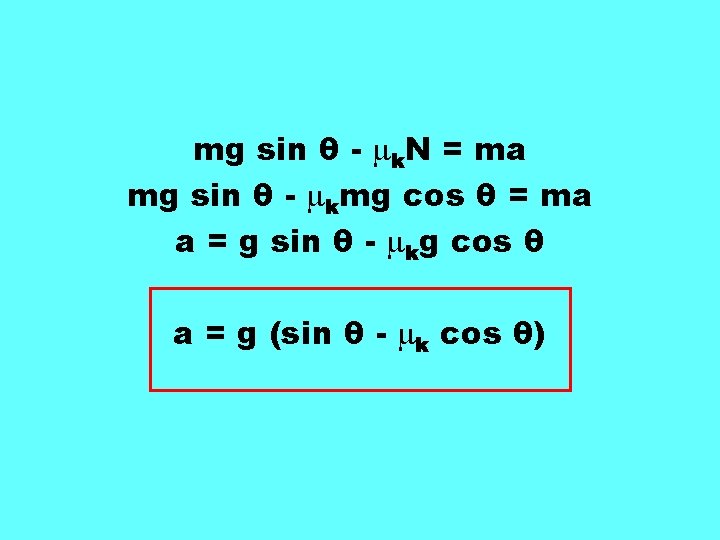
mg sin θ - k. N = ma mg sin θ - kmg cos θ = ma a = g sin θ - kg cos θ a = g (sin θ - k cos θ)
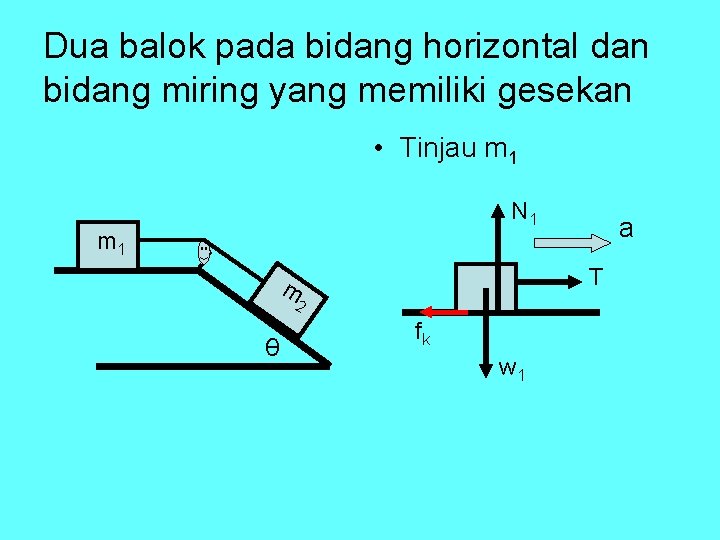
Dua balok pada bidang horizontal dan bidang miring yang memiliki gesekan • Tinjau m 1 N 1 m 1 T m 2 θ a fk w 1
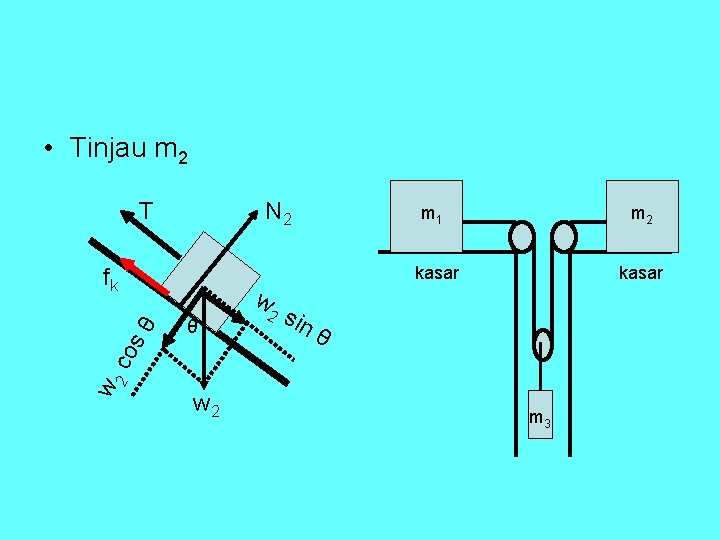
• Tinjau m 2 T N 2 fk θ 2 sin m 2 kasar θ w 2 co sθ w m 1 w 2 m 3
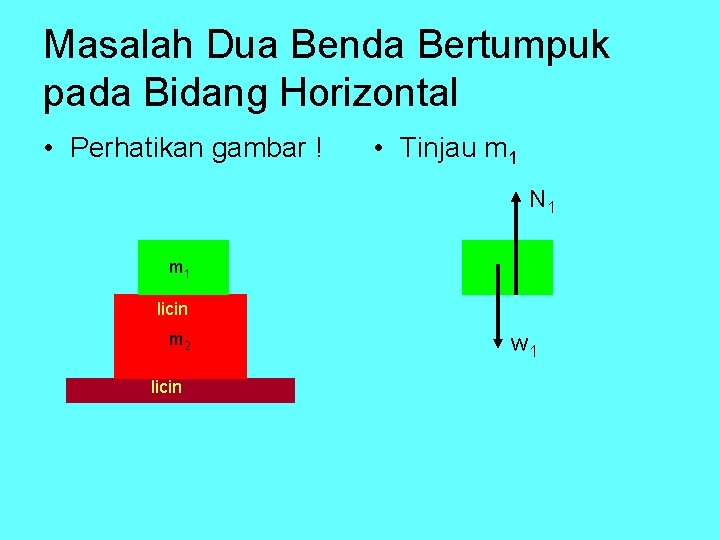
Masalah Dua Benda Bertumpuk pada Bidang Horizontal • Perhatikan gambar ! • Tinjau m 1 N 1 m 1 licin m 2 licin w 1
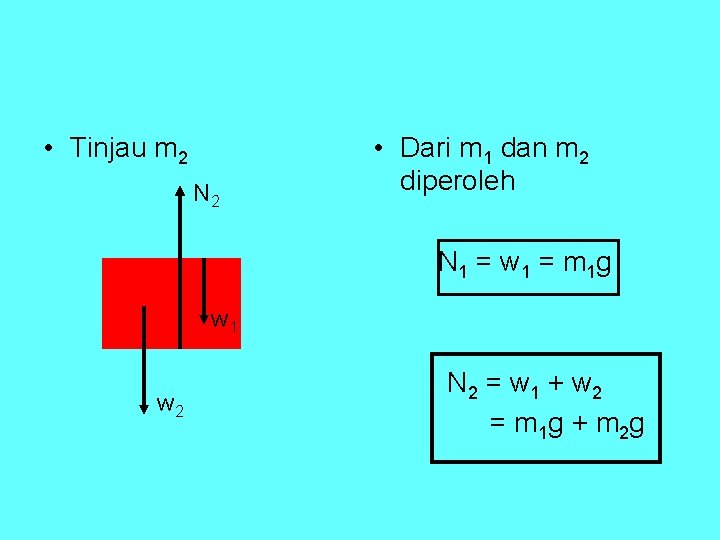
• Tinjau m 2 N 2 • Dari m 1 dan m 2 diperoleh N 1 = w 1 = m 1 g w 1 w 2 N 2 = w 1 + w 2 = m 1 g + m 2 g

Masalah dua balok bertumpukan di atas lantai horizontal

• Dari gambar di atas tentukan: a. percepatan maksimum yang diperbolehkan pada supir untuk menjalankan mobil agar kotak tidak meluncur terhadap mobil. b. percepatan kotak terhadap atap mobil jika mobil dijalankan melebihi percepatan maksimum.
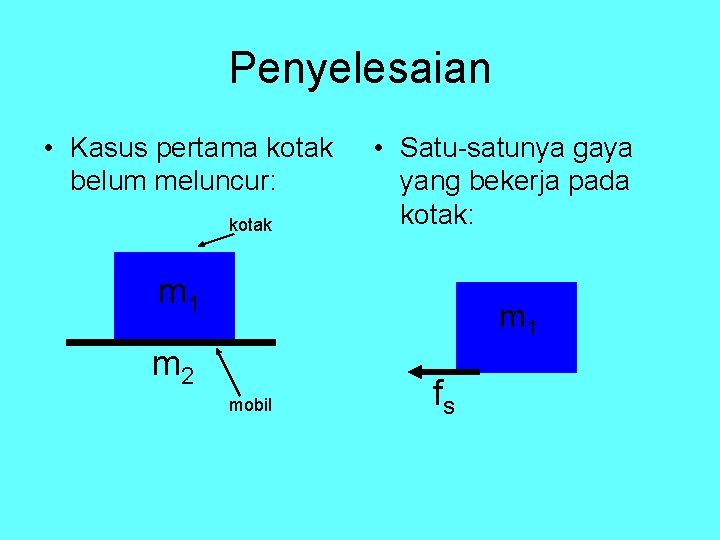
Penyelesaian • Kasus pertama kotak belum meluncur: kotak • Satu-satunya gaya yang bekerja pada kotak: m 1 m 2 mobil fs

• Kasus kedua kotak meluncur, maka fs berubah menjadi fk:

Aplikasi • Sebuah truk bak terbuka membawa sebuah peti (lihat gambar). Peti tidak diikat terhadap lantai tetapi koefisien s antara peti dan papan truk adalah 0, 7. Ketika lampu merah berganti hijau pada suatu jalan raya datar, supir mulai mempercepat truknya. Berapakah percepatan maksimum truk agar peti tidak meluncur ke belakang terhadap lantai truk? Jika peti berada 3 m jauhnya dari ujung bak terbuka, akankah peti itu jatuh dari truk dalam 2 sekon pertama dari geraknya ketika supir tepat melampui percepatan maksimum? Ambil koefisien gesekan kinetik k= 0, 6
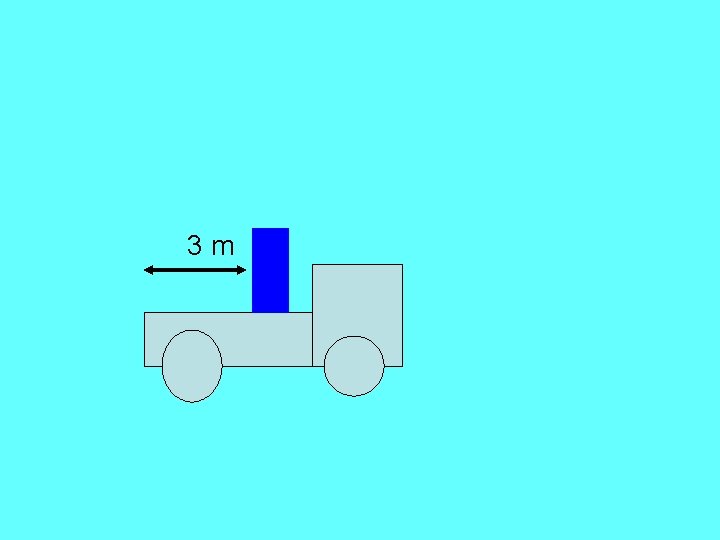
3 m

• Dari gambar diperoleh: Ø Sebuah mobil menempuh belokan pada jalan datar, yang memiliki jari-jari kelengkungan 25 m. koefesien gesekan statis antara ban dan jalan adalah 0, 4. Berapakah kelajuan maksimum mobil agar tidak slip?
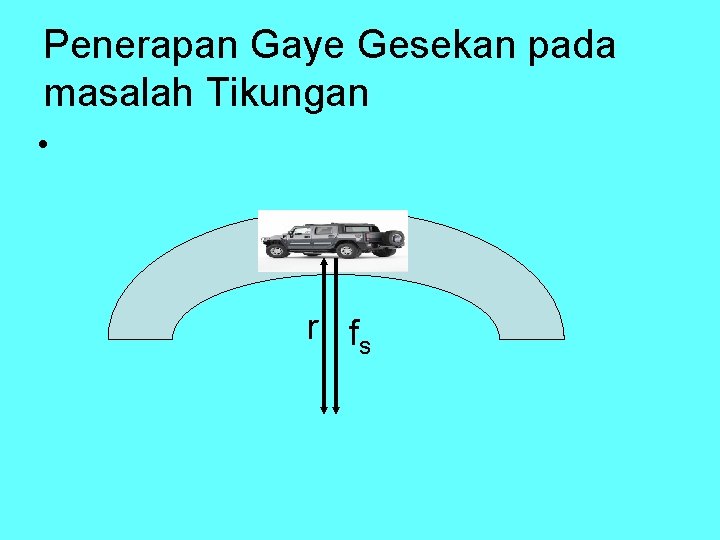
Penerapan Gaye Gesekan pada masalah Tikungan • r fs
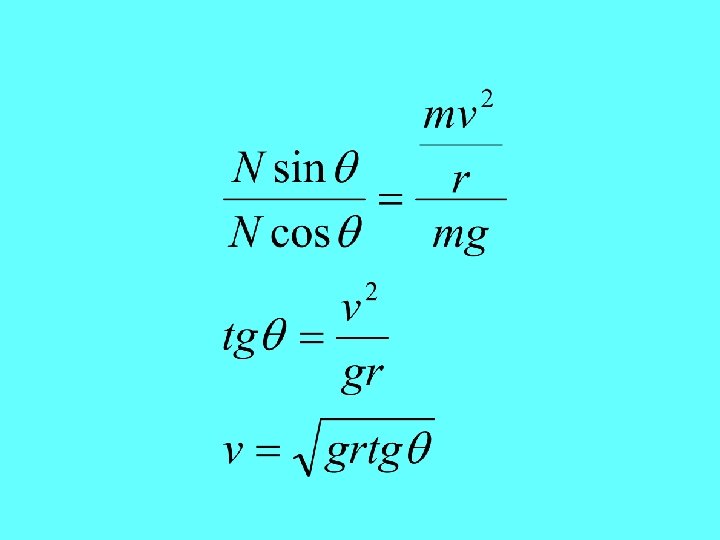
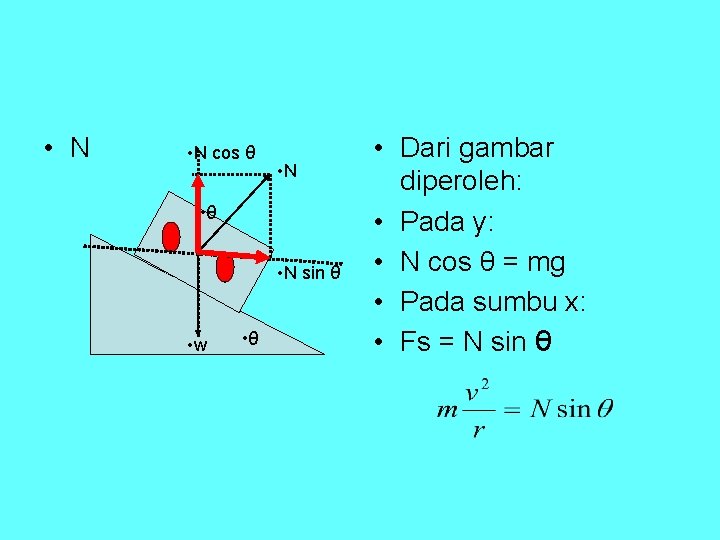
• N cos θ • N • θ • N sin θ • w • θ • Dari gambar diperoleh: • Pada y: • N cos θ = mg • Pada sumbu x: • Fs = N sin θ
- Slides: 43