Normalization Well structured relations and anomalies Normalization First

Normalization • • • Well structured relations and anomalies Normalization First normal form (1 NF) Functional dependence Partial functional dependency Second normal form (2 NF) Transitive functional dependency Third normal form (3 NF) Practical consideration

A well structured relation • Contains a minimum amount of redundancy • Allows users to modify, insert and delete the rows in a table without errors or inconsistencies EMPLOYEE 1 - Emploee 1 is a well structured relation. - Any modification to an employee’s data such as a change in salary, is confined to one row of the table.

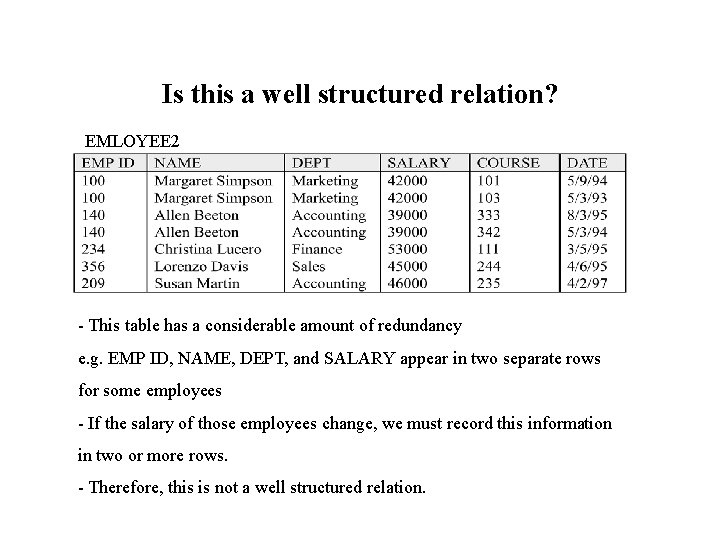
Is this a well structured relation? EMLOYEE 2 - This table has a considerable amount of redundancy e. g. EMP ID, NAME, DEPT, and SALARY appear in two separate rows for some employees - If the salary of those employees change, we must record this information in two or more rows. - Therefore, this is not a well structured relation.

Why minimize redundancies? • Redundancies in a table may result in errors and inconsistencies (called anomalies) when a use attempts to update the data in the table • Three types of anomalies – Insertion anomaly – Deletion anomaly – Modification anomaly

Insertion anomaly • If we want to add a new employee to EMPLOYEE 2, the user must supply values for EMPID and COURSE. • This is because the primary key values cannot be NULL. • In reality, employee should be able to enter employee data without supplying course data

Deletion anomaly • If the data for employee number 234 is deleted, we will also lose the information that this employee completed the course 111. • In fact, we lose information about the course altogether. Modification anomaly • Suppose that employee number 100 gets a salary increase, we must record this increase in each of the rows for that employee. • Otherwise the data will be inconsistent.

Normalization • Normalization is a process for converting complex data structures into simple, stable data structures (E. Codd 1970) • The objectives of the normalization process are: – to eliminate certain kinds of data redundancy, – to avoid certain anomalies. • Normalization is accomplished in stages. • A normal form is a state of a relation that can be determined by applying simple rules regarding dependencies (or relationships between attributes)

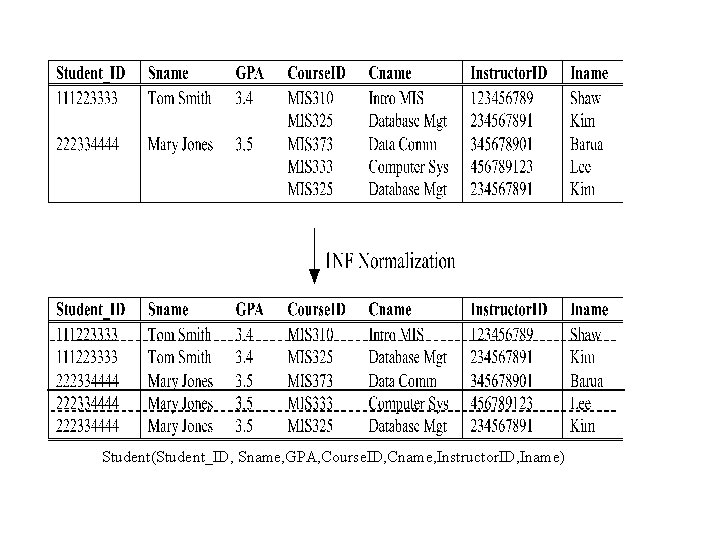
First Normal Form (1 NF) • Every attribute in each record contains only one value, i. e. a table contains NO REPEATING GROUPS! • A relation is already (at least) in 1 NF • A table with repeating groups is converted to a relation in first normal form by: extending the data in each column to fill the cells that are empty because of the repeating groups structures.

Student(Student_ID, Sname, GPA, Course. ID, Cname, Instructor. ID, Iname)

Functional dependence • A functional dependency is a particular relationship between two attributes • For any relation R, the attribute B is functionally dependent on A if for every instance of A, that value of A uniquely determines the value of B. • Represented as A -> B • Normalization is based on the analysis of functional dependence

Examples of functional dependency SSN -> NAME, ADDRESS, BIRTHDATE A person’s name, address and birthdate are functionally dependent on that person’s social security number. VIN -> MAKE, MODEL, COLOR The make, model and color of a vehicle are functionally dependent on the vehicle identification number ISBN -> TITLE The title of a book is functionally dependent on the book’s international standard book number (ISBN)

Determinant • The attribute on the left hand side of the arrow in a functional dependency is called a determinant. e. g. SSN, VIN, ISBN are determinants Important! • Instances (or sample data) in a relation do not prove that a functional dependency exists. • Only knowledge of the problem domain is a reliable method for identifying a functional dependency

EMPLOYEE 2 = (EMPID, NAME, DEPT, SALARY, COURSE, DATE COMPLETED) • Functional dependencies: EMPID -> NAME, DEPT, SALARY EMPID, COURSE -> DATE COMPLETED • Therefore the only candidate key (and hence primary key) is a combination of EMPID and COURSE

EMPLOYEE 2 (EMPID, NAME, DEPT, SALARY, COURSE, DATE COMPLETED) • A composite key is a primary key that contains more than one attribute. • EMPID is a determinant but not a candidate key. • A candidate key is always a determinant • But a determinant is not always a candidate key.

Partial functional dependency • A functional dependency A-> B is a partial dependency, if B is functionally dependent on A and also functionally dependent on any proper subset of A. • We check partial dependency if we have a composite key. EMPLOYEE 2= (EMPID, NAME, DEPT, SALARY, COURSE, DATE COMPLETED) The functional dependencies are: EMPID, COURSE -> DATE COMPLETED, EMPID -> NAME, DEPT, SALARY

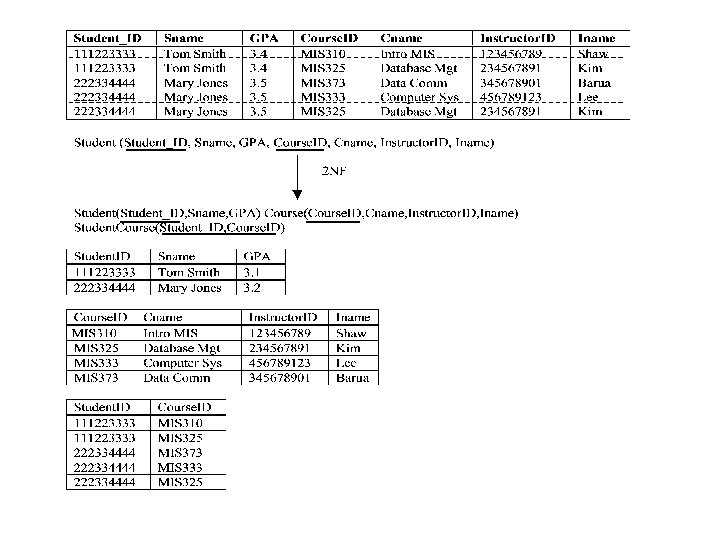
Second Normal Form (2 NF) • A relation is in second normal form if: - It is in first normal form, and - every nonkey attribute is functionally dependent on part (but not all) of the primary key, i. e. no partial functional dependency. • The conditions of 2 NF - The primary key consists of only one attribute, - No nonkey attributes exist, or - Every nonkey attribute is functionally dependent on the full set of primary key attributes.

Problems created by partial functional dependencies? • Insertion anomaly – To insert a row, we must provide values for both EMPID and COURSE • Deletion anomaly – If we delete a row for an employee, we lose the information that the employee completed a course on a particular date • Modification anomaly – If an employee’s salary changes, we must record this change in multiple rows (if the employee completed more than one course)

Removing partial dependencies If a relation is not in 2 NF, it can be further normalized into a number of 2 NF relations in which nonkey attributes are associated only with the part of the primary key on which they are fully functionally dependent. EMPLOYEE 2 = (EMPID, NAME, DEPT, SALARY, COURSE, DATE COMPLETED) EMPID, COURSE->Date. Completed and EMPID->Name, Dept, Salary EMPLOYEE (EMPID, NAME, DEPT, SALARY) EMPCOURSE (EMPID, COURSE, DATE COMPLETED)

Transitive dependency • A functional dependency between two (or more) nonkey attributes. • A set of attributes Y that is not a subset of the primary key of R, and both X->Y and Y->Z hold, i. e. X->Y and Y->Z, then X->Z. E. g. STUDENT NUMBER -> MAJOR and MAJOR -> ADVISOR then STUDENT NUMBER ->ADVISOR

Transitivity dependency Pseudotransitivity Rule: • If X->Y and YZ->W, then XZ->W e. g. STUDENT NUMBER->MAJOR and MAJOR, CLASS->ADVISOR, then STUDENT NUMBER, CLASS->ADVISOR

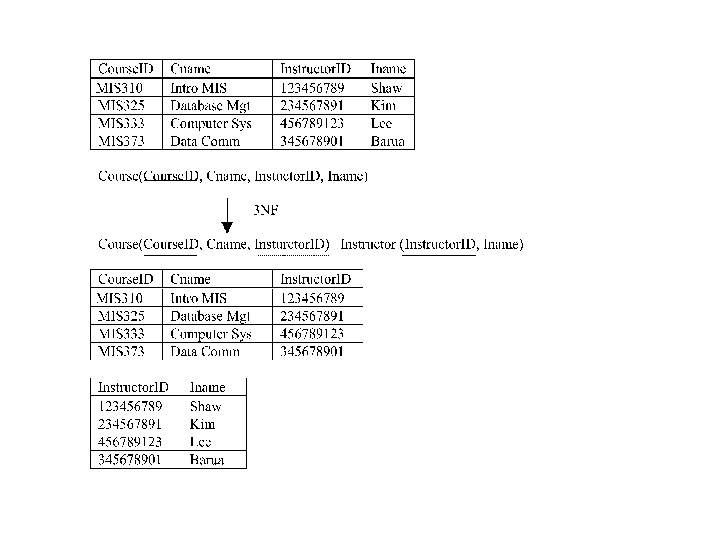
Third Normal Form (3 NF) • To eliminate the anomalies caused by the presence of transitive dependencies in a relation. • If a relation is in 3 NF, it is also in second normal form and no transitive dependencies exist. • 3 NF normalization: the nonkey attributes connected by each functional dependency which causes the transitive functional dependency become a new relation.

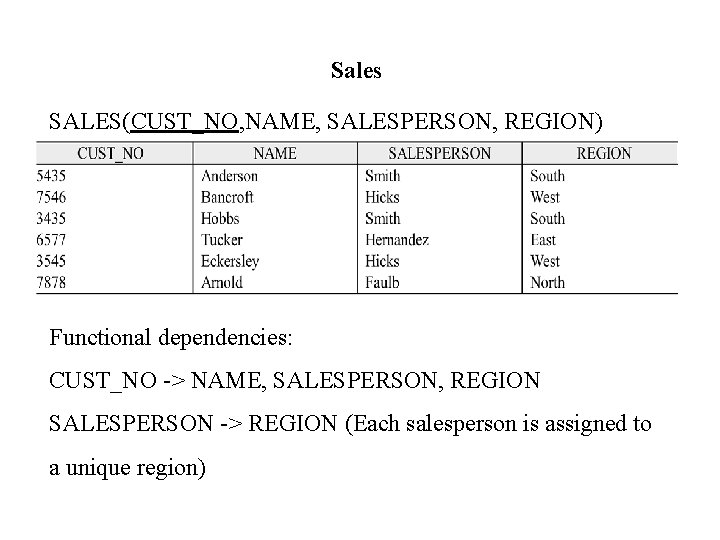
Sales SALES(CUST_NO, NAME, SALESPERSON, REGION) Functional dependencies: CUST_NO -> NAME, SALESPERSON, REGION SALESPERSON -> REGION (Each salesperson is assigned to a unique region)

Anomalies with Sales • Insertion Anomaly: A new salesperson Robinson assigned to the North region cannot be entered until a customer has been assigned. • Deletion Anomaly: If Customer Number 6577 is deleted from the relation, we lose the information that Hernandez is assigned to the East region • Modification anomaly: If salesperson Smith is reassigned to the East region, several rows must be changed to reflect that fact.

Removing transitive dependencies The transitive dependencies can be removed by: Decomposing SALES into two relations: SALES 1: (CUST NO, NAME, SALESPERSON) SPERSON (SALESPERSON, REGION) The determinant in the transitive dependency in SALES (i. e. SALESPERSON dependency) becomes primary key in the SPERSON & foreign key in the SALES 1 relation

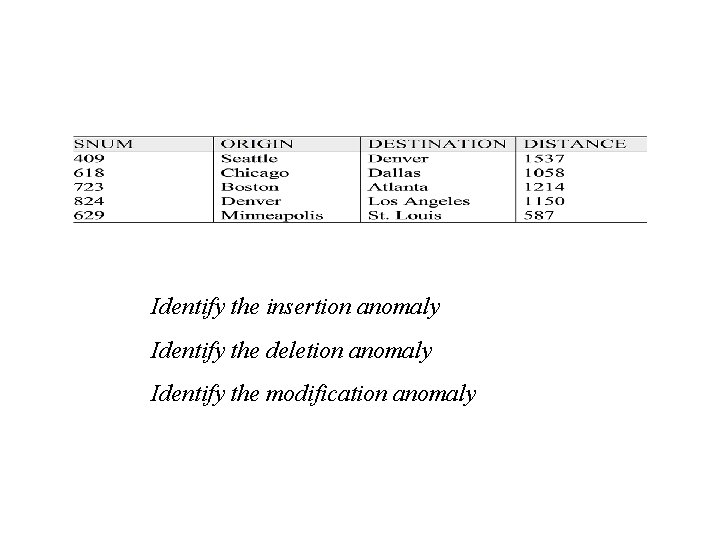
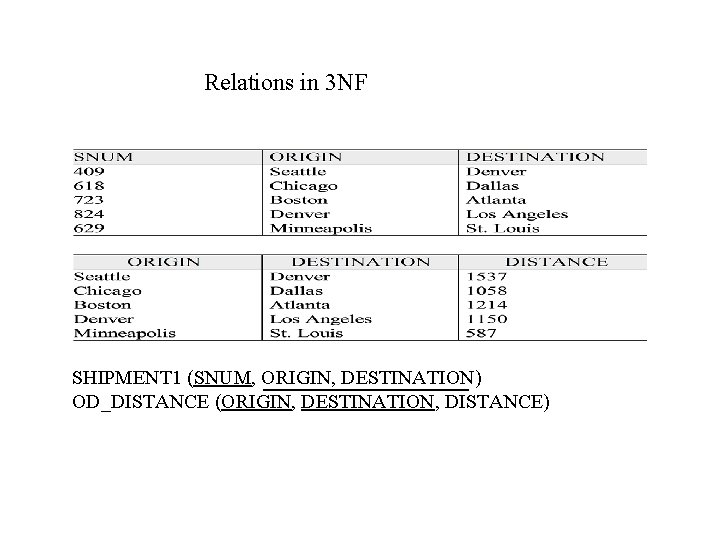
Transitive dependency between sets of attributes • Transitive dependency can occur between sets of attributes in a relation. E. g. SHIPMENT (SNUM, ORIGIN, DESTINATION, DISTANCE) Functional dependencies: SNUM -> ORIGIN, DESTINATION, DISTANCE ORIGIN, DESTINATION -> DISTANCE

Identify the insertion anomaly Identify the deletion anomaly Identify the modification anomaly

Relations in 3 NF SHIPMENT 1 (SNUM, ORIGIN, DESTINATION) OD_DISTANCE (ORIGIN, DESTINATION, DISTANCE)

ER Model and Third Normal Form (3 NF) • In general, if we have a “good” ER model and convert this model to relation schemes according to the transformation rules, we can get the relations with 3 NF.

Additional Normal Forms • Relations in third normal form are sufficient for most practical database applications • However, 3 NF does not guarantee that all anomalies have been removed. • There additional normal forms to remove them: Boyce-Codd Normal Form Fourth Normal Form Fifth Normal Form Domain Key Normal Form

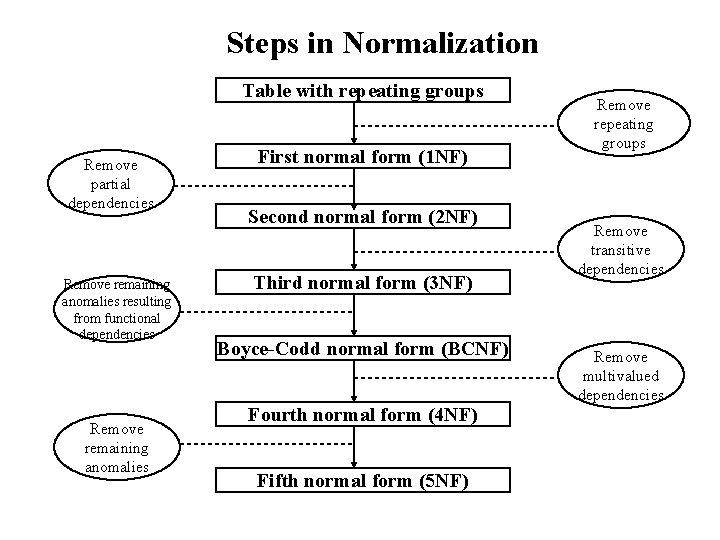
Steps in Normalization Table with repeating groups Remove partial dependencies Remove remaining anomalies resulting from functional dependencies Remove remaining anomalies First normal form (1 NF) Second normal form (2 NF) Third normal form (3 NF) Boyce-Codd normal form (BCNF) Fourth normal form (4 NF) Fifth normal form (5 NF) Remove repeating groups Remove transitive dependencies Remove multivalued dependencies