NORMALISATION Normal Forms 1 NF 2 NF 3

NORMALISATION Ø Normal Forms: Ø 1 NF Ø 2 NF Ø 3 NF Ø BCNF Ø 4 NF Ø 5 NF Ø DKNF (only theoretical)

1 NF teacher PAUL subject O. R • A relation. MATHS is said to be RAM in 1 nf if it OOPS has atomic values. NEURAL ANAND IMAGE TEACHER PAUL RAM ANAND SUBJECT O. R MATHS OOPS NEURAL IMAGE

MODIFICATION ANOMALIES • ACTIVITY (sid, activity, fee) • key: sid • INSERTION ANOMALIES • DELETION • ANOMALIES sid activity Fee 100 cricket 200 150 swimming 50 175 driving 50 200 swimming 50

FUNCTIONAL DEPENDENCIES • BLOCK-NAME RENT • Determinant Sid (Block, Room) ACTIVITY Fee X (Y, Z) X Y and X Z (X, Y) Z / X Z or Y Z

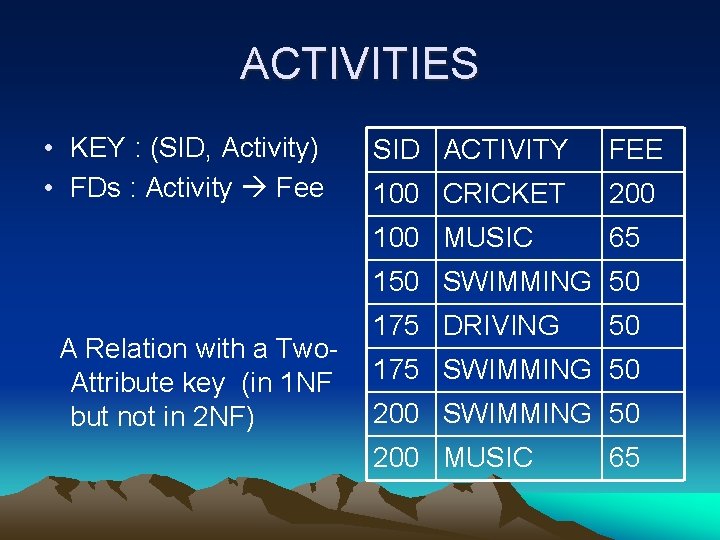
ACTIVITIES • KEY : (SID, Activity) • FDs : Activity Fee SID ACTIVITY FEE 100 CRICKET 200 100 MUSIC 65 150 SWIMMING 50 A Relation with a Two. Attribute key (in 1 NF but not in 2 NF) 175 DRIVING 50 175 SWIMMING 50 200 MUSIC 65

2 NF • 1 NF+ All non-key attributes are dependebnt on all of the key. Decomposition ACTIVITIES[SID, ACTIVITY] Act-Fee[Activity, Fee]

A RELATION WITH TRANSITIVE DEPENDENCY • Key : SID • FDs : Building Fee SID Building Fee 100 BLOCK 10 1200 150 BLOCK 5 1100 200 BLOCK 10 1200 250 BLOCK 4 1100 300 BLOCK 10 1200

ELIMINATION OF TRANSITIVE DEPENDENCY • Stu - hostel • key : SID Building 100 150 200 250 300 BLOCK 10 BLOCK 5 BLOCK 10 BLOCK 4 BLOCK 10 • Bldg-Fee Key : Building Block 10 Block 5 Block 4 Fee 1200 1100

Relation in 3 NF • ADVISOR • Key : ( primary ) : (SID, Major) • Key : (Candidate) : (SID, Fname) • Functional Dependencies : Fname Major SID Major Fname 100 150 200 250 300 MATHS CSE PAUL RAM RAJ PAUL ANAND

Relations in BCNF • Stu -Adv ($id, Fname) • Key : SID Fname 100 150 200 250 300 PAUL RAM RAJ PAUL ANAND • Adv-sub • Key : Fname • Fname Major PAUL MATHS RAM CSE RAJ MATHS ANAND CSE

Relation with multivalued dependencies STUDENT • KEY(sid, major, activity) • multivalued sid major dependencies sid activity sid major activity 100 100 150 maths Cs maths Swimming Tennies cricket

Insertion of a single tuple sid major activity 100 100 100 150 maths Cs maths foodball Swimming Tennies Cricket

Insertion of two tuples sid major activity 100 100 100 150 maths cs maths Cs Maths foodball Swimming Tennies Cricket

Elimination of MVDS • stu-major • key: sid, major sid 100 150 Major Maths Cs maths • stu-act • Key: sid, activiy sid 100 100 150 Activity football Swimming tennies cricket

Relation in 4 nf sid • STUDENT • KEY: sid 100 • FDS: sid shoe-size; 159 sid mariatal 200 -status 250 • MVDS: sid shoe-size/ mariatal-status • 4 nf if MVDS are implied by candidate keys of R Shoe-size 8 10 5 12 Martial-status M S S S

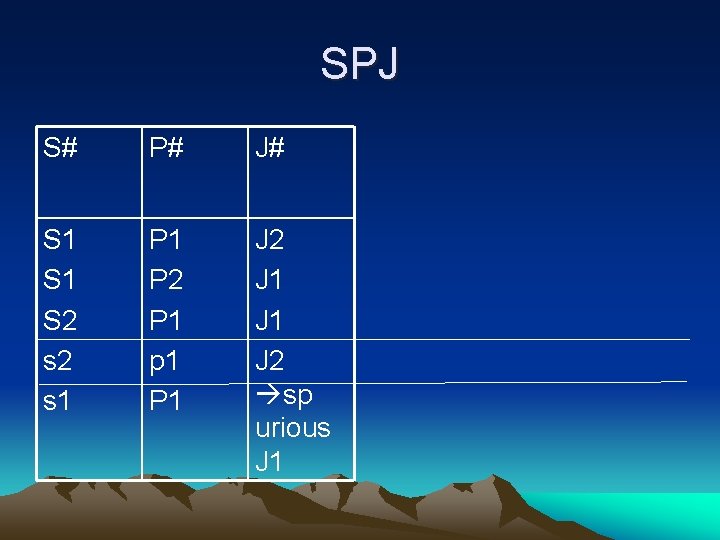
5 NF • Every JD in R is implid by candidate keys of R. SPJ: S# P# J# S 1 S 2 s 1 P 2 P 1 p 1 J 2 J 1 J 1

join over p# • SP: S# S 1 s 2 • PJ: P# P 1 P 2 P 1 p# P 1 P 2 P 1 join over p# J# j 2 j 1

SPJ S# P# J# S 1 S 2 s 1 P 2 P 1 p 1 P 1 J 2 J 1 J 2 sp urious J 1

J# j 2 j 1 s# S 1 S 2 • join over j#, s# original SPJ