Normal table and GDC Calculator needed Example Using

• Normal table and GDC (Calculator) needed!

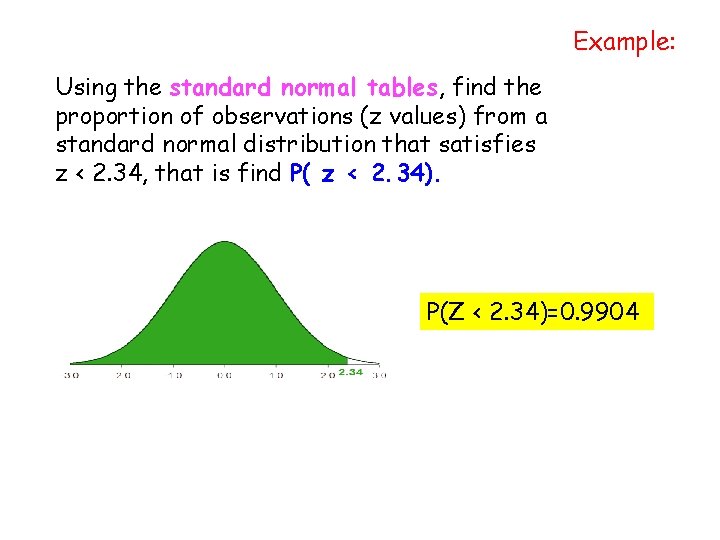
Example: Using the standard normal tables, find the proportion of observations (z values) from a standard normal distribution that satisfies z < 2. 34, that is find P( z < 2. 34). P(Z < 2. 34)=0. 9904

How to use GDC? 1. 2. 3. 4. Menu Probability (5) Distributions (5) Normal cdf (2)……… (lower bound, upper bound, Mean, Standard dev) • Never use Normalpdf! (It used for calculus purpose, like to find inflection point)

Example Use GDC to compute i) P( z < 2. 34) ii) P(z > 1. 67)

Inverse Normal Probability

Suppose we are interested in the finding the z* for the smallest 2%. To find z*: Look for the area. 0200 in the body of the Table. Follow the row and column back out to read the z-value. P(z < z*) =. 02 Since. 0200 doesn’t appear in the body of the z* = -2. 08 Table, use the value closest to it. z* -2. 1 -2. 0 -1. 9 . 0162. 0207. 0262 . 0158. 0202. 0256 … … . 08 … … . 07 … . 06 … … z* . 0154. 0197. 0250

Suppose we are interested in the finding the z* for the largest 5%. Since. 9500 is exactly between. 9495 and. 9505, . 95 we can average the z* for each of these P(z > z*) =. 05 z* = 1. 645 z* Remember the Table of Areas gives the area to the LEFT of z*. z* . 03 . 04 . 05 … 1. 5 1. 6 1. 7 . 9382. 9495. 9591 . 9398. 9505. 9599 … … … … 1 – (area to the right of z*) Then look up this value in the body of the table. . 9406. 9515. 9608

How to use GDC to find Invers Norm? 1. 2. 3. 4. Menu Probability (5) Distributions (5) Inverse Normal (3)……… (Area, Mean, Standard dev) * Area is area to the left of z*

Answer me! Using the standard normal tables, in each of the following, find the z values that satisfy : (a) The point z with 98% of the observations falling below it. Answer: The closest entry in the table to 0. 9800 is 0. 9798 corresponding to a z value of 2. 05

(b) The point z with 90% of the observations falling above it. Answer: The closest entry in the table to 0. 1000 is 0. 1003 corresponding to a z value of -1. 28

Standardizing NPD

The Standard Normal Probability Distribution … is a normal distribution with a mean of 0 and a standard deviation of 1. Also called the Z Distribution A z-value is the distance between a selected value (designated X) and the population mean, divided by the population A Standard Deviation, . z-value is, therefore, a location on the standard normal curve. Formula z µ ) (X = s

Finding Probabilities for Other Normal Curves • To find the probabilities for other normal curves, standardize the relevant values and then use the table of z areas. • If x is a random variable whose behavior is described by a normal distribution with mean m and standard deviation s , then P(x < b) = P(z < b*) P(x > a) = P(z > a*) Where z is a variable whose distribution is standard normal and

Example-1: Data on the length of time to complete registration for classes using an on-line registration system suggest that the distribution of the variable x = time to register for students at a particular university can well be approximated by a normal distribution with mean m = 12 minutes and standard deviation s = 2 minutes.

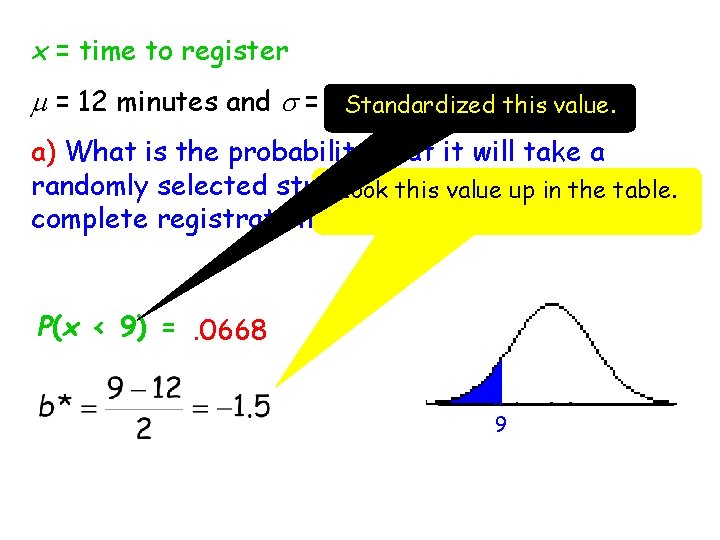
x = time to register m = 12 minutes and s = 2 Standardized minutes this value. a) What is the probability that it will take a randomly selected student 9 minutes to Lookless this than value up in the table. complete registration? P(x < 9) =. 0668 9

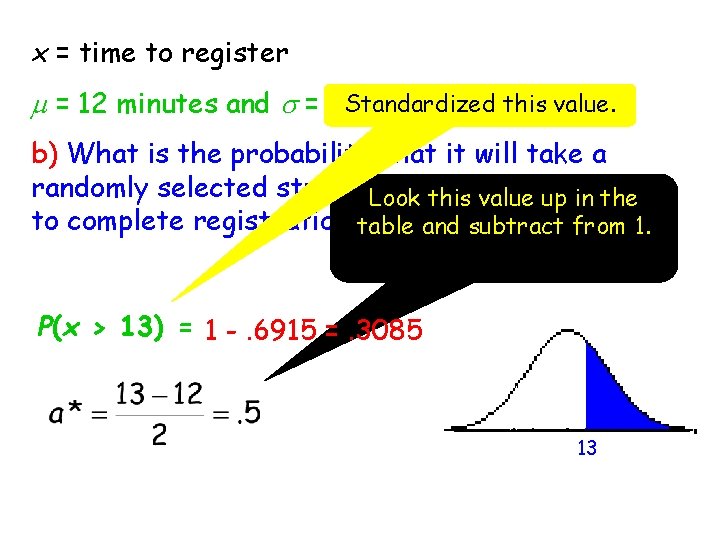
x = time to register this value. m = 12 minutes and s = 2 Standardized minutes b) What is the probability that it will take a randomly selected student. Look more thisthan value 13 upminutes in the to complete registration? table and subtract from 1. P(x > 13) = 1 -. 6915 =. 3085 13

x = time to register m = 12 minutes and s = 2 minutes c) What is the probability that it will take a randomly selected student between 7 and 15 minutes to complete registration? P(7 < x < 15) =. 9332 -. 0062 =. 9270 7 15

Use GDC to solve the following: What is the probability that it will take a randomly selected student between 7 and 15 minutes to complete registration? x = time to register m = 12 minutes and s = 2 minutes 7 15

Example-2 A Company produces “ 20 ounce” jars of a picante sauce. The true amounts of sauce in the jars of this brand sauce follow a normal distribution. Suppose the companies “ 20 ounce” jars follow a N(20. 2, 0. 125) distribution curve. (i. e. , The contents of the jars are normally distributed with a true mean = 20. 2 ounces with a true standard deviation = 0. 125 ounces. a) What proportion of the jars are under-filled? b) What proportion of the sauce jars contain between 20 and 20. 3 ounces of sauce? c) 99% of the jars of this brand of picante sauce will contain more than what amount of sauce?

Mr. Meyers has determined that the scores in his Calculus BC course are approximately normally distributed with a mean of 72 and a standard deviation of 5. He announces to the class that the top 15% of the scores will earn an A. What is the lowest score a student can earn and still receive an A?

Pair-work