Normal mode analysis NMA tutorial and lecture notes

Normal mode analysis (NMA) tutorial and lecture notes by K. Hinsen Serkan Apaydın

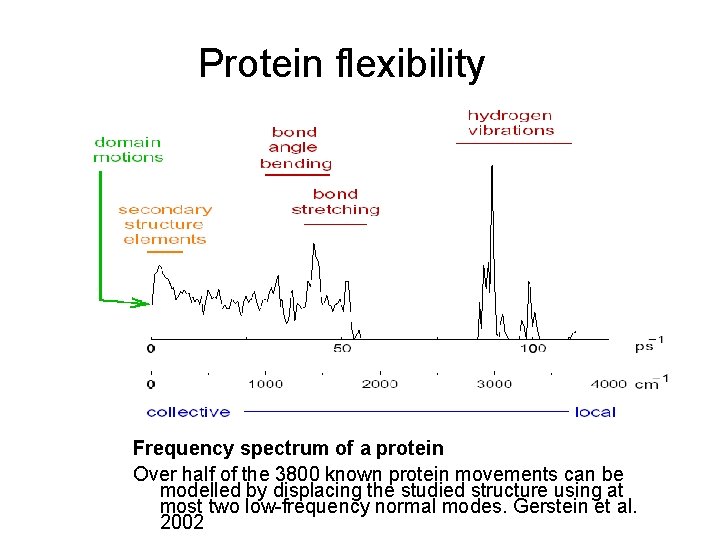
Protein flexibility Frequency spectrum of a protein Over half of the 3800 known protein movements can be modelled by displacing the studied structure using at most two low-frequency normal modes. Gerstein et al. 2002

Outline • NMA – What it is – Vibrational dynamics – Brownian modes – Coarse grained models – Essential dynamics

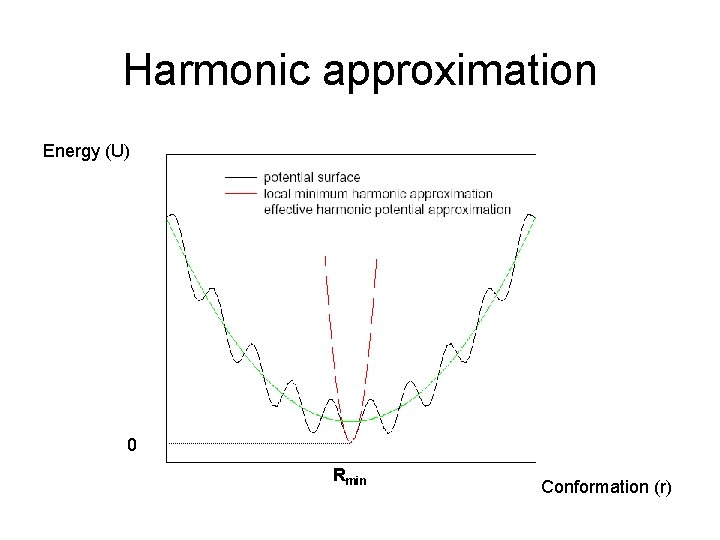
Harmonic approximation Energy (U) 0 Rmin Conformation (r)

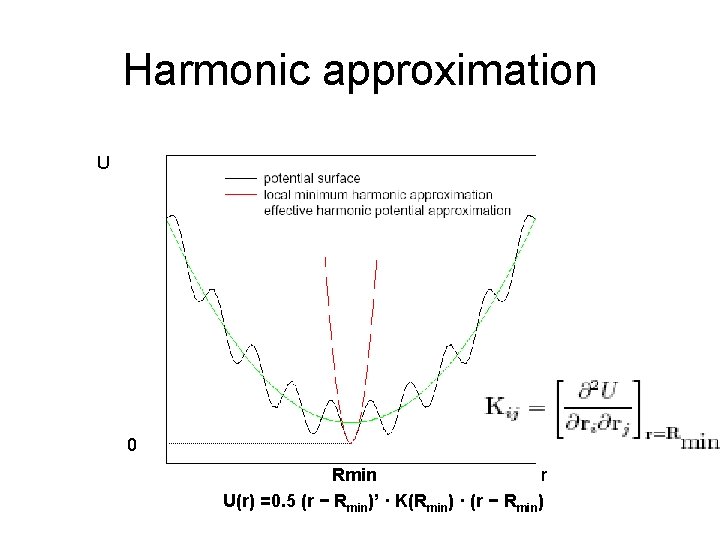
Harmonic approximation U 0 Rmin r U(r) =0. 5 (r − Rmin)’ · K(Rmin) · (r − Rmin)

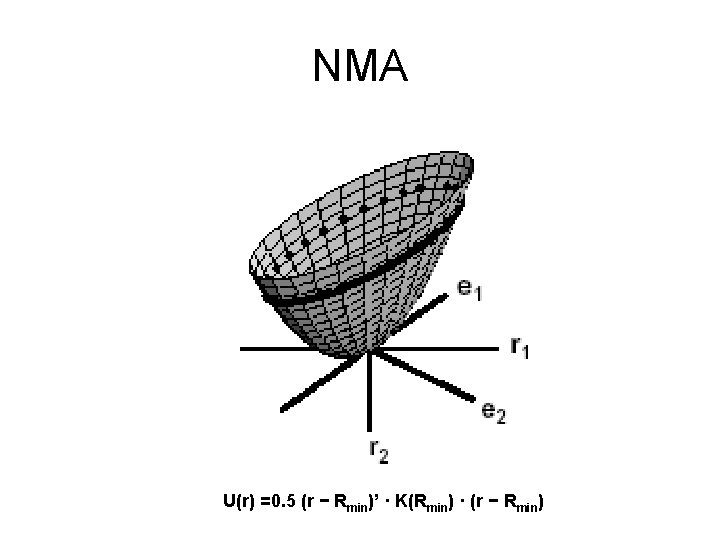
NMA U(r) =0. 5 (r − Rmin)’ · K(Rmin) · (r − Rmin)

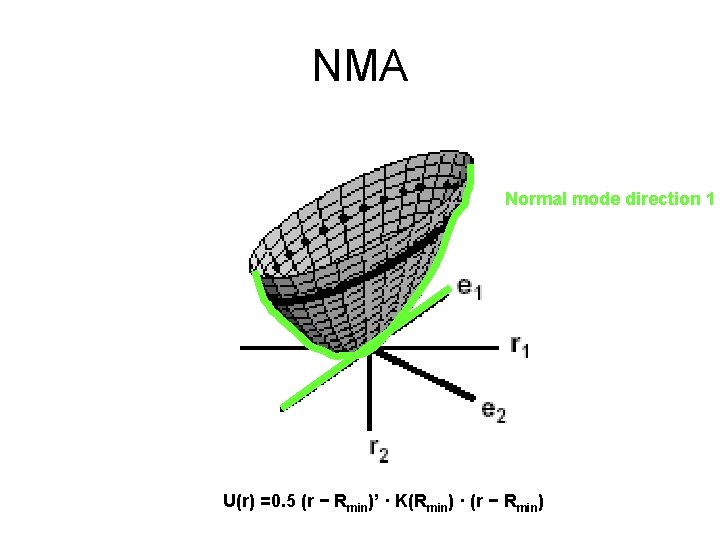
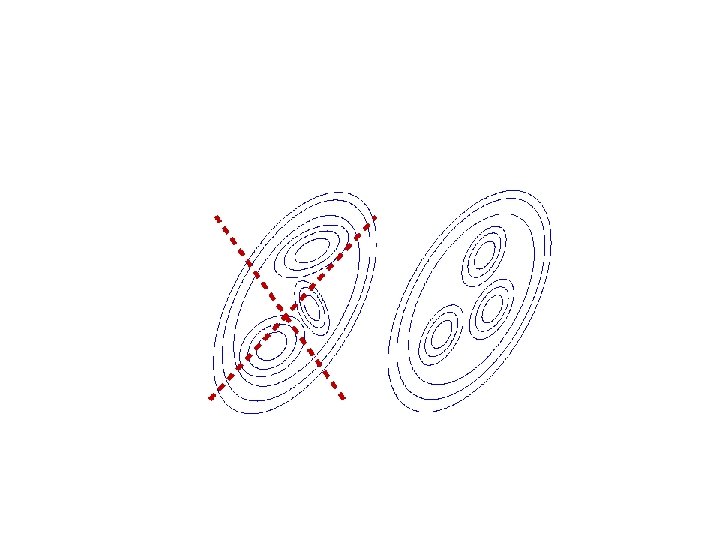
NMA Normal mode direction 1 U(r) =0. 5 (r − Rmin)’ · K(Rmin) · (r − Rmin)

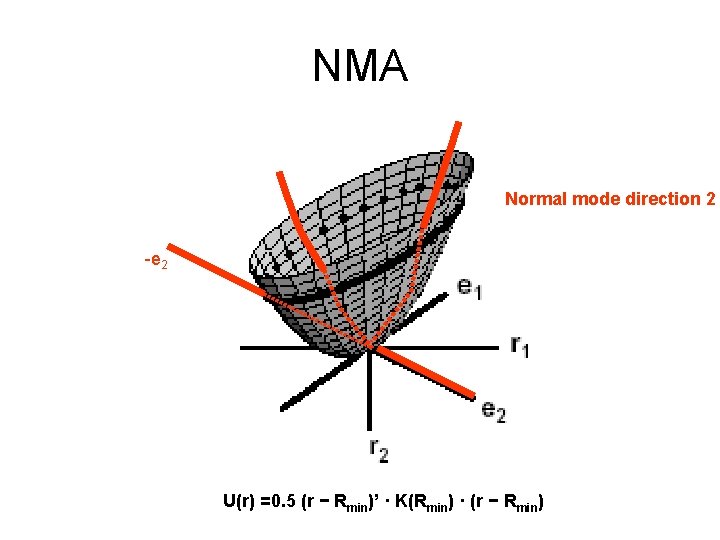
NMA Normal mode direction 2 -e 2 U(r) =0. 5 (r − Rmin)’ · K(Rmin) · (r − Rmin)

NMA (2) U(r) =0. 5 (r − Rmin)’ · K(Rmin) · (r − Rmin) min O(n 3)

Properties of NMA • The eigenvalues describe the energetic cost of displacing the system by one length unit along the eigenvectors. • For a given amount of energy, the molecule can move more along the low frequency normal modes • The first six eigenvalues are 0, corresponding to rigid body movements of the protein

4 ways of doing NMA A. Using minimization to obtain starting conformation, and computing the Hessian K: 1. 2. Vibrational NMA Brownian NMA B. Given starting structure: 1. Coarse grained models C. Given set of conformations corresponding to the motion of the molecule: 1. Essential Dynamics

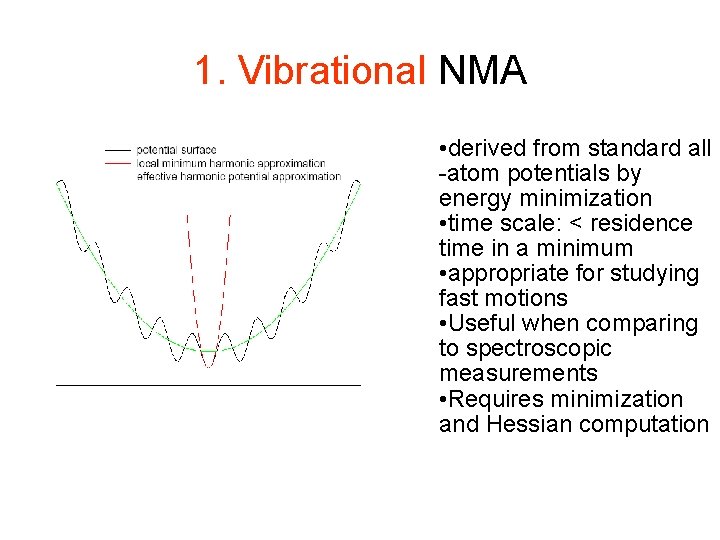
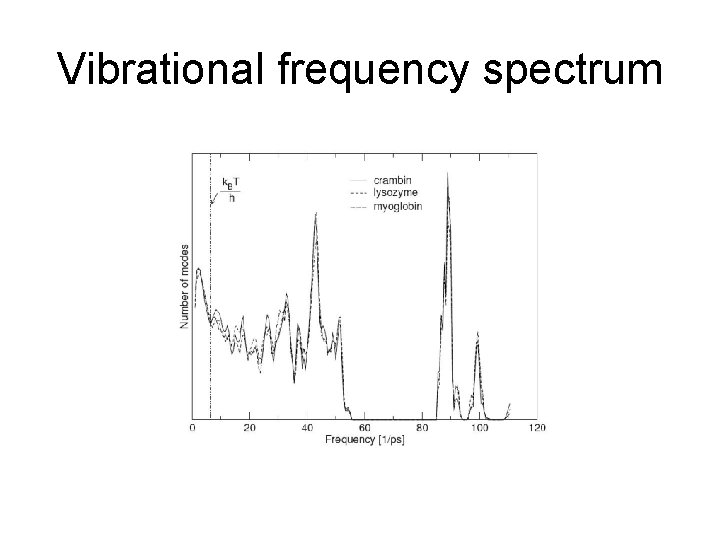
1. Vibrational NMA • derived from standard all -atom potentials by energy minimization • time scale: < residence time in a minimum • appropriate for studying fast motions • Useful when comparing to spectroscopic measurements • Requires minimization and Hessian computation

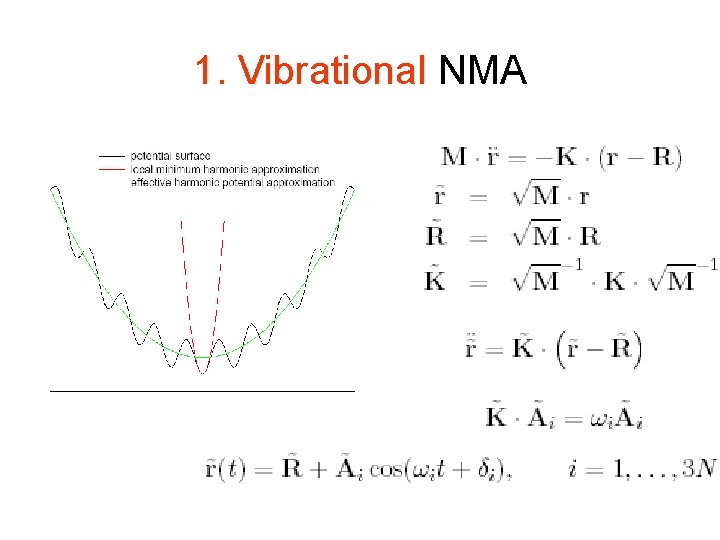
1. Vibrational NMA

Vibrational frequency spectrum

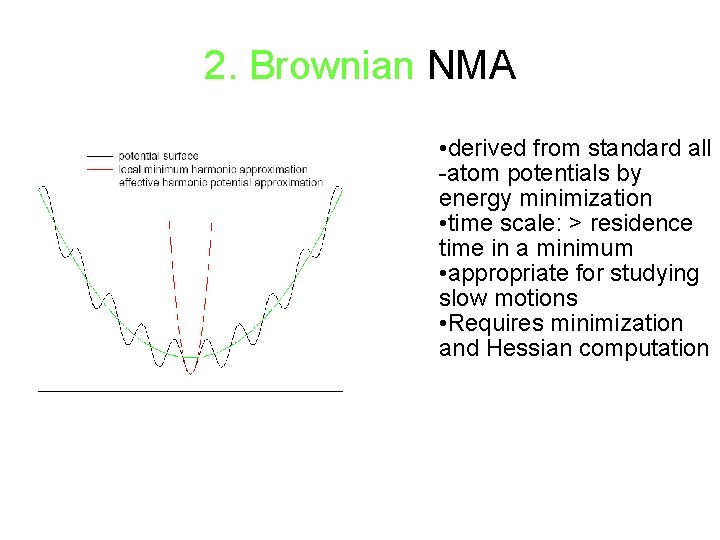
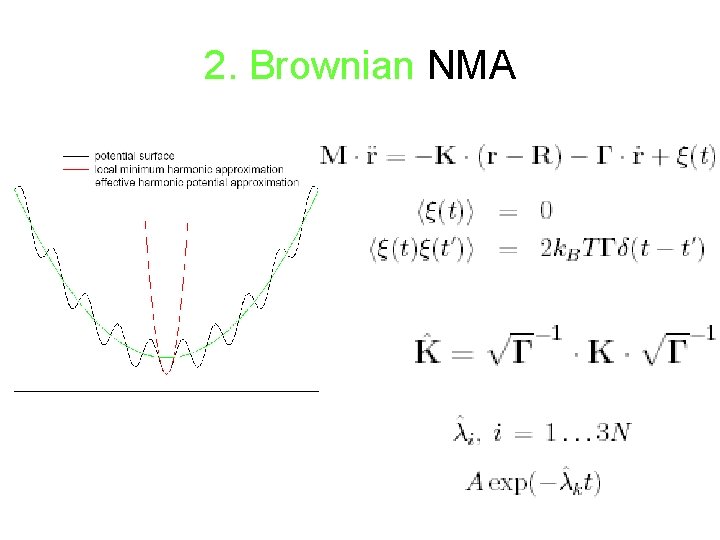
2. Brownian NMA • derived from standard all -atom potentials by energy minimization • time scale: > residence time in a minimum • appropriate for studying slow motions • Requires minimization and Hessian computation

2. Brownian NMA

The friction coefficients • describe energy barriers between conformational substates • Can be obtained from MD trajectories (<xi 2>) • Depend on local atomic density (not a solvent effect) http: //dirac. cnrs-orleans. fr/plone/Members/hinsen/

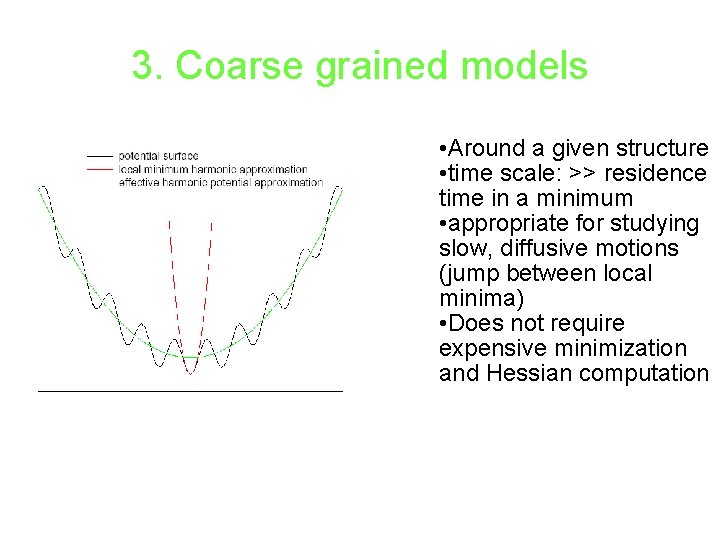
3. Coarse grained models • Around a given structure • time scale: >> residence time in a minimum • appropriate for studying slow, diffusive motions (jump between local minima) • Does not require expensive minimization and Hessian computation

3. Coarse grained models (2) • Capture collective motions – Specific to a protein – Usually related to its function – Largest amplitudes • Atoms are point masses • Springs between nearby points

Coarse grained models (3) f can be a step function or may have an exponential dependence. Elastic network model NMA (aka ANM) Find Hessian of V, then eigendecomposition Gaussian network model

Coarse grained models (4) All atom or C-alpha based models… • Or a step function…

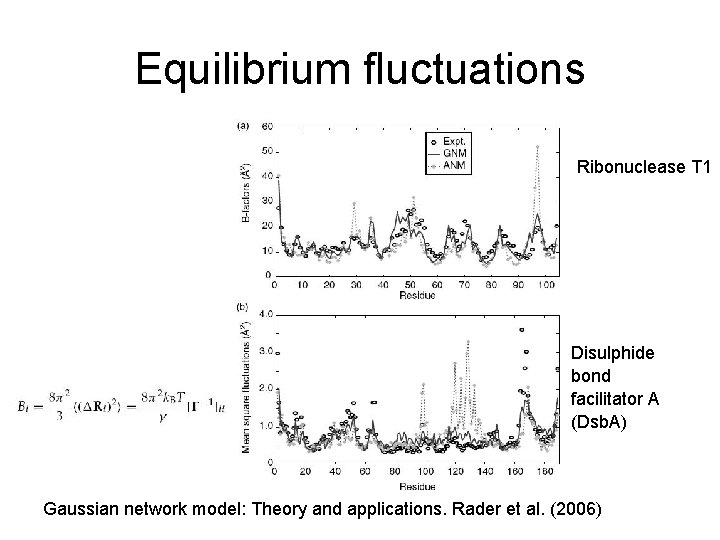
Equilibrium fluctuations Ribonuclease T 1 Disulphide bond facilitator A (Dsb. A) Gaussian network model: Theory and applications. Rader et al. (2006)

Difference between ENM NMA and GNM • GNM more accurate in prediction of meansquare displacements • GNM does not provide the normal mode directions

Lower resolution models • Groups of residues clustered into : • unified sites G Li, Q Cui - Biophysical Journal, 2002 • Rigid blocks (rotation and translation of blocks (RTB) model) • To examine larger biomolecular assemblies

4. Essential dynamics • Given a set of structures that reflect the flexibility of the molecule • Find the coordinates that contribute significantly to the fluctuations • time scale: >> residence time in a minimum

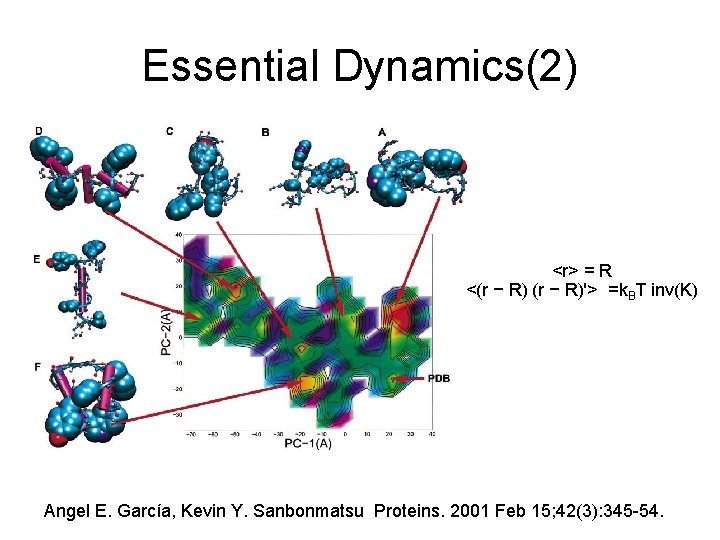
Essential Dynamics(2) <r> = R <(r − R)'> =k. BT inv(K) Angel E. García, Kevin Y. Sanbonmatsu Proteins. 2001 Feb 15; 42(3): 345 -54.

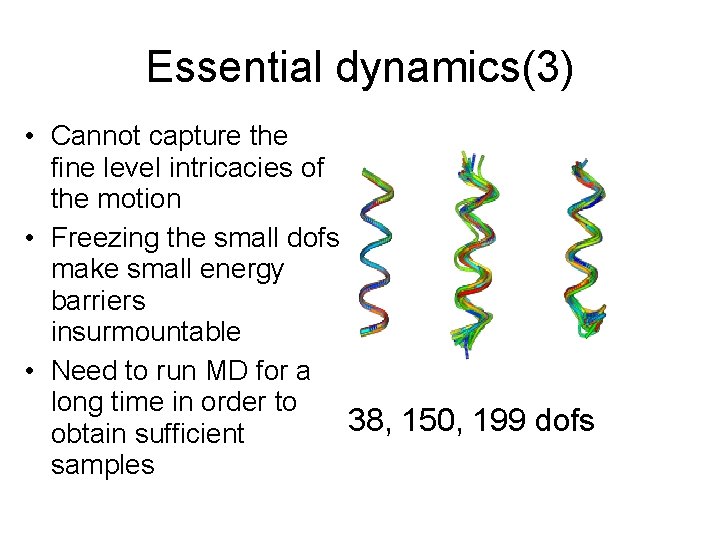
Essential dynamics(3) • Cannot capture the fine level intricacies of the motion • Freezing the small dofs make small energy barriers insurmountable • Need to run MD for a long time in order to 38, 150, 199 dofs obtain sufficient samples

Applications of normal modes • Use all modes or a large subset – Analytical representation of a potential well – Limitations: • approximate nature of the harmonic approximation • Choice of a subset • Properties of individual modes – Must avoid overinterpretation of the data • E. g. , discussing differences of modes equal in energy • No more meaningful than discussing differences between motion in an arbitrarily chosen Cartesian coord. system

Applications of normal modes (2) • Explaining which modes/frequencies are involved in a particular domain’s motion • Answered using projection methods: – Normal modes form a basis of the config. space of the protein – Given displacement d, pi = d · ei • Contribution of mode i to the motion under consideration – Cumulative contribution of modes to displacement

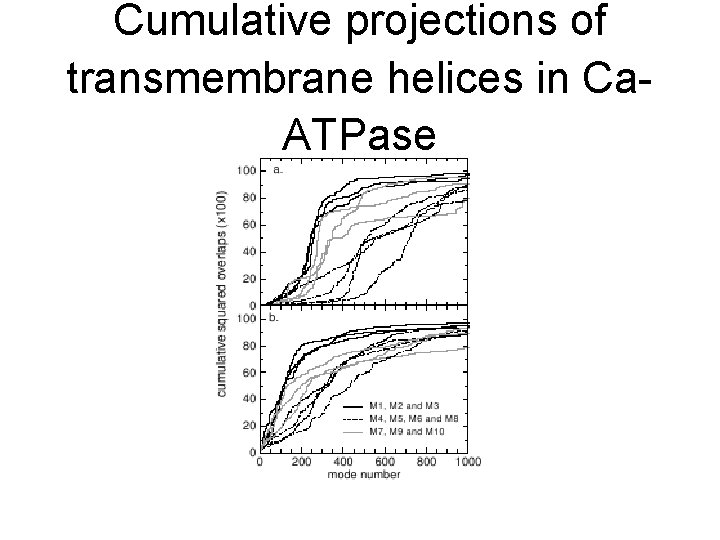
Cumulative projections of transmembrane helices in Ca. ATPase

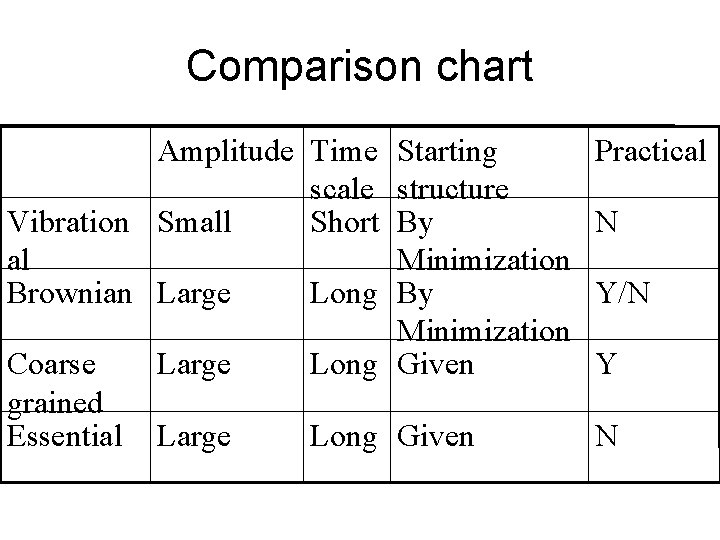
Comparison chart Amplitude Time Starting scale structure Vibration Small Short By al Minimization Brownian Large Long By Minimization Coarse Large Long Given grained Essential Large Long Given Practical N Y/N Y N

Summary NMA: • no sampling problem • computational efficiency, especially for coarse-grained models • simplicity in application • Predicts experimental quantities related to flexibility, such as B-factors, well.

• http: //igs-server. cnrs-mrs. fr/elnemo/ (all atom)

Web. NM: (C-alpha based) http: //www. bioinfo. no/tools/normalmodes

http: //promode. socs. waseda. ac. jp/pages/jsp/index. jsp (all-atom)

Ignm (C-alpha based): http: //ignm. ccbb. pitt. edu/

http: //molmovdb. org/nma/ (C-alpha based)

http: //lorentz. immstr. pasteur. fr/nomad-ref. php (all atomic or just C-alpha)

Protein Flexibility Predictions Using Graph Theory Jacobs, Rader, Kuhn and Thorpe Proteins: Structure, function and genetics 44: 150 -165 (2001) Serkan Apaydın

Characterizing intrinsic flexibility and rigidity within a protein 1. Compares different conformational states Limited by the diversity of the conformational states

Characterizing intrinsic flexibility and rigidity within a protein 2. Simulates molecular motion using MD Limited by the computational time

Characterizing intrinsic flexibility and rigidity within a protein 3. Identifies rigid protein domains or flexible hinge joints based on a single conformation Can provide a starting point for more efficient MD or MCS

Outline • • The main idea: constraint counting Brute force algorithm Rigidity theory Pebble game analysis Rigid cluster decomposition Flexibility Index Examples

Overview of FIRST • Floppy Inclusion and Rigid Substructure Topography • Given constraints: – Covalent bonds – hydrogen bonds – Salt bridges • Evaluate mechanical properties of the protein: Find regions that are: – rigid – move collectively – move independently of other regions Compute a relative degree of flexibility for each region

Rigidity in Networks – a history • • introduces constraints on the motions of mechanical systems 1864: Maxwell determined whether structures are stable or deformable 1788: Lagrange applications in engineering, such as the stability of truss configurations in bridges • 1970: Laman’s theorem: determines the degrees of freedom within 2 D networks and allow rigid and flexible regions to be found extended to bond-bending networks in 3 D http: //unabridged. m-w. com

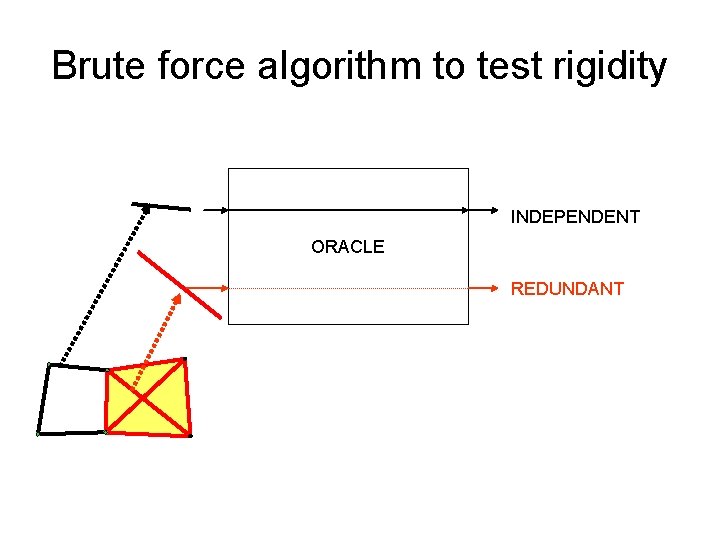
Brute force algorithm to test rigidity INDEPENDENT ORACLE REDUNDANT

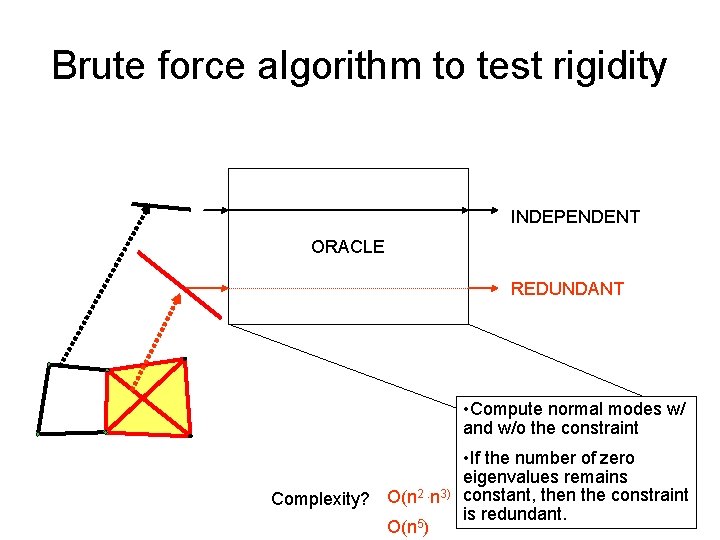
Brute force algorithm to test rigidity INDEPENDENT ORACLE REDUNDANT • Compute normal modes w/ and w/o the constraint Complexity? O(n 2. n 3) O(n 5) • If the number of zero eigenvalues remains constant, then the constraint is redundant.

Laman’s theorem accelerates constraint counting • Constraint counting to all the subgraphs – Applying directly, complexity is O(exp(n)) – Applying recursively, pebble game algorithm. Complexity is O(n 2), O(n) in practice.

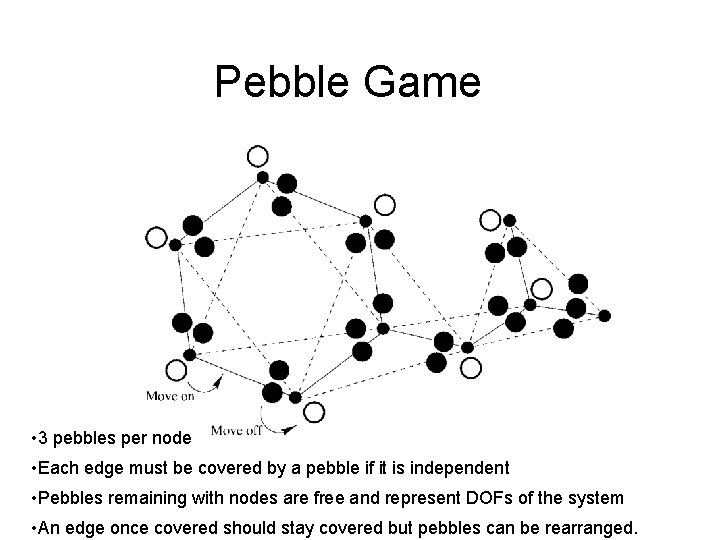
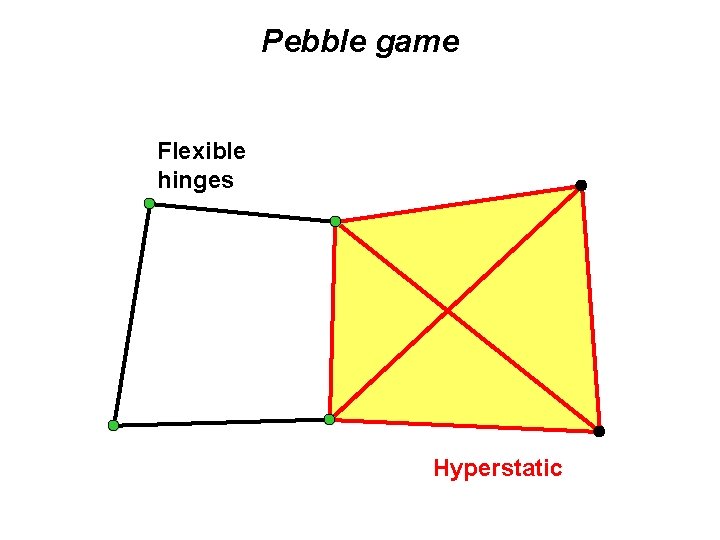
Pebble Game • 3 pebbles per node • Each edge must be covered by a pebble if it is independent • Pebbles remaining with nodes are free and represent DOFs of the system • An edge once covered should stay covered but pebbles can be rearranged.

The Pebble Game: A Demonstration Mykyta Chubynsky and M. F. Thorpe Arizona State University

Pebble game Flexible hinges Hyperstatic

Pebble game

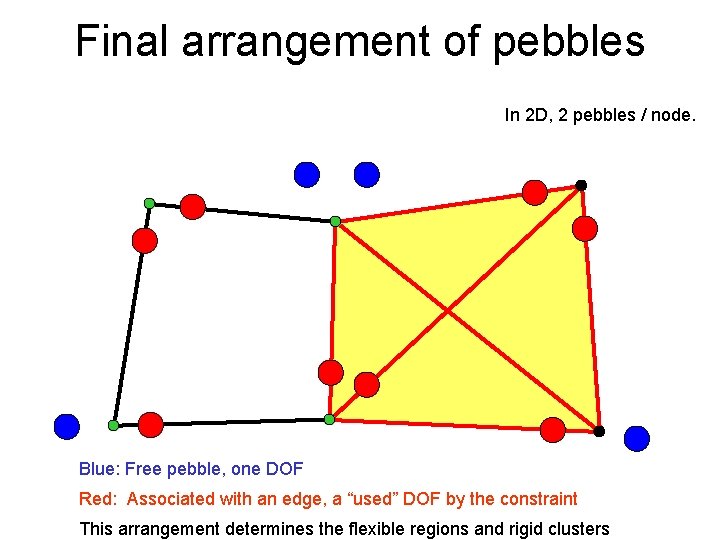
Final arrangement of pebbles In 2 D, 2 pebbles / node. Blue: Free pebble, one DOF Red: Associated with an edge, a “used” DOF by the constraint This arrangement determines the flexible regions and rigid clusters

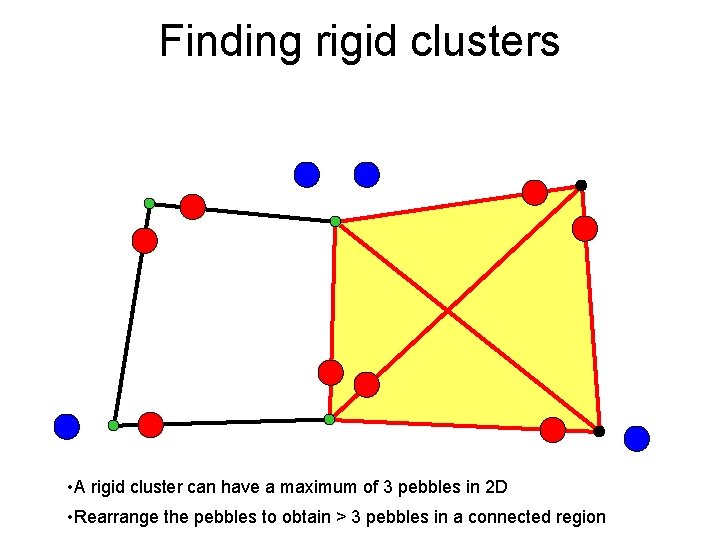
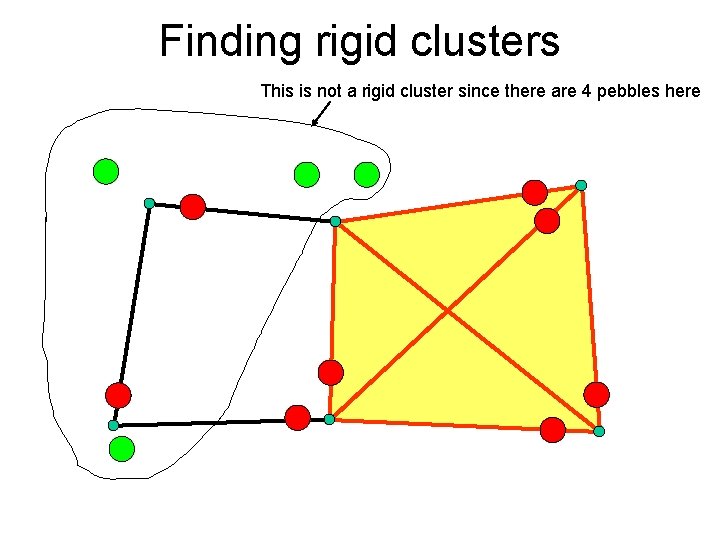
Finding rigid clusters • A rigid cluster can have a maximum of 3 pebbles in 2 D • Rearrange the pebbles to obtain > 3 pebbles in a connected region

Finding rigid clusters This is not a rigid cluster since there are 4 pebbles here

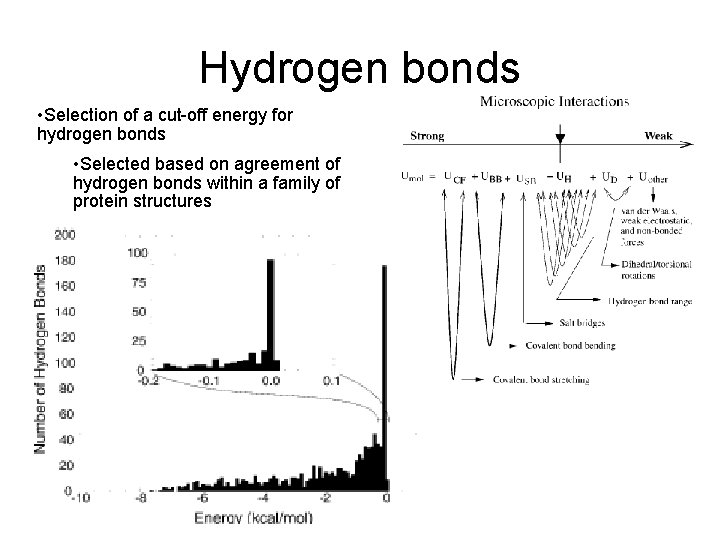
Hydrogen bonds • Selection of a cut-off energy for hydrogen bonds • Selected based on agreement of hydrogen bonds within a family of protein structures

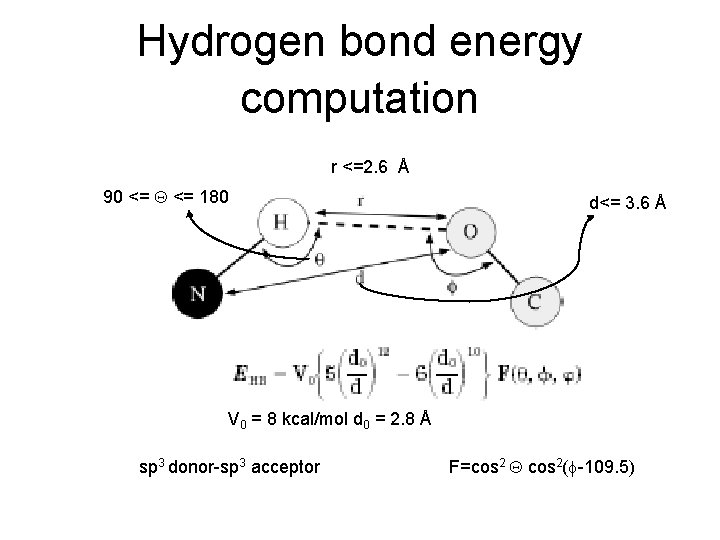
Hydrogen bond energy computation r <=2. 6 Å 90 <= 180 d<= 3. 6 Å V 0 = 8 kcal/mol d 0 = 2. 8 Å sp 3 donor-sp 3 acceptor F=cos 2 cos 2( -109. 5)

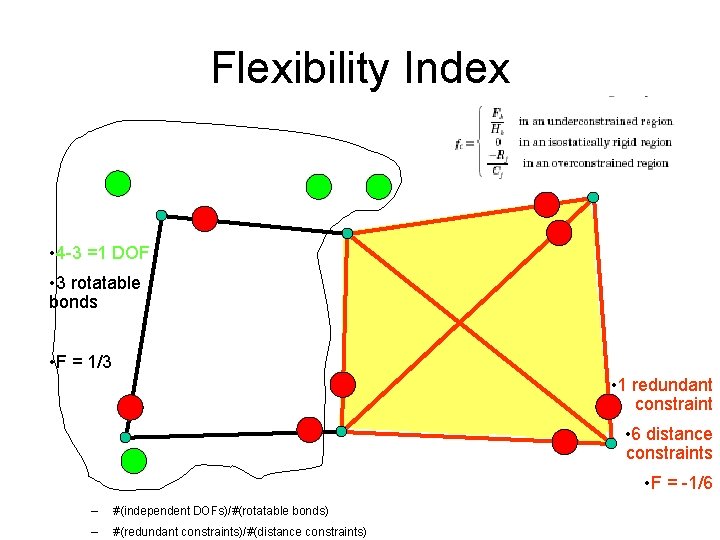
Flexibility Index • 4 -3 =1 DOF • 3 rotatable bonds • F = 1/3 • 1 redundant constraint • 6 distance constraints • F = -1/6 – #(independent DOFs)/#(rotatable bonds) – #(redundant constraints)/#(distance constraints)

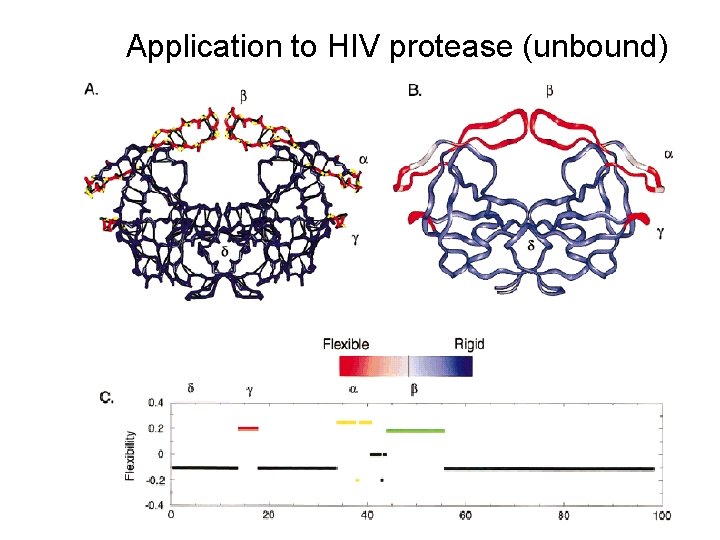
Application to HIV protease (unbound)

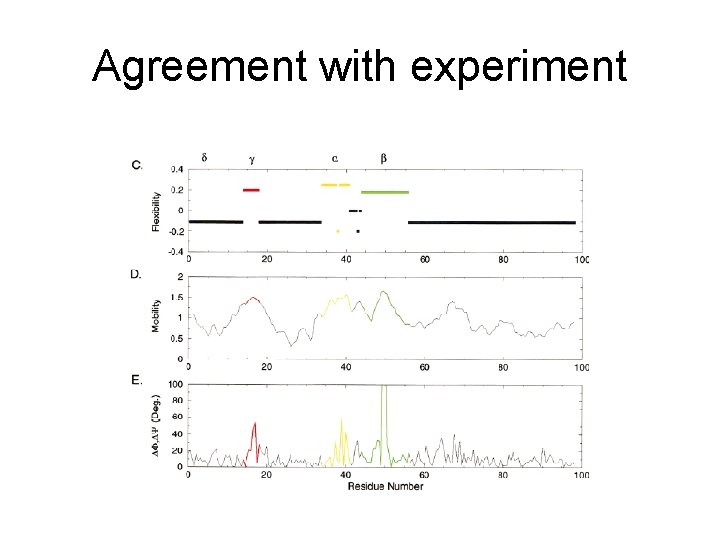
Agreement with experiment

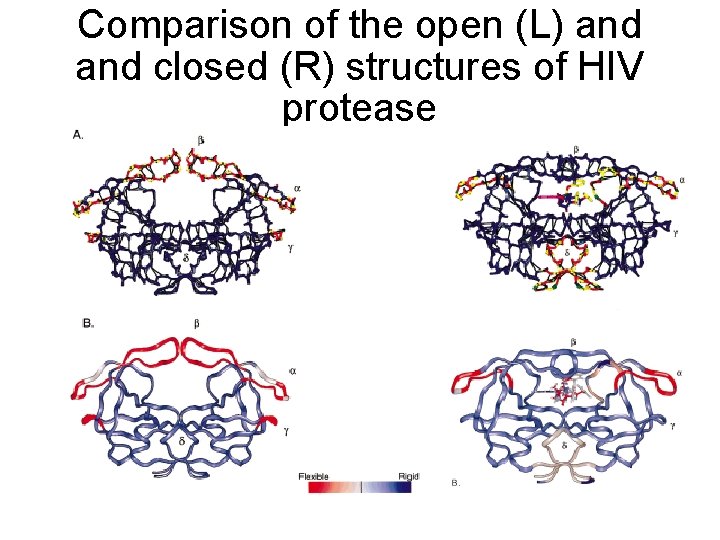
Comparison of the open (L) and closed (R) structures of HIV protease

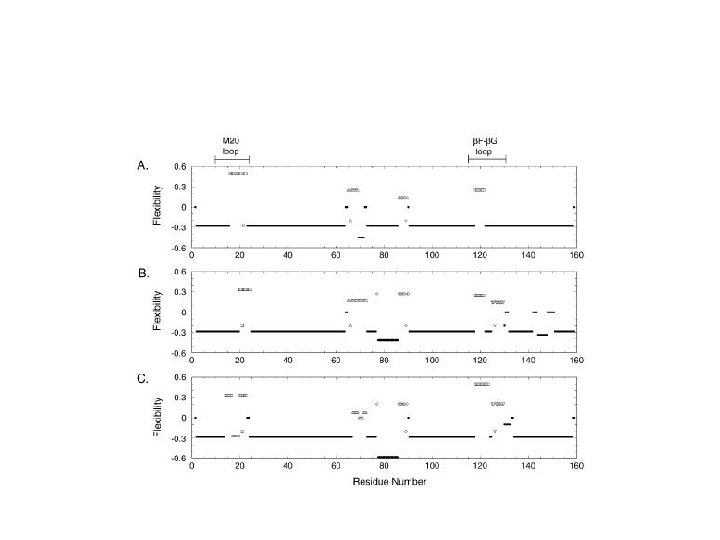
Dihydrofolate reductase

Rigid cluster decomposition barnase Maltodextrin binding protein Gohlke and Thorpe. Biophysical Journal 91: 2115 -2120 (2006)

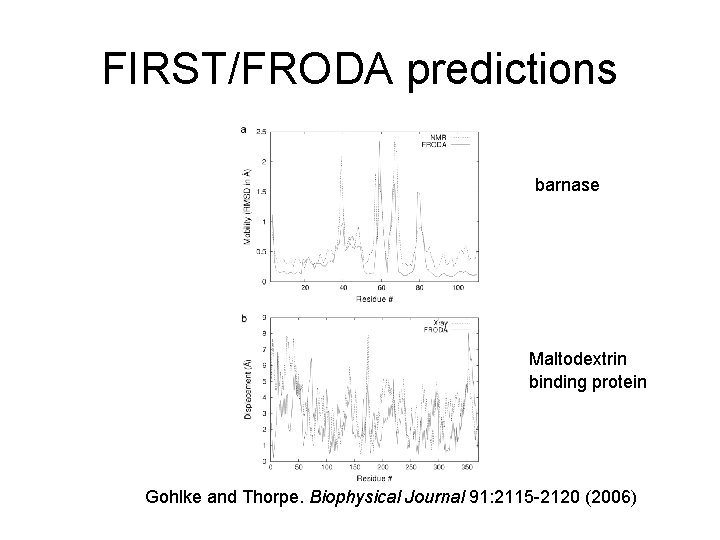
FIRST/FRODA predictions barnase Maltodextrin binding protein Gohlke and Thorpe. Biophysical Journal 91: 2115 -2120 (2006)

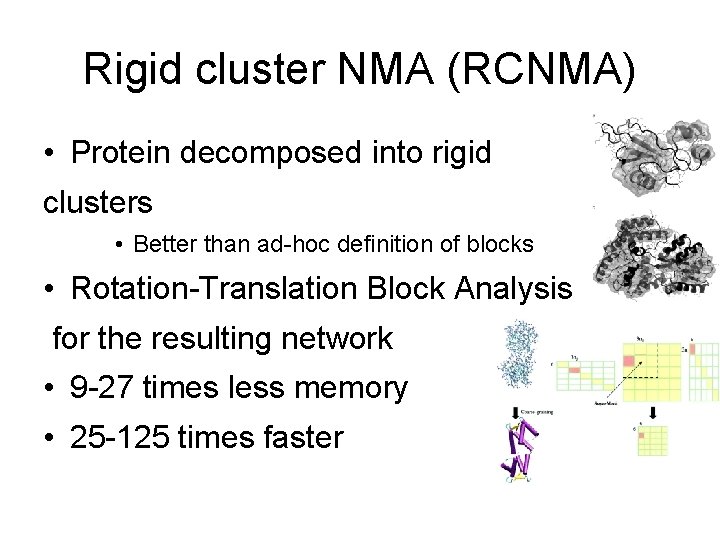
Rigid cluster NMA (RCNMA) • Protein decomposed into rigid clusters • Better than ad-hoc definition of blocks • Rotation-Translation Block Analysis for the resulting network • 9 -27 times less memory • 25 -125 times faster

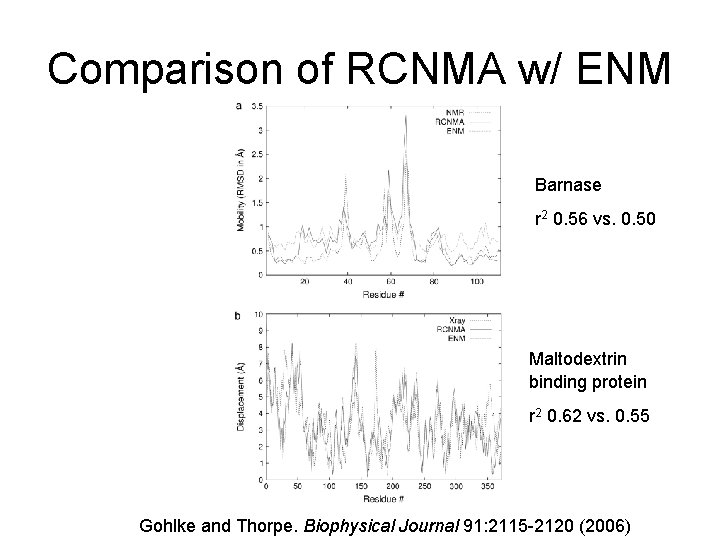
Comparison of RCNMA w/ ENM Barnase r 2 0. 56 vs. 0. 50 Maltodextrin binding protein r 2 0. 62 vs. 0. 55 Gohlke and Thorpe. Biophysical Journal 91: 2115 -2120 (2006)

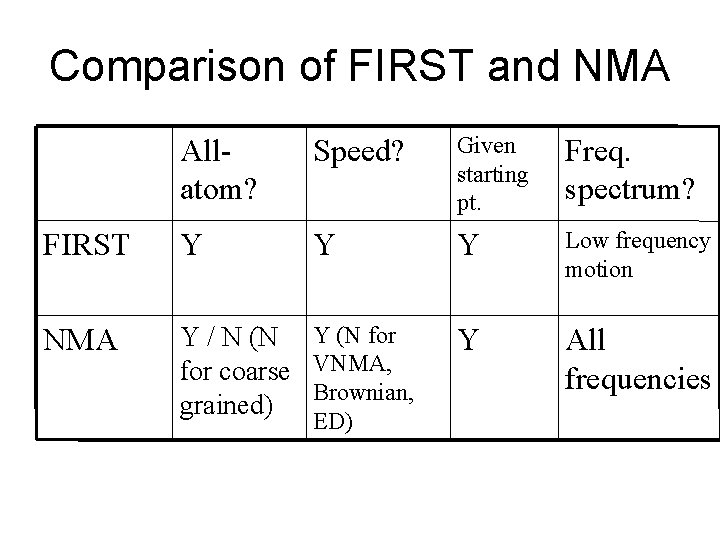
Comparison of FIRST and NMA Allatom? Speed? Given starting pt. Freq. spectrum? FIRST Y Y Y Low frequency motion NMA Y / N (N Y (N for coarse VNMA, grained) Brownian, Y All frequencies ED)

Comparison of FIRST and NMA (2) Way of generating new conformations? Flexibility/mobili ty index FIRST Y (with ROCK or Y* FRODA) NMA Y Y *: incorrect for rigid regions flanked by flexible hinges

http: //flexweb. asu. edu

Conclusion • • • Rigidity theory Constraint counting Based on a single structure Fast Available on the web: http: //flexweb. asu. edu • Tools using FIRST to generate new conformations: ROCK, FRODA