Normal Forms for Contextfree Grammars 1 Chomsky Normal

Normal Forms for Context-free Grammars 1

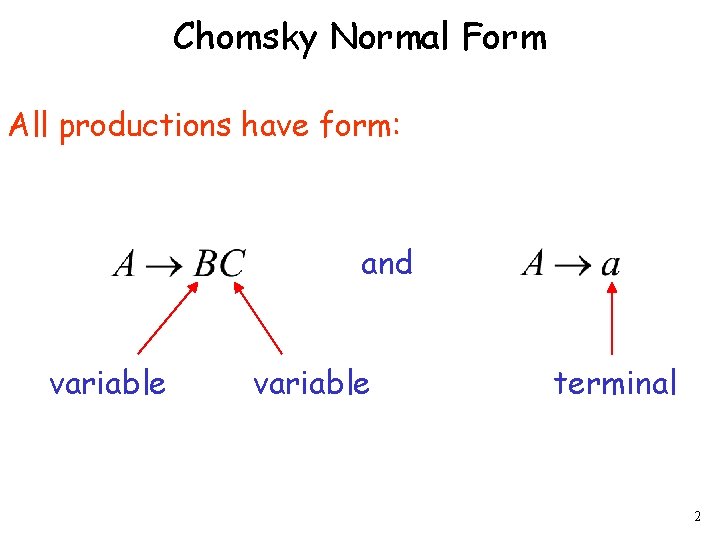
Chomsky Normal Form All productions have form: and variable terminal 2

Examples: Chomsky Normal Form Not Chomsky Normal Form 3

Convertion to Chomsky Normal Form Example: Not Chomsky Normal Form 4

Introduce variables for terminals: 5

Introduce intermediate variable: 6

Introduce intermediate variable: 7

Final grammar in Chomsky Normal Form: Initial grammar 8

In general: From any context-free grammar not in Chomsky Normal Form we can obtain: An equivalent grammar in Chomsky Normal Form 9

The Procedure First remove: Nullable variables Unit productions 10

For every symbol : Add production In productions: replace with New variable: 11

Replace any production with New intermediate variables: 12

Theorem: For any context-free grammar there is an equivalent grammar in Chomsky Normal Form 13

Observations • Chomsky normal forms are good for parsing and proving theorems • It is very easy to find the Chomsky normal form of any context-free grammar 14

Greinbach Normal Form All productions have form: symbol variables 15

Examples: Greinbach Normal Form Not Greinbach Normal Form 16

Conversion to Greinbach Normal Form: Greinbach Normal Form 17

Theorem: For any context-free grammar there is an equivalent grammar in Greinbach Normal Form 18

Observations • Greinbach normal forms are very good for parsing • It is hard to find the Greinbach normal form of any context-free grammar 19

An Application of Chomsky Normal Forms 20

The CYK Membership Algorithm Input: • Grammar in Chomsky Normal Form • String Output: find if 21

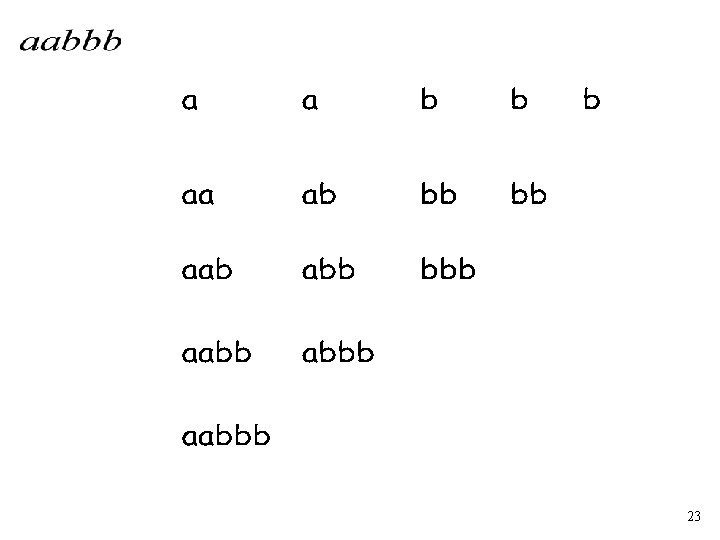
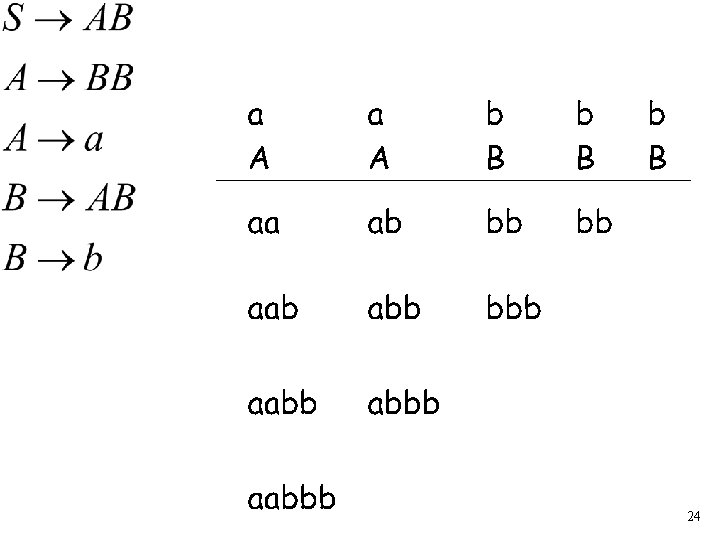
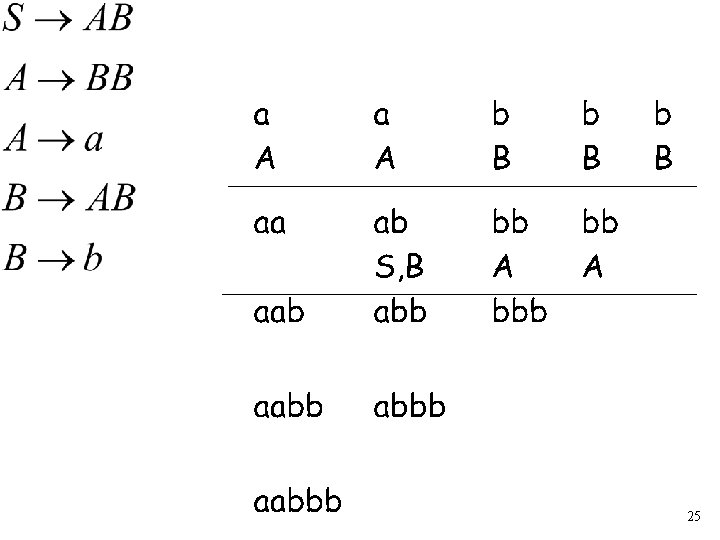
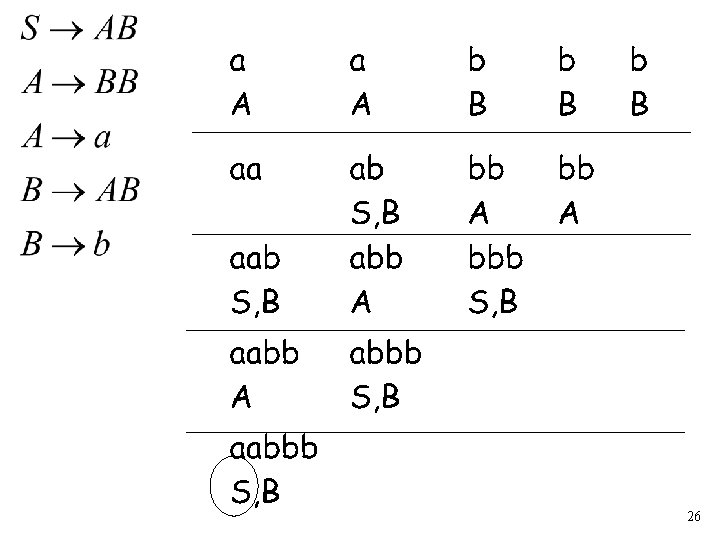
The Algorithm Input example: • Grammar • String : : 22

23

24

25

26

Therefore: Time Complexity: Observation: The CYK algorithm can be easily converted to a parser 27

Pushdown Automata PDAs 28

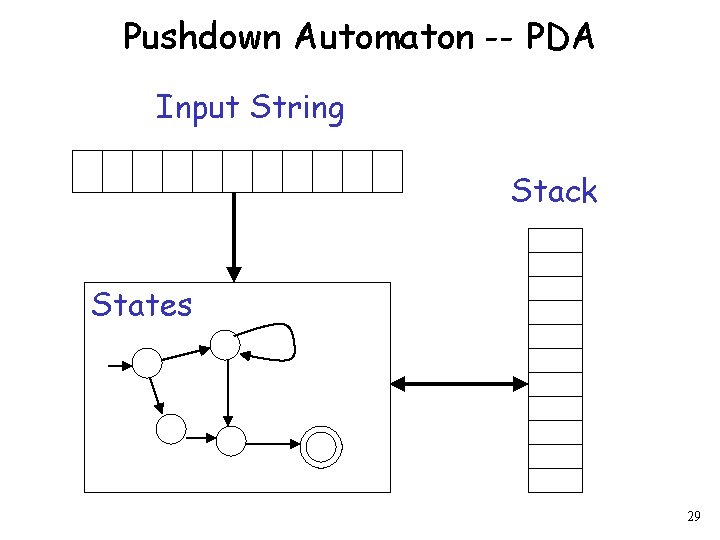
Pushdown Automaton -- PDA Input String Stack States 29

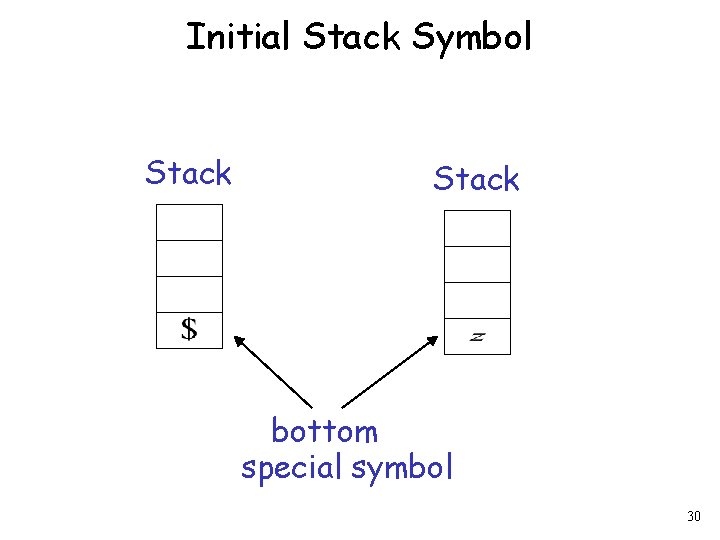
Initial Stack Symbol Stack bottom special symbol 30

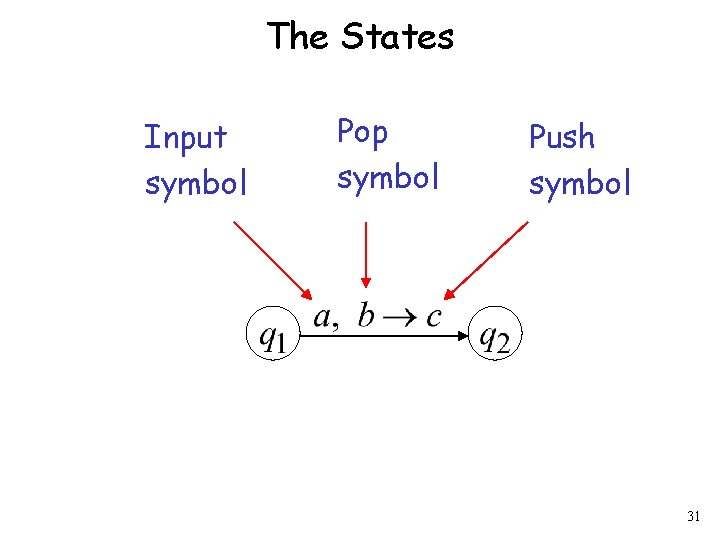
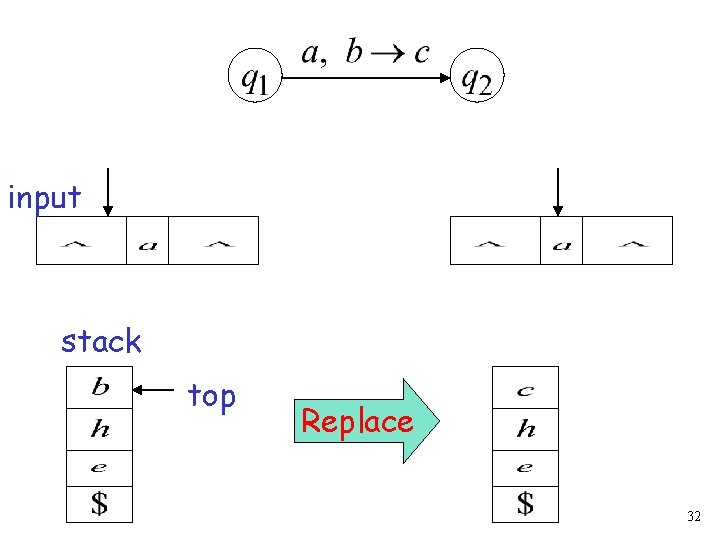
The States Input symbol Pop symbol Push symbol 31

input stack top Replace 32

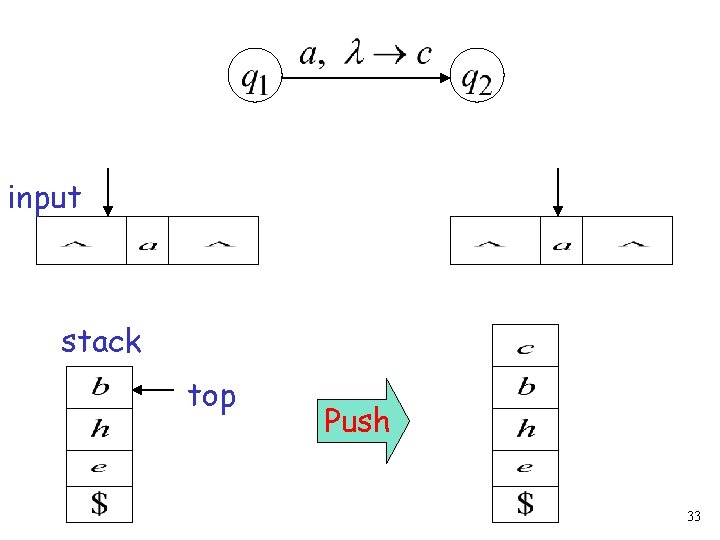
input stack top Push 33

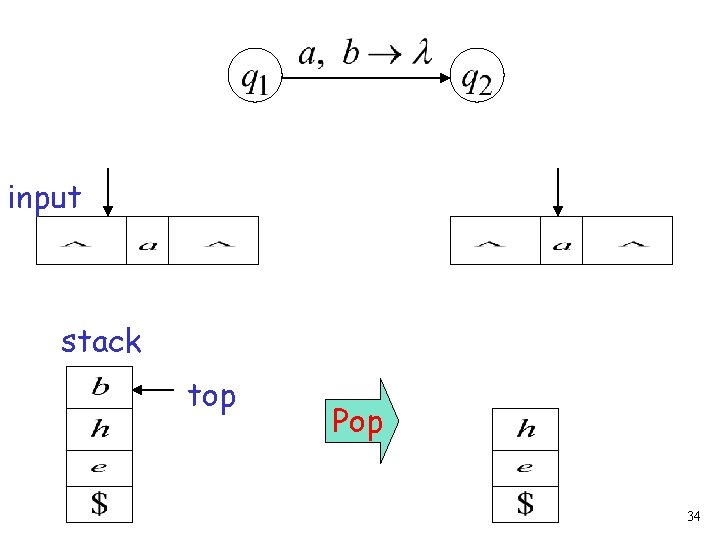
input stack top Pop 34

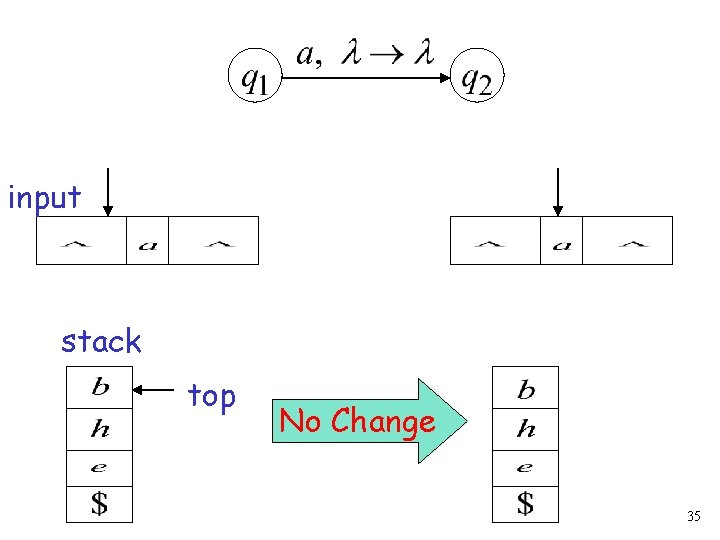
input stack top No Change 35

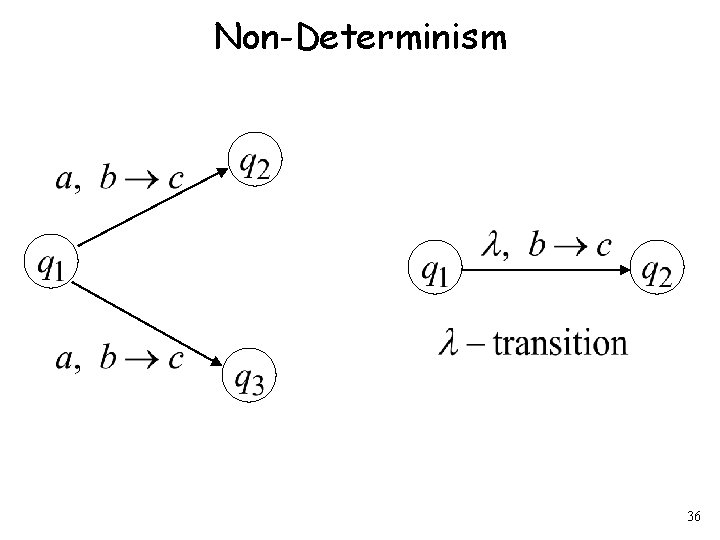
Non-Determinism 36

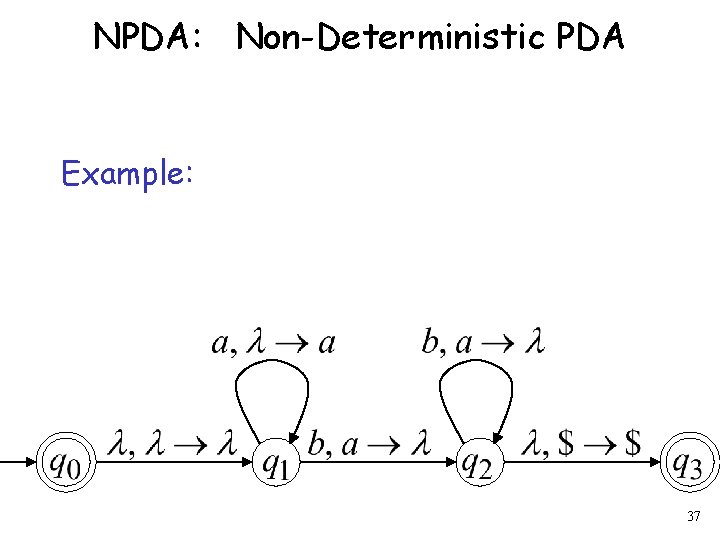
NPDA: Non-Deterministic PDA Example: 37

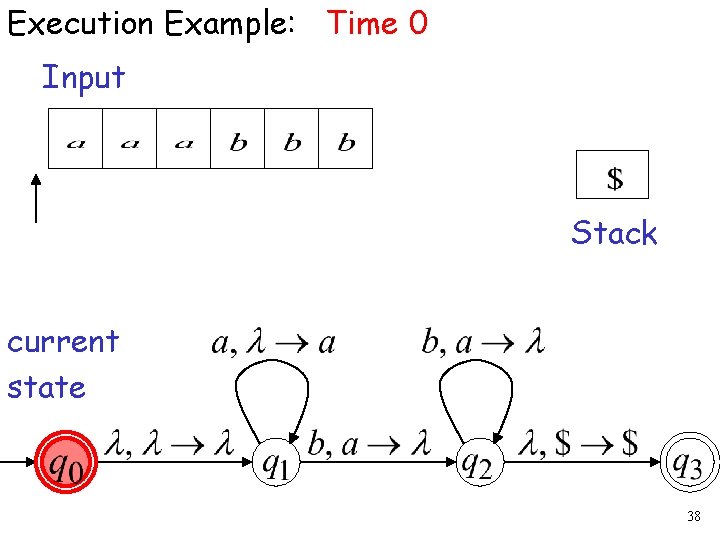
Execution Example: Time 0 Input Stack current state 38

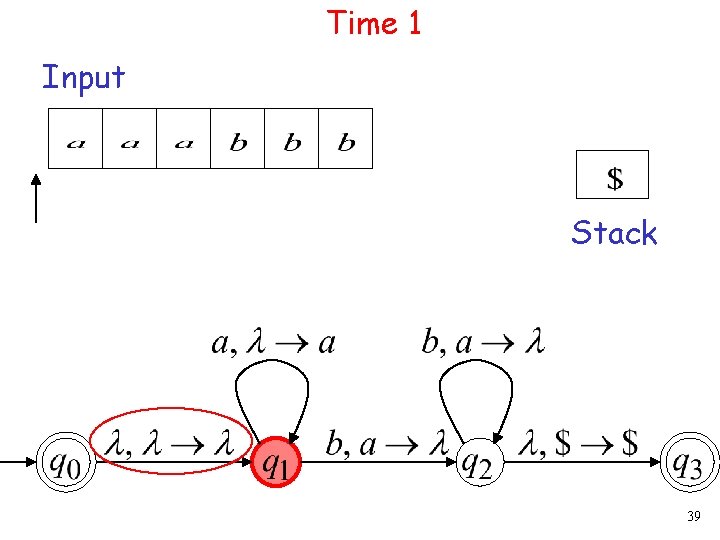
Time 1 Input Stack 39

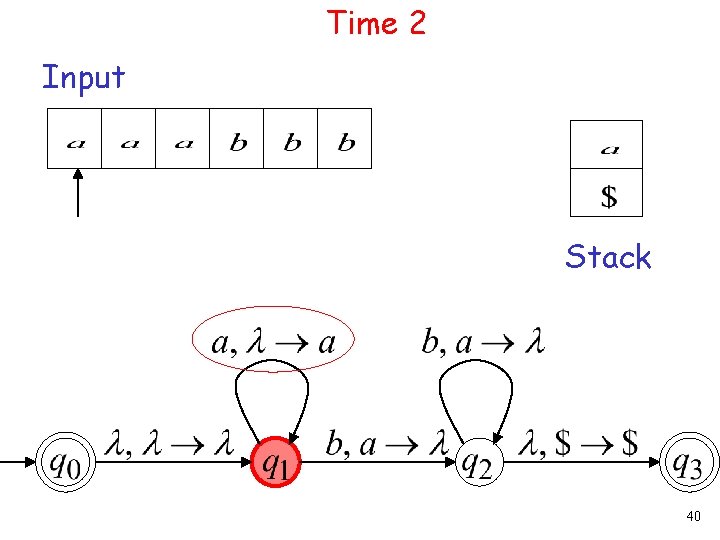
Time 2 Input Stack 40

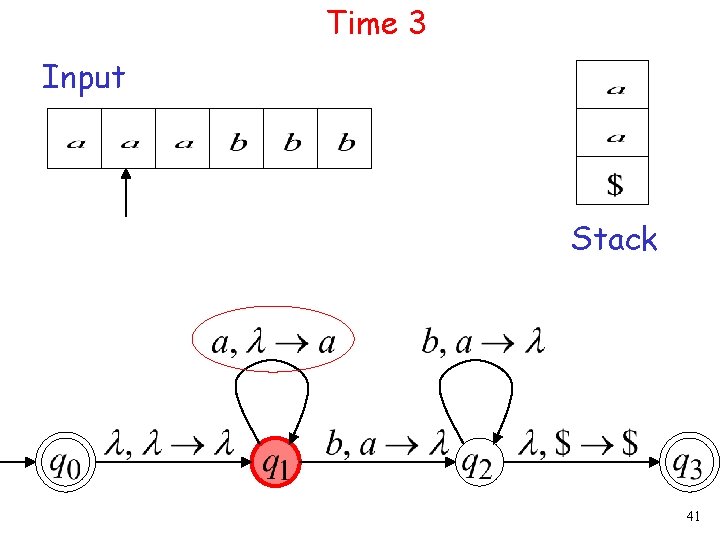
Time 3 Input Stack 41

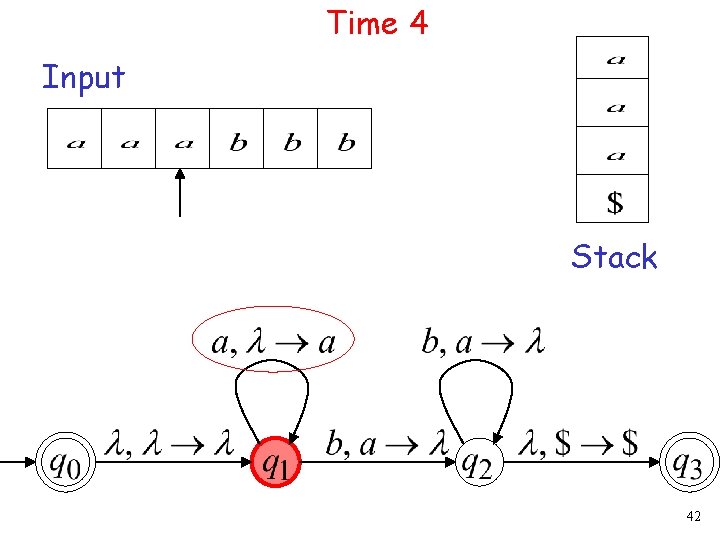
Time 4 Input Stack 42

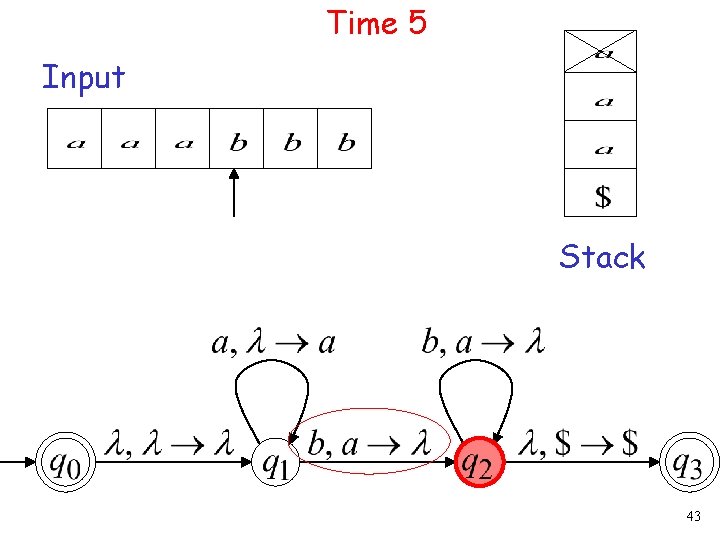
Time 5 Input Stack 43

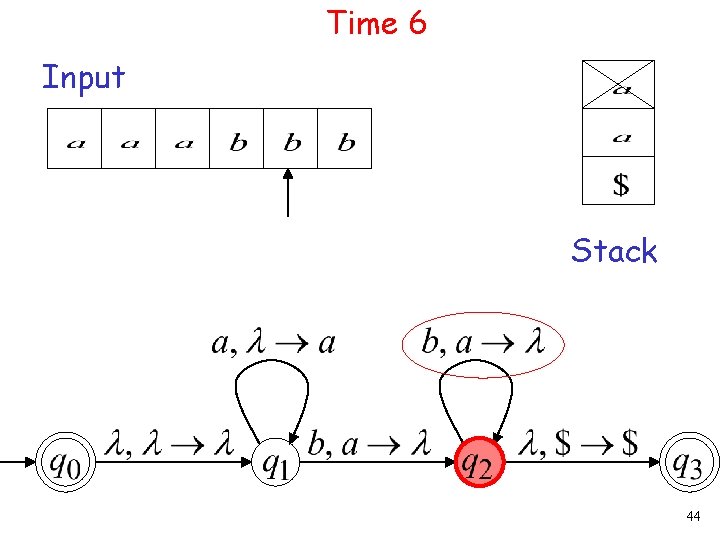
Time 6 Input Stack 44

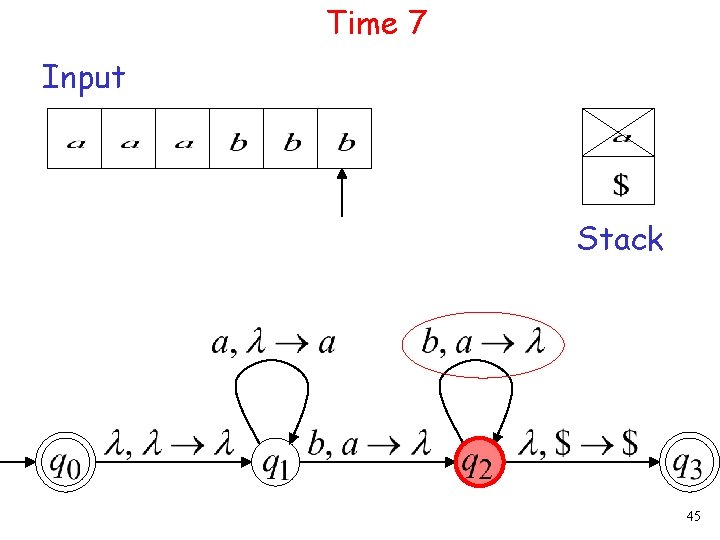
Time 7 Input Stack 45

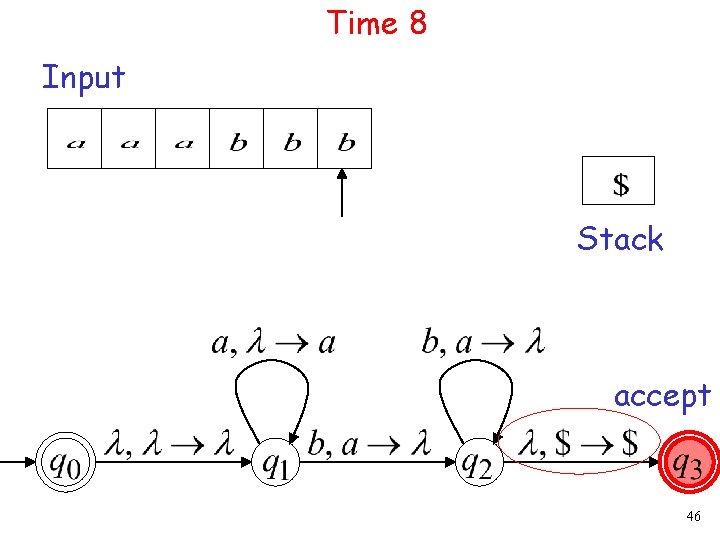
Time 8 Input Stack accept 46

A string is accepted if: • All the input is consumed • The last state is a final state We do not care about the stack contents 47

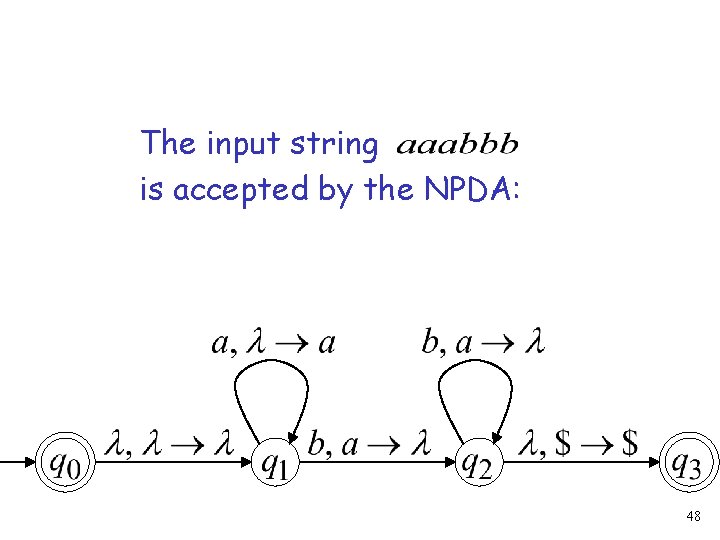
The input string is accepted by the NPDA: 48

In general, is the language accepted by the NPDA: 49

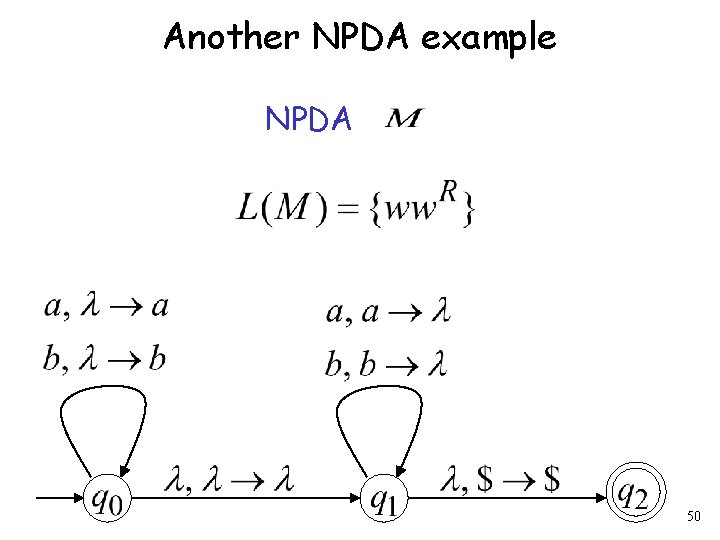
Another NPDA example NPDA 50

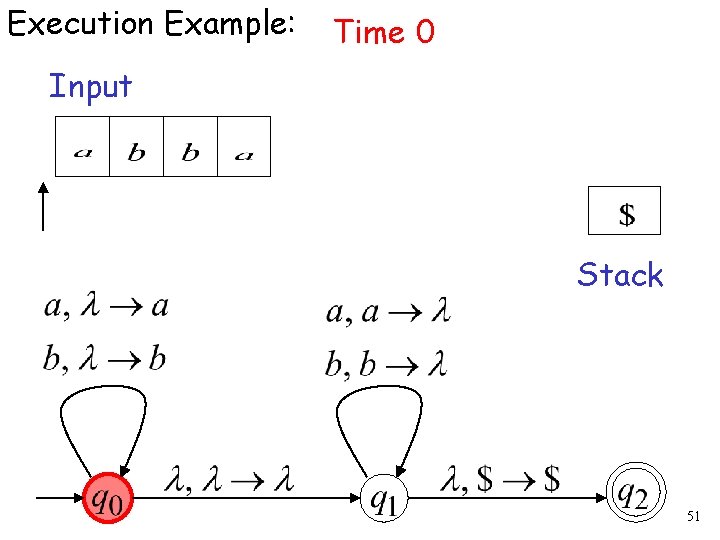
Execution Example: Time 0 Input Stack 51

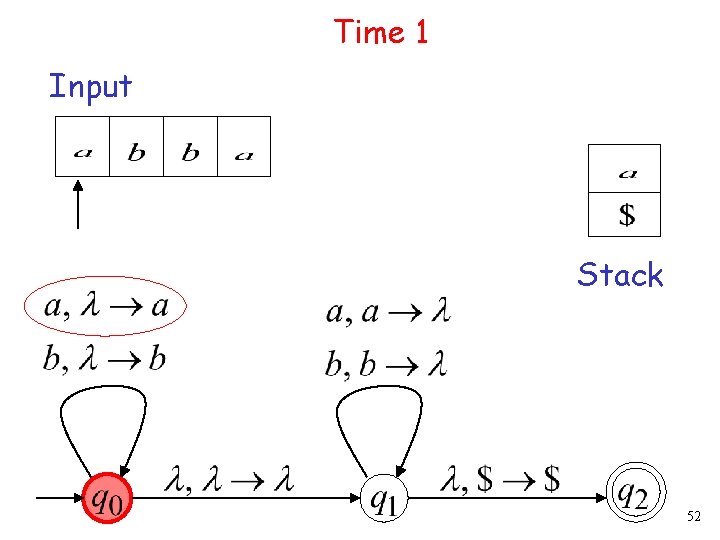
Time 1 Input Stack 52

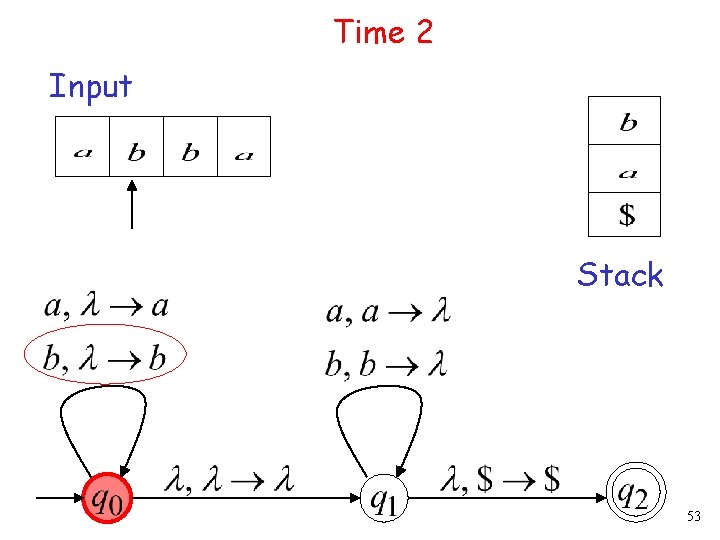
Time 2 Input Stack 53

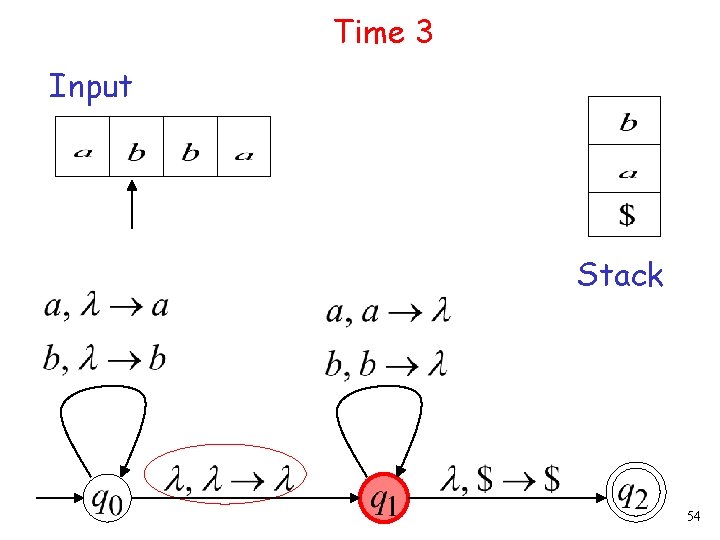
Time 3 Input Stack 54

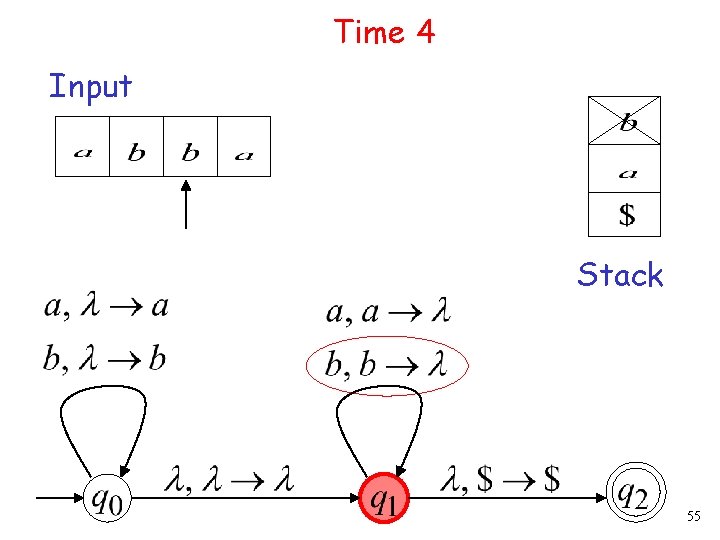
Time 4 Input Stack 55

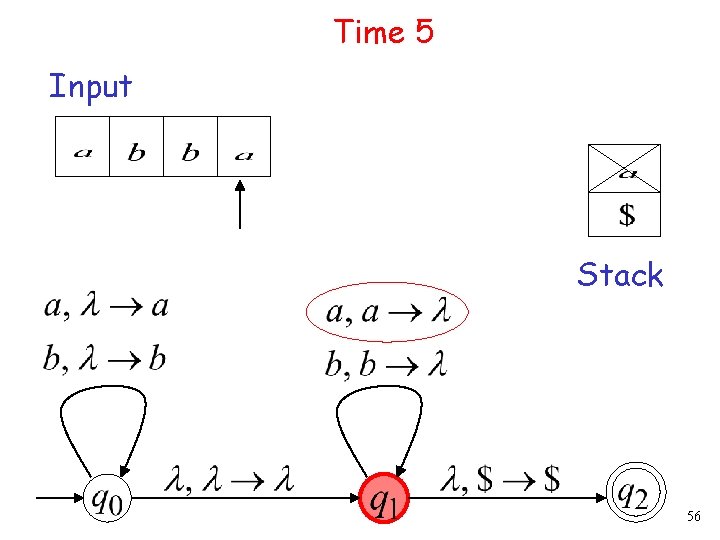
Time 5 Input Stack 56

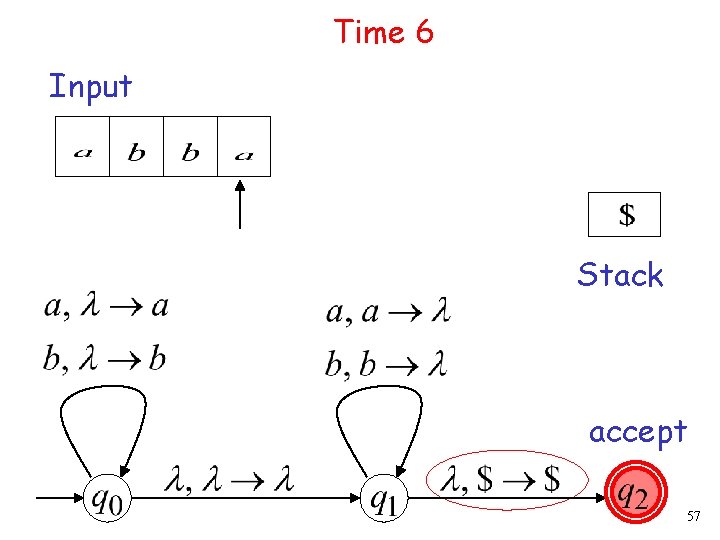
Time 6 Input Stack accept 57