Normal Distributions Z Transformations Central Limit Theorem Standard

Normal Distributions Z Transformations Central Limit Theorem Standard Normal Distribution Z Distribution Table Confidence Intervals Levels of Significance Critical Values Population Parameter Estimations
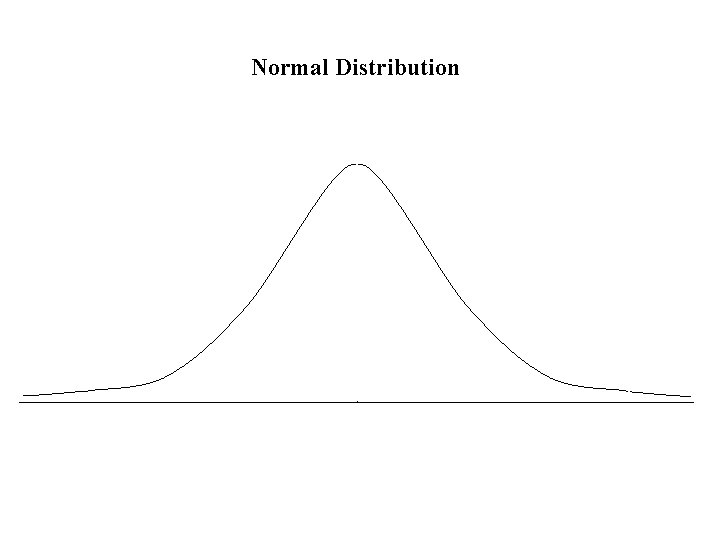
Normal Distribution
Normal Distribution Mean m
Normal Distribution Mean m Variance s 2
Normal Distribution Mean m Variance s 2 Standard Deviation s
Normal Distribution Mean m Variance s 2 Standard Deviation s Z Transformation
Normal Distribution Mean m Variance s 2 Standard Deviation s Pick any point X along the abscissa.
Normal Distribution Mean m Variance s 2 Standard Deviation s x
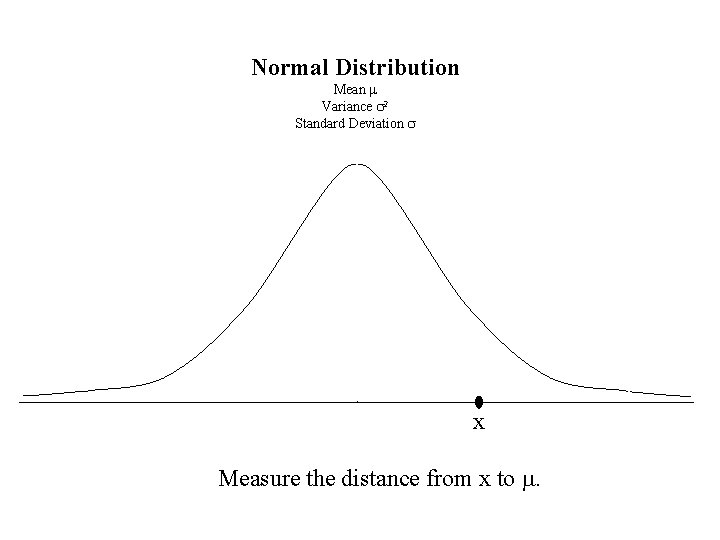
Normal Distribution Mean m Variance s 2 Standard Deviation s x Measure the distance from x to m.
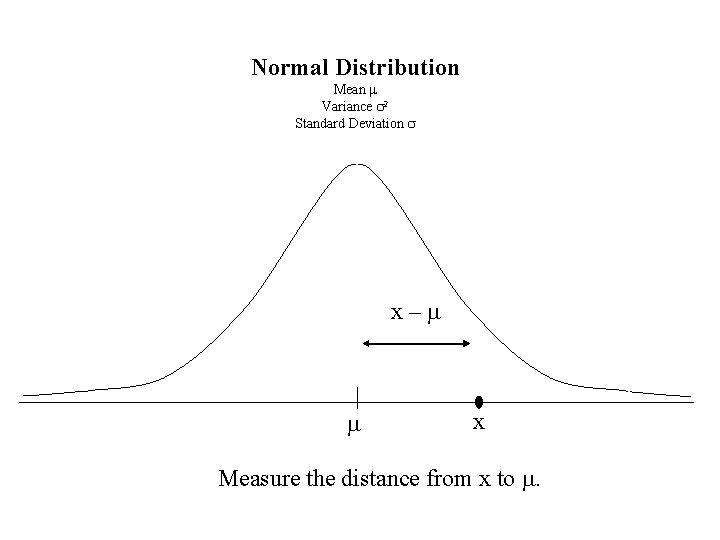
Normal Distribution Mean m Variance s 2 Standard Deviation s x–m m x Measure the distance from x to m.
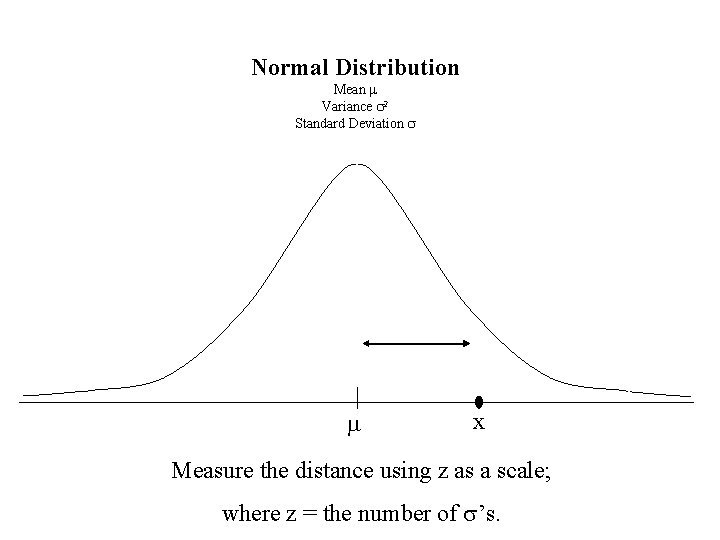
Normal Distribution Mean m Variance s 2 Standard Deviation s m x Measure the distance using z as a scale; where z = the number of s’s.
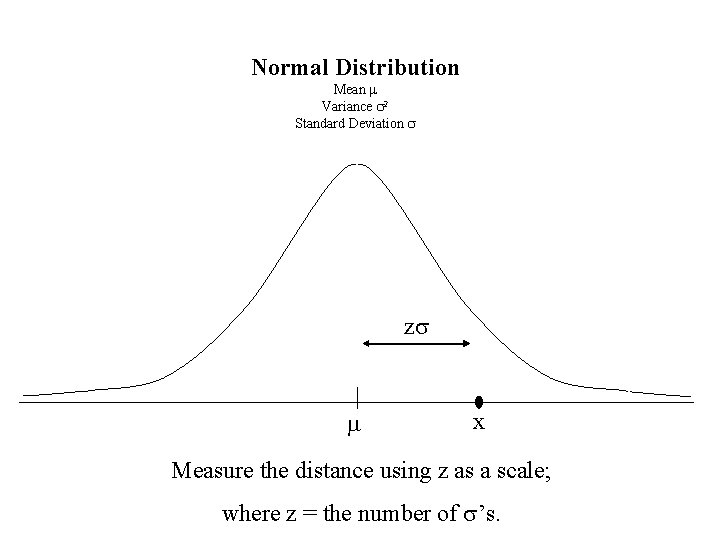
Normal Distribution Mean m Variance s 2 Standard Deviation s zs m x Measure the distance using z as a scale; where z = the number of s’s.
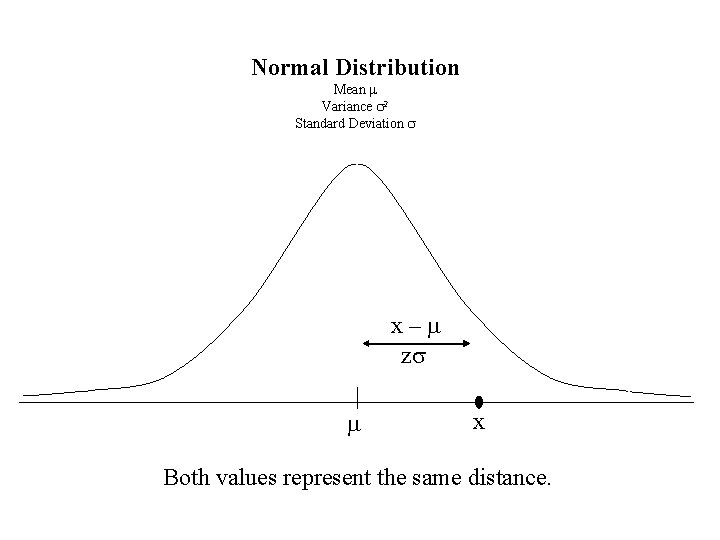
Normal Distribution Mean m Variance s 2 Standard Deviation s x–m zs m x Both values represent the same distance.
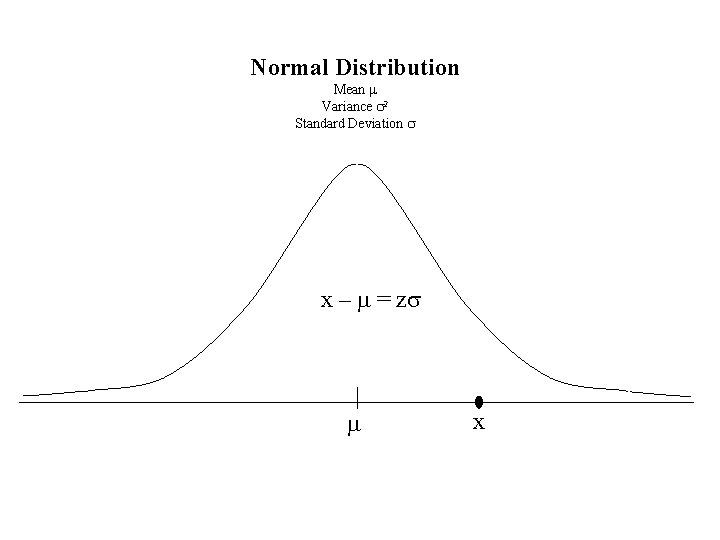
Normal Distribution Mean m Variance s 2 Standard Deviation s x – m = zs m x

Normal Distribution Mean m Variance s 2 Standard Deviation s x – m = zs z = (x – m) / s m x

Z Transformation for Normal Distribution Z=(x–m)/s

Central Limit Theorem • The distribution of all sample means of sample size n from a Normal Distribution (m, s 2) is a normally distributed with Mean = m Variance = s 2 / n Standard Error = s / √n

Sampling Normal Distribution Sample Size n Mean m Variance s 2/ n Standard Error s / √n m
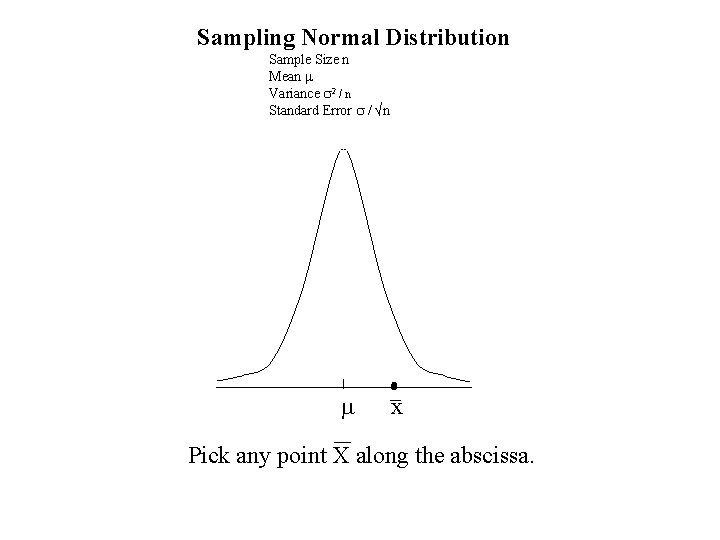
Sampling Normal Distribution Sample Size n Mean m Variance s 2 / n Standard Error s / √n m x Pick any point X along the abscissa.
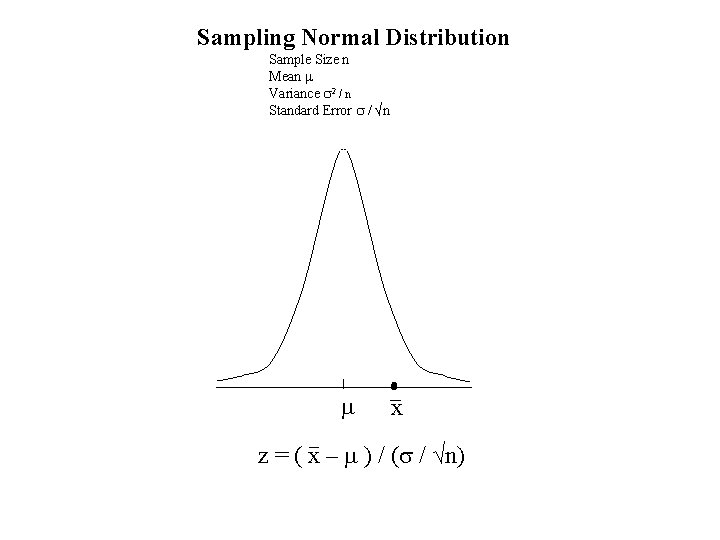
Sampling Normal Distribution Sample Size n Mean m Variance s 2 / n Standard Error s / √n m x z = ( x – m ) / (s / √n)

Z Transformation for Sampling Distribution Z = ( x – m ) / (s / √n)
Standard Normal Distribution & The Z Distribution Table What is a Standard Normal Distribution?

Standard Normal Distribution Mean m = 0
Standard Normal Distribution Mean m = 0 Variance s 2 = 1
Standard Normal Distribution Mean m = 0 Variance s 2 = 1 Standard Deviation s = 1
Standard Normal Distribution Mean m = 0 Variance s 2 = 1 Standard Deviation s = 1 What is the Z Distribution Table?

Z Distribution Table • The Z Distribution Table is a numeric tabulation of the Cumulative Probability Values of the Standard Normal Distribution.

Z Distribution Table • The Z Distribution Table is a numeric tabulation of the Cumulative Probability Values of the Standard Normal Distribution. What is “Z” ?

What is “Z” ? Define Z as the number of standard deviations along the abscissa. Practically speaking, Z ranges from -4. 00 to +4. 00 F(-4. 00) = 0. 00003 and F(+4. 00) = 0. 99997
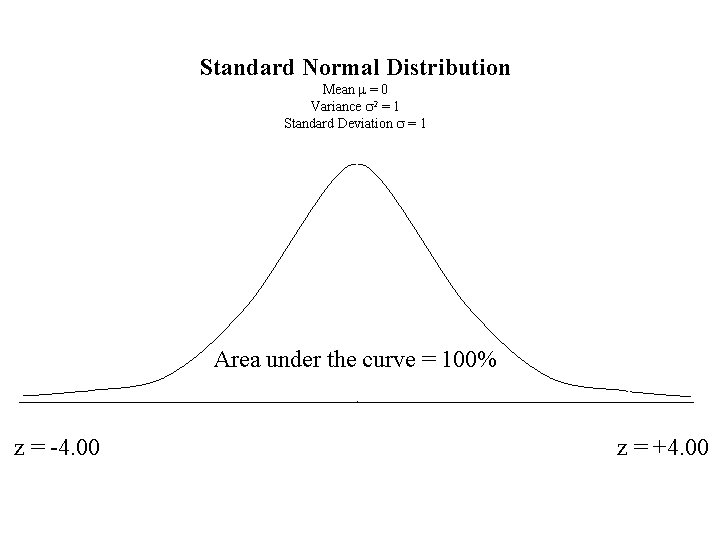
Standard Normal Distribution Mean m = 0 Variance s 2 = 1 Standard Deviation s = 1 Area under the curve = 100% z = -4. 00 z = +4. 00
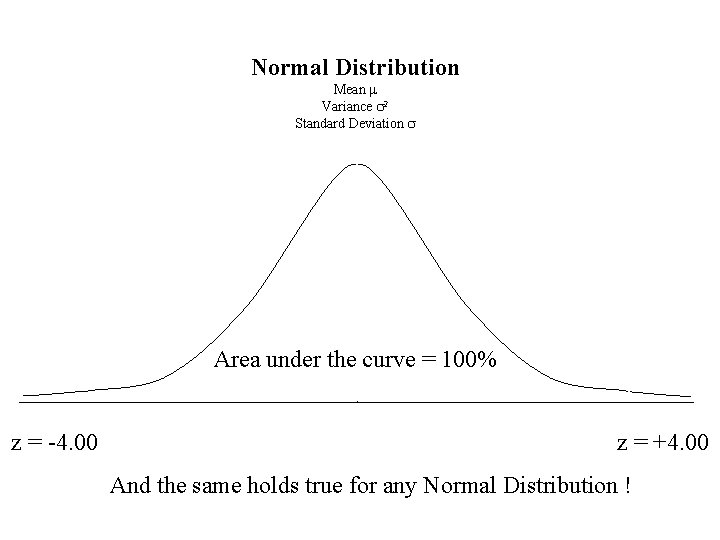
Normal Distribution Mean m Variance s 2 Standard Deviation s Area under the curve = 100% z = -4. 00 z = +4. 00 And the same holds true for any Normal Distribution !
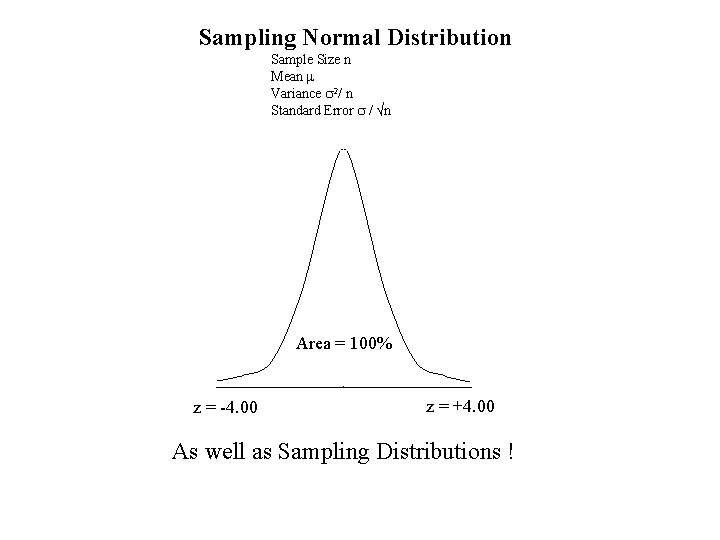
Sampling Normal Distribution Sample Size n Mean m Variance s 2/ n Standard Error s / √n Area = 100% z = -4. 00 z = +4. 00 As well as Sampling Distributions !

Confidence Intervals Levels of Significance Critical Values

Confidence Intervals • Example: Select the middle 95% of the area under a normal distribution curve.
Confidence Interval 95%
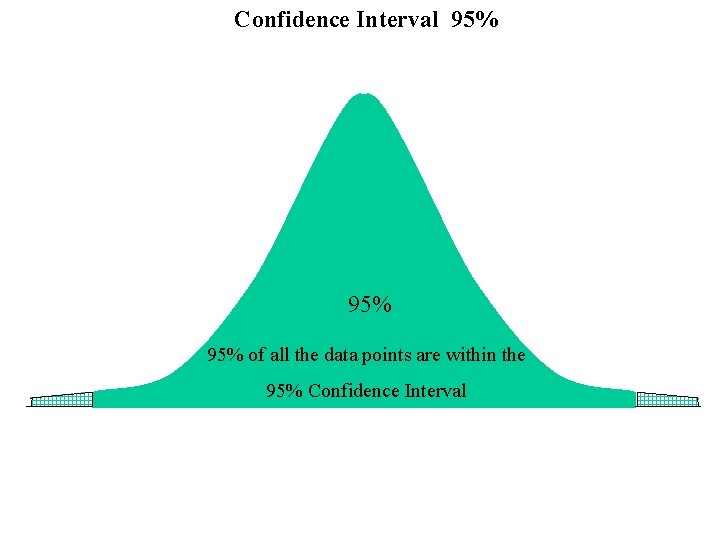
Confidence Interval 95% 95% of all the data points are within the 95% Confidence Interval
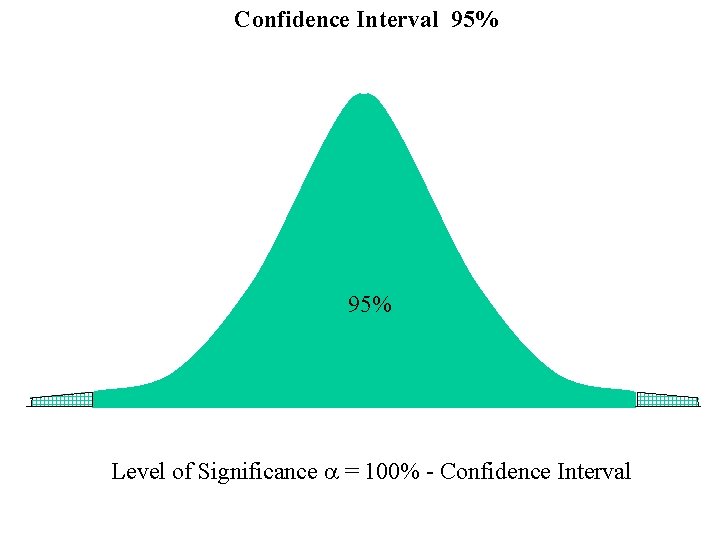
Confidence Interval 95% Level of Significance a = 100% - Confidence Interval
Confidence Interval 95% Level of Significance a = 100% - Confidence Interval a = 100% - 95% = 5%

Confidence Interval 95% Level of Significance a = 100% - Confidence Interval a= 100% - 95% = 5% a/2 = 2. 5%
Confidence Interval 95% Level of Significance a = 5% a / 2 = 2. 5%
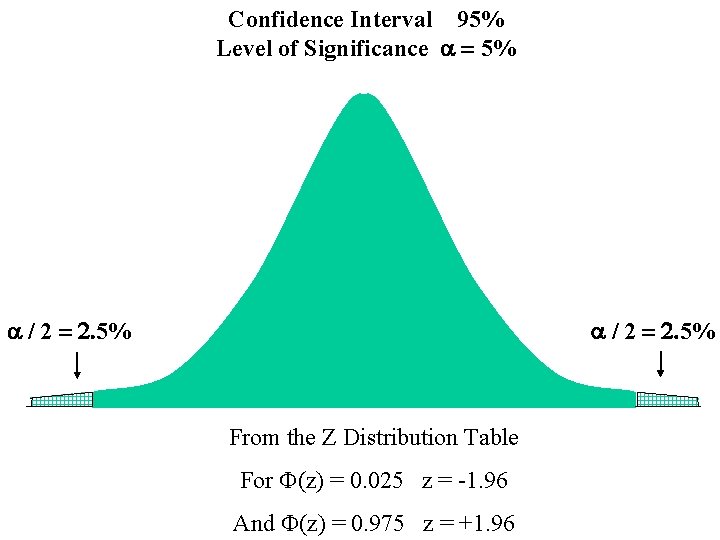
Confidence Interval 95% Level of Significance a = 5% a / 2 = 2. 5% From the Z Distribution Table For F(z) = 0. 025 z = -1. 96 And F(z) = 0. 975 z = +1. 96
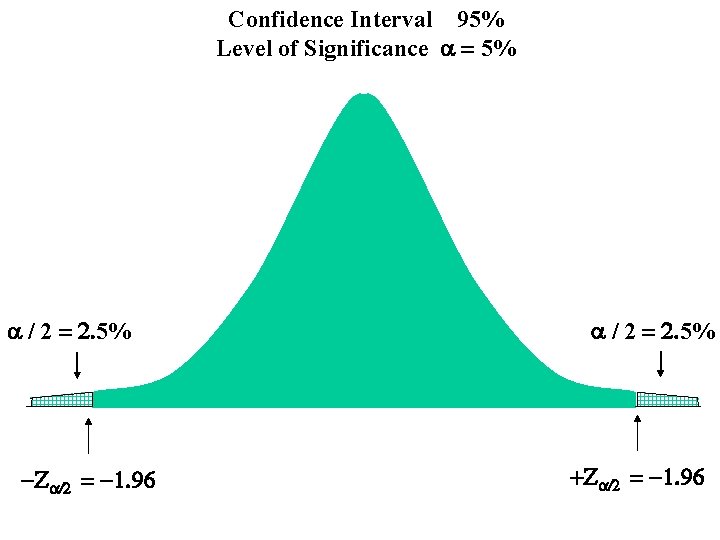
Confidence Interval 95% Level of Significance a = 5% a / 2 = 2. 5% -Za/2 = -1. 96 a / 2 = 2. 5% +Za/2 = -1. 96

Calculating X Critical Values X critical values are the lower and upper bounds of the samples means for a given confidence interval. For the 95% Confidence Interval X lower = (m - X) Za/2 / ( s / √n) where Za/2 = -1. 96 X upper = (m - X) Za/2 / ( s / √n) where Za/2 = +1. 96
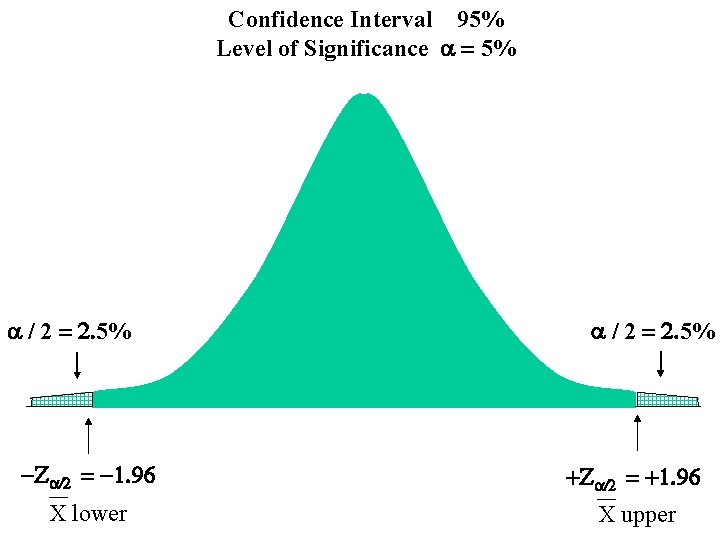
Confidence Interval 95% Level of Significance a = 5% a / 2 = 2. 5% -Za/2 = -1. 96 +Za/2 = +1. 96 X lower X upper

Estimating Population Parameters Using Sample Data

Estimating Population Parameters Using Sample Data A very robust estimate for the population variance is s 2 = s 2. A Point Estimate for the population mean is m = X. Add a Margin of Error about the Mean by including a Confidence Interval about the point estimate. From Z = ( X – m ) / (s / √n) m = X ± Za/2 (s / √n) For 95%, Za/2 = ± 1. 96
- Slides: 46