Normal Distributions EDA Steps Univariate EDA Graphically Numerically

Normal Distributions

EDA Steps • Univariate EDA – Graphically – Numerically – Model Normal Distributions Slide #2

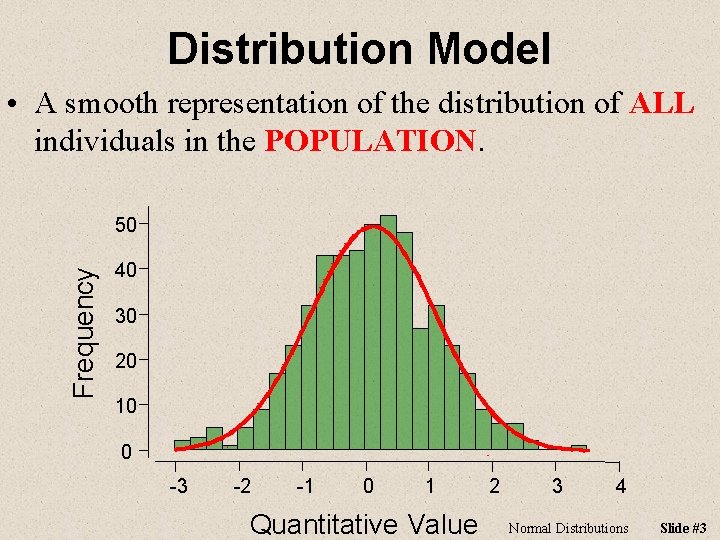
Distribution Model • A smooth representation of the distribution of ALL individuals in the POPULATION. Frequency 50 40 30 20 10 0 -3 -2 -1 0 1 Quantitative Value 2 3 4 Normal Distributions Slide #3

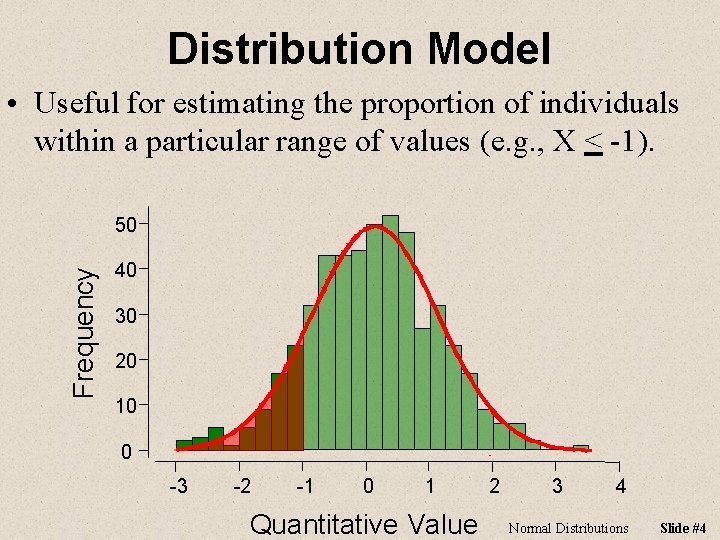
Distribution Model • Useful for estimating the proportion of individuals within a particular range of values (e. g. , X < -1). Frequency 50 40 30 20 10 0 -3 -2 -1 0 1 Quantitative Value 2 3 4 Normal Distributions Slide #4

1. What is the generic center and dispersion of any normal distribution? 2. What is the exact center of a N(10, 4)? 3. What is the exact dispersion of a N(10, 4)? Normal Distributions Slide #5

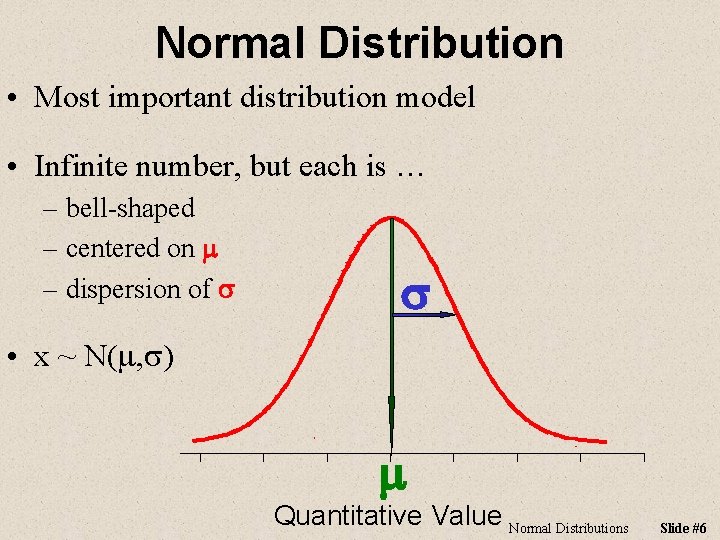
Normal Distribution • Most important distribution model • Infinite number, but each is … – bell-shaped – centered on m – dispersion of s s • x ~ N(m, s) m Quantitative Value Normal Distributions Slide #6

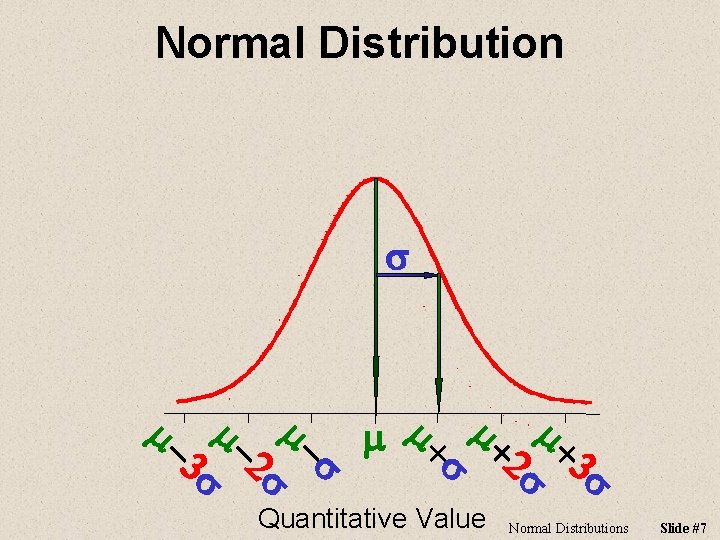
Normal Distribution s s Quantitative Value 3 s m+ 2 s m+ m+ s m 2 s m 3 s m- m Normal Distributions Slide #7

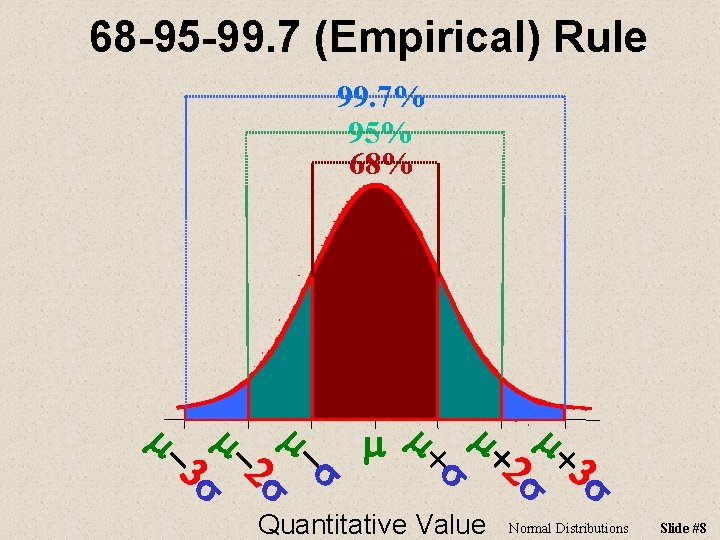
68 -95 -99. 7 (Empirical) Rule 99. 7% 95% 68% s Quantitative Value 3 s m+ 2 s m+ m+ s m 2 s m 3 s m- m Normal Distributions Slide #8

1. What percentage of individuals are between m+2 s? 2. What percentage of individuals are between m+1 s? 3. What percentage of individuals are between 6 and 14 on a N(10, 4)? 4. What percentage of individuals are between -2 and 22 on a N(10, 4)? Normal Distributions Slide #9

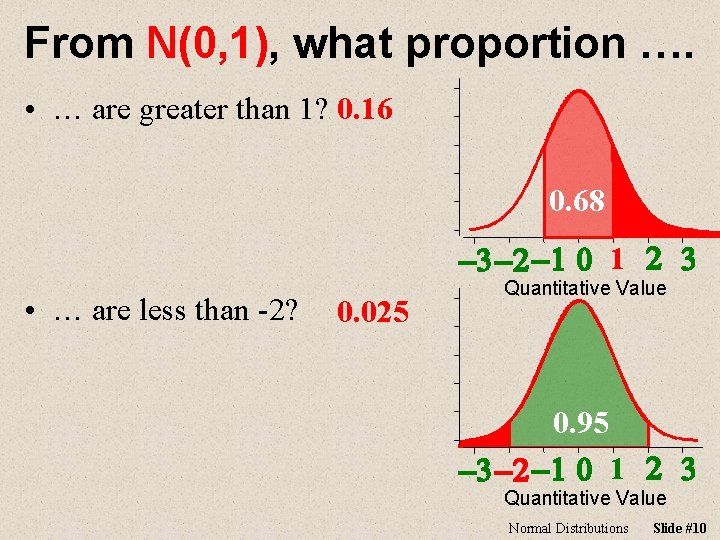
From N(0, 1), what proportion …. • … are greater than 1? 0. 16 0. 68 -3 -2 -1 0 1 2 3 • … are less than -2? 0. 025 Quantitative Value 0. 95 -3 -2 -1 0 1 2 3 Quantitative Value Normal Distributions Slide #10

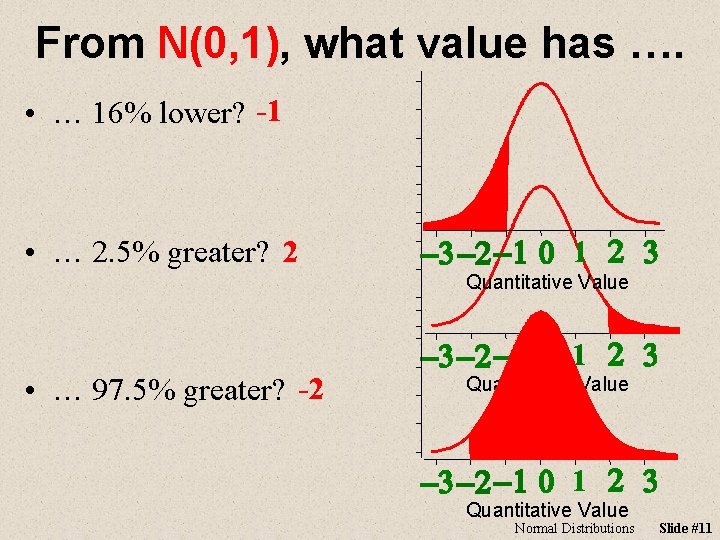
From N(0, 1), what value has …. • … 16% lower? -1 • … 2. 5% greater? 2 -3 -2 -1 0 1 2 3 Quantitative Value • … 97. 5% greater? -2 -3 -2 -1 0 1 2 3 Quantitative Value Normal Distributions Slide #11

1. What percentage of individuals are greater than 10 on a N(5, 5) distribution? 2. What percentage of individuals are less than 4 on a N(10, 3) distribution? 3. What is the value from a N(7, 3) that has 16% of the individuals larger? 4. What is the value from a N(7, 3) that has 2. 5% of the individuals smaller? Normal Distributions Slide #12

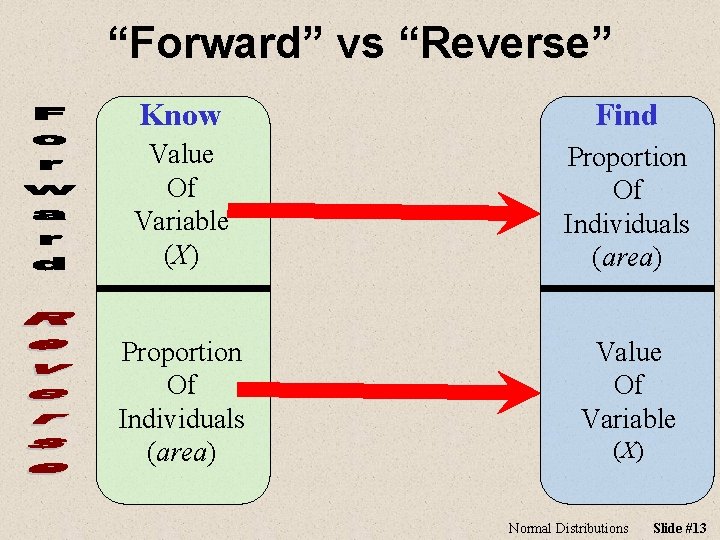
“Forward” vs “Reverse” Know Find Value Of Variable (X) Proportion Of Individuals (area) Value Of Variable (X) Normal Distributions Slide #13

What Type Of Question? 1. What proportion of students will score between 70 and 90 on the next exam? 2. What is the test score such that the 15% of the students score higher? 3. What is the gas mileage that has 25% of the cars lower? 4. What proportion of cars get more than 20 mpg? 5. What are the two heights that contain the most common 50% of professor’s heights? Forward Between Reverse – Right of Reverse – Left of Forward Right of Reverse Between Normal Distributions Slide #14

Suppose that the distribution of number of carpenter ants in a nest is N(1400, 300). 1. What is an individual? 2. What is the variable? 3. What type of variable is that? 4. What is m? 5. What is s? 6. Draw the distribution with an appropriate axis scale and label. Normal Distributions Slide #15

Determine what type of calculation is required. 1. 2. 3. 4. 5. 6. 7. What percentage of nests have more than 1900 ants? What is the number of ants such that 15% of nests have more ants? What is the number of ants such that 33% of nests have fewer ants? What percentage of nests have between 700 and 1900 ants? What percentage of nests have fewer than 300 ants? What is the number of ants such that 5% of nests have more ants? The most common 80% of number of ants in a nest are between what two values? Complete first section of Handout. Normal Distributions Slide #16

From N(0, 1), what proportion …. • … are less than 1. 5? 0. 9332 1. 5 Quantitative Value Where did 0. 9332 come from? 1) Calculus – integrate the area under the curve 2) Tables of areas under the N(0, 1) curve 3) Software – in R use distrib() – see HO Normal Distributions Slide #17