Normal Distributions Applying Standard Scores 1 The Normal

Normal Distributions Applying Standard Scores 1

The “Normal” Distribution A very interesting thing occurs when we collect data and put our data into groups. 2

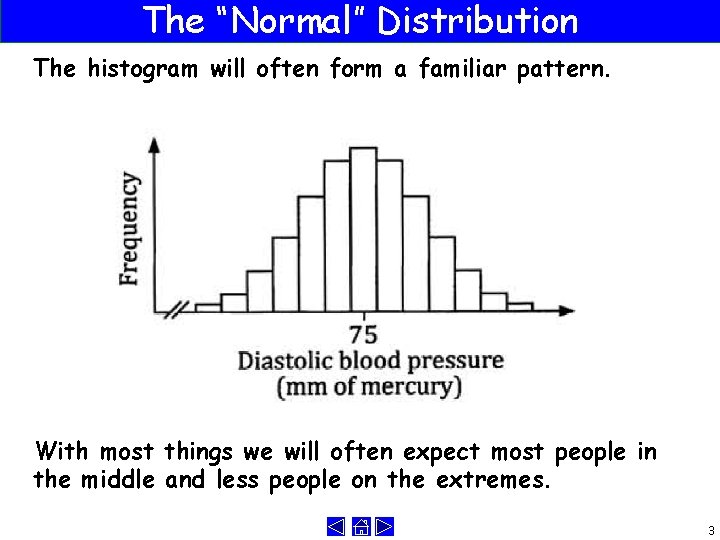
The “Normal” Distribution The histogram will often form a familiar pattern. With most things we will often expect most people in the middle and less people on the extremes. 3

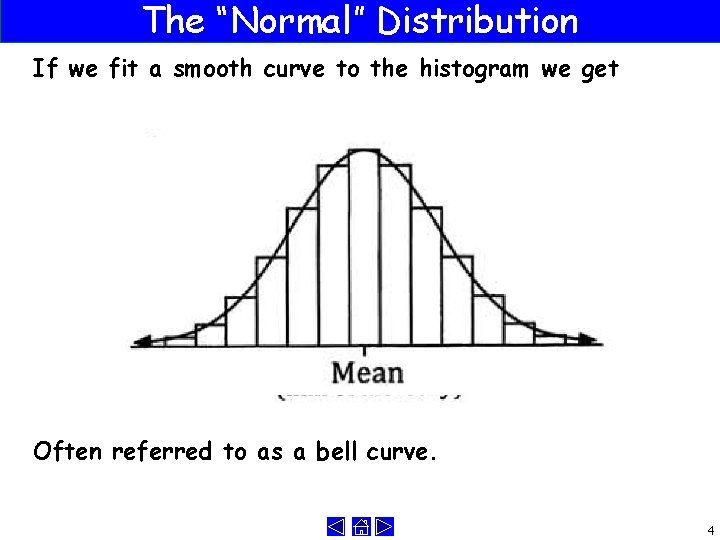
The “Normal” Distribution If we fit a smooth curve to the histogram we get Often referred to as a bell curve. 4

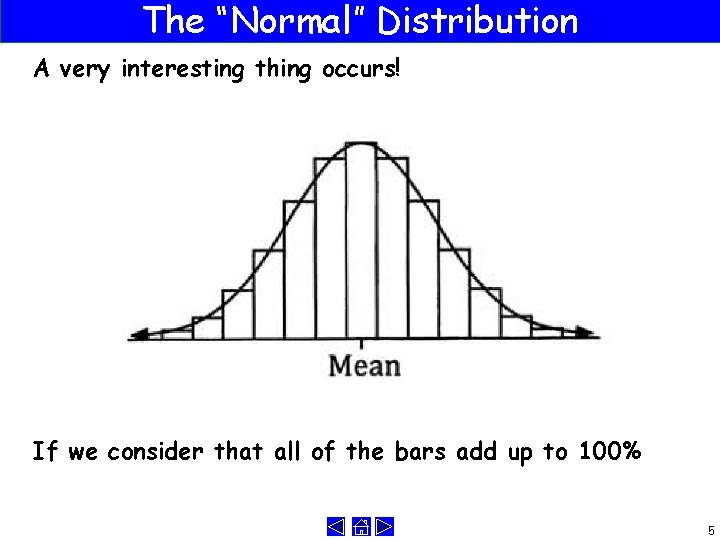
The “Normal” Distribution A very interesting thing occurs! If we consider that all of the bars add up to 100% 5

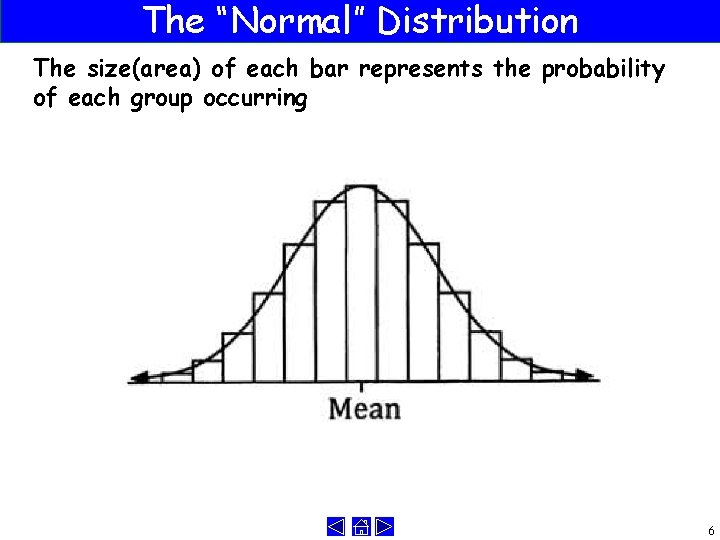
The “Normal” Distribution The size(area) of each bar represents the probability of each group occurring 6

The “Normal” Distribution Some even more amazing things are to be noticed !!! 7

The “Normal” Distribution The hump of the distribution in centred of the mean of the group. 8

The “Normal” Distribution The probability of being within a certain range (Standard deviation) of the mean often follows some simple rules. This is where standard scores start to come in. 9

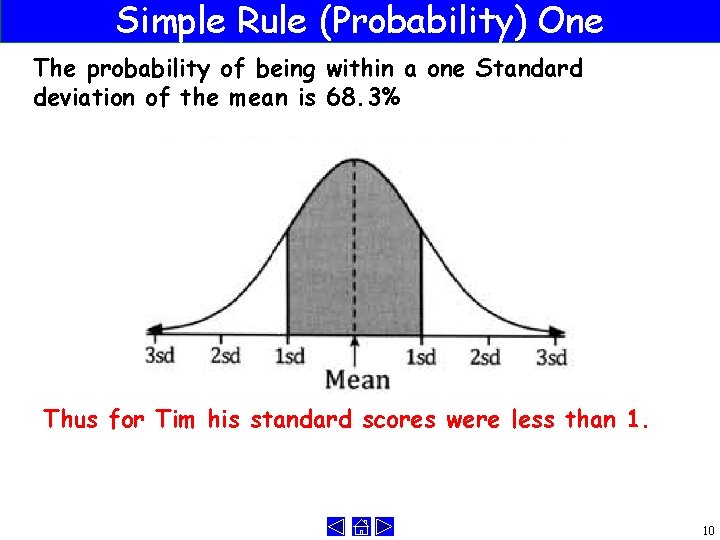
Simple Rule (Probability) One The probability of being within a one Standard deviation of the mean is 68. 3% Thus for Tim his standard scores were less than 1. 10

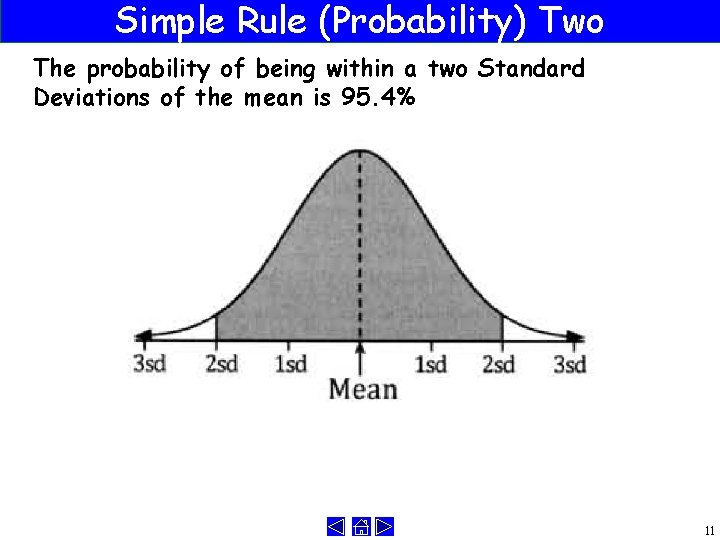
Simple Rule (Probability) Two The probability of being within a two Standard Deviations of the mean is 95. 4% 11

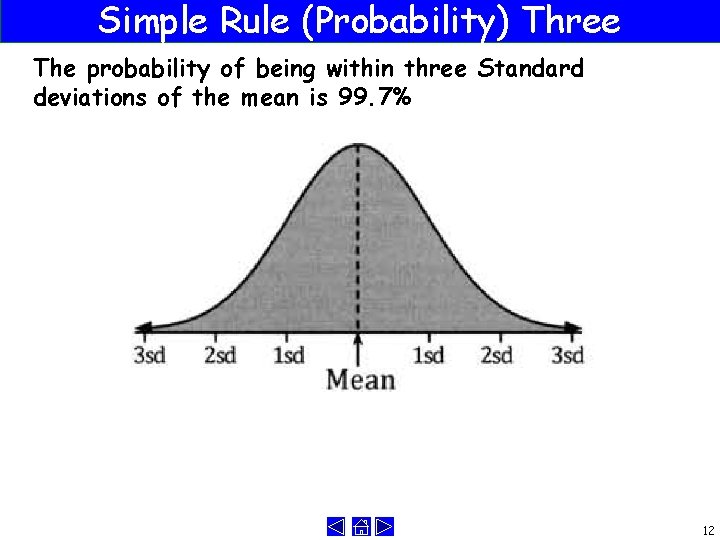
Simple Rule (Probability) Three The probability of being within three Standard deviations of the mean is 99. 7% 12

How to implement this A recent test was normally distributed. It had a mean of 50 It had a standard deviation of 5 So we might ask questions about what is the chance of me getting say between 45 and 50 13

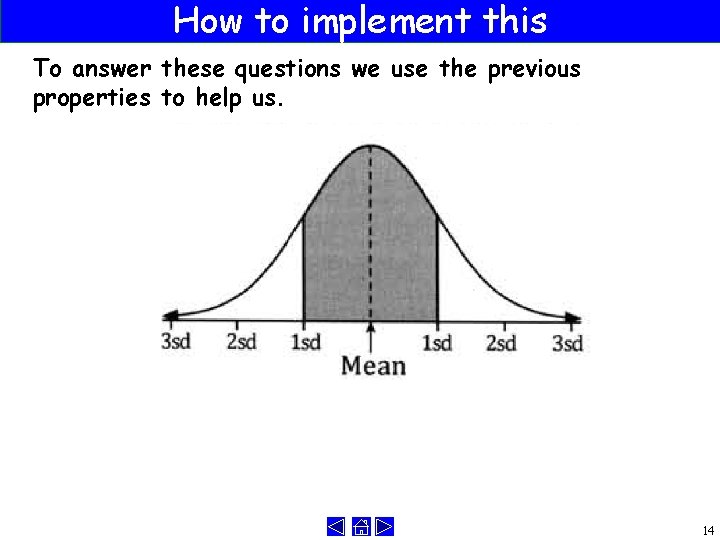
How to implement this To answer these questions we use the previous properties to help us. 14

How to implement this A recent test was normally distributed. It had a mean of 50 It had a standard deviation of 5 So we might ask questions about what is the chance of me getting say between 50 or more 15

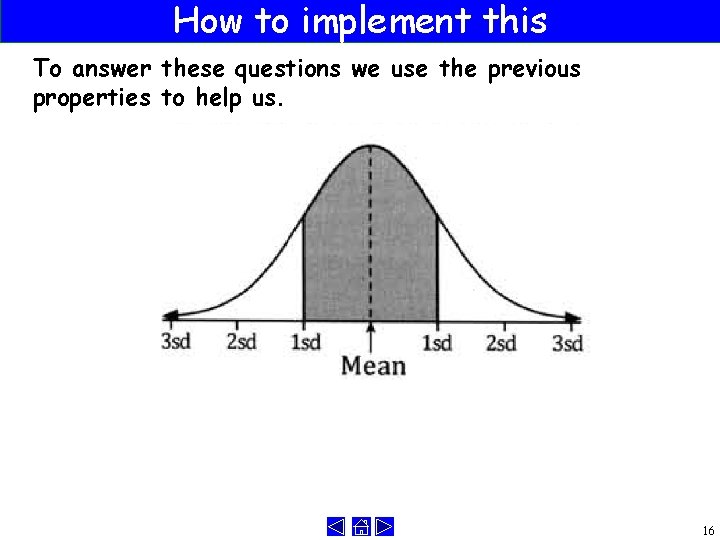
How to implement this To answer these questions we use the previous properties to help us. 16

Calculating Probabilities. Determine the probability of each of the following: (a) If a test has an average of 20 and standard deviation of 4 determine the probability of getting a score between 12 and 26 17

Calculating Probabilities. Determine the probability of each of the following: (b) If a test has an average of 0 and standard deviation of 1 determine the probability of getting a score between -1. 5 and 2 18