Normal Distribution Links The Normal Distribution Finding a

Normal Distribution Links The Normal Distribution Finding a Probability Standard Normal Distribution Inverse Normal Distribution

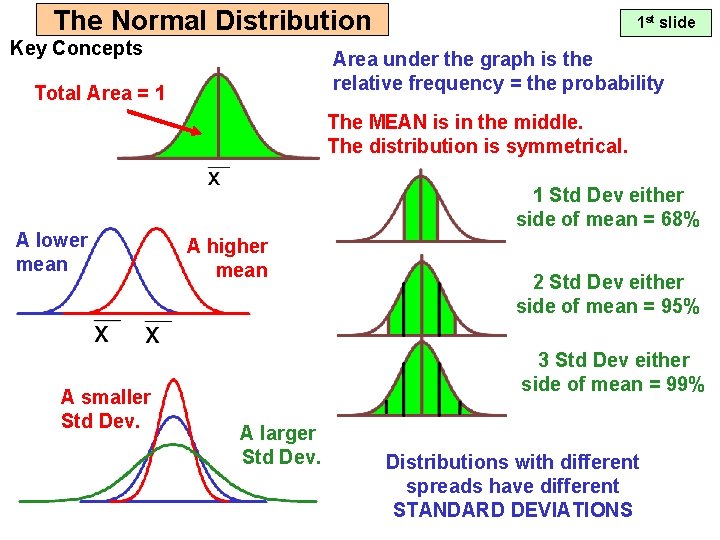
The Normal Distribution Key Concepts 1 st slide Area under the graph is the relative frequency = the probability Total Area = 1 The MEAN is in the middle. The distribution is symmetrical. A lower mean A smaller Std Dev. 1 Std Dev either side of mean = 68% A higher mean 2 Std Dev either side of mean = 95% 3 Std Dev either side of mean = 99% A larger Std Dev. Distributions with different spreads have different STANDARD DEVIATIONS

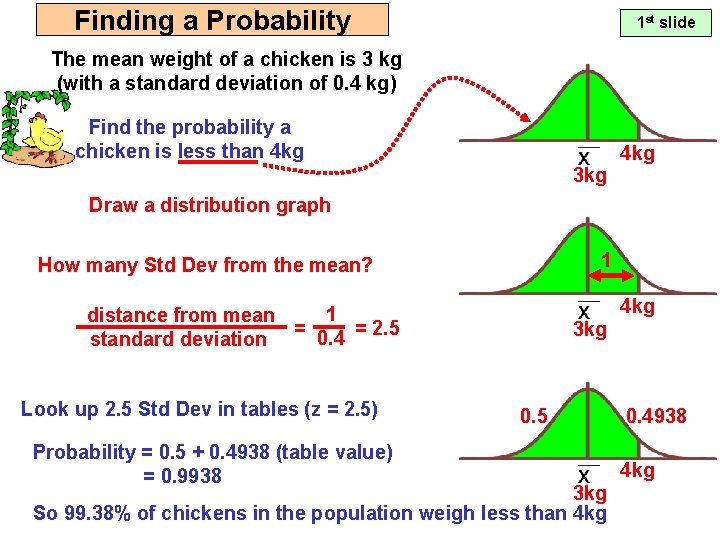
Finding a Probability 1 st slide The mean weight of a chicken is 3 kg (with a standard deviation of 0. 4 kg) Find the probability a chicken is less than 4 kg 3 kg Draw a distribution graph 1 How many Std Dev from the mean? 4 kg 1 distance from mean = = 2. 5 0. 4 standard deviation Look up 2. 5 Std Dev in tables (z = 2. 5) Probability = 0. 5 + 0. 4938 (table value) = 0. 9938 3 kg 0. 5 3 kg So 99. 38% of chickens in the population weigh less than 4 kg 0. 4938 4 kg

Standard Normal Distribution 1 st slide The mean weight of a chicken is 2. 6 kg (with a standard deviation of 0. 3 kg) Find the probability a chicken is less than 3 kg 2. 6 kg Draw a distribution graph Table value 0. 5 Change the distribution to a Standard Normal z= distance from mean 0. 4 = = 1. 333 standard deviation 0. 3 0 z = 1. 333 Aim: Correct Working The Question: P(x < 3 kg) = P(z < 1. 333) Look up z = 1. 333 Std Dev in tables Z = ‘the number of standard deviations from the mean’ = 0. 5 + 0. 4087 = 0. 9087

Inverse Normal Distribution The mean weight of a chicken is 2. 6 kg (with a standard deviation of 0. 3 kg) 1 st slide Area = 0. 9 90% of chickens weigh less than what weight? (Find ‘x’) ‘x’ kg 2. 6 kg Draw a distribution graph Look up the probability in the middle of the tables to find the closest ‘z’ value. Z = ‘the number of standard deviations from the mean’ 0. 4 0 The closest probability is 0. 3999 Look up 0. 400 Corresponding ‘z’ value is: 1. 281 z = 1. 281 The distance from the mean = ‘Z’ × Std Dev 0. 5 D = 1. 281 × 0. 3 z = 1. 281 D 2. 98 kg x = 2. 6 kg + 0. 3843 = 2. 9843 kg 2. 6 kg