NORMAL DISTRIBUTION density function Parameters mean variance 2

NORMAL DISTRIBUTION – density function Parameters: mean variance 2 1

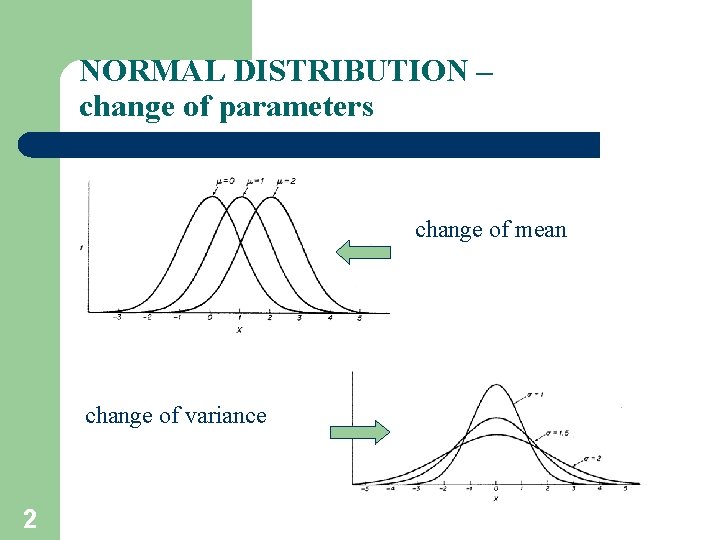
NORMAL DISTRIBUTION – change of parameters change of mean change of variance 2

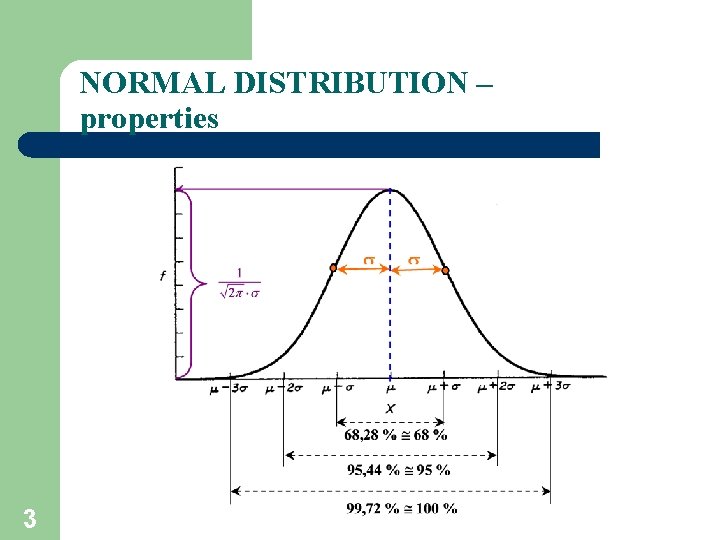
NORMAL DISTRIBUTION – properties 3

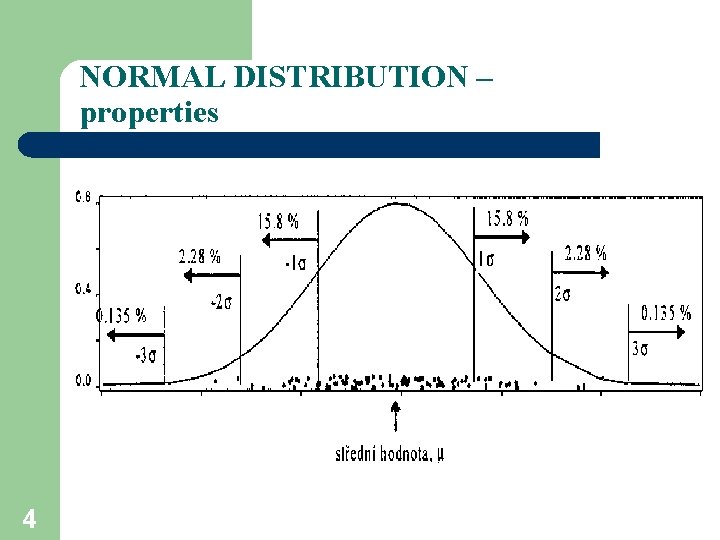
NORMAL DISTRIBUTION – properties 4

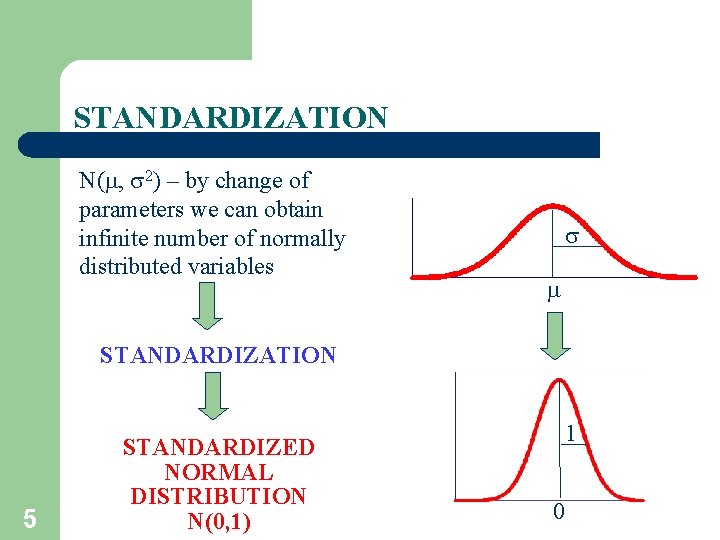
STANDARDIZATION N( , 2) – by change of parameters we can obtain infinite number of normally distributed variables STANDARDIZATION 5 STANDARDIZED NORMAL DISTRIBUTION N(0, 1) 1 0

NORMAL DISTRIBUTION– standardization Standardized normal random variable Z: 6

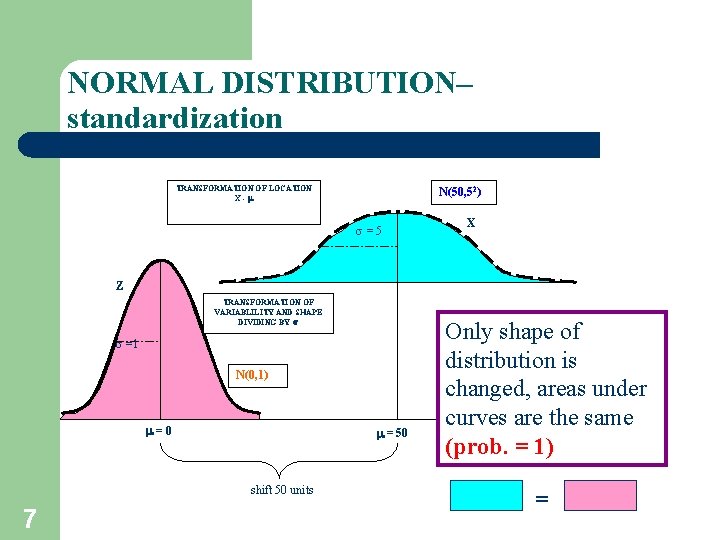
NORMAL DISTRIBUTION– standardization TRANSFORMATION OF LOCATION X- N(50, 52) =5 X Z TRANSFORMATION OF VARIABLILITY AND SHAPE DIVIDING BY =1 N(0, 1) =0 = 50 shift 50 units 7 Only shape of distribution is changed, areas under curves are the same (prob. = 1) =

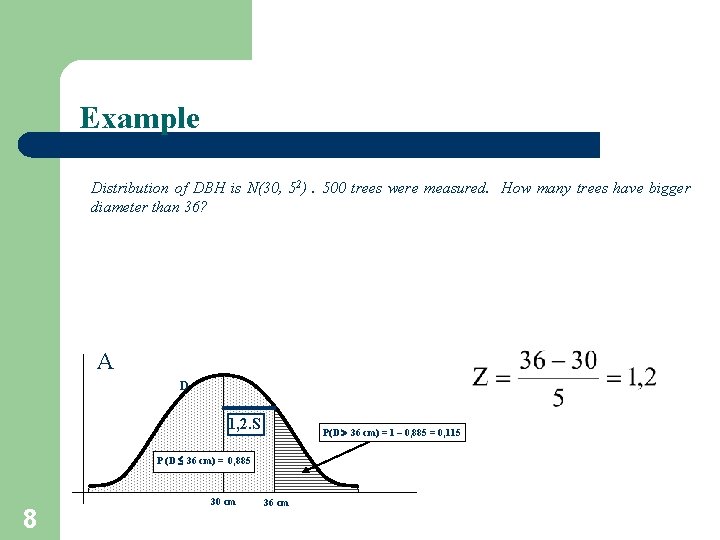
Example Distribution of DBH is N(30, 52). 500 trees were measured. How many trees have bigger diameter than 36? A D 1, 2. S P(D 36 cm) = 1 – 0, 885 = 0, 115 P (D 36 cm) = 0, 885 8 30 cm 36 cm

t-distribution (Student’s) Statistika 9 If X is a random variable with distribution N (0, 1) and Z is a random variable with distribution Chi-quadrat ( 2), T has t-distribution (Student’s) with k = n – 1 degrees of freedom

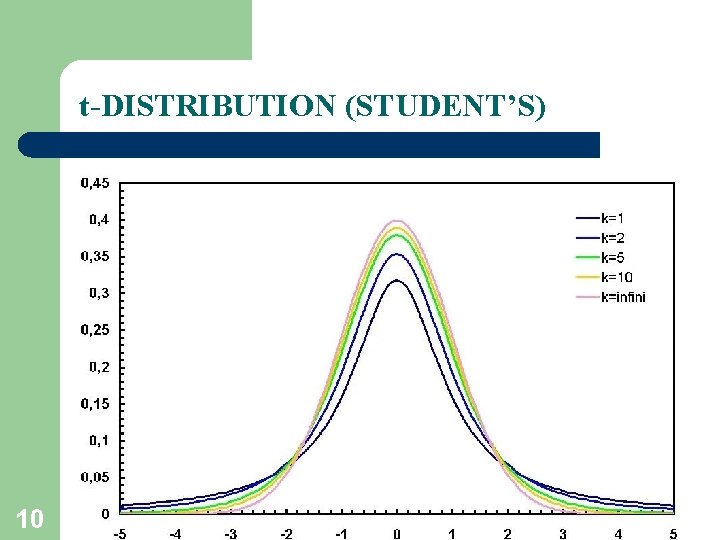
t-DISTRIBUTION (STUDENT’S) 10

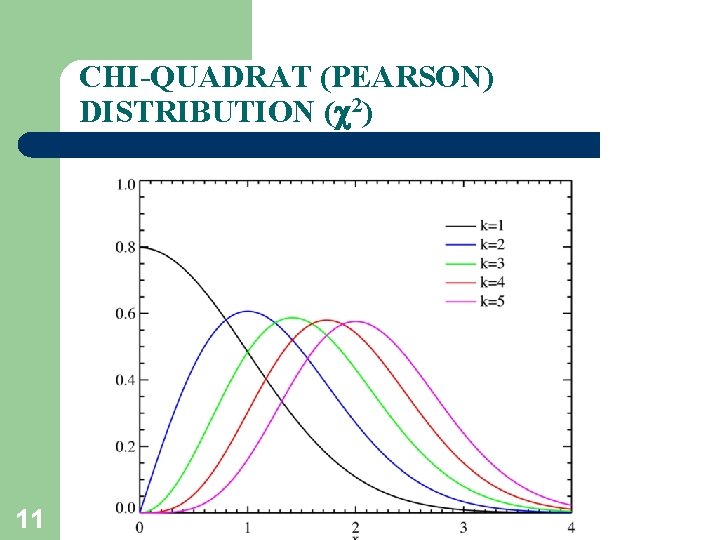
CHI-QUADRAT (PEARSON) DISTRIBUTION ( 2) 11

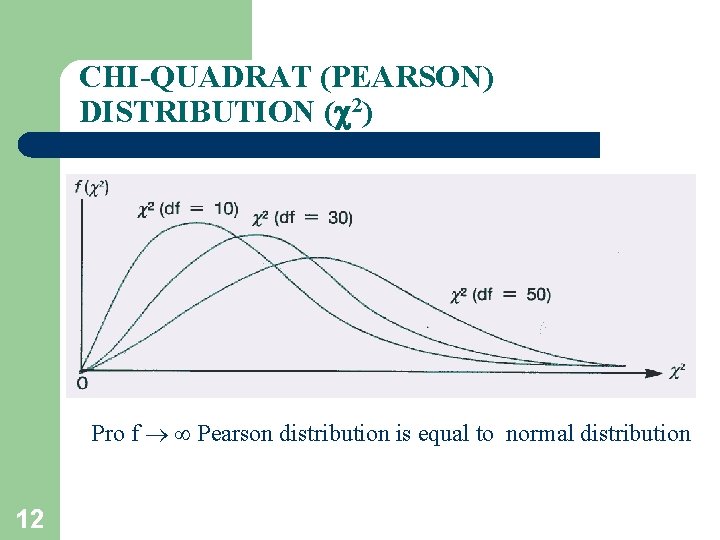
CHI-QUADRAT (PEARSON) DISTRIBUTION ( 2) Pro f Pearson distribution is equal to normal distribution 12

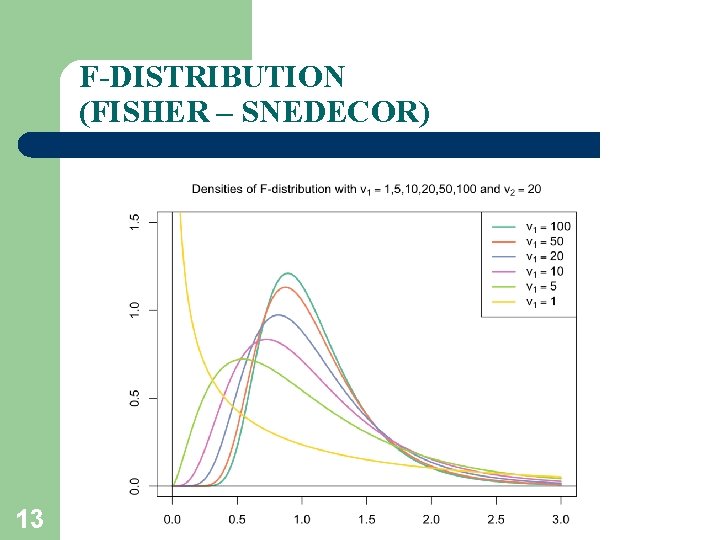
F-DISTRIBUTION (FISHER – SNEDECOR) 13

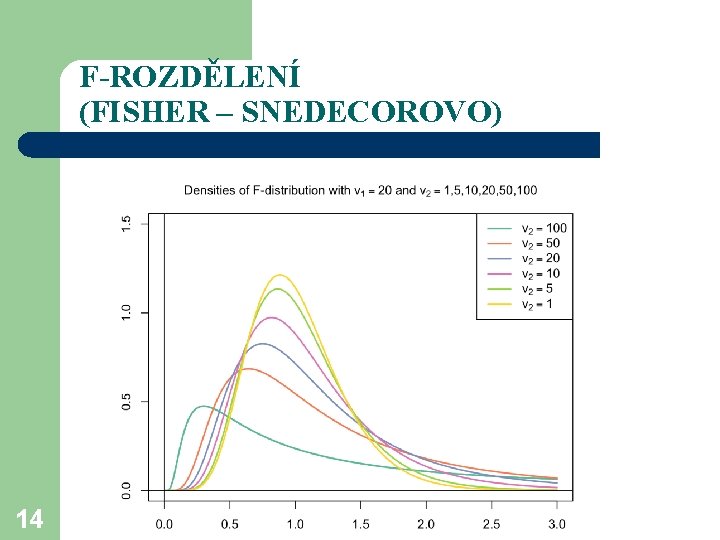
F-ROZDĚLENÍ (FISHER – SNEDECOROVO) 14