Nonstandard Normal Distributions Finding Probabilities Section 5 3

Nonstandard Normal Distributions: Finding Probabilities Section 5 -3 M A R I O F. T R I O L A Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 1

Nonstandard Normal Distributions m¹ 0 s¹ 1 z¹x v. Need to “standardize” these nonstandard distributions v. Will use z-score formula Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 2

Nonstandard Normal Distributions m¹ 0 s¹ 1 z¹x v. Need to “standardize” these nonstandard distributions v. Will use z-score formula z= x–µ s Formula 5 -2 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 3

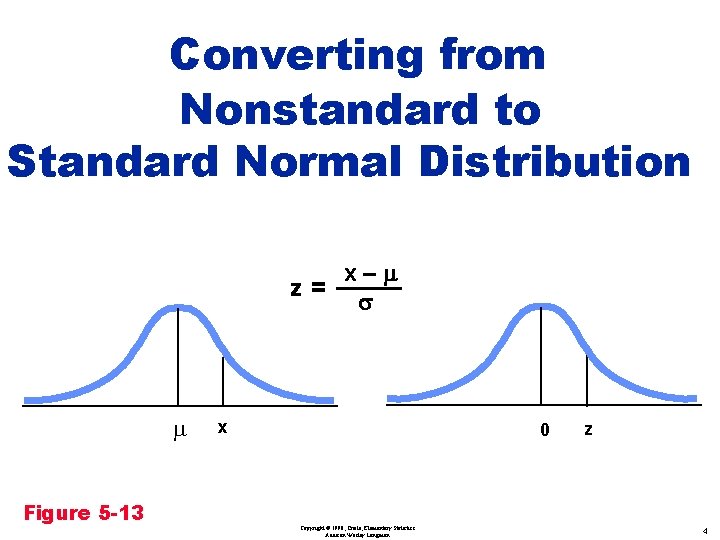
Converting from Nonstandard to Standard Normal Distribution x–m z= s m Figure 5 -13 x 0 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman z 4

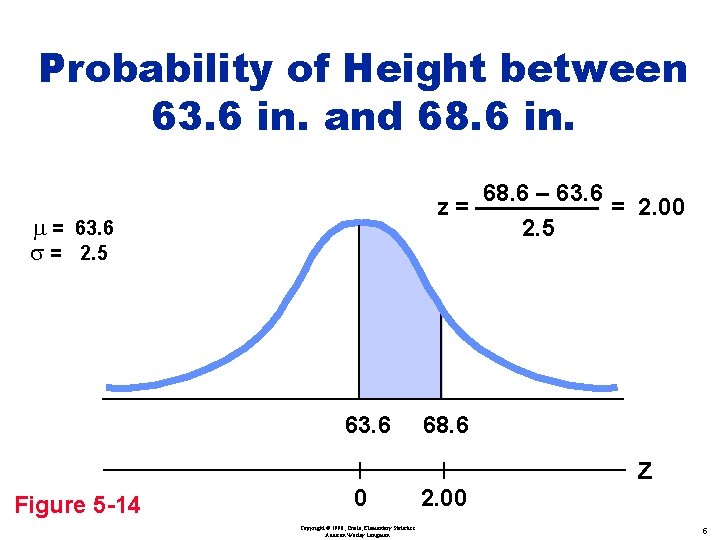
Probability of Height between 63. 6 in. and 68. 6 in. z= m = 63. 6 s = 2. 5 63. 6 Figure 5 -14 0 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 68. 6 – 63. 6 = 2. 00 2. 5 68. 6 2. 00 z 5

Nonstandard Normal Distributions: Finding Scores Section 5 -4 M A R I O F. T R I O L A Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 6

Review of 5 -2 Standard normal distribution finding z-scores when given the probability Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 7

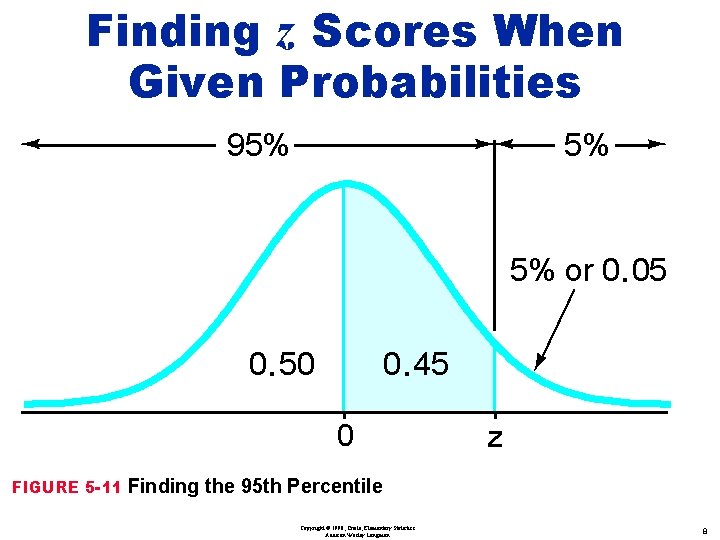
Finding z Scores When Given Probabilities 95% 5% 5% or 0. 05 0. 50 0. 45 0 FIGURE 5 -11 z Finding the 95 th Percentile Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 8

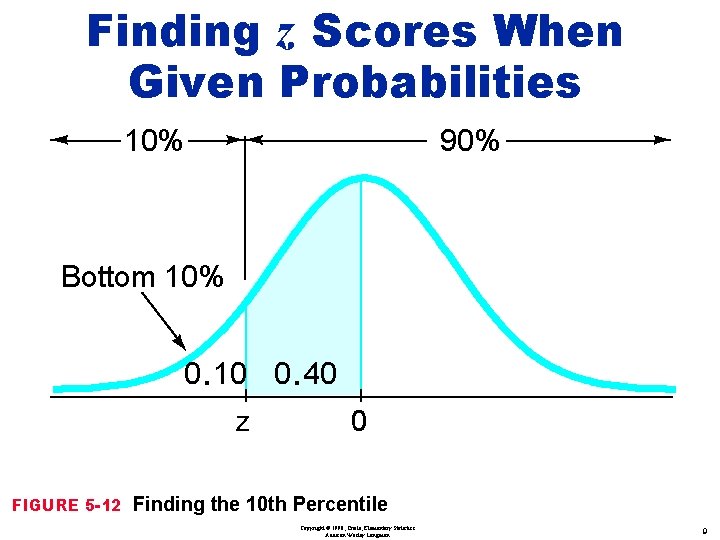
Finding z Scores When Given Probabilities 10% 90% Bottom 10% 0. 10 0. 40 z FIGURE 5 -12 0 Finding the 10 th Percentile Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 9

Finding Scores when Given Probability for Nonstandard Normal Distributions Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 10

STEPS To Find Scores When Given Probability 1. Starting with a bell curve, enter the given probability (or percentage) in the appropriate region of the graph and identify the x value(s) being sought. 2. Use Table A-2 to find the z score corresponding to the region bounded by x and the centerline of 0. Cautions: v Refer to the BODY of Table A-2 to find the closest area, then identify the corresponding z score. v Make the z score negative if it is located to the left of the centerline. 3. Using Formula 5 -2, enter the values for in step 2, then solve for x. x = µ + (z • s) µ, s, and the z score found (Another form of Formula 5 -2) 4. Refer to the sketch of the curve to verify that the solution makes sense in the context of the graph and the context of the problem. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 11

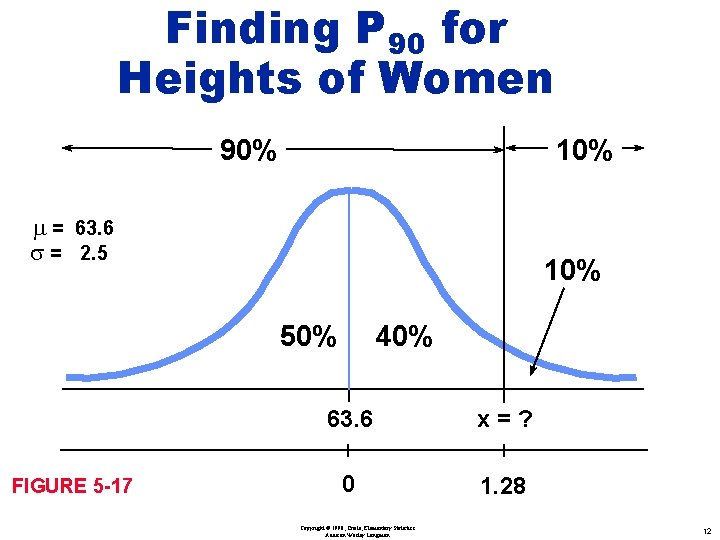
Finding P 90 for Heights of Women 90% 10% m = 63. 6 s = 2. 5 10% 50% FIGURE 5 -17 40% 63. 6 x=? 0 1. 28 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 12

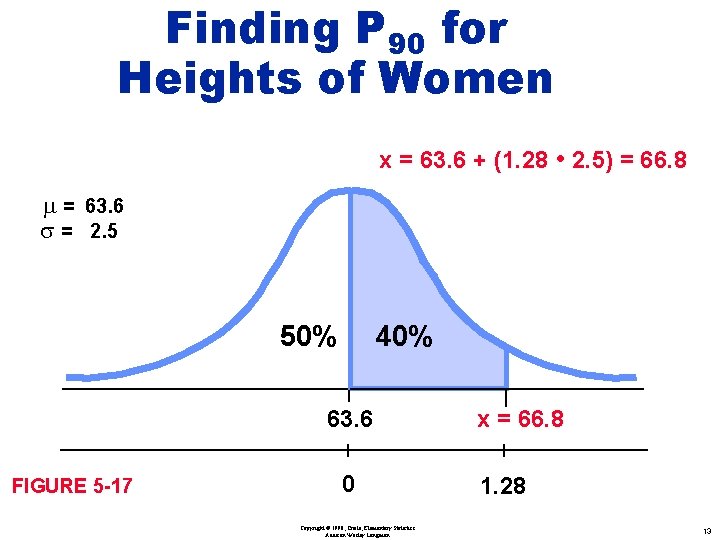
Finding P 90 for Heights of Women x = 63. 6 + (1. 28 • 2. 5) = 66. 8 m = 63. 6 s = 2. 5 50% 40% 63. 6 FIGURE 5 -17 0 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman x = 66. 8 1. 28 13

REMEMBER: z-Scores BELOW THE MEAN are NEGATIVE Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 14

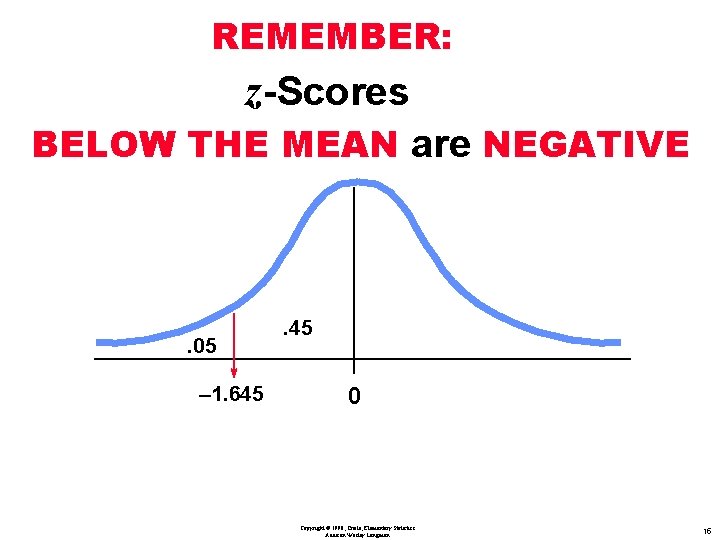
REMEMBER: z-Scores BELOW THE MEAN are NEGATIVE . 05 – 1. 645 . 45 0 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 15

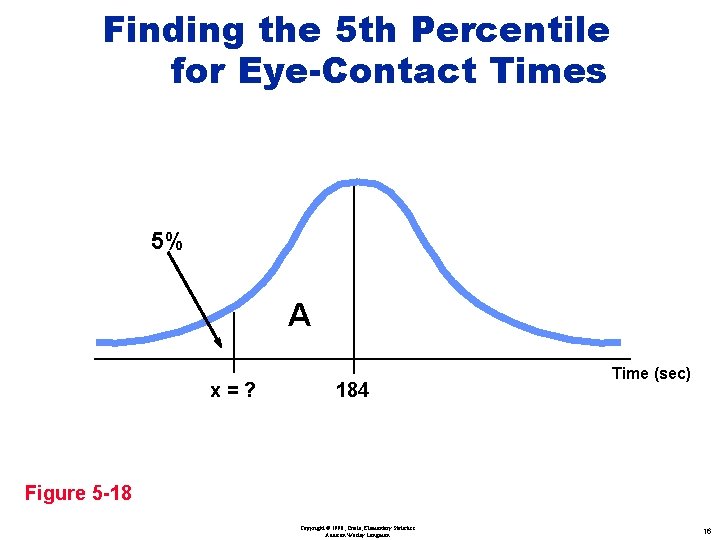
Finding the 5 th Percentile for Eye-Contact Times 5% A x=? 184 Time (sec) Figure 5 -18 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 16

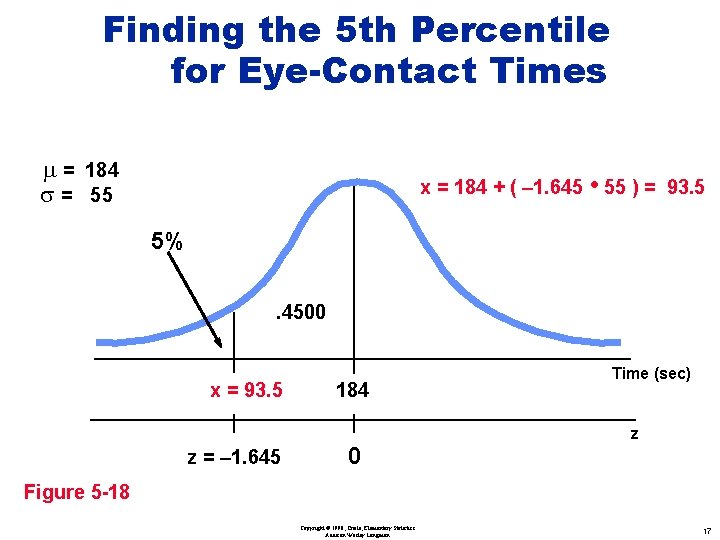
Finding the 5 th Percentile for Eye-Contact Times m = 184 s = 55 x = 184 + ( – 1. 645 • 55 ) = 93. 5 5%. 4500 x = 93. 5 z = – 1. 645 184 0 Time (sec) z Figure 5 -18 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 17