NonSemiparametric Regression and ClusteredLongitudinal Data Raymond J Carroll

Non/Semiparametric Regression and Clustered/Longitudinal Data Raymond J. Carroll Texas A&M University http: //stat. tamu. edu/~carroll@stat. tamu. edu Postdoctoral Training Program: http: //stat. tamu. edu/B 3 NC

Where am I From? Wichita Falls, my hometown I-45 Big Bend National Park I-35 College Station, home of Texas A&M 2

Acknowledgments Raymond Carroll Naisyin Wang Oliver Linton Enno Mammen Alan Welsh Xihong Lin Series of papers are on my web site Lin, Wang and Welsh: Longitudinal data Linton and Mammen: time series data 3

Outline • Longitudinal models: • panel data • Background: • splines = kernels for independent data • Nonparametric case: • do splines = kernels? • Semiparametric case: • partially linear model: • does it matter what nonparametric method is used? 4

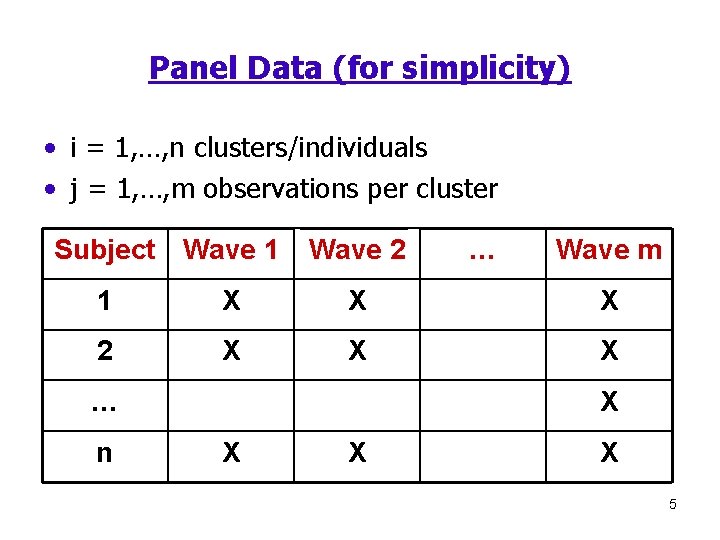
Panel Data (for simplicity) • i = 1, …, n clusters/individuals • j = 1, …, m observations per cluster Subject Wave 1 Wave 2 … Wave m 1 X X X 2 X X X … n X X 5

Panel Data (for simplicity) • i = 1, …, n clusters/individuals • j = 1, …, m observations per cluster • Important point: • The cluster size m is meant to be fixed • This is not a time series problem where the cluster size increases to infinity • We have equivalent time series results 6

The Nonparametric Model • Y = Response • X = time-varying covariate • Question : can we improve efficiency by accounting for correlation? 7

Independent Data • Two major methods • Splines (smoothing, P-splines, etc. ) with penalty parameter = l • Kernels (local averages, local linear, etc. ), with kernel function K and bandwidth h 8

Independent Data • Two major methods • Splines (smoothing, P-spline, etc. ) • Kernels (local averages, etc. ) • Both are linear in the responses • Both give similar answers in data • Silverman showed that the weight functions are asymptotically equivalent • In this sense, splines = kernels 9

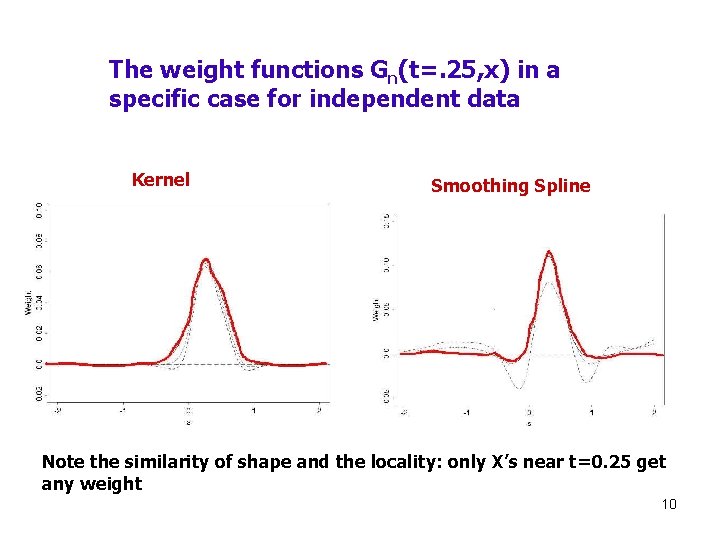
The weight functions Gn(t=. 25, x) in a specific case for independent data Kernel Smoothing Spline Note the similarity of shape and the locality: only X’s near t=0. 25 get any weight 10

Working Independence • Working independence: • Ignore all correlations • Posit some reasonable marginal variances • Splines and kernels have obvious weighted versions • Weighting important for efficiency • Splines and kernels are linear in the responses • The Silverman result still holds • In this sense, splines = kernels 11

Accounting for Correlation • Splines have an obvious analogue for nonindependent data • Let be a working covariance matrix • Penalized Generalized least squares (GLS) • Because splines are based on likelihood ideas, they generalize quickly to new problems • Kernels have no such obvious analogue 12

Accounting for Correlation • Kernels are not so obvious • Local likelihood kernel ideas are standard in independent data problems • Most attempts at kernels for correlated data have tried to use local likelihood kernel methods 13

Kernels and Correlation • Problem: how to define locality for kernels? • Goal: estimate the function at t • Let be a diagonal matrix of standard kernel weights • Standard Kernel method: GLS pretending inverse covariance matrix is • The estimate is inherently local 14

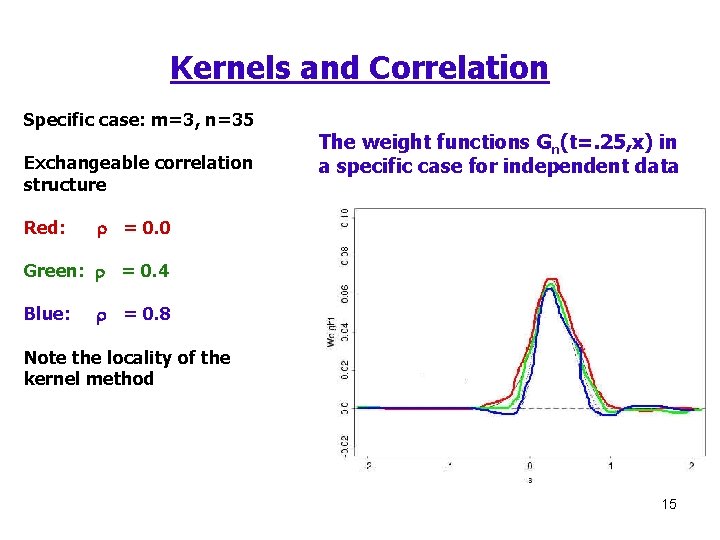
Kernels and Correlation Specific case: m=3, n=35 Exchangeable correlation structure Red: The weight functions Gn(t=. 25, x) in a specific case for independent data r = 0. 0 Green: r = 0. 4 Blue: r = 0. 8 Note the locality of the kernel method 15

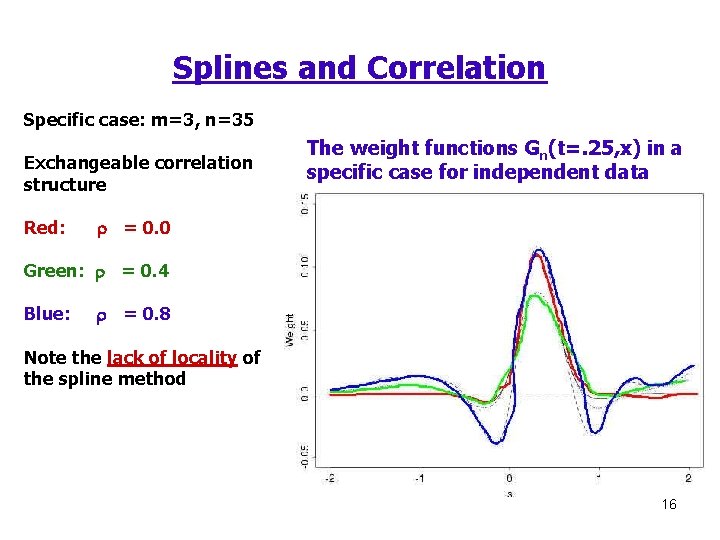
Splines and Correlation Specific case: m=3, n=35 Exchangeable correlation structure Red: The weight functions Gn(t=. 25, x) in a specific case for independent data r = 0. 0 Green: r = 0. 4 Blue: r = 0. 8 Note the lack of locality of the spline method 16

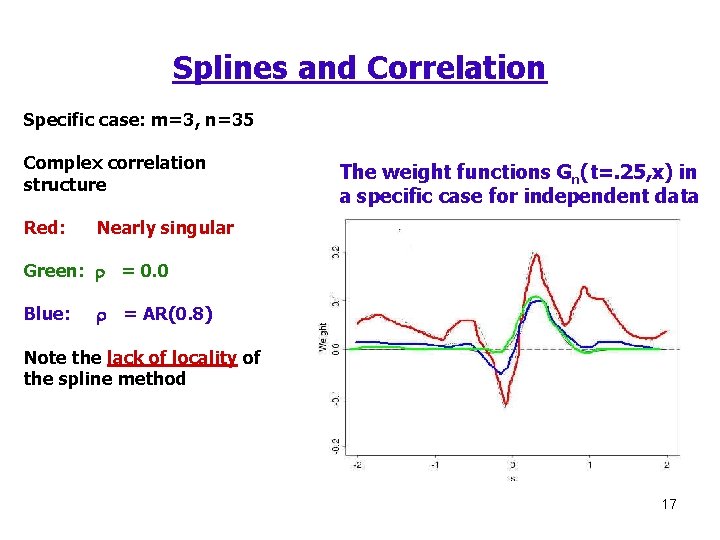
Splines and Correlation Specific case: m=3, n=35 Complex correlation structure Red: The weight functions Gn(t=. 25, x) in a specific case for independent data Nearly singular Green: r = 0. 0 Blue: r = AR(0. 8) Note the lack of locality of the spline method 17

Splines and Standard Kernels • Accounting for correlation: • Standard kernels remain local • Splines are not local • Numerical results can be confirmed theoretically • Don’t we want our nonparametric regression estimates to be local? 18

Results on Kernels and Correlation • GLS with weights • Optimal working covariance matrix is working independence! • Using the correct covariance matrix • Increases variance • Increases MSE • Splines Kernels (or at least these kernels) 19

Better Kernel Methods: SUR • Iterative, due to Naisyin Wang • Consider current state in iteration • For every j, • assume function is fixed and known for • Use the seemingly unrelated regression (SUR) idea • For j, form estimating equation for local averages/linear for jth component only using GLS with weights • Sum the estimating equations together, and solve 20

SUR Kernel Methods • It is well known that the GLS spline has an exact, analytic expression • We have shown that the SUR kernel method has an exact, analytic expression • Both methods are linear in the responses • Relatively nontrivial calculations show that Silverman’s result still holds • Splines = SUR Kernels 21

Nonlocality • The lack of locality of GLS splines and SUR kernels is surprising • Suppose we want to estimate the function at t • All observations in a cluster contribute to the fit, not just those with covariates near t • Somewhat similar to GLIM’s, there is a residualadjusted pseudo-response that • has expectation = response • Has local behavior in the pseudo-response 22

Nonlocality • Wang’s SUR kernels = pseudo kernels with a clever linear transformation. Let • SUR kernels are working independence kernels 23

The Semiparametric Model • Y = Response • X, Z = time-varying covariates • Question: can we improve efficiency for b by accounting for correlation? 24

The Semiparametric Model • General Method: Profile likelihood • Given b, solve for Q, say • Your favorite nonparametric method applied to • Working independence • Standard kernel • SUR kernel 25

Profile Methods • Given b, solve for Q, say • Then fit WI/GLS to the model with mean • Standard kernel methods have awkward, nasty properties • SUR kernel methods have nice properties • Semiparametric asymptotically efficient 26

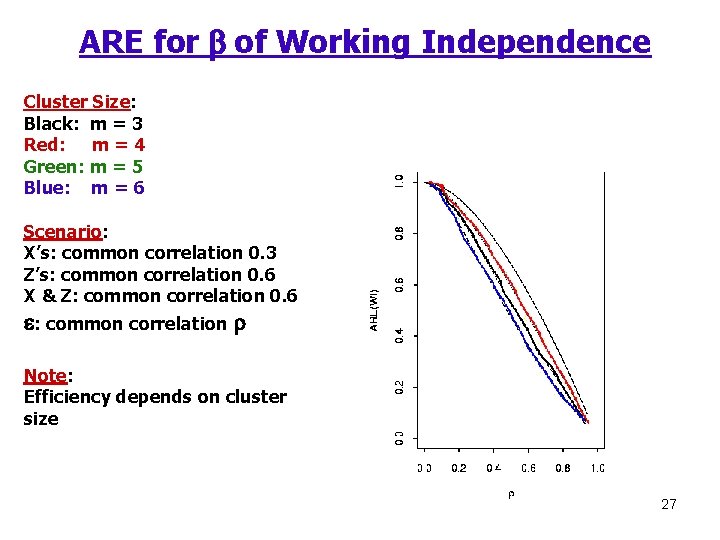
ARE for b of Working Independence Cluster Size: Black: m = 3 Red: m = 4 Green: m = 5 Blue: m = 6 Scenario: X’s: common correlation 0. 3 Z’s: common correlation 0. 6 X & Z: common correlation 0. 6 e: common correlation r Note: Efficiency depends on cluster size 27

Profile Methods • Given b, solve for Q, say • Then fit GLS to the model with mean • If you fit working independence for your estimate of Q, there is not that great a loss of efficiency 28

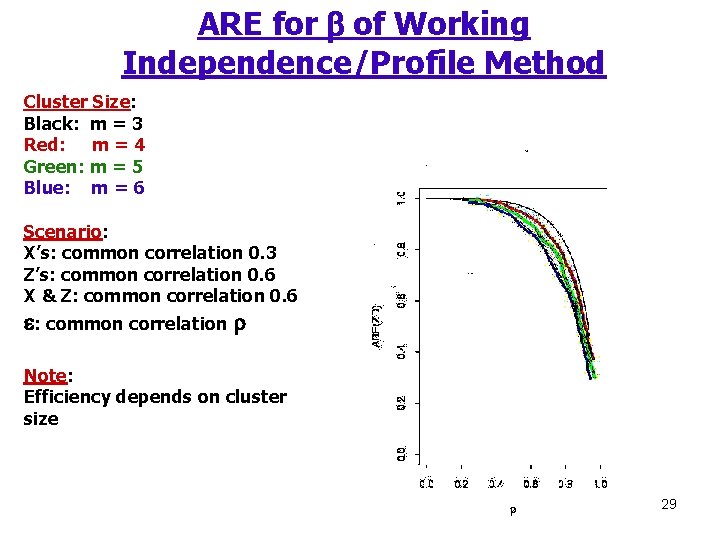
ARE for b of Working Independence/Profile Method Cluster Size: Black: m = 3 Red: m = 4 Green: m = 5 Blue: m = 6 Scenario: X’s: common correlation 0. 3 Z’s: common correlation 0. 6 X & Z: common correlation 0. 6 e: common correlation r Note: Efficiency depends on cluster size 29

Conclusions • In nonparametric regression • • Kernels = splines for working independence Working independence is inefficient Standard kernels splines for correlated data SUR kernels = splines for correlated data • In semiparametric regression • Profiling SUR kernels is efficient • Profiling: GLS for b and working independence for Q is nearly efficient 30