Nonparametric Factor Analysis with Beta Process Priors John

Nonparametric Factor Analysis with Beta Process Priors John Paisley and Lawrence Carin Department of Electrical & Computer Engineering Duke University, Durham, NC, USA

Outline n Introduction n Beta Process Review n Beta Process Factor Analysis Model (BP-FA) n Variational Inference for the BP-FA Model n Experiments n Conclusion

Introduction n Nonparametric Bayesian priors are useful for finding compact statistical representations of a data set without limiting the potential complexity of the model (e. g. , the Dirichlet process) n Factor analysis modeling is a framework where nonparametric priors can be useful. FA models are used to separate the important covariance structure of a data set from idiosyncratic noise. Inferring the value for K is something that suggests the use of a nonparametric prior. n The beta process (two-parameter) is a nonparametric prior that allows (above), while selecting a sparse subset of columns of. This process is denoted

The Beta Process • Illustration: Define H 0 to correspond to the uniform distribution Uni(0, 1)
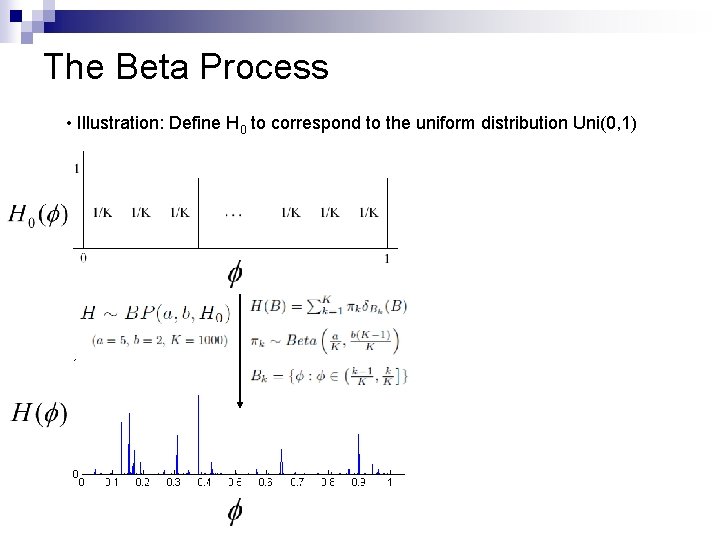
The Beta Process • Illustration: Define H 0 to correspond to the uniform distribution Uni(0, 1)
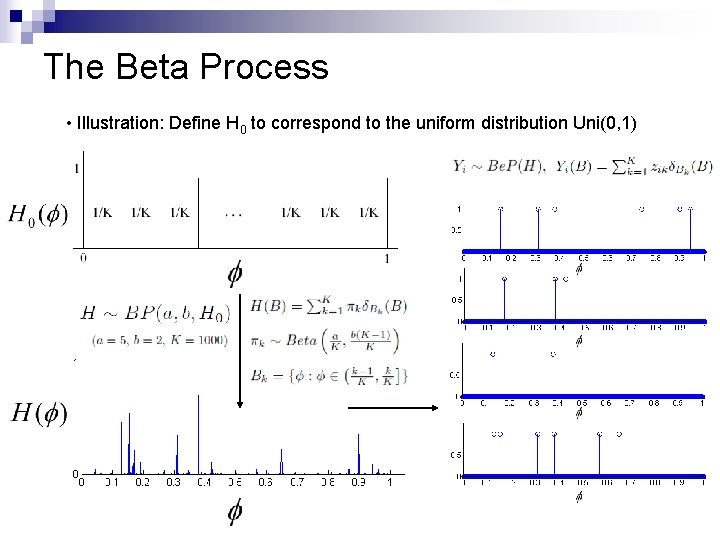
The Beta Process • Illustration: Define H 0 to correspond to the uniform distribution Uni(0, 1)

Beta Process Properties n By integrating out each to obtain the Indian buffet process (Griffiths & Ghahramani, 2005), additional properties of the beta process can be derived. n Let zi be the binary vectors on the previous slide. In the limit as n For any set of N vectors, {z 1, …, z. N}, if CN is the total number of unique locations where there is a one, then

Beta Process Factor Analysis (BP-FA) n For the factor analysis model, we model the generation of X using a finite approximation to the beta process. This approximation allows for variational inference to be performed. n Below is a noiseless, unweighted example of a draw from the model, where we show the sparseness of the BP prior using the vector of probabilities generated in the previous slides. (Only 23 of the 1000 factors are used in N = 100 samples) An illustration of the structure of the beta process prior (noiseless, unweighted model)

Beta Process Factor Analysis (BP-FA) n The generative process is at right. n This approximation can be thought of as similar to using a finite Dirichlet prior for mixture modeling. The benefit of sparseness is still present (since K is set to a large number). n The mean and covariance under this truncation is given at right. We see that the model remains well-defined as

Variational Inference for the BP-FA Model

Variational Inference for the BP-FA Model
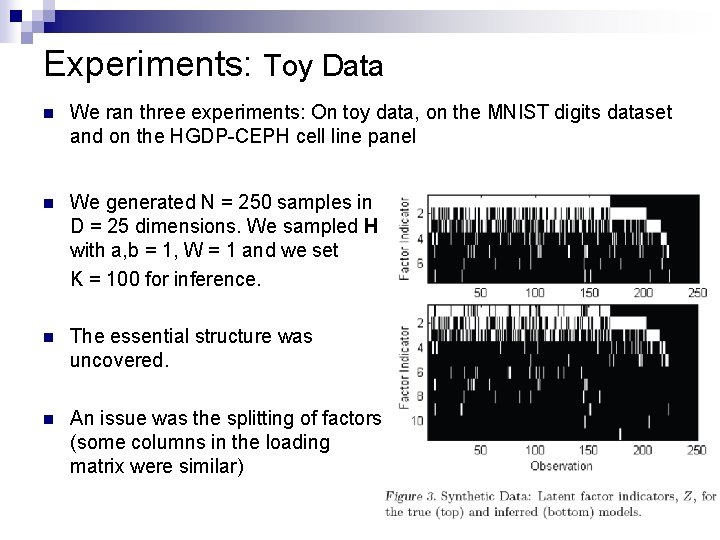
Experiments: Toy Data n We ran three experiments: On toy data, on the MNIST digits dataset and on the HGDP-CEPH cell line panel n We generated N = 250 samples in D = 25 dimensions. We sampled H with a, b = 1, W = 1 and we set K = 100 for inference. n The essential structure was uncovered. n An issue was the splitting of factors (some columns in the loading matrix were similar)
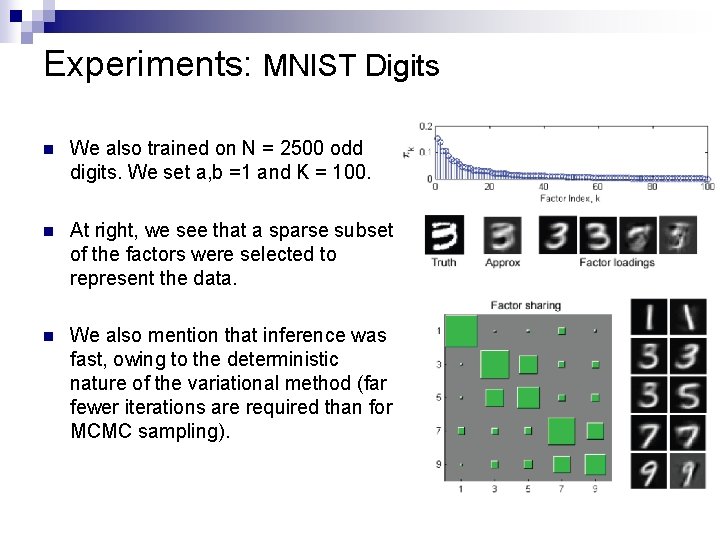
Experiments: MNIST Digits n We also trained on N = 2500 odd digits. We set a, b =1 and K = 100. n At right, we see that a sparse subset of the factors were selected to represent the data. n We also mention that inference was fast, owing to the deterministic nature of the variational method (far fewer iterations are required than for MCMC sampling).
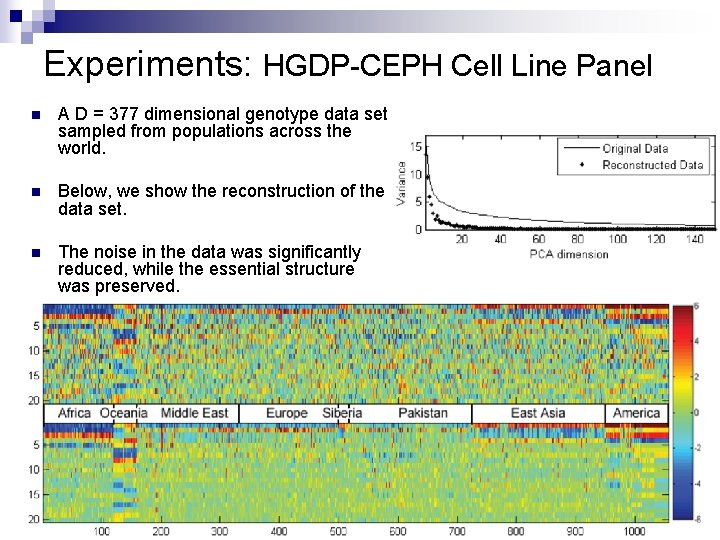
Experiments: HGDP-CEPH Cell Line Panel n A D = 377 dimensional genotype data set sampled from populations across the world. n Below, we show the reconstruction of the data set. n The noise in the data was significantly reduced, while the essential structure was preserved.

Conclusion and Future Work n We have presented a nonparametric model for performing factor analysis that uses the beta process prior. n A finite approximation to the beta process allowed for variational inference to be performed. n We are currently in the process of expanding these ideas in a fulllength paper, where we will look more in depth at applications. n A stick-breaking construction of the beta process has been recently derived by the authors. Future work is needed to rigorously prove convergence properties (help is welcome!)

References
- Slides: 16