Nonlinear Knowledge in Kernel Approximation Olvi Mangasarian Edward

Nonlinear Knowledge in Kernel Approximation Olvi Mangasarian Edward Wild University of Wisconsin-Madison

Objectives v Primary objective: Incorporate prior knowledge over completely arbitrary sets in function approximation without kernelizing the knowledge v Secondary objective: Achieve transparency of the prior knowledge for practical applications

Outline v Use kernels for function approximation v Incorporate prior knowledge Ø Previous approaches: require transformation of knowledge Ø New approach does not require any transformation of knowledge • Knowledge given over completely arbitrary sets v Experimental results Ø Two synthetic examples and one real world example related to breast cancer prognosis Ø Approximations with prior knowledge more accurate than approximations without prior knowledge

Function Approximation v Given a set m of points in n-dimensional real space Rn and corresponding function values in R Ø Points are represented by rows of a matrix A Rm n Ø Exact or approximate function values for each point are given by a corresponding vector y Rm v Find a function f: Rn R based on the given data Ø f(Ai 0) yi

Function Approximation v. Problem: utilizing only given data may result in a poor approximation ØPoints may be noisy ØSampling may be costly v. Solution: use prior knowledge to improve the approximation

Adding Prior Knowledge v. Standard approach: fit function at given data points without knowledge v. Constrained approach: satisfy inequalities at given points v. MSW 2004: satisfy linear inequalities over polyhedral regions v. Proposed approach: satisfy nonlinear inequalities over arbitrary regions

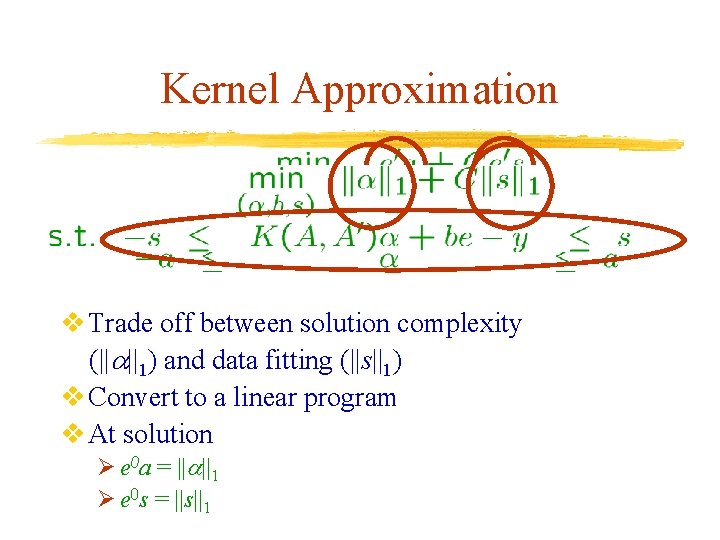
Kernel Approximation v. Approximate f by a nonlinear kernel function K Øf(x) K(x 0, A 0) + b m 0 0 2) ØK(x , A ) = exp( ||x-A || i i i=1 v. Error in kernel approximation of given data Ø-s K(A, A 0) + be - y s Øe is a vector of ones in Rm

Kernel Approximation v Trade off between solution complexity (|| ||1) and data fitting (||s||1) v Convert to a linear program v At solution Ø e 0 a = || ||1 Ø e 0 s = ||s||1

Incorporating Nonlinear Prior Knowledge (MSW 2004) v Bx d 0 Ax+ b h 0 x + v Need to “kernelize” knowledge from input space to feature space of kernel v Requires change of variable x = A 0 t v BA 0 t d 0 AA 0 t + b h 0 A 0 t + v K(B, A 0)t d 0 K(A, A 0)t + b h 0 A 0 t + v Motzkin’s theorem of the alternative gives an equivalent linear system of inequalities which is added to a linear program v Achieves good numerical results, but kernelization is not readily interpretable in the original space

Incorporating Nonlinear Prior Knowledge: New Approach v Start with arbitrary nonlinear knowledge implication v g(x) 0 K(x 0, A 0) + b h(x), 8 x 2 v g, h are arbitrary functions v g: ½ Rn ! Rk, h: ! R v Problem: need to add this knowledge to the optimization problem v Logically equivalent system: v g(x) 0, K(x 0, A 0) + b - h(x) < 0 has no solution x

Prior Knowledge as a System of Linear Inequalities v Use a theorem of the alternative for convex functions: Assume g(x), K(x 0, A 0) + b, -h(x) are convex functions of x, and that is convex. Then Ø I. g(x) 0, K(x 0, A 0) + b - h(x) < 0 has a solution x , or Ø II. v Rk, v 0: K(x 0, A 0) + b - h(x) + v 0 g(x) 0 x Ø But never both. v If we can find v 0: K(x 0, A 0) + b - h(x) + v 0 g(x) 0 x , then by above theorem Ø g(x) 0, K(x 0, A 0) + b - h(x) < 0 has no solution x or equivalently: Ø g(x) 0 K(x 0, A 0) + b h(x), 8 x 2

Proof v I II Ø Mangasarian 1969, Corollary 4. 2. 2 v I II Ø Suppose not. That is, there exists x 2 , v 2 Rk, , v¸ 0: Ø g(x) 0, K(x 0, A 0) + b - h(x) < 0, Ø K(x 0, A 0) + b - h(x) + v 0 g(x) 0 8 x 2 Ø Then we have the contradiction: Ø 0 > K(x 0, A 0) + b - h(x) + v 0 g(x) 0 Ø Requires no assumptions on g, h, K, or whatsoever

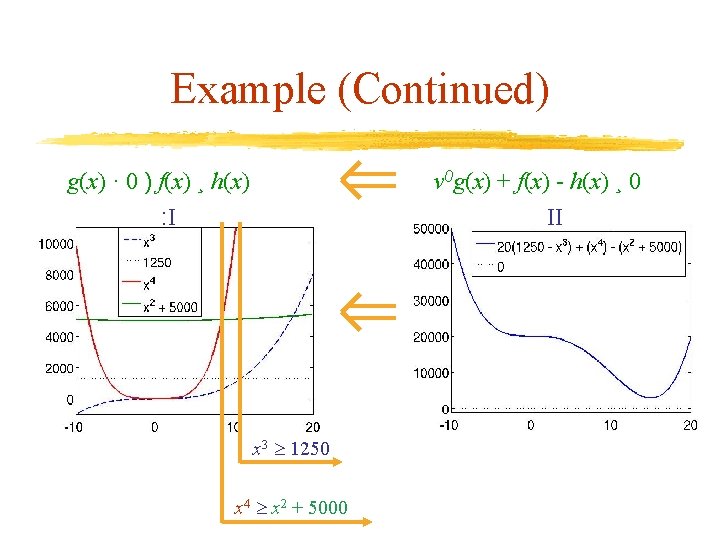
Example v Either Ø I. g(x) 0, f(x) - h(x) < 0 has a solution x , or Ø II. v Rk, v 0: v 0 g(x) + f(x)- h(x) 0 x . Ø But never both v Under no assumptions, I( II v Example Ø g(x) = 1250 - x 3 Ø f(x) = x 4 Ø h(x) = x 2 + 5000 Ø = [-10, 20]

Example (Continued) v. II: Ø v 0 g(x) + f(x)- h(x) 0 x 2 Ø 20(1250 - x 3) + (x 4) - (x 2 + 5000) 0 x 2 [-10, 20] v. II Implies : I: Øg(x) 0, f(x) - h(x) < 0 has no solution x 2 Ø 1250 - x 3 0, (x 4) - (x 2 + 5000) < 0 has no solution [-10, 20] ØEquivalently: x 3 1250 x 4 x 2 + 5000 x

Example (Continued) g(x) · 0 ) f(x) ¸ h(x) : I v 0 g(x) + f(x) - h(x) ¸ 0 II x 3 1250 x 4 x 2 + 5000

Incorporating Prior Knowledge v Linear semi-infinite program: infinite number of constraints v Discretize: finite linear program Ø Slacks allow knowledge to be satisfied inexactly Ø Add term to objective function to drive slacks to zero

Numerical Experience v Evaluate on three datasets Ø Two synthetic datasets Ø Wisconsin Prognostic Breast Cancer Database v Compare approximation with prior knowledge to one without prior knowledge Ø Prior knowledge leads to an improved approximation Ø Prior knowledge used cannot be handled exactly by previous work Ø No kernelization needed on knowledge set

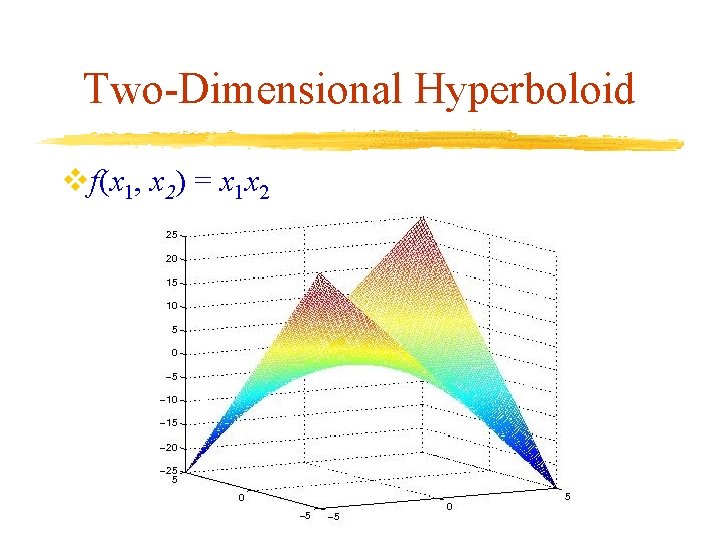
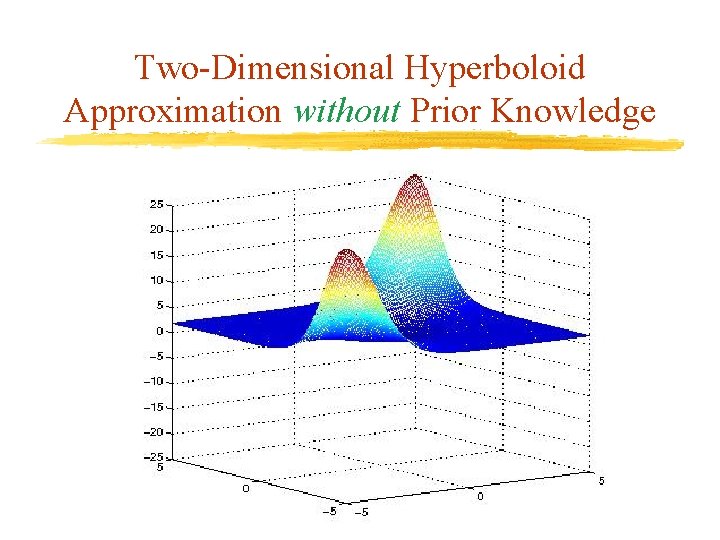
Two-Dimensional Hyperboloid vf(x 1, x 2) = x 1 x 2

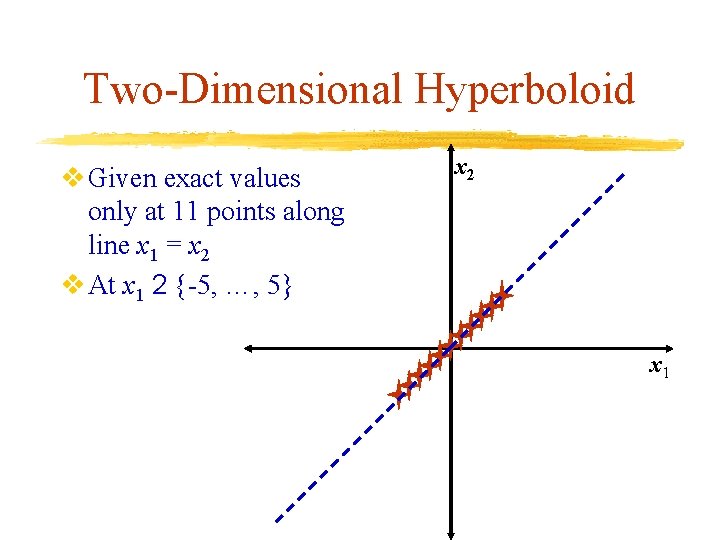
Two-Dimensional Hyperboloid v Given exact values only at 11 points along line x 1 = x 2 v At x 1 2 {-5, …, 5} x 2 x 1

Two-Dimensional Hyperboloid Approximation without Prior Knowledge

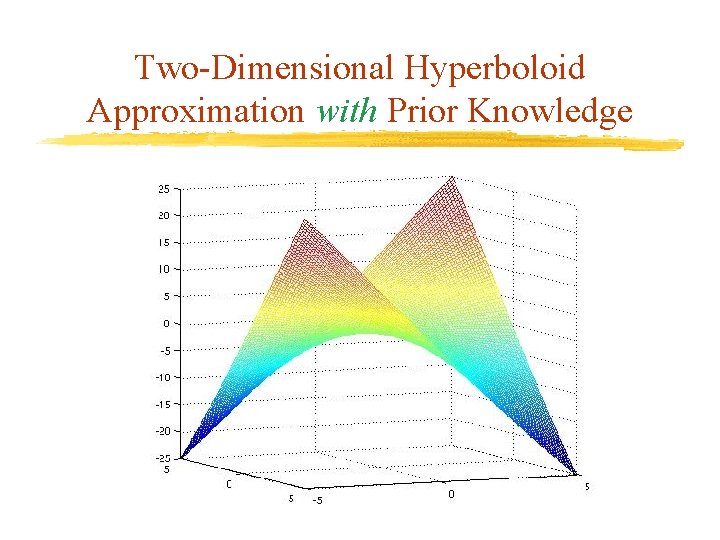
Two-Dimensional Hyperboloid v. Add prior knowledge: Øx 1 x 2 1 f(x 1, x 2) x 1 x 2 v. Nonlinear term x 1 x 2 can not be handled exactly by any previous approach v. Discretization gives points along the line x 1 = -x 2, x 1 {-5, -4, …, 4, 5}

Two-Dimensional Hyperboloid Approximation with Prior Knowledge

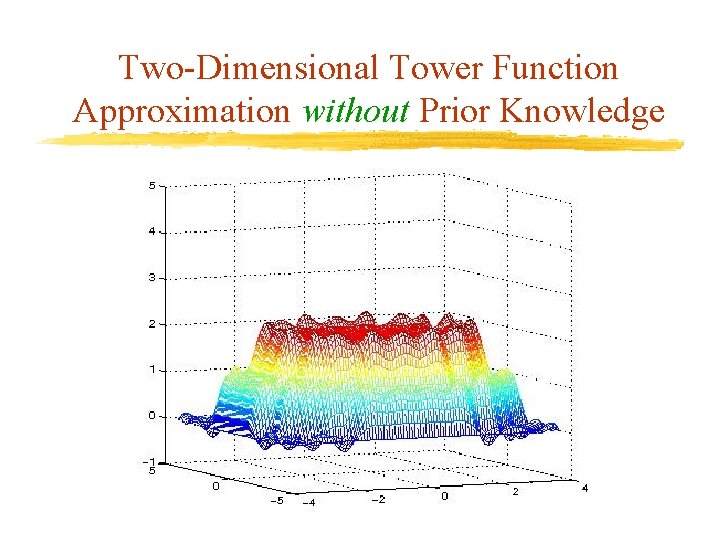
Two-Dimensional Tower Function

Two-Dimensional Tower Function Data v. Given 400 points on the grid [-4, 4] v. Values are min{g(x), 2}, where g(x) is the exact tower function

Two-Dimensional Tower Function Approximation without Prior Knowledge

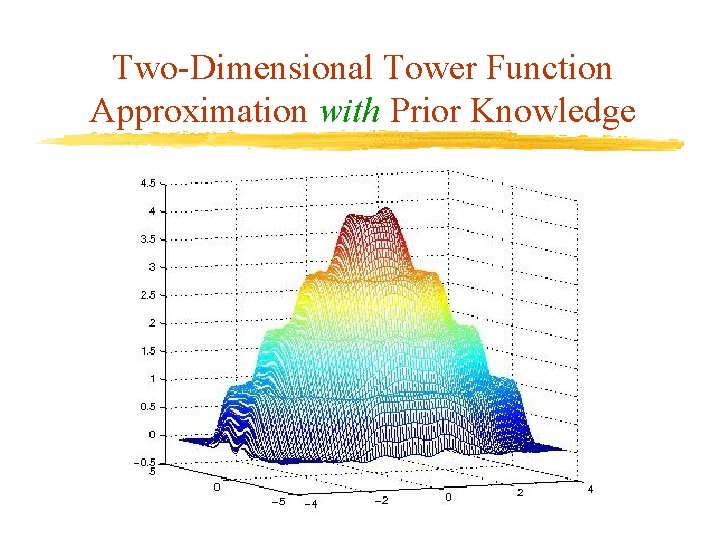
Two-Dimensional Tower Function Prior Knowledge v. Add prior knowledge: Ø(x 1, x 2) [-4, 4] f(x) = g(x) v. Prior knowledge is the exact function value. v. Enforced at 2500 points on the grid [4, 4] [-4, 4] v. Prior knowledge can be used to give a good approximation despite poor data

Two-Dimensional Tower Function Approximation with Prior Knowledge

Predicting Lymph Node Metastasis v Number of metastasized lymph nodes is an important prognostic indicator for breast cancer recurrence v Determined by surgery in addition to the removal of the tumor v Wisconsin Prognostic Breast Cancer (WPBC) data Ø Lymph node metastasis for 194 patients Ø 30 cytological features from a fine-needle aspirate Ø Tumor size, obtained during surgery v Task: predict the number of metastasized lymph nodes given tumor size

Predicting Lymph Node Metastasis v. Split data into two portions ØPast data: 20% used to find prior knowledge ØPresent data: 80% used to evaluate performance v. Simulates acquiring prior knowledge from an expert’s experience

Prior Knowledge for Lymph Node Metastasis v Use kernel approximation without knowledge on the past data Ø f 1(x) = K(x 0, A 10) 1 + b 1 Ø A 1 is the matrix of the past data points v Use density estimation to decide where to enforce knowledge Ø p(x) is the empirical density of the past data v Number of metastasized lymph nodes is greater than the predicted value on the past data, with tolerance of 0. 01 Ø p(x) 0. 1 f(x) f 1(x) - 0. 01

Predicting Lymph Node Metastasis: Results Approximation f 1(x) from past data Without knowledge With knowledge RMSE 6. 12 5. 92 5. 04 v Table shows root-mean-squared-error (RMSE) of approximations on present data Ø Average error reported for f 1(x) Ø Leave-one-out error reported for approximations with and without knowledge v Improvement due to knowledge: 14. 8%

Conclusion v Added general nonlinear prior knowledge to kernel approximation Ø Implemented as linear inequalities in a linear programming problem Ø Knowledge incorporated transparently v Demonstrated effectiveness Ø Two synthetic examples Ø Real world problem from breast cancer prognosis v Future work Ø More general prior knowledge with inequalities replaced by more general functions Ø Apply to classification problems

Questions v. Websites linking to papers and talks: vhttp: //www. cs. wisc. edu/~olvi/ vhttp: //www. cs. wisc. edu/~wildt/