NONLINEAR FUZZY CONTROL FUZZY PID CONTRL And TAKAGISUGENOKANG

NON-LINEAR FUZZY CONTROL, FUZZY PID CONTRL, And TAKAGI-SUGENO-KANG (TSK or TS) FUZZY CONTROL A Presentation / Talk By Dr. J. S. Saini Prof. , EED; Dean, Faculty of Engg. & Tech. , D. C. R. Univ. of Sci. & Tech. , Murthal, Sonipat Ph. : 9416351300, 9416354914, Email: jssain@rediffmail. com References: (1) J. S. Saini, Editor, “Proc. of AICTE-ISTE STTP on ‘Fuzzy Control: From Analytical Foundations to Applications in Chaos in Fuzzy Logic Controllers’, at CRSCE, Murthal, 1 Sonipat w. e. f. 2. 8. 04 to 14. 8. 04. (2) J. S. Saini, “Lecture Notes

• INTRODUCTION • Euphoria: fuzzy ctrl found as essentially a nonlinear map. • Myth Exploded: pioneering works Mac Vicar-Whelan[137], Tang et. al. [135], Ying[134: 1987]: some FLCs shown linear PI ctrlers. Fuzzy ctrler to multilevel relay ctrl[14: 1978]. Euphoria waned: [111, 133, 136, 138 -140]. • Questions: • Anything special about FLCs that makes them behave so well? • Do FLCs work well because their structures are peculiar? • What are their structures then? • How true are some claims? • Some publications claim FLCs more robust than conventional ones (linear PIDs etc. ) 2 • Such claims supported by ltd. computer simulation only & w/o

• Are these claims real? How can the claims be validated? • How to design FLCs with as little trial-and-error effort as possible? • Inherent Difficulties in Analytical Study of FLCs: Despite d fnal interpretability, structural obscurity of FLCs: difficult to make out, precisely, analytically & objectively, causes (nonlinearity & var gains) of superior perf of FLCs with certain operators (t-norms, s-norms), mfs, sfs, etc. • Worse Yet: No clear relationships b/n these parameters & ctrler performance. • A Curse in Disguise: Avoiding separate modeling task, ctrl probs. solved more tly, effectively thro’ fuzzy ctrl. Practice stand pt: fuzzy techniques , cost effective, greater ease of application popularity. • Harder to analyze mathematically: black-box sys’s. 3

• The Curse of Dimensionality: FLC usually has far more design parameters than comparable conventional controller, industrially dominant PID has only 3. • Primary Difficulty: Tech prob. for conventional ctrl: find ctrller structure & parameters on basis of given sys model. • Pri. difficulty in FLCs: analytical structure unavailable even after FLC constructed. W/o unveiling analytical str. of FLCs, design: trial-&-error /rules of thumb: art, rather than in the spirit of conventional ctrl design. • Sharing A Common Flaw: Existing fuzzy sys development s/w packages share common flaw: lack of analytical capabilities: Inability to derive analytical structure of FLC, let alone mathematically design a sys, determine its stability/any other 4 sys properties.

Ø Bottom Line: • Necessary: resulting structure be sensible in context of conventional ctrl theory. • Merely deriving analytical structure: not enough; must be represented in a closed form clearly understandable from ctrl theory stand-pt. • Only such a structure gives essential platform on which well-developed conventional ctrl & sys theory, linear/ nonlinear, can be used to analytically analyze & design FLCs. 5

ØMAIN THRUST: • Distinction b/n Linear & Nonlinear Fuzzy Controllers • Ways to introduce non-linearity in fuzzy rules • How overlapping of mfs spreads non-linearity to different regions? • Distinction b/n Fuzzy Controller of PID Type & Fuzzy PID Controller • Linearity or Non-linearity of each element & of overall FLC • TAKAGI-SUGENO-KANG (TSK) or TAKAGI-SUGENO (TS) FUZZY SYSTEMS • DISTINCTIONS BETWEEN TAKAGI-SUGENO (TS) & MAMDANI FUZZY SYSTEMS 6

v LINEAR & NONLINEAR FUZZY CONTROLLERS • A fuzzy ctrler is linear (or nonlinear) if its defuzzified o/p: linear (or nonlinear) fn of its i/ps. • A general fuzzy rule with two i/p vars & one o/p var : IF E(n) is A˜i & R(n) is B˜j THEN u(n) is V˜k where k = f(i, j) & V˜k is a fuzzy set. • If f(i, j) is a linear fn. , fuzzy rule is called a linear fuzzy rule. • Whether or not a fuzzy rule is linear depends on the fn. relating the indices of i/p fuzzy sets to that of o/p fuzzy set. • If V˜k is a singleton fuzzy set, a gen linear fuzzy rule written as: IF E(n) is A˜i & R(n) is B˜j THEN u(n) is Vk (17) where Vk = ai + bj + c (18) NOTE: above =n does not represent a Takagi-Sugeno (TS) rule consequent as i & j are ‘indices’ and that e(n) & r(n) are not 7 involved.

(19) & the linear rule becomes: IF E(n) is A˜i & R(n) is B˜j THEN u(n) is (i + j)V (20) NOTE: For linear fuzzy rule, distance b/n two adjacent singleton o/p fuzzy sets is: Vk+1 – Vk = (i + j +1)V – (i + j)V = V for all k, where V = a const design parameter chosen by ctrl designer. So, o/p fuzzy sets for a linear fuzzy rule are equally spaced; space is V. • However, for a nonlinear fuzzy rule, o/p fuzzy sets may not be all equally spaced & Vk will be related to i & j (indices of antecedent fuzzy sets) thro’ a nonlinear fn instead of (18). • If whole rule base is constructed from linear rules, ctrl table shall be symmetric about one diagonal & anti-symmetric 8 about the other. However, a nonlinear ctrl table shall be non-

(such indexing paves way for mathematical analysis of fuzzy ctrl): • {A˜-2, A˜-1, A˜ 0, A˜ 1, A˜ 2, etc. } symbolize -ve Medium (NM), -ve Small (NS), Zero (ZO), +ve Small (PS) & +ve Medium (PM). • If these five are identical (say) i/p fuzzy sets for E(n) & similar ones (say, B˜-2, B˜-1, B˜ 0, B˜ 1, B˜ 2} for R(n), • Then according to (20), there would be nine o/p fuzzy sets {V˜V˜-1, V˜ 0, V˜ 1, V˜ 2, V˜ 3, V˜ 4} which may be 4, V˜-3, V˜-2, interpreted as {-ve Very Large (NVL), -ve Large (NL), -ve Medium (NM), -ve Small (NS), Zero (ZO), +ve Small (PS), PM, PL, PVL}. • Then linear & nonlinear ctrl rules are shown in Tables (1) & (2): Table 1 25 Linear Rules according to (17) when k = i + j Table 2 25 Nonlinear Rules with respect to Linear ones in 9 Table 1

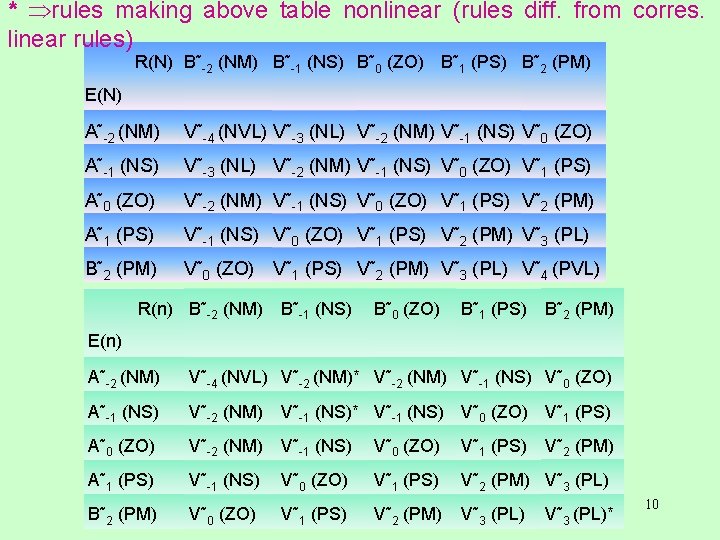
* rules making above table nonlinear (rules diff. from corres. linear rules) R(N) B˜-2 (NM) B˜-1 (NS) B˜ 0 (ZO) B˜ 1 (PS) B˜ 2 (PM) E(N) A˜-2 (NM) V˜-4 (NVL) V˜-3 (NL) V˜-2 (NM) V˜-1 (NS) V˜ 0 (ZO) A˜-1 (NS) V˜-3 (NL) V˜-2 (NM) V˜-1 (NS) V˜ 0 (ZO) V˜ 1 (PS) A˜ 0 (ZO) V˜-2 (NM) V˜-1 (NS) V˜ 0 (ZO) V˜ 1 (PS) V˜ 2 (PM) A˜ 1 (PS) V˜-1 (NS) V˜ 0 (ZO) V˜ 1 (PS) V˜ 2 (PM) V˜ 3 (PL) B˜ 2 (PM) V˜ 0 (ZO) V˜ 1 (PS) V˜ 2 (PM) V˜ 3 (PL) V˜ 4 (PVL) R(n) B˜-2 (NM) B˜-1 (NS) B˜ 0 (ZO) B˜ 1 (PS) B˜ 2 (PM) E(n) A˜-2 (NM) V˜-4 (NVL) V˜-2 (NM)* V˜-2 (NM) V˜-1 (NS) V˜ 0 (ZO) A˜-1 (NS) V˜-2 (NM) V˜-1 (NS)* V˜-1 (NS) V˜ 0 (ZO) V˜ 1 (PS) A˜ 0 (ZO) V˜-2 (NM) V˜-1 (NS) V˜ 0 (ZO) V˜ 1 (PS) A˜ 1 (PS) V˜-1 (NS) V˜ 0 (ZO) V˜ 1 (PS) V˜ 2 (PM) V˜ 3 (PL) B˜ 2 (PM) V˜ 0 (ZO) V˜ 1 (PS) V˜ 2 (PM) V˜ 3 (PL)* 10

rules: • fuzzy ctrl table is made asymmetrical about either diagonal or both diagonals. • Another equivalent but with less locality of ctrl than above: assign asymmetrical values to o/p singletons (to distribute o/p fuzzy sets asymmetrically over o/p UOD) e. g. if o/p UOD is [-100, 100], then taking {-100, -80, 40, -30, 0, 25, 50, 75, 100} values for {NVL, NM, NS, ZO, PS, PM, PL, PVL} instead of {-100, -75, -50, -25, 0, 25, 50, 75, 100}. 11

12

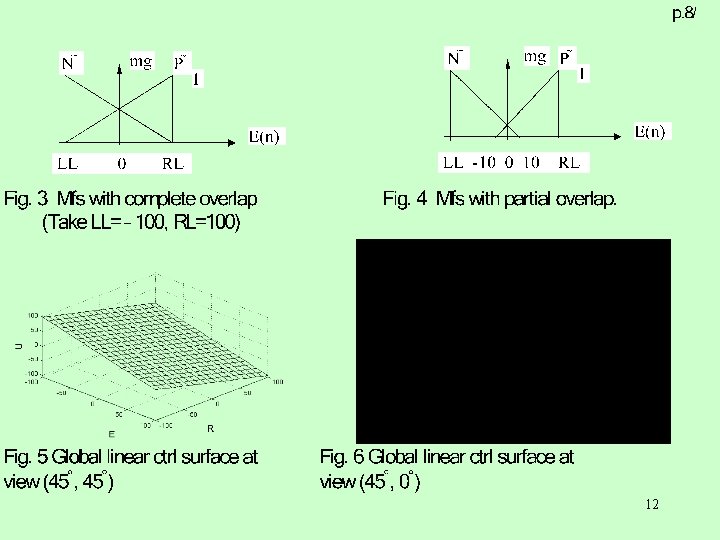
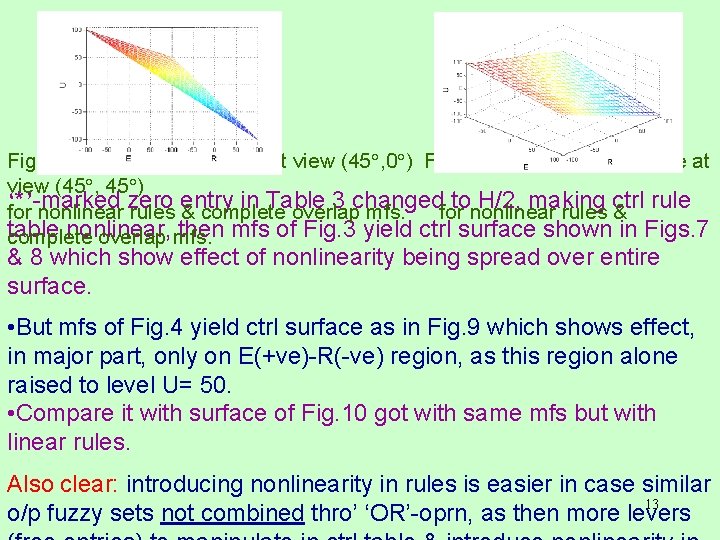
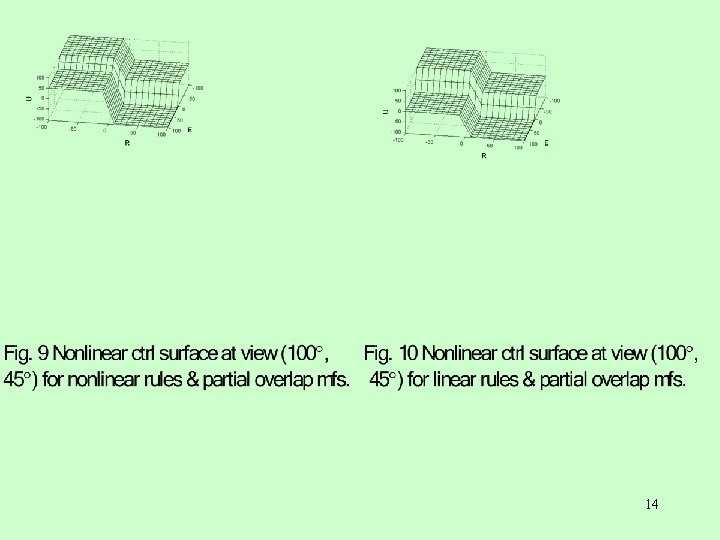
Fig. 7 Nonlinear ctrl surface at view (45 , 0 ) Fig. 8 Nonlinear ctrl surface at view (45 , 45 ) ‘*’-marked zero entry in Table 3 changedfor tononlinear H/2, making ctrl rule for nonlinear rules & complete overlap mfs. rules & table nonlinear, then mfs of Fig. 3 yield ctrl surface shown in Figs. 7 complete overlap mfs. & 8 which show effect of nonlinearity being spread over entire surface. • But mfs of Fig. 4 yield ctrl surface as in Fig. 9 which shows effect, in major part, only on E(+ve)-R(-ve) region, as this region alone raised to level U= 50. • Compare it with surface of Fig. 10 got with same mfs but with linear rules. Also clear: introducing nonlinearity in rules is easier in case similar 13 o/p fuzzy sets not combined thro’ ‘OR’-oprn, as then more levers

14

v. FUZZY PID CONTROL Ø Incorrect to call any FLC that uses same i/p vars. as conventional PID does, a Fuzzy PID Ctlr. , many found wrongly classified, after their analytical structures derived & examined. Ø FLC defined as ‘Fuzzy Controller of PID Type’ if expressible as: U(n) (or ∆U(n)) = C 0 + C 1 x 1(n) +. . . + CM x. M(n) (1) Where Ci, 0≤ i ≤ M, are either const. or variable gains changing with time (or with e(n), r(n), etc. ) & where xi(n) are i/p vars. ØFUZZY PID Control: a special case of Fuzzy Control of PID Type with C 0 = 0 & M = 3, i. e. , with 3 i/p/ vars, these 3 vars. at the rule level need be same as in conventional PID, but imp. is that ctrl. action must be expressible in form: Ø ∆U(n) = Kp r(n) + Ki e(n) + Kd d(n) (2) 15

v. FUZZY PID CONTROL contd. Ø Linear PID: 3 parameters Kp , Ki & Kd constants Non-linear PID: Atleast one of these 3 parameters varies with time and / or with e(n), r(n), or d(n). Ø Positional Form: Rule consequents specify U(n) Suitable for actuators requiring Total Control Action ØIncremental Form: Rules consequents specify ∆U(n) Suitable for actuators requiring only Change in Control Action (Store in them the impact of previous control actions exerted) 16

v. NON-LINEARITY OF FUZZY CONTROLLER Ø Linearity Superposition (Additivity & Homogeneity) Ø Additivity Property: y 1 = f(x 1) & y 2 = f(x 2) Then it y 1 + y 2 = f(x 1 + x 2) x i. e. , f(x 1 + x 2) = f(x 1) + f(x 2) System f(x) y ØScaling or Homogeneity: y = f(x) Then it . y = f(. x) i. e. , f(. x) = . f(x) ØDue to fuzzification & defuzzification, FLC = crisp T. E. ØLet the only control rule be: If x is LX then u is LU where LX and LU are linguistic values of process state ‘x’ & control output variable, ‘u’ ØMeaning of Linguistic Values given by mfs: LX : X [0, 1] and U [0, 1] var. 17

v. NON-LINEARITY OF FLC contd. ü Input Variable Scaling Or Normalization: Ø Additivity satisfied: y 1 = Nx. x 1 & y 2 = Nx. x 2 Then it y 1 + y 2 = Nx. (x 1 + x 2) i. e. , Nx. (x 1 + x 2) = Nx. x 1 + Nx. X 2 Ø Scaling satisfied: . Nx. x 1 = Nx. ( . x 1) üOutput Var. Scaling or Denormalization: ØLinear on similar grounds ü Fuzzification: ØMembership fn. µLX of the linguistic value LX is a non-linear fn. Linearity requires µLX (x 1) + µLX (x 2) = µLX(x 1+ x 2) Which cannot be fulfilled bcoz of non-linear characteristics of 18 µLX.

v. NON-LINEARITY OF FLC contd. ü Rule Firing: Linearity requires that if • u: µ′CLU (u) = µLX(x 1) Λ µLU(u) • u: µ″CLU (u) = µLX(x 2) Λ µLU(u) • then u: µ′CLU (u) + µ″CLU(u) = µLX(x 1 + x 2) Λ µLU(u) Not true for FLC as • µLU is a non-linear fn. • µ’CLU & µ’’CLU are non-linear fns. • Oprn. ‘Λ’ is non-linear for Λ= min b c a UOD 19

v. NON-LINEARITY OF FLC contd. Ø Defuzzification: • Assume Centre-of-Area Defuzzification & let u 1 & u 2 be defuzzification results, i. e. , • u 1 = ; u 2 = • Linearity requires u 1 + u 2= Instead we have u 1 + u 2 = Non-linear block. 20

v. CONCLUSION Ø FKBC is a Non-linear transfer element whose sources of non-linearity are: • Non-linearity of membership fns. • Rule firing • Defuzzification Ø Other elements such as I/p & O/p Scaling Blocks are linear elements.

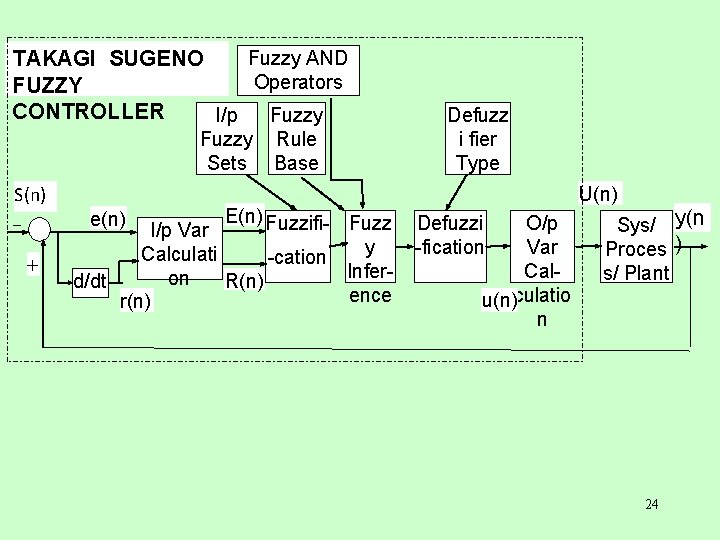
v. TAKAGI-SUGENO-KANG (TSK) or TAKAGI-SUGENO (TS) FUZZY SYSTEMS v. Functional Fuzzy Sys (FFS): TS Fuzzy Sys is a special case. For FFS: Singleton Fuzzification used & i-th MISO rule has the form: IF u 1 is & u 2 is &. . . un is THEN bi is gi(. ) Distinction: Premises are same. Whereas consequent in Mamdani Fuzzy System is a Fuzzy Set, V˜k , (giving a linguistic interpretation), yet in TSK, the bi is not o/p mf centre, but a function ØOften argument of gi contains terms ui but other variables may be used, e. g. , bi = gi (∙) = ai, 0 + ai, 1 (u 1)2 + …+ ai, n (un)2 Ø bi = gi (∙) = exp[ai, 1 Sin(u 1) + …+ ai, n Sin(un)] ØAny Fn. Can be used, e. g. , even an NN or another Fuzzy Sys. 22

MAMDANI FUZZY CTRLLER I/p Sfs Fuzzy Logic Operators I/p Fuzzy Rule Sets Base S(n) e(n) + d/dt I/p Var Scaling r(n) E(n) Fuzzifi-cation R(n) Fuzzy Defuzz Inference i fier Method Type O/p Sfs U(n) Fuzz y Inference Defuzzi -fication O/p Var Scaling u(n) Sys/ y(n Proces ) s/ Plant 23

Fuzzy AND TAKAGI SUGENO Operators FUZZY CONTROLLER I/p Fuzzy Sets S(n) E(n) Fuzzifi- Fuzz I/p Var y Calculati -cation Inferon d/dt R(n) ence r(n) e(n) + Rule Base Defuzz i fier Type U(n) Defuzzi -fication O/p Var Calu(n)culatio n Sys/ y(n Proces ) s/ Plant 24

v. DISTINCTIONS BETWEEN TAKAGI-SUGENO (TS) & MAMDANI FUZZY SYSTEMS 1. TS FCs don’t use sfs for i/p & o/p vars. Scaling implicitly done by TS rule structure: each i/p var. multiplied by a coeff. in consequent of every fuzzy rule. Coeff. not specifically used for scaling but part of its effect can be imaged as scaling. 2. TS FCs use linear functions of i/p vars. as rule consequent , Mamdani FCs use fuzzy sets. 3. TS FCs don’t need any Fuzzy Logic OR operators in fuzzy rules b’coz no identical rule consequents. 4. TS FCs have only one fuzzy inference method (no fuzzy inference in strict sense, as no consequent fuzzy sets to be operated / shaped acc. to any implication), but many choices exist for Mamdani FCs, depending on type of implication 25 used.

5. Mamdani FC uses fuzzy sets as rule consequent, so fuzzy rules more intuitive & more easily extractable from expert knowledge & experience. TS FC rule scheme not intuitive & has little linguistic meaning; expert knowledge & experience use also difficult. 6. Mamdani FC more tunable & economic as rule consequent has clear meaning & intuitively relates to system control performance. 7. TS FC has many design parameters in rule consequent; difficult to determine & tune due to lack of linguistic & intuitive meaning of parameters as also their disconnections to sys ctrl performance. 8. For both FCs, no. of dsgn parameters rises quickly with inc. in no. of i/p & o/p vars. , but situation worsens faster for TS 26 FCs

v. ADAPTIVE FUZZY CONTROL 1. Rationale: • Most real-world processes: time-varying & / or non-linear; parameters alter either over time or as operating pt. alters. • Linear Conventional ctlrs tuned to give good performance for ltd. time or at particular operating pt. ; thus to be re-tuned if operating pt. changes, or if process changes with time. • Necessity to retune: drives the need for Adaptive Ctlrs that can automatically retune to match the current process chrs. • FKBCs: non-linear, so cope with certain amt. of process non -linearity, but such design is difficult, especially if significant non-linearity. Also, rules of FKBC do not have temporal component, so can not cope with process changes with time. ü Hence adapt FKBC as well. 27

28

THANKS 29