Nonlinear Filtering for Extracting Orientation and Tracing Tubular

Nonlinear Filtering for Extracting Orientation and Tracing Tubular Structures in 2 -D Medical Images H. E. Çetingül, R. Vidal, G. Plank, N. Trayanova IEEE ISBI’ 08 - 05/15/2008

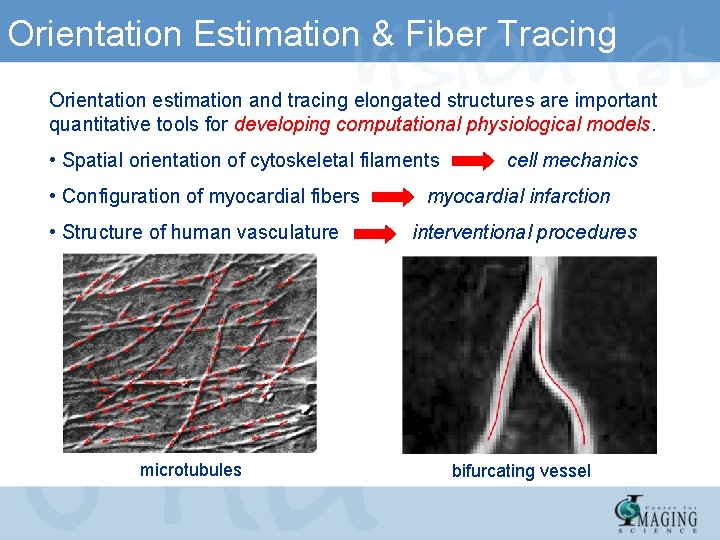
Orientation Estimation & Fiber Tracing Orientation estimation and tracing elongated structures are important quantitative tools for developing computational physiological models. • Spatial orientation of cytoskeletal filaments • Configuration of myocardial fibers cell mechanics myocardial infarction • Structure of human vasculature interventional procedures microtubules bifurcating vessel

Prior Work (1/2) • Related to a primal problem in image processing: edge detection • Several efforts in the image processing and computer vision communities to introduce fast and robust edge detection algorithms. – – Image gradient (Karlon et al ABE’ 99) Image Hessian (Frangi et al. MICCAI’ 98, Krissian et al, CVIU’ 00) Structure tensor (Aach et al. TIP’ 06) Combined methods (Sargin et al. ISBI’ 07) • Problems: 1) High sensitivity to noise and scale 2) Inability to superimposed orientations

Prior Work (2/2) Filtering techniques to solve the aforementioned problems and to detect overlaid structures. • Derivative-of-Gaussian (Do. G) filters • Quadrature filters, steerable filters (Freeman PAMI‘ 91, Simoncelli TIP‘ 96) • Multiscale elongated filters (Galun et al ICCV’ 07). • Extraction of local intensity profile (Qian et al. ICCV’ 07) • Isotropic nonlinear filtering that avoids the computation of image derivatives (Liu et al. TIP’ 06)

Contributions We present a nonlinear filtering technique that 1. avoids computing image derivatives, 2. is capable of analyzing complexities such as bifurcations, crossings, 3. estimates orientation by integrating local directional profile with intensity coherence along the structure of interest, 4. tracks elongated structures using the estimated orientation as well as preserving local smoothness of the resulting curvilinear structure, 5. provides promising results on analyzing myocardial fibers, microtubules, and vascular structures, 6. can be easily extended to 3 -D structures and diffusion tensor data.

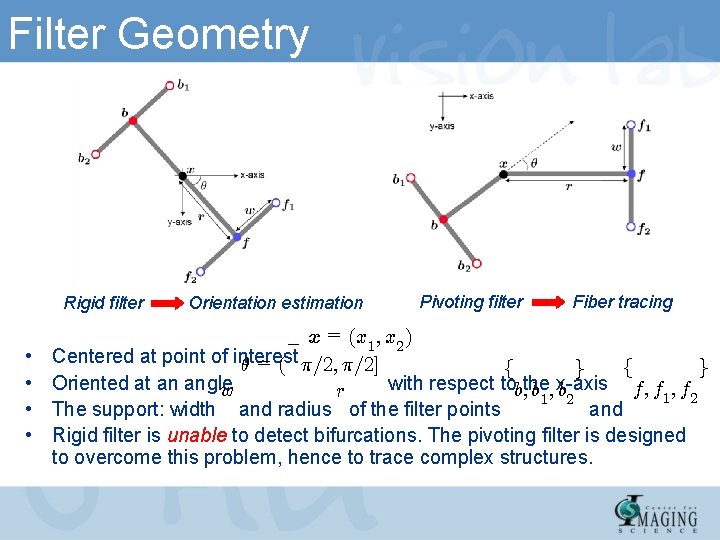
Filter Geometry Rigid filter • • Orientation estimation Pivoting filter Fiber tracing ¡ x = (x 1 ; x 2 ) Centered at point of interest µ = ( ¼=2; ¼=2] f g Oriented at an angle with respect tob; the f; f 1 ; f 2 w b 1 ; x-axis b 2 r The support: width and radius of the filter points and Rigid filter is unable to detect bifurcations. The pivoting filter is designed to overcome this problem, hence to trace complex structures.

Filter Photometry b 1 b b 2 x f 1 f hx (µ) = ( f ¡ ¡ j j· fj 2 ¡ jj jg 1 if I(f ) I(b) min I(bi ) I(b) ; I(fi ) I(f ) i=1; 2 0 otherwise: x µ “Voting scheme” At each pixel , the filter detects a linear structure oriented along if the absolute value of the intensity variation along the structure is less than the minimum absolute intensity variation orthogonal to the structure. D. Geman and B. Jedynak, “An Active Testing Model for Tracking Roads in Satellite Images, ” IEEE PAMI vol. 18, no. 1, 1998.

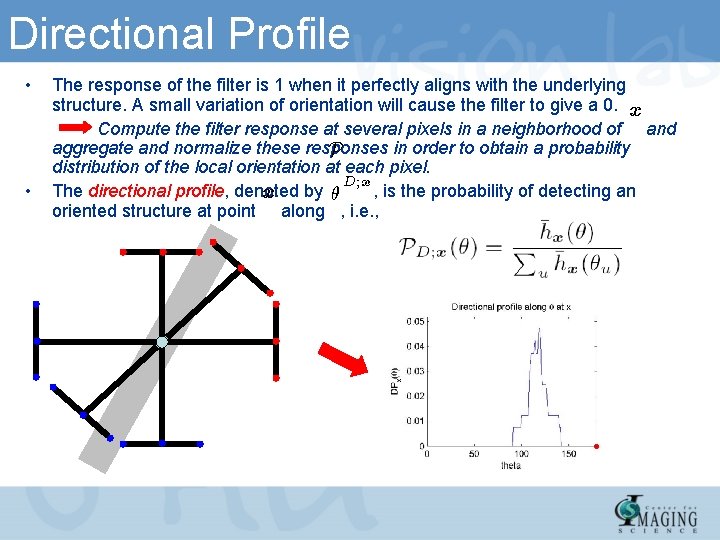
Directional Profile • • The response of the filter is 1 when it perfectly aligns with the underlying structure. A small variation of orientation will cause the filter to give a 0. x Compute the filter response at several pixels in a neighborhood of and aggregate and normalize these responses in order to obtain a probability P distribution of the local orientation at each pixel. D; x The directional profile, denoted , is the probability of detecting an x by µ oriented structure at point along , i. e. ,

Intensity Coherence b 1 • An alternative way of estimating local orientation in an image is to find image directions along which the intensity variation is small. Building a profile that measures the intensity coherence along a particular direction. • The sum of the absolute intensity difference remains low if 1) pivoting portion aligns with the true fiber, 2) the points for which the difference is computed are selected from the pivoting portion. b b 2 x f f f 2 1

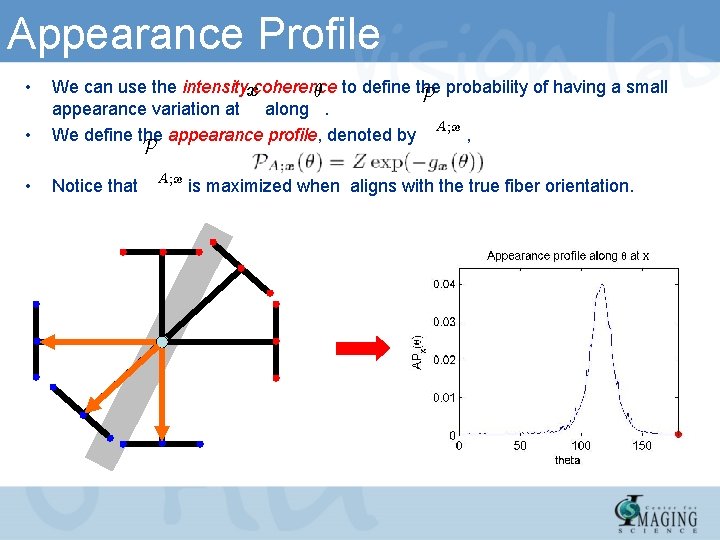
Appearance Profile • • We can use the intensityxcoherence µ to define the P probability of having a small appearance variation at along. A; x We define the appearance profile, denoted by , • Notice that P A; x is maximized when aligns with the true fiber orientation.

Local Orientation Estimation • Extraction of local orientation is performed by analyzing the distribution of fibers at some user-specified points. P P D; x A; x • The directional profile and the appearancexprofile µ probability of having a locally linear structure at along. reflect the P • We utilize the rigid filter to build profiles, and obtain µ x the aforementioned O; x the orientation profile at Palong £ as. P P (µ) = D; x (µ) O; x A; x • The modes, i. e. , local maxima, of the orientation profile give the candidate orientations.

Fiber Tracing x 1 f g x 1 ; x 2 ; x 3 ; : : : x 2 • Given and , our algorithm successively locates on the fiber and represents the resulting structure as the ordered set of those points. • At i-th step, given xi¡ 1 and xi x ^i+1 f = xi+1 b = xi¡ 1 x = xi Build P a^ pivoting filter, with , and. We then x i+1 choose as the point along the direction that maximizes the tracing T ; xi P £ P profile, which is defined as £ P (µ) = D; x (µ) °x (µ) T ; x A; x i i • The tracing profile favors both the local smoothness of the resulting structure as well as alignment with the directional profile and the appearance profile. The modes of the tracing profile give the candidate orientations to be tracked.

Mode Detection Gaussian Mixture Models (GMMs) • The number of Gaussian components corresponds to the maximum number of branches a fiber can divide into at a point. • Locating the underlying orientations at a point is equivalent to computing the parameters of the mixture model. • In particular, the means of the Gaussian distributions are the candidate orientations.

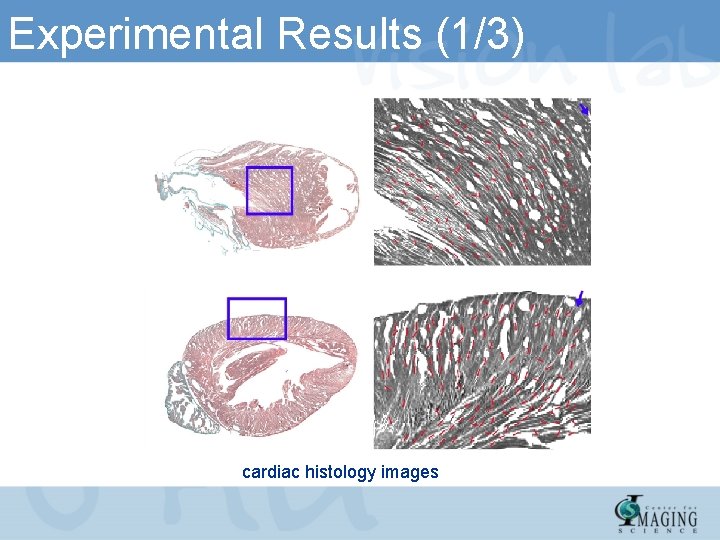
Experimental Results (1/3) cardiac histology images

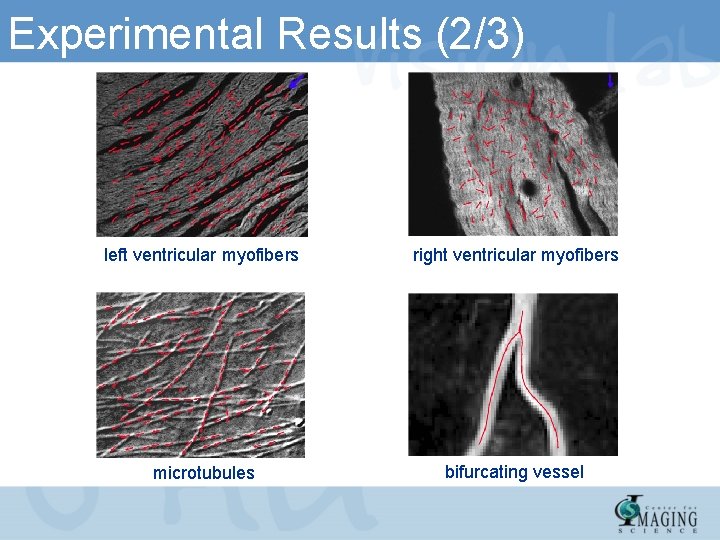
Experimental Results (2/3) left ventricular myofibers right ventricular myofibers microtubules bifurcating vessel

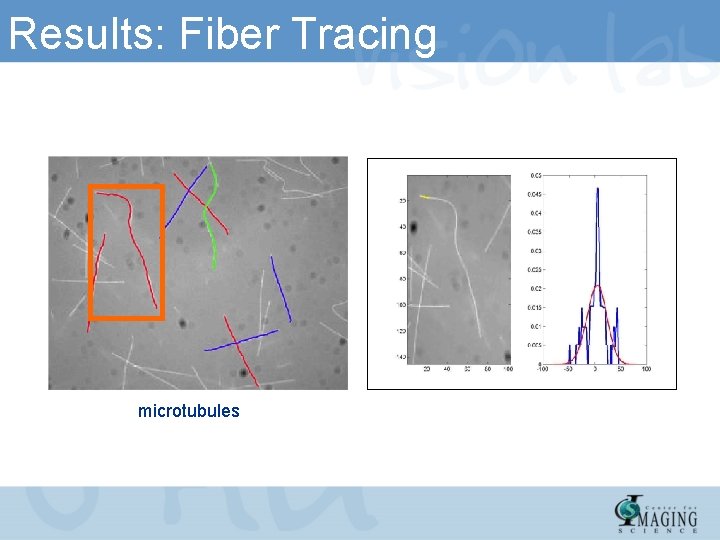
Results: Fiber Tracing microtubules

Current research Tracing of the 3 -D Purkinje network from MRI data manual tracing of the Purkinje network

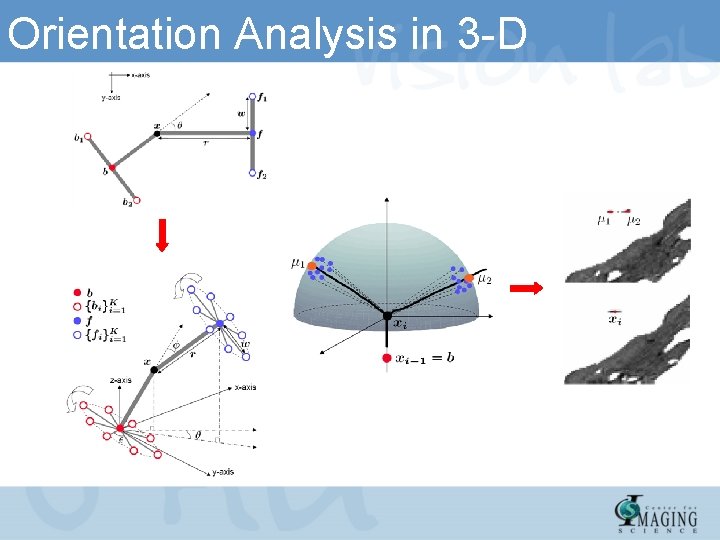
Orientation Analysis in 3 -D

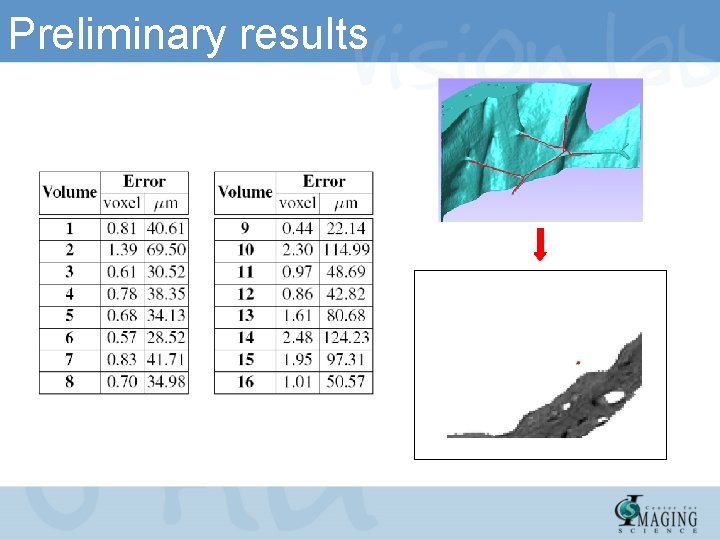
Preliminary results

Thanks… Questions? Comments? CONTACT: Hasan Ertan Çetingül, René Vidal, Gernot Plank, Natalia Trayanova {ertan, rvidal, gernot. plank, ntrayanova}@jhu. edu