Nonlinear Dimensionality Reduction Presented by Dragana Veljkovic Overview

Nonlinear Dimensionality Reduction Presented by Dragana Veljkovic

Overview Curse-of-dimensionality n Dimension reduction techniques n Isomap n Locally linear embedding (LLE) n Problems and improvements n 2

Problem description n n Large amount of data being collected leads to creation of very large databases Most problems in data mining involve data with a large number of measurements (or dimensions) E. g. Protein matching, fingerprint recognition, meteorological predictions, satellite image repositories Reducing dimensions increases capability of extracting knowledge 3

Problem definition Original high dimensional data: X = (x 1, …, xn) where xi=(xi 1, …, xip)T n underlying low dimensional data: Y = (y 1, …, yn) where yi=(yi 1, …, yiq)T and q<<p n n Assume X forms a smooth low dimensional manifold in high dimensional space Find the mapping that captures the important features Determine q that can best describe the data 4

Different approaches n n Local or Shape preserving Global or Topology preserving Local embeddings Local – simplify representation of each object regardless of the rest of the data ¨ Features selected retain most of the information ¨ Fourier decomposition, wavelet decomposition, piecewise constant approximation, etc. 5

Global or Topology preserving n Mostly used for visualization and classification ¨ PCA or KL decomposition ¨ MDS ¨ SVD ¨ ICA 6

Local embeddings (LE) n n Overlapping local neighborhoods, collectively analyzed, can provide information on global geometry LE preserves the local neighborhood of each object preserving the global distances through the nonneighboring objects Isomap and LLE 7

Another classification n Linear and Non Linear methods 8

Neighborhood Two ways to select neighboring objects: ¨k nearest neighbors (k-NN) – can make nonuniform neighbor distance across the dataset ¨ ε-ball – prior knowledge of the data is needed to make reasonable neighborhoods; size of neighborhood can vary 9

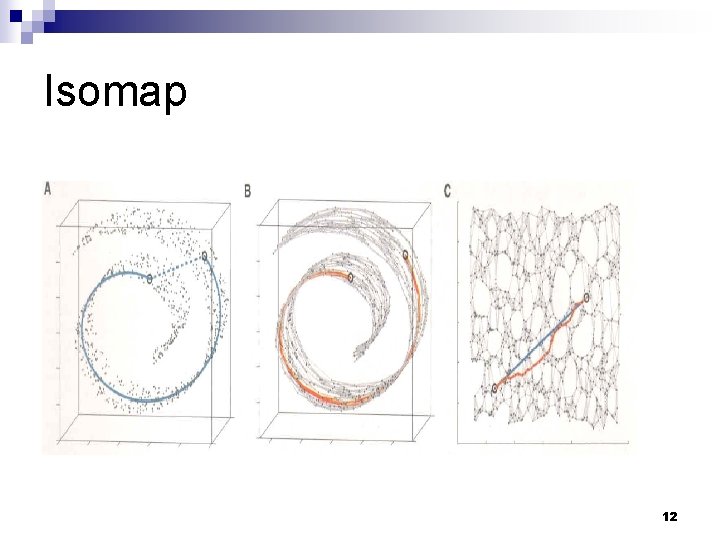
Isomap – general idea n n n Only geodesic distances reflect the true low dimensional geometry of the manifold MDS and PCA see only Euclidian distances and there for fail to detect intrinsic low-dimensional structure Geodesic distances are hard to compute even if you know the manifold In a small neighborhood Euclidian distance is a good approximation of the geodesic distance For faraway points, geodesic distance is approximated by adding up a sequence of “short hops” between neighboring points 10

Isomap algorithm n n Find neighborhood of each object by computing distances between all pairs of points and selecting closest Build a graph with a node for each object and an edge between neighboring points. Euclidian distance between two objects is used as edge weight Use a shortest path graph algorithm to fill in distance between all non-neighboring points Apply classical MDS on this distance matrix 11

Isomap 12

Isomap on face images 13

Isomap on hand images 14

Isomap on written two-s 15

Isomap - summary n Inherits features of MDS and PCA: guaranteed asymptotic convergence to true structure ¨ Polynomial runtime ¨ Non-iterative ¨ Ability to discover manifolds of arbitrary dimensionality ¨ n n n Perform well when data is from a single well sampled cluster Few free parameters Good theoretical base for its metrics preserving properties 16

Problems with Isomap Embeddings are biased to preserve the separation of faraway points, which can lead to distortion of local geometry n Fails to nicely project data spread among multiple clusters n Well-conditioned algorithm but computationally expensive for large datasets n 17

Improvements to Isomap Conformal Isomap – capable of learning the structure of certain curved manifolds n Landmark Isomap – approximates large global computations by a much smaller set of calculation n Reconstruct distances using k/2 closest objects, as well as k/2 farthest objects n 18

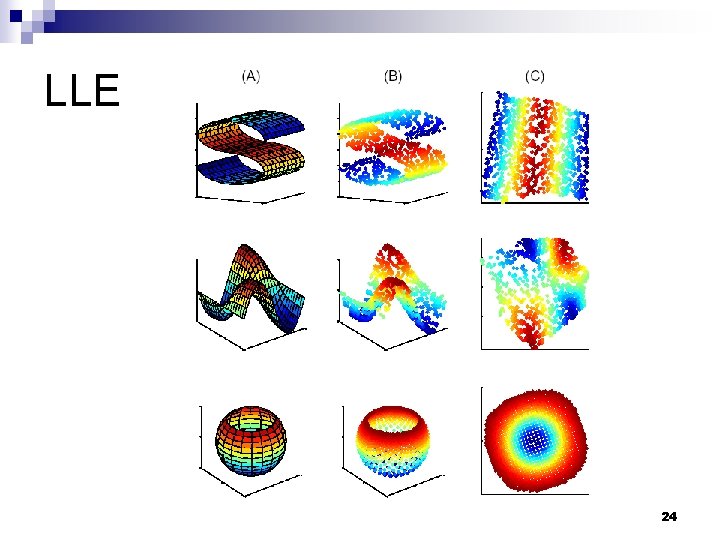
Locally Linear Embedding (LLE) n Isomap attempts to preserve geometry on all scales, mapping nearby points close and distant points far away from each other n LLE attempts to preserve local geometry of the data by mapping nearby points on the manifold to nearby points in the low dimensional space Computational efficiency Representational capacity n n 19

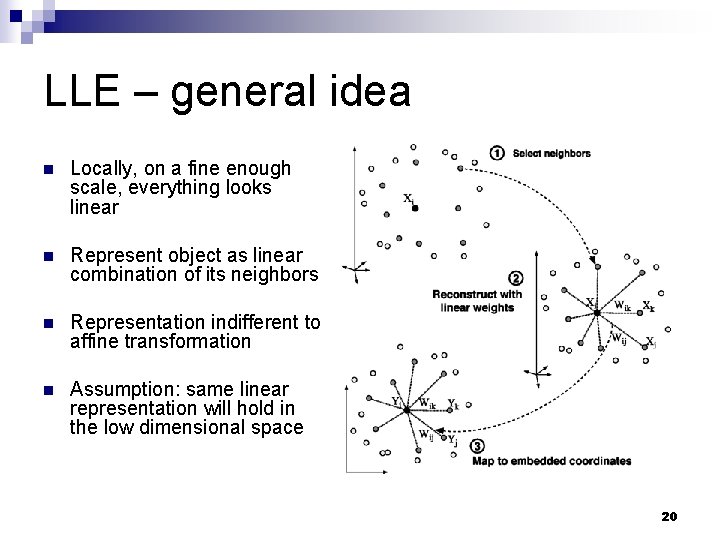
LLE – general idea n Locally, on a fine enough scale, everything looks linear n Represent object as linear combination of its neighbors n Representation indifferent to affine transformation n Assumption: same linear representation will hold in the low dimensional space 20

LLE – matrix representation X = W*X where n X is p*n matrix of original data n W is n*n matrix of weights and Wij =0 if Xj is not neighbor of Xi ¨ rows of W sum to one ¨ Need to solve system Y = W*Y n Y is q*n matrix of underlying low dimensional data n Minimize error: 21

LLE - algorithm n Find k nearest neighbors in X space n Solve for reconstruction weights W n Compute embedding coordinates Y using weights W: ¨ create sparse matrix M = (I-W)'*(I-W) ¨ Compute bottom q+1 eigenvectors of M ¨ Set i-th row of Y to be i+1 smallest eigen vector 22

Numerical Issues Covariance matrix used to compute W can be ill-conditioned, regularization needs to be used n Small eigen values are subject to numerical precision errors and to getting mixed n But, sparse matrices used in this algorithm make it much faster then Isomap n 23

LLE 24

LLE – effect of neighborhood size 25

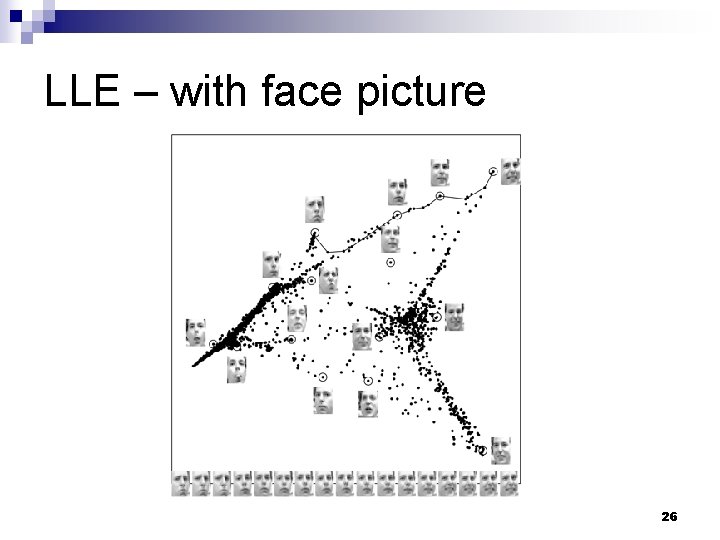
LLE – with face picture 26

LLE – Lips pictures 27

PCA vs. LLE 28

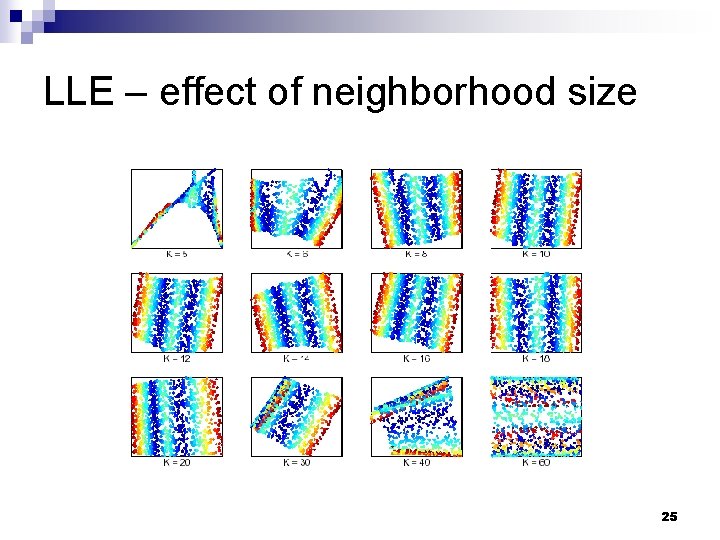
Problems with LLE If data is noisy, sparse or weakly connected coupling between faraway points can be attenuated n Most common failure of LLE is mapping close points that are faraway in original space – arising often if manifold is undersampled n Output strongly depends on selection of k n 29

References n Roweis, S. T. and L. K. Saul (2000). "Nonlinear dimensionality reduction by locally linear embedding " Science 290(5500): 2323 -2326. n Tenenbaum, J. B. , V. de Silva, et al. (2000). "A global geometric framework for nonlinear dimensionality reduction " Science 290(5500): 2319 -2323. n Vlachos, M. , C. Domeniconi, et al. (2002). "Non-linear dimensionality reduction techniques for classification and visualization. " Proc. of 8 th SIGKDD, Edmonton, Canada. n de Silva, V. and Tenenbaum, J. (2003). “Local versus global methods for nonlinear dimensionality reduction”, Advances in Neural Information Processing Systems, 15. 30

Questions? 31