Nonlinear Analysis Performance Based Design Nonlinear Analysis Performance

Nonlinear Analysis & Performance Based Design

Nonlinear Analysis & Performance Based Design
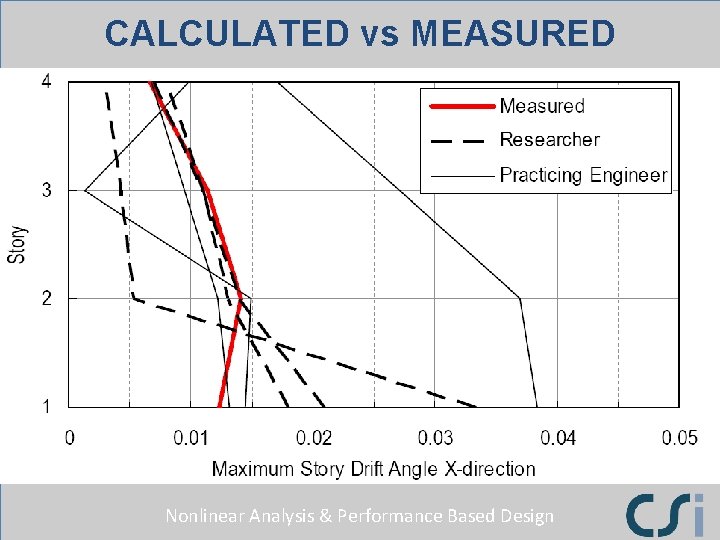
CALCULATED vs MEASURED Nonlinear Analysis & Performance Based Design
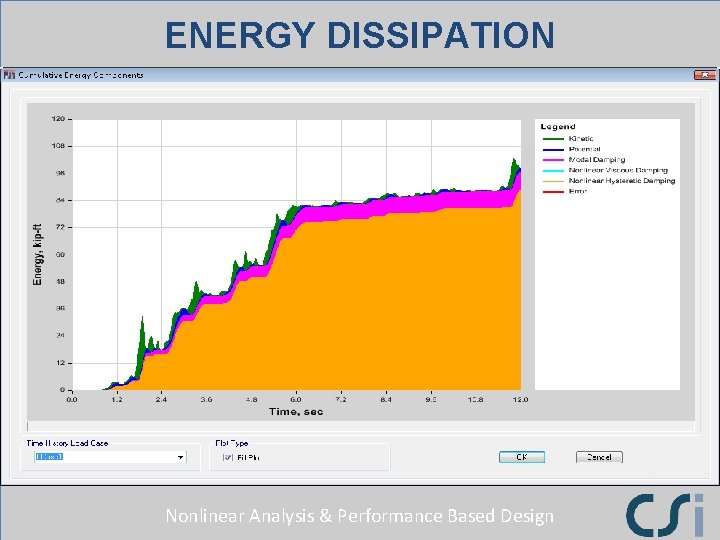
ENERGY DISSIPATION Nonlinear Analysis & Performance Based Design
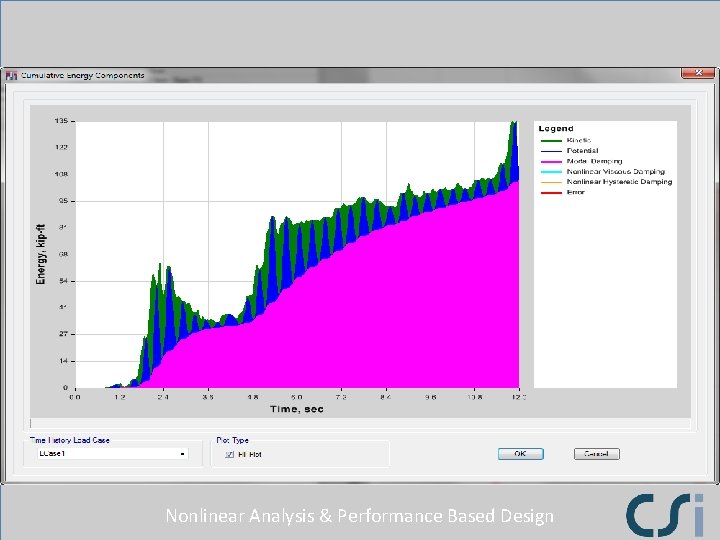
Nonlinear Analysis & Performance Based Design
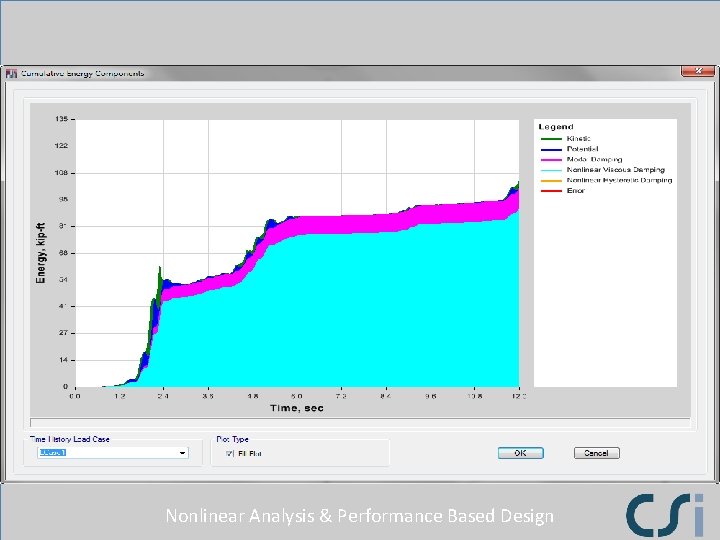
Nonlinear Analysis & Performance Based Design
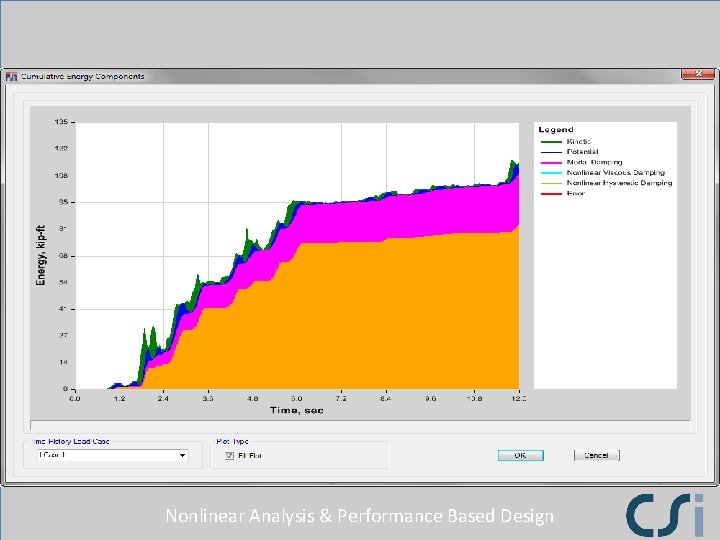
Nonlinear Analysis & Performance Based Design

IMPLICIT NONLINEAR BEHAVIOR Nonlinear Analysis & Performance Based Design
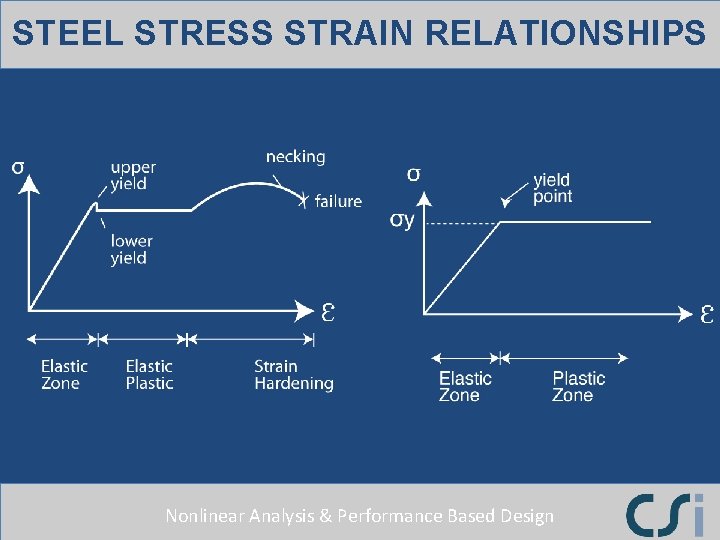
STEEL STRESS STRAIN RELATIONSHIPS Nonlinear Analysis & Performance Based Design

INELASTIC WORK DONE! Nonlinear Analysis & Performance Based Design

CAPACITY DESIGN STRONG COLUMNS & WEAK BEAMS IN FRAMES REDUCED BEAM SECTIONS LINK BEAMS IN ECCENTRICALLY BRACED FRAMES BUCKLING RESISTANT BRACES AS FUSES RUBBER-LEAD BASE ISOLATORS HINGED BRIDGE COLUMNS HINGES AT THE BASE LEVEL OF SHEAR WALLS ROCKING FOUNDATIONS OVERDESIGNED COUPLING BEAMS OTHER SACRIFICIAL ELEMENTS Nonlinear Analysis & Performance Based Design
STRUCTURAL COMPONENTS Nonlinear Analysis & Performance Based Design
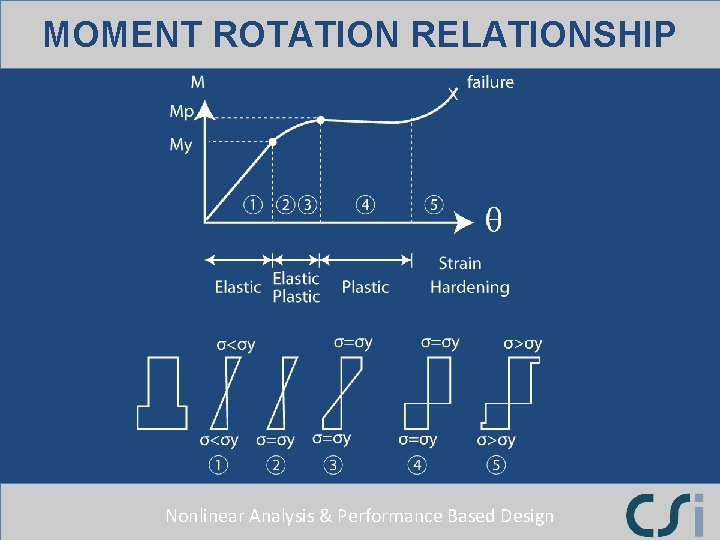
MOMENT ROTATION RELATIONSHIP Nonlinear Analysis & Performance Based Design
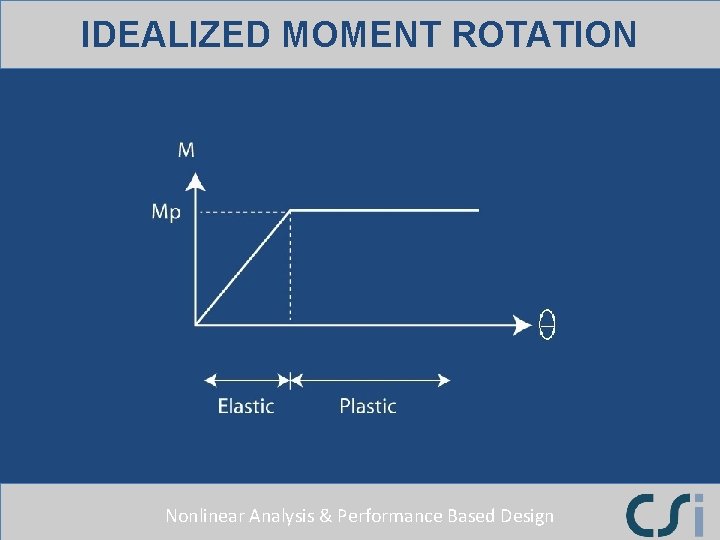
IDEALIZED MOMENT ROTATION Nonlinear Analysis & Performance Based Design
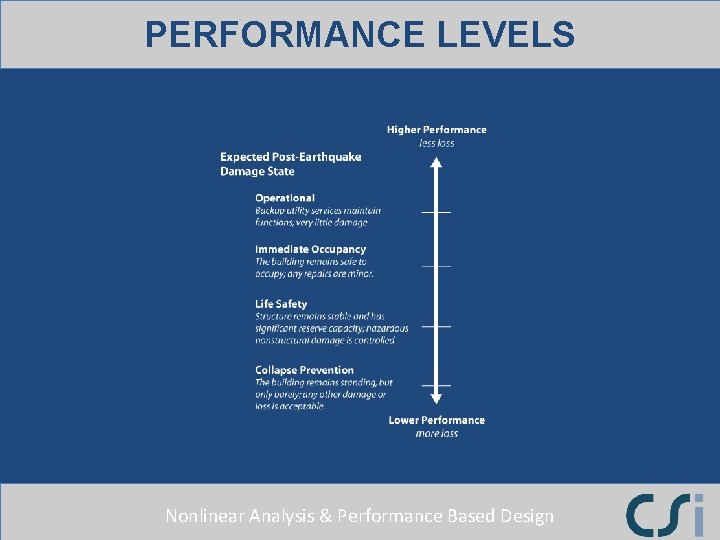
PERFORMANCE LEVELS Nonlinear Analysis & Performance Based Design
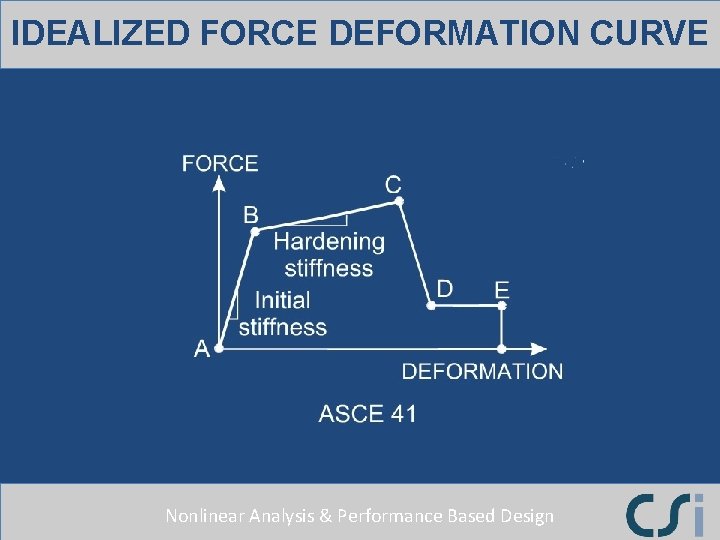
IDEALIZED FORCE DEFORMATION CURVE Nonlinear Analysis & Performance Based Design
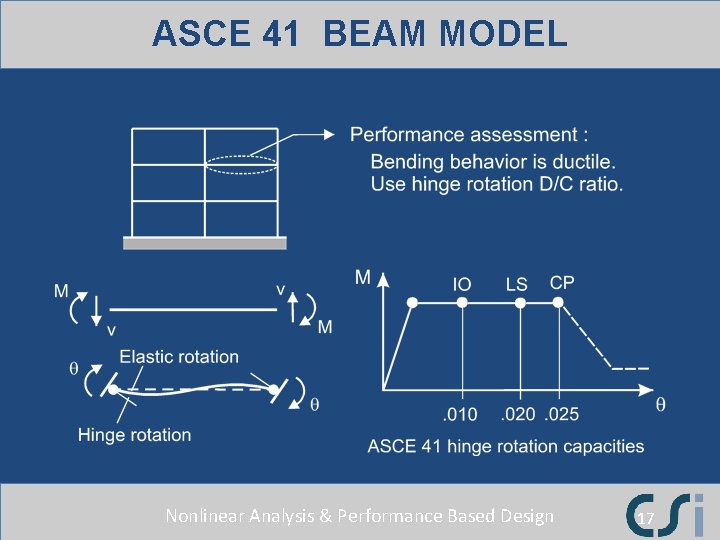
ASCE 41 BEAM MODEL Nonlinear Analysis & Performance Based Design 17

ASCE 41 ASSESSMENT OPTIONS • Linear Static Analysis • Linear Dynamic Analysis (Response Spectrum or Time History Analysis) • Nonlinear Static Analysis (Pushover Analysis) • Nonlinear Dynamic Time History Analysis (NDI or FNA) Nonlinear Analysis & Performance Based Design

STRENGTH vs DEFORMATION ELASTIC STRENGTH DESIGN - KEY STEPS CHOSE DESIGN CODE AND EARTHQUAKE LOADS DESIGN CHECK PARAMETERS STRESS/BEAM MOMENT GET ALLOWABLE STRESSES/ULTIMATE– PHI FACTORS CALCULATE STRESSES – LOAD FACTORS (ST RS TH) CALCULATE STRESS RATIOS INELASTIC DEFORMATION BASED DESIGN -- KEY STEPS CHOSE PERFORMANCE LEVEL AND DESIGN LOADS – ASCE 41 DEMAND CAPACITY MEASURES – DRIFT/HINGE ROTATION/SHEAR GET DEFORMATION AND FORCE CAPACITIES CALCULATE DEFORMATION AND FORCE DEMANDS (RS OR TH) CALCULATE D/C RATIOS – LIMIT STATES Nonlinear Analysis & Performance Based Design
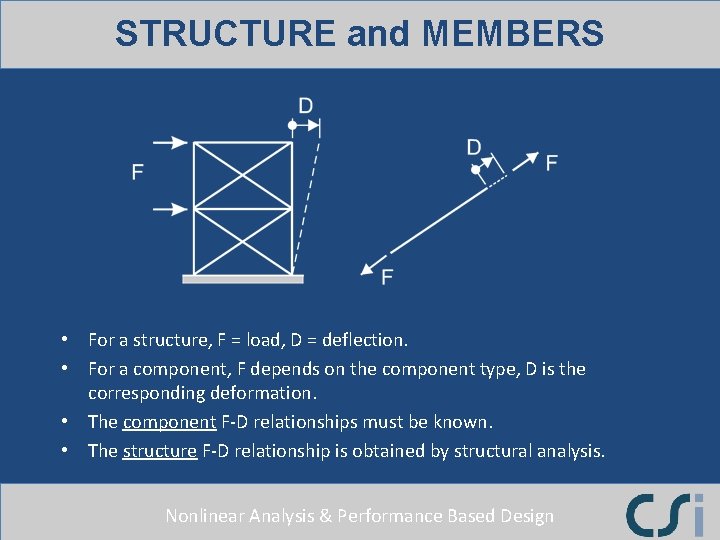
STRUCTURE and MEMBERS • For a structure, F = load, D = deflection. • For a component, F depends on the component type, D is the corresponding deformation. • The component F-D relationships must be known. • The structure F-D relationship is obtained by structural analysis. Nonlinear Analysis & Performance Based Design

FRAME COMPONENTS • For each component type we need : Reasonably accurate nonlinear F-D relationships. Reasonable deformation and/or strength capacities. • We must choose realistic demand-capacity measures, and it must be feasible to calculate the demand values. • The best model is the simplest model that will do the job. Nonlinear Analysis & Performance Based Design

F-D RELATIONSHIP Nonlinear Analysis & Performance Based Design
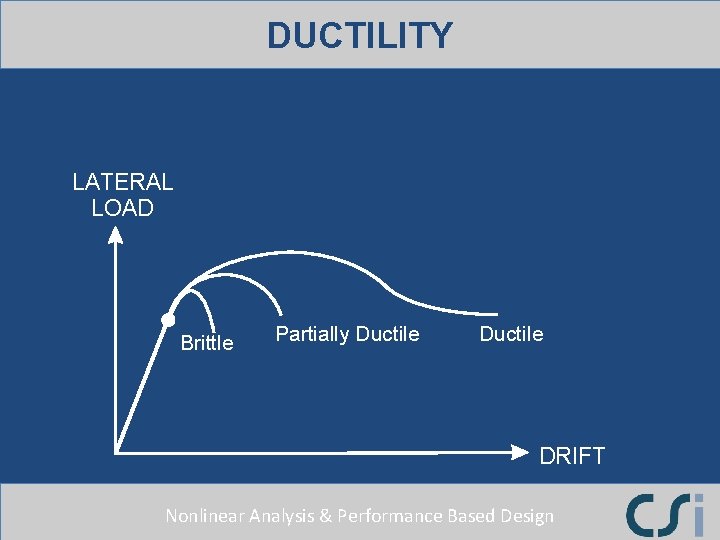
DUCTILITY LATERAL LOAD Brittle Partially Ductile DRIFT Nonlinear Analysis & Performance Based Design

ASCE 41 - DUCTILE AND BRITTLE Nonlinear Analysis & Performance Based Design
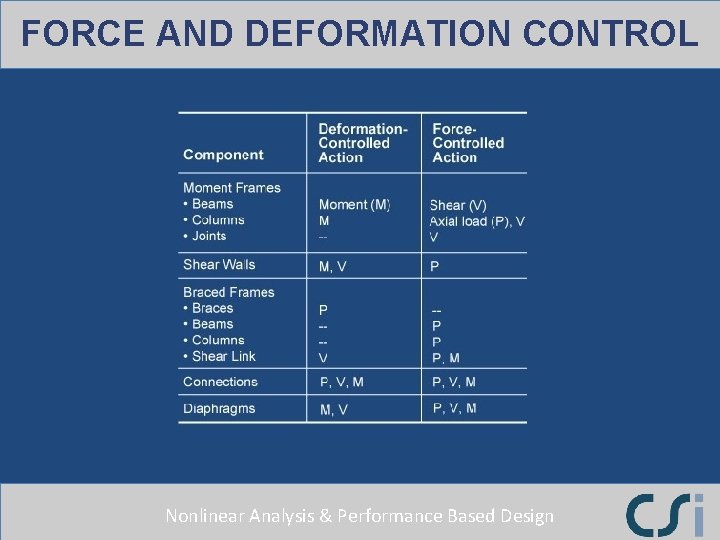
FORCE AND DEFORMATION CONTROL Nonlinear Analysis & Performance Based Design
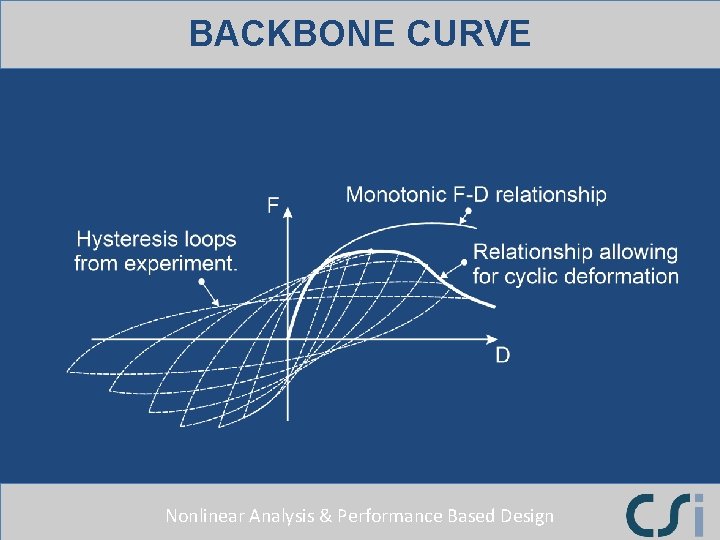
BACKBONE CURVE Nonlinear Analysis & Performance Based Design
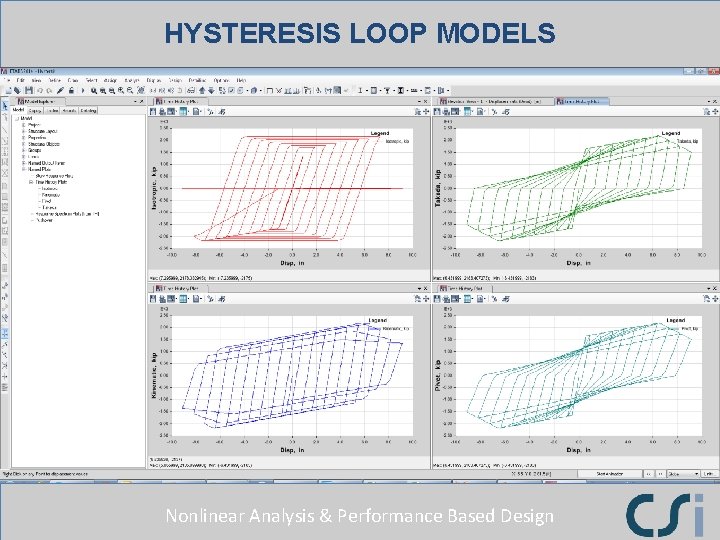
HYSTERESIS LOOP MODELS Nonlinear Analysis & Performance Based Design

STRENGTH DEGRADATION Nonlinear Analysis & Performance Based Design

ASCE 41 DEFORMATION CAPACITIES • • This can be used for components of all types. It can be used if experimental results are available. ASCE 41 gives capacities for many different components. For beams and columns, ASCE 41 gives capacities only for the chord rotation model. Nonlinear Analysis & Performance Based Design
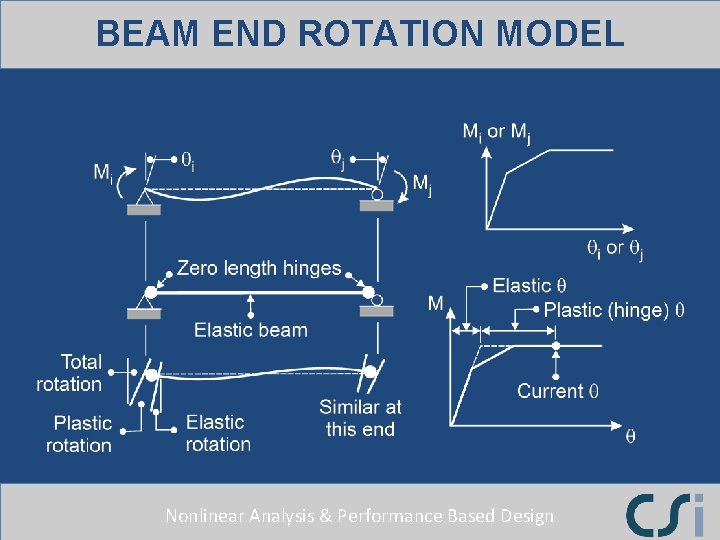
BEAM END ROTATION MODEL Nonlinear Analysis & Performance Based Design

PLASTIC HINGE MODEL • It is assumed that all inelastic deformation is concentrated in zerolength plastic hinges. • The deformation measure for D/C is hinge rotation. Nonlinear Analysis & Performance Based Design

PLASTIC ZONE MODEL • The inelastic behavior occurs in finite length plastic zones. • Actual plastic zones usually change length, but models that have variable lengths are too complex. • The deformation measure for D/C can be : - Average curvature in plastic zone. - Rotation over plastic zone ( = average curvature x plastic zone length). Nonlinear Analysis & Performance Based Design
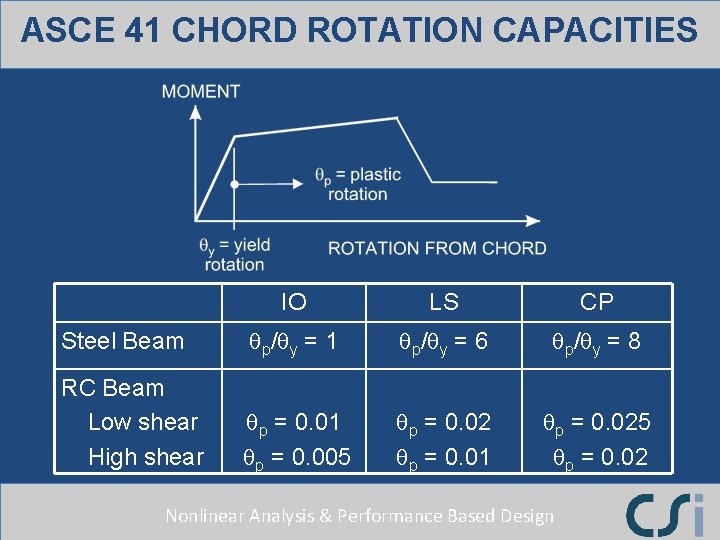
ASCE 41 CHORD ROTATION CAPACITIES IO LS CP Steel Beam qp/qy = 1 qp/qy = 6 qp/qy = 8 RC Beam Low shear High shear qp = 0. 01 qp = 0. 005 qp = 0. 02 qp = 0. 01 qp = 0. 025 qp = 0. 02 Nonlinear Analysis & Performance Based Design
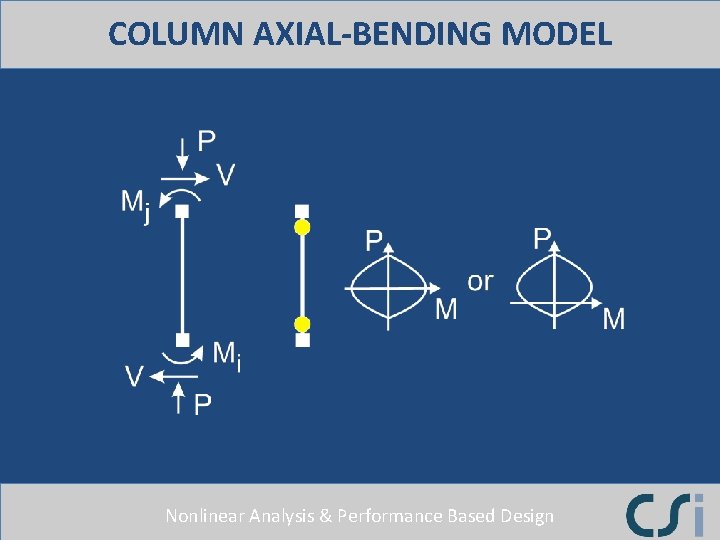
COLUMN AXIAL-BENDING MODEL Nonlinear Analysis & Performance Based Design
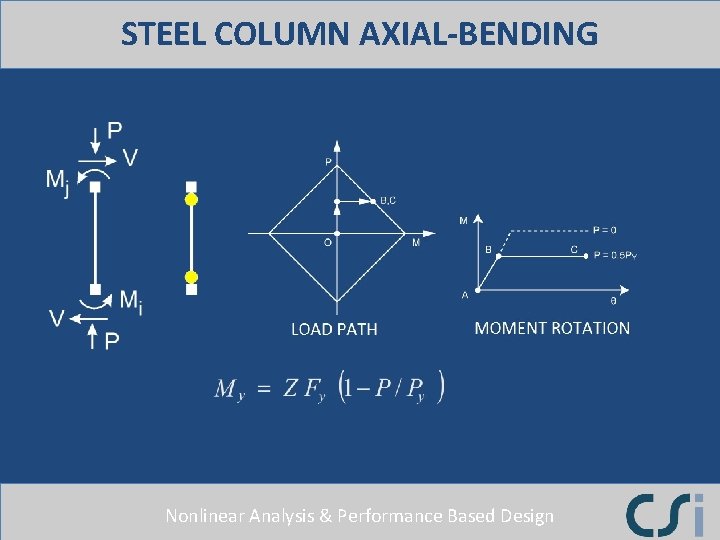
STEEL COLUMN AXIAL-BENDING Nonlinear Analysis & Performance Based Design
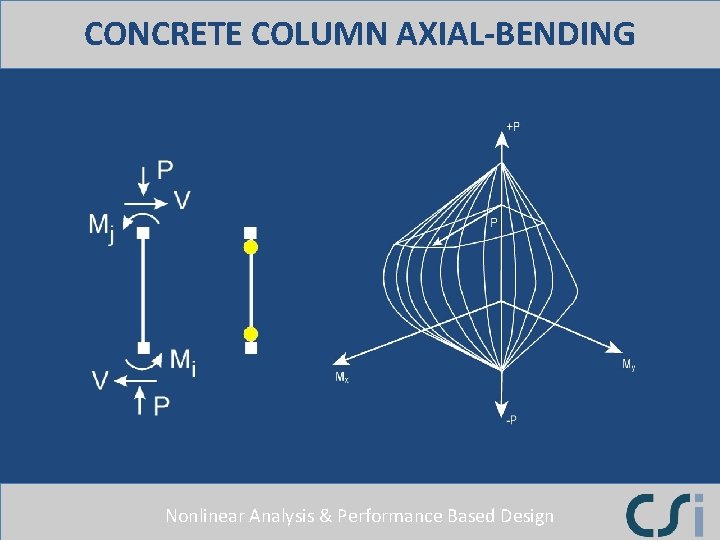
CONCRETE COLUMN AXIAL-BENDING Nonlinear Analysis & Performance Based Design
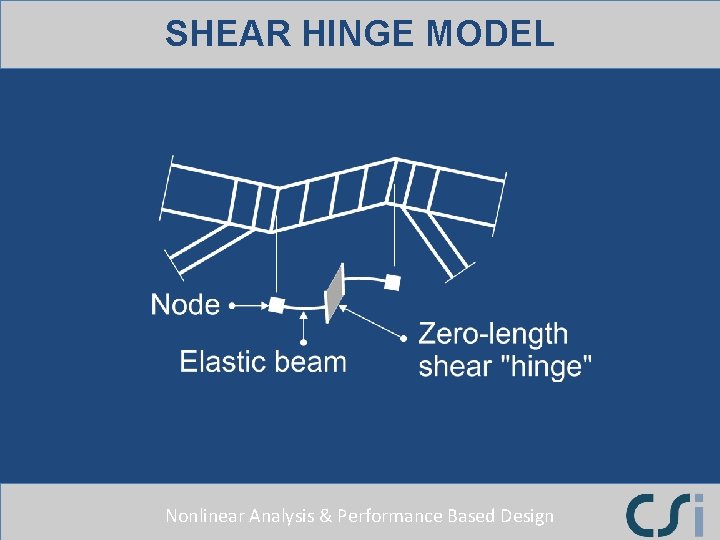
SHEAR HINGE MODEL Nonlinear Analysis & Performance Based Design
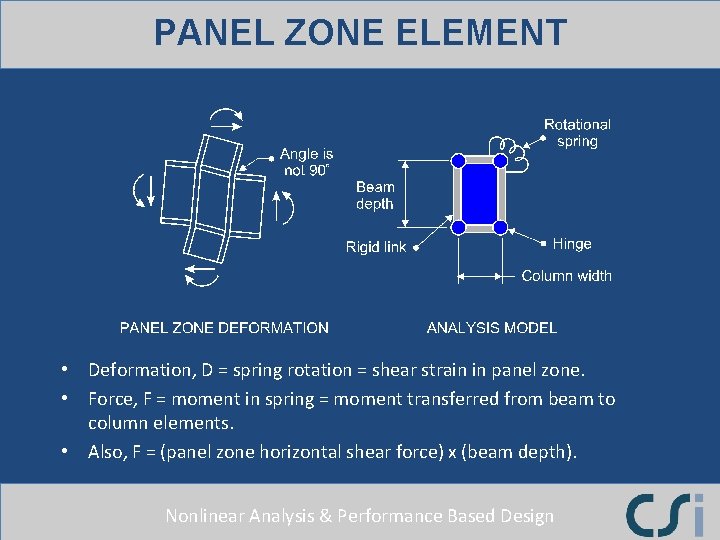
PANEL ZONE ELEMENT • Deformation, D = spring rotation = shear strain in panel zone. • Force, F = moment in spring = moment transferred from beam to column elements. • Also, F = (panel zone horizontal shear force) x (beam depth). Nonlinear Analysis & Performance Based Design

BUCKLING-RESTRAINED BRACE The BRB element includes “isotropic” hardening. The D-C measure is axial deformation. Nonlinear Analysis & Performance Based Design

BEAM/COLUMN FIBER MODEL The cross section is represented by a number of uni-axial fibers. The M-y relationship follows from the fiber properties, areas and locations. Stress-strain relationships reflect the effects of confinement Nonlinear Analysis & Performance Based Design
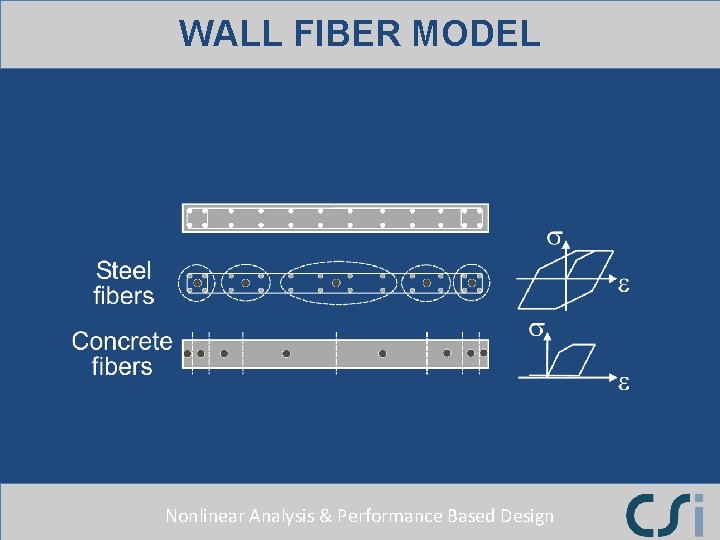
WALL FIBER MODEL Nonlinear Analysis & Performance Based Design
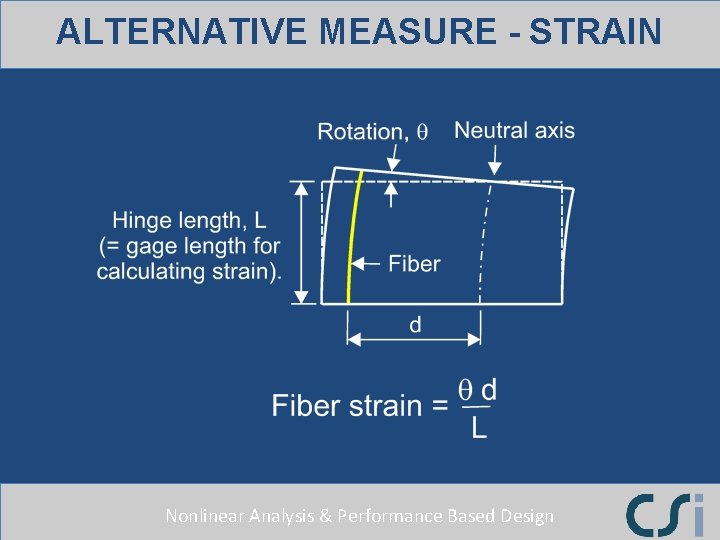
ALTERNATIVE MEASURE - STRAIN Nonlinear Analysis & Performance Based Design
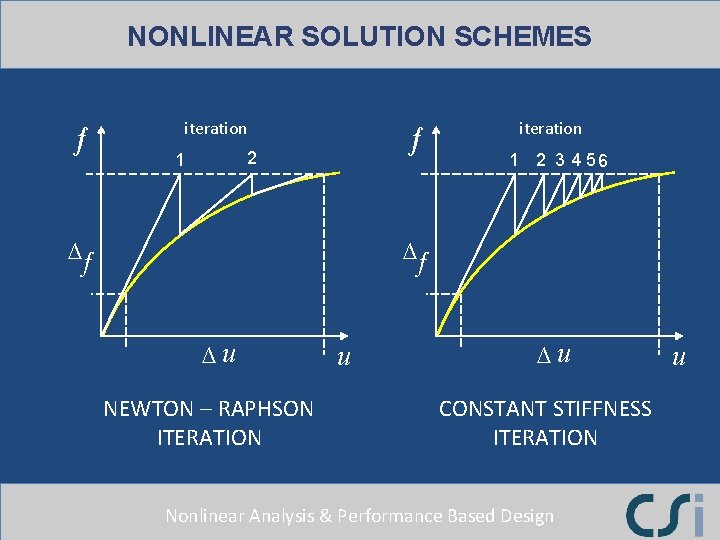
NONLINEAR SOLUTION SCHEMES ƒ iteration ƒ 2 1 ∆ƒ iteration 1 2 3 4 56 ∆ƒ ∆u NEWTON – RAPHSON ITERATION u ∆u CONSTANT STIFFNESS ITERATION Nonlinear Analysis & Performance Based Design u

CIRCULAR FREQUENCY +Y Y q 0 Radius, R -Y Nonlinear Analysis & Performance Based Design
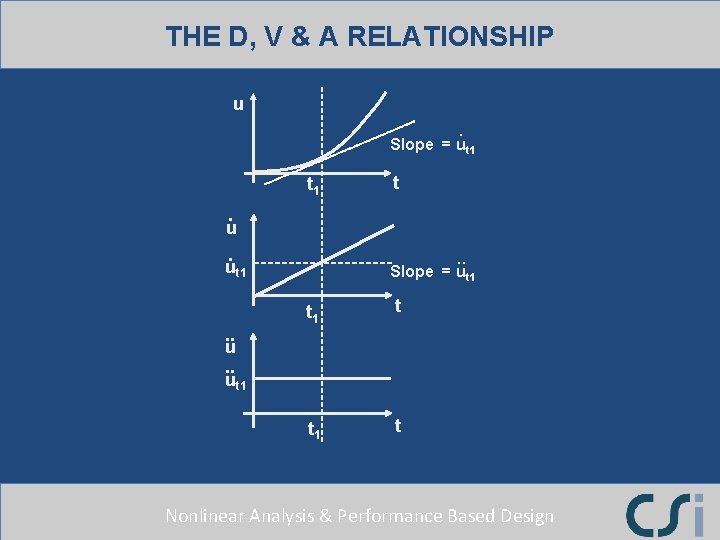
THE D, V & A RELATIONSHIP u. Slope = ut 1 t 1. u. ut 1 t . . Slope = ut 1 t Nonlinear Analysis & Performance Based Design

UNDAMPED FREE VIBRATION + ku = 0 & & mu ut = u 0 cos(wt) k where w = m Nonlinear Analysis & Performance Based Design

RESPONSE MAXIMA ut = u 0 cos(wt) t = -wu 0 sin(wt) u& & t = -w u 0 cos(wt) u& 2 2 = w & max u& u max Nonlinear Analysis & Performance Based Design
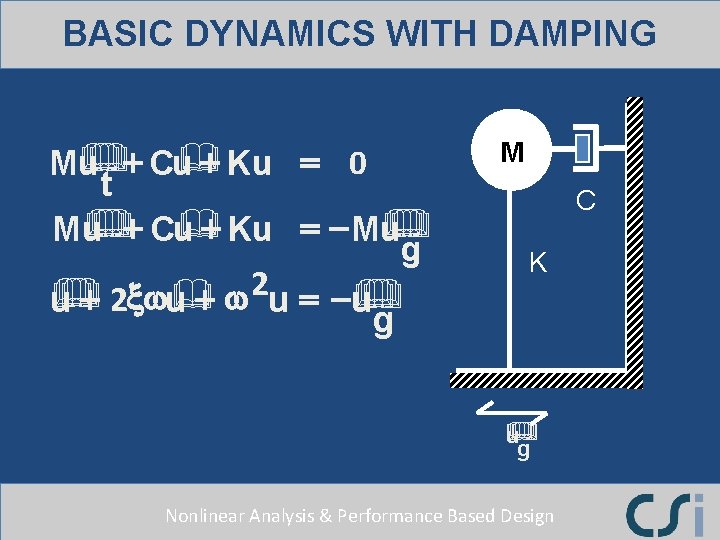
BASIC DYNAMICS WITH DAMPING & &+ Cu& + Ku = 0 Mu t & &+ Cu& & & + Ku = - Mu Mu g 2 & & & u + 2 xwu + w u = - u g M C K & & u g Nonlinear Analysis & Performance Based Design
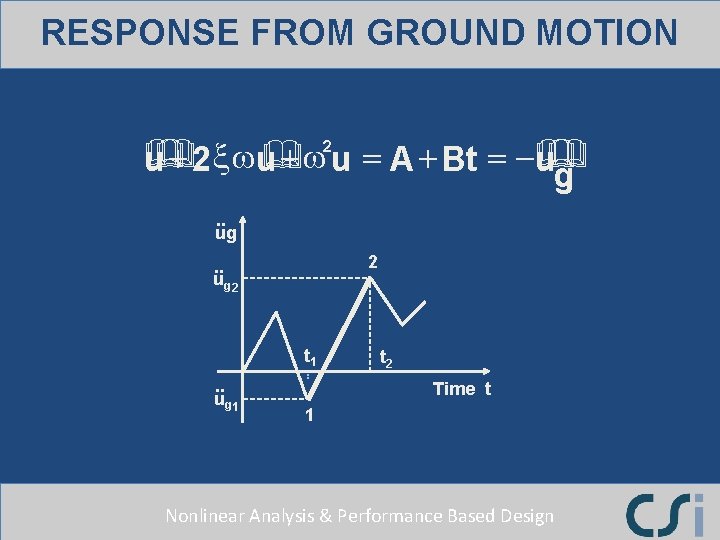
RESPONSE FROM GROUND MOTION 2 & & & u + 2 xwu + w u = A + Bt = -& u& g . . ug 2 . . u g 2 t 1. . u g 1 t 2 Time t 1 Nonlinear Analysis & Performance Based Design

DAMPED RESPONSE u& t = e + ut = - xwt { [u& t 1 B ] cos wd t 2 w 1 B B 2 & w xw + [A ut (ut )] sin d t } 2 1 1 wd w w 2 e - xwt { [ut 1 A 2 x. B + ] cos wd t 2 3 w w x A B(2 x 2 - 1) 1 + + wd t } [u& ] sin t 1 + xwut 1 wd w w 2 A 2 x. B Bt +[ + ] 2 3 2 w w w Nonlinear Analysis & Performance Based Design
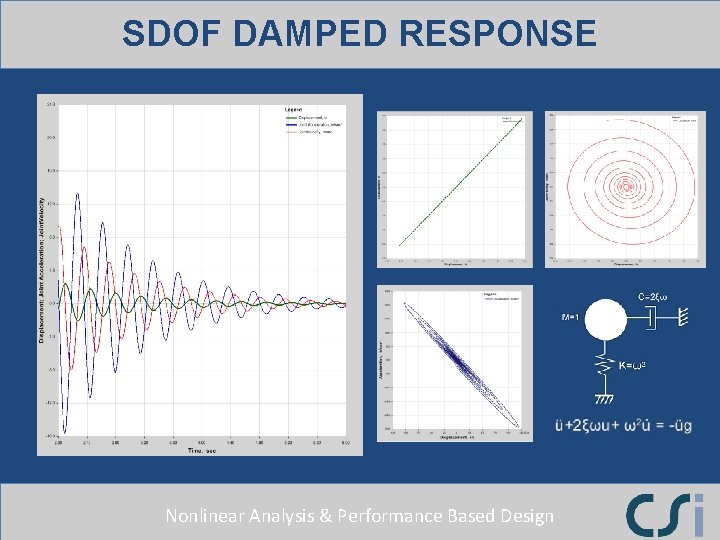
SDOF DAMPED RESPONSE Nonlinear Analysis & Performance Based Design
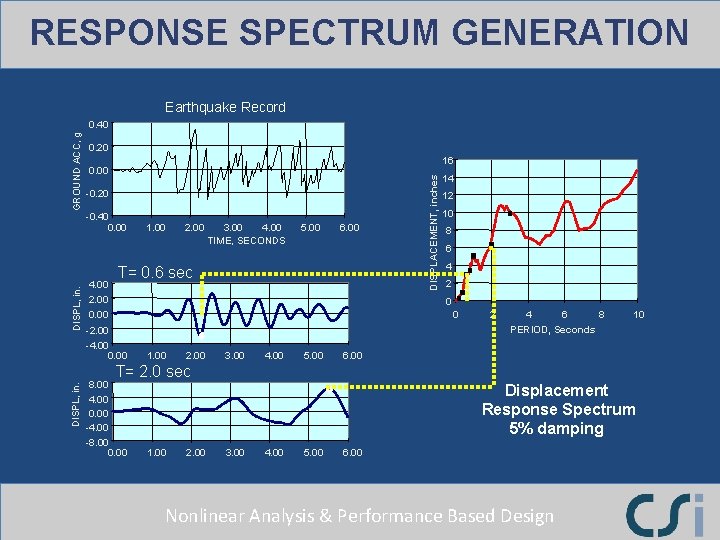
RESPONSE SPECTRUM GENERATION Earthquake Record 0. 20 16 0. 00 -0. 20 DISPL, in. -0. 40 0. 00 4. 00 1. 00 2. 00 3. 00 4. 00 TIME, SECONDS 5. 00 6. 00 T= 0. 6 sec 2. 00 0. 00 DISPLACEMENT, inches GROUND ACC, g 0. 40 14 12 10 8 6 4 2 0 0 -2. 00 -4. 00 0. 00 2 4 6 8 10 PERIOD, Seconds 1. 00 2. 00 3. 00 4. 00 5. 00 6. 00 DISPL, in. T= 2. 0 sec 8. 00 4. 00 0. 00 -4. 00 -8. 00 0. 00 Displacement Response Spectrum 5% damping 1. 00 2. 00 3. 00 4. 00 5. 00 6. 00 Nonlinear Analysis & Performance Based Design
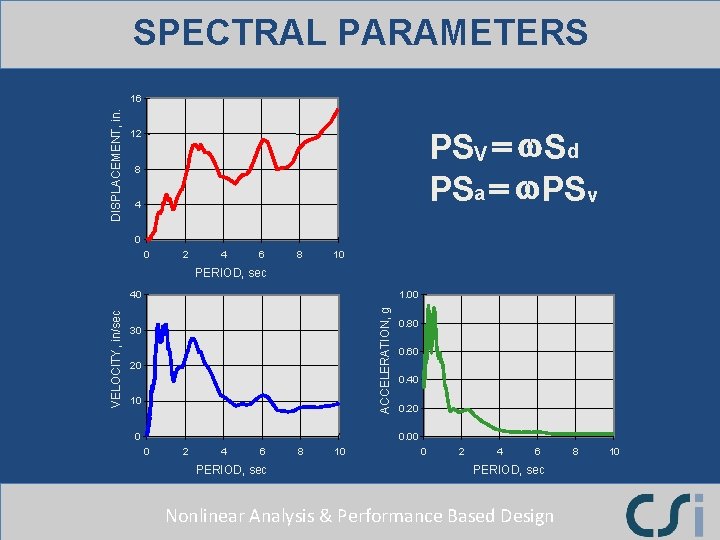
SPECTRAL PARAMETERS DISPLACEMENT, in. 16 PSV = w Sd PSa = w PSv 12 8 4 0 0 2 4 6 8 10 PERIOD, sec 1. 00 ACCELERATION, g VELOCITY, in/sec 40 30 20 10 0 0. 80 0. 60 0. 40 0. 20 0. 00 0 2 4 6 PERIOD, sec 8 10 0 2 4 6 PERIOD, sec Nonlinear Analysis & Performance Based Design 8 10
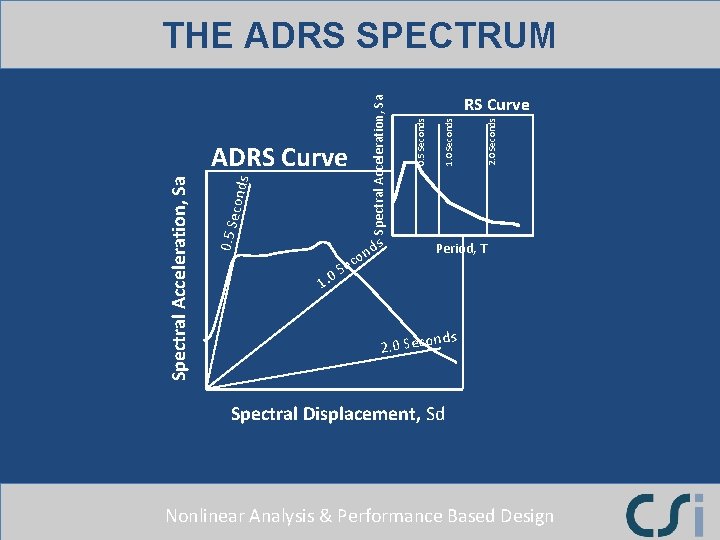
conds 0. 5 Se Spectral Acceleration, Sa s nd co 2. 0 Seconds 1. 0 Seconds RS Curve 0. 5 Seconds ADRS Curve Spectral Acceleration, Sa THE ADRS SPECTRUM Se 0 1. Period, T nds 2. 0 Seco Spectral Displacement, Sd Nonlinear Analysis & Performance Based Design

THE ADRS SPECTRUM Nonlinear Analysis & Performance Based Design
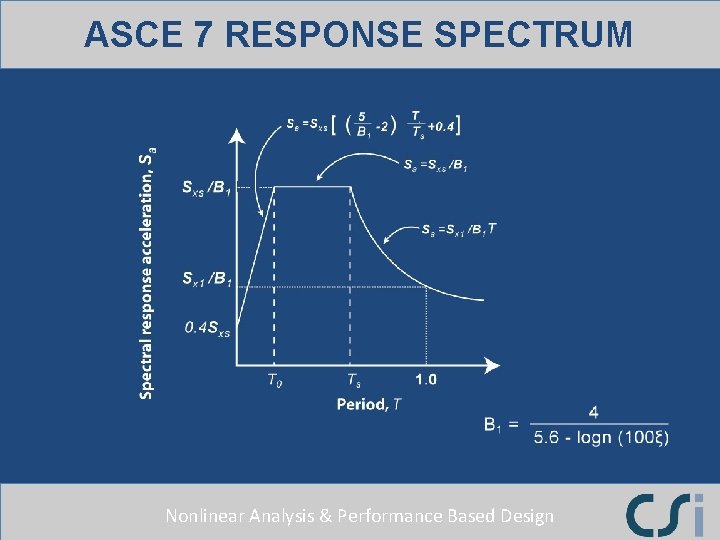
ASCE 7 RESPONSE SPECTRUM Nonlinear Analysis & Performance Based Design
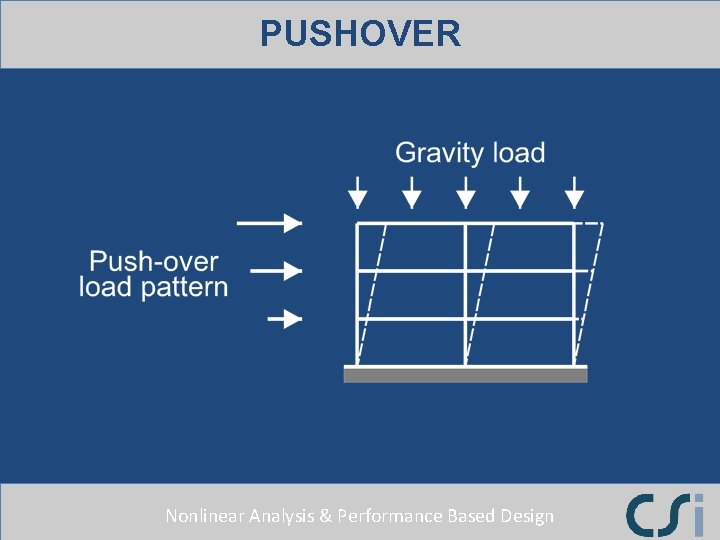
PUSHOVER Nonlinear Analysis & Performance Based Design
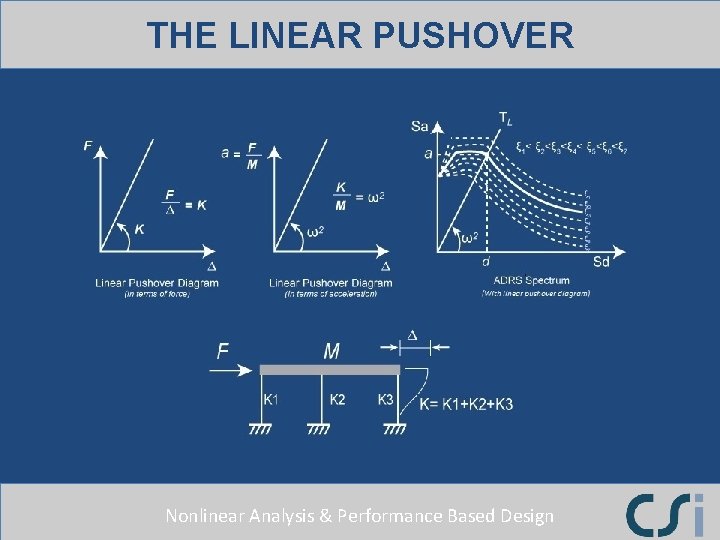
THE LINEAR PUSHOVER Nonlinear Analysis & Performance Based Design
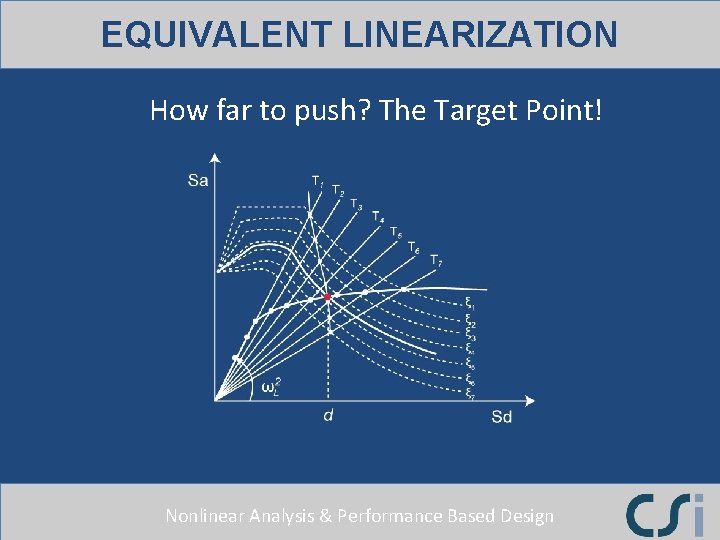
EQUIVALENT LINEARIZATION How far to push? The Target Point! Nonlinear Analysis & Performance Based Design
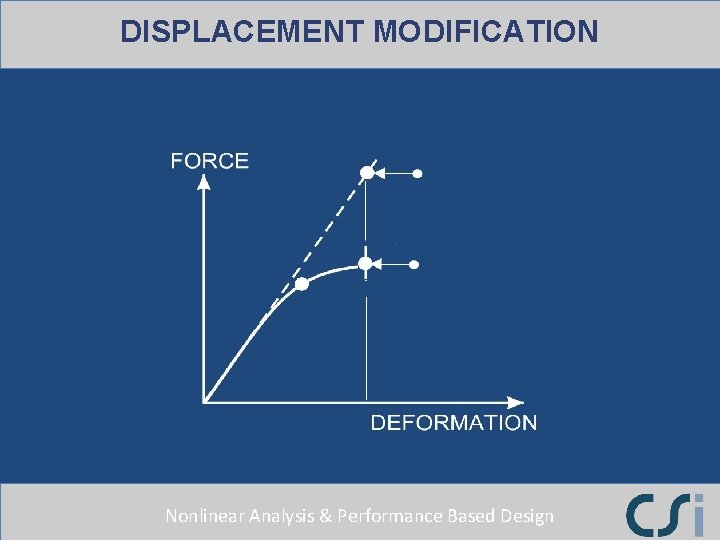
DISPLACEMENT MODIFICATION Nonlinear Analysis & Performance Based Design

DISPLACEMENT MODIFICATION Calculating the Target Displacement 2 2 d = C C C S T / (4 p ) 0 1 2 a e C 0 Relates spectral to roof displacement C 1 Modifier for inelastic displacement C 2 Modifier for hysteresis loop shape Nonlinear Analysis & Performance Based Design
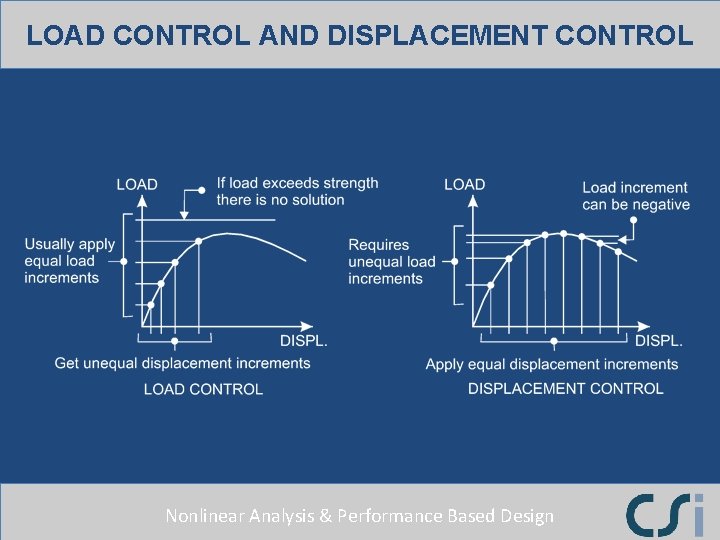
LOAD CONTROL AND DISPLACEMENT CONTROL Nonlinear Analysis & Performance Based Design

P-DELTA ANALYSIS Nonlinear Analysis & Performance Based Design
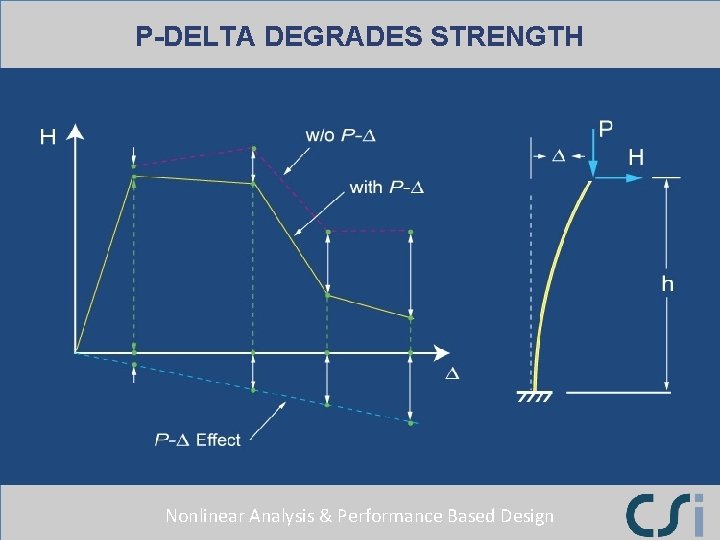
P-DELTA DEGRADES STRENGTH Nonlinear Analysis & Performance Based Design
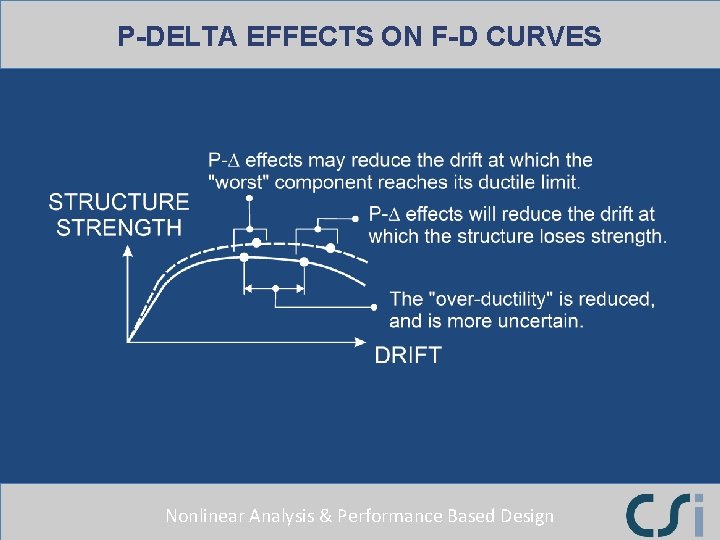
P-DELTA EFFECTS ON F-D CURVES Nonlinear Analysis & Performance Based Design

THE FAST NONLINEAR ANALYSIS METHOD (FNA) NON LINEAR FRAME AND SHEAR WALL HINGES BASE ISOLATORS (RUBBER & FRICTION) STRUCTURAL DAMPERS STRUCTURAL UPLIFT STRUCTURAL POUNDING BUCKLING RESTRAINED BRACES Nonlinear Analysis & Performance Based Design
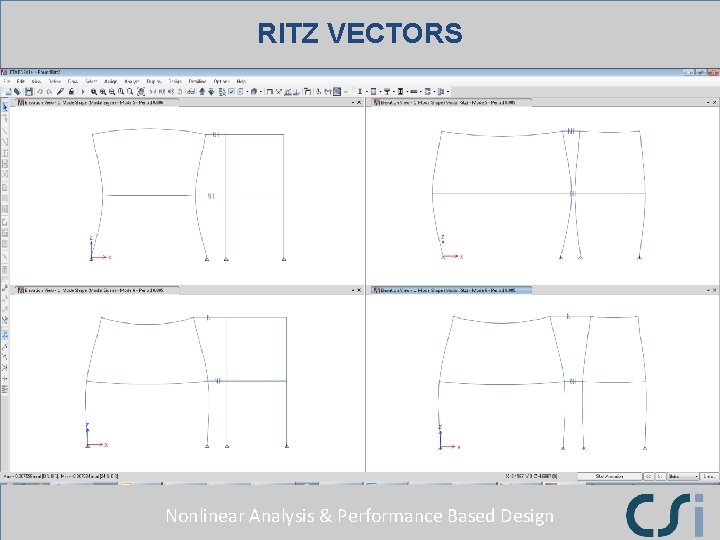
RITZ VECTORS Nonlinear Analysis & Performance Based Design

FNA KEY POINT The Ritz modes generated by the nonlinear deformation loads are used to modify the basic structural modes whenever the nonlinear elements go nonlinear. Nonlinear Analysis & Performance Based Design

ARTIFICIAL EARTHQUAKES CREATING HISTORIES TO MATCH A SPECTRUM FREQUENCY CONTENTS OF EARTHQUAKES FOURIER TRANSFORMS Nonlinear Analysis & Performance Based Design
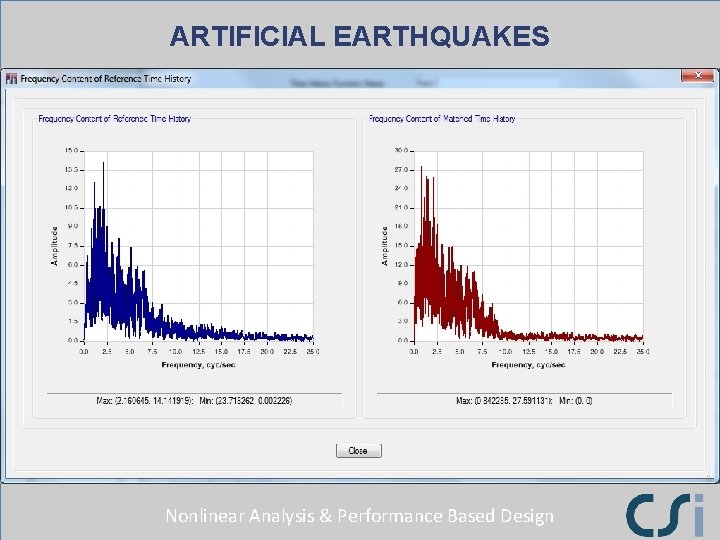
ARTIFICIAL EARTHQUAKES Nonlinear Analysis & Performance Based Design

MESH REFINEMENT 71 Nonlinear Analysis & Performance Based Design

APPROXIMATING BENDING BEHAVIOR This is for a coupling beam. A slender pier is similar. 72 Nonlinear Analysis & Performance Based Design

ACCURACY OF MESH REFINEMENT 73 Nonlinear Analysis & Performance Based Design
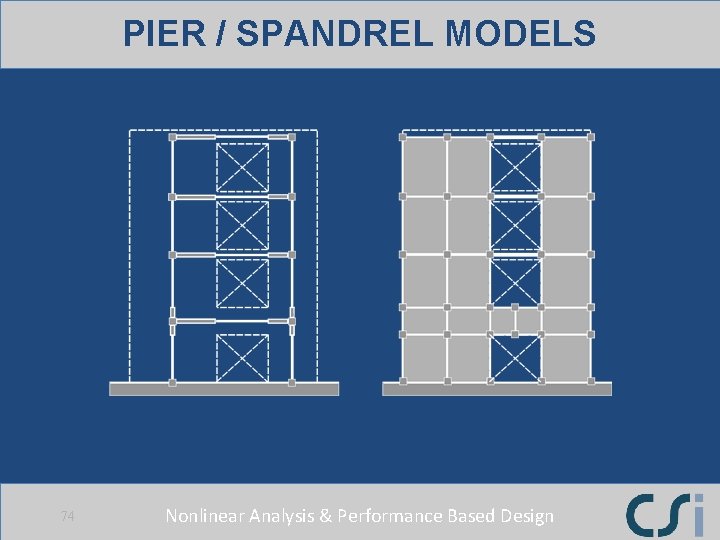
PIER / SPANDREL MODELS 74 Nonlinear Analysis & Performance Based Design
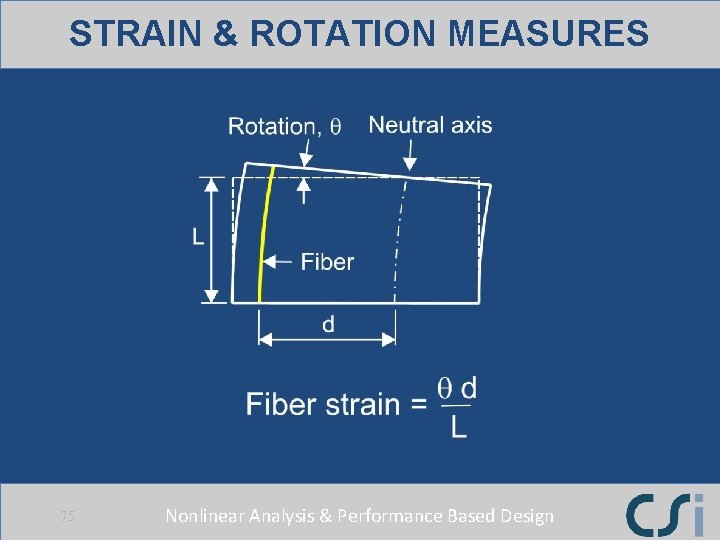
STRAIN & ROTATION MEASURES 75 Nonlinear Analysis & Performance Based Design

STRAIN CONCENTRATION STUDY Compare calculated strains and rotations for the 3 cases. 76 Nonlinear Analysis & Performance Based Design
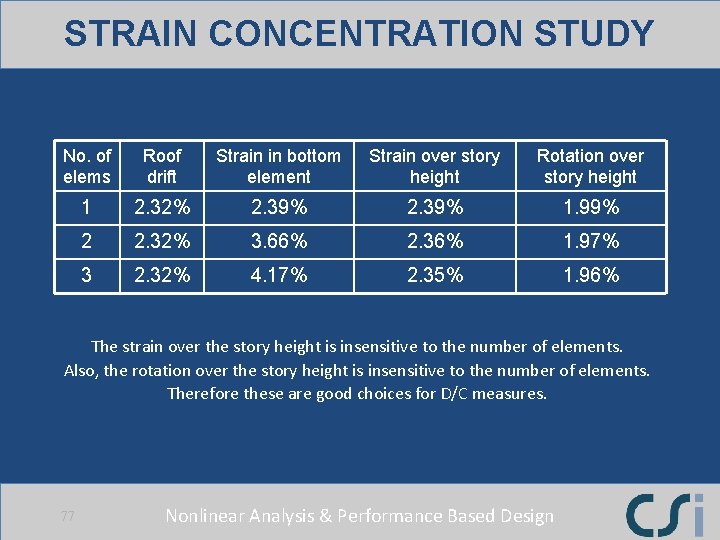
STRAIN CONCENTRATION STUDY No. of elems Roof drift Strain in bottom element Strain over story height Rotation over story height 1 2. 32% 2. 39% 1. 99% 2 2. 32% 3. 66% 2. 36% 1. 97% 3 2. 32% 4. 17% 2. 35% 1. 96% The strain over the story height is insensitive to the number of elements. Also, the rotation over the story height is insensitive to the number of elements. Therefore these are good choices for D/C measures. 77 Nonlinear Analysis & Performance Based Design
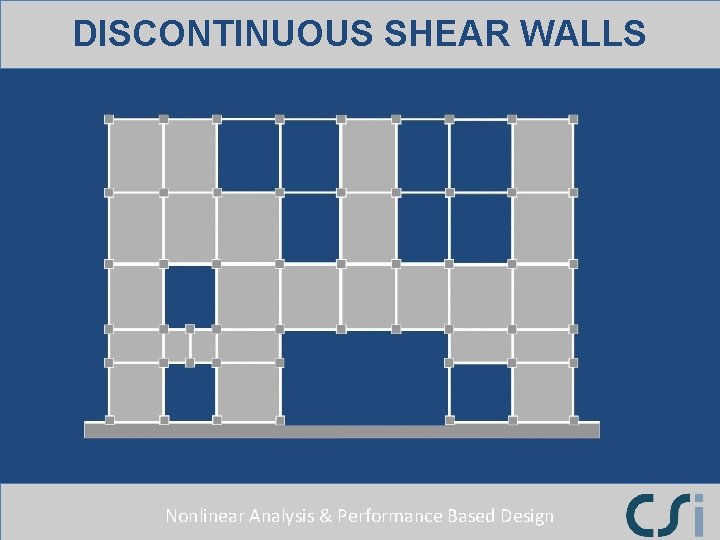
DISCONTINUOUS SHEAR WALLS Nonlinear Analysis & Performance Based Design
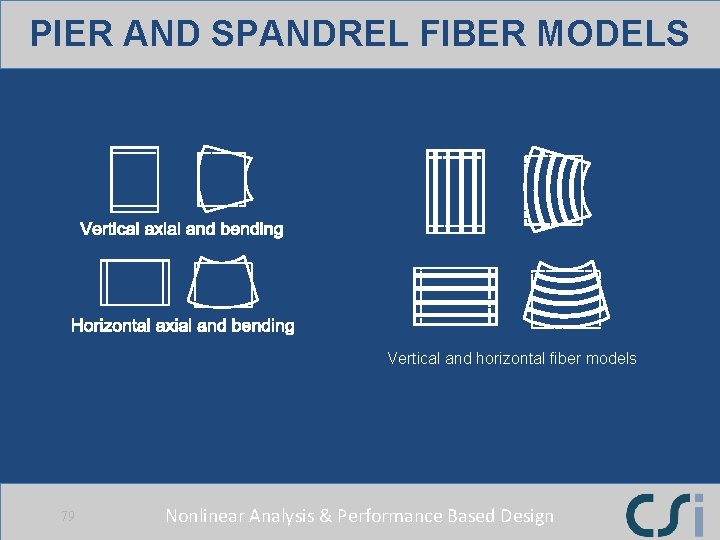
PIER AND SPANDREL FIBER MODELS Vertical and horizontal fiber models 79 Nonlinear Analysis & Performance Based Design

RAYLEIGH DAMPING • The a. M dampers connect the masses to the ground. They exert external damping forces. Units of a are 1/T. • The b. K dampers act in parallel with the elements. They exert internal damping forces. Units of b are T. • The damping matrix is C = a. M + b. K. Nonlinear Analysis & Performance Based Design 80
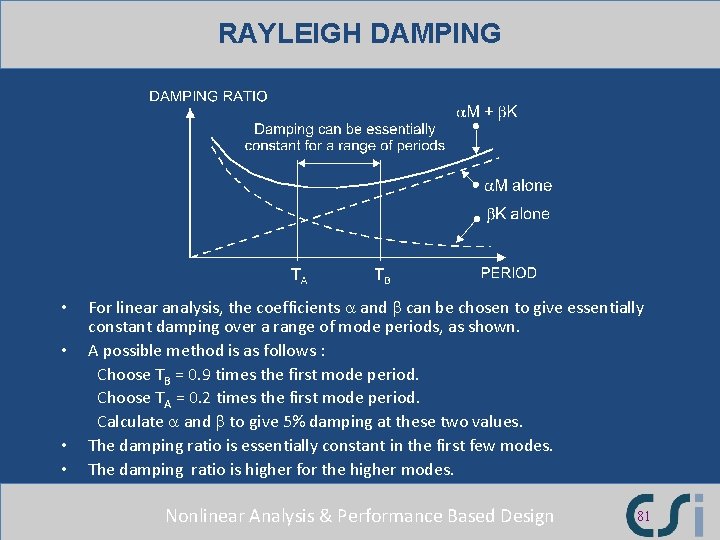
RAYLEIGH DAMPING • • For linear analysis, the coefficients a and b can be chosen to give essentially constant damping over a range of mode periods, as shown. A possible method is as follows : Choose TB = 0. 9 times the first mode period. Choose TA = 0. 2 times the first mode period. Calculate a and b to give 5% damping at these two values. The damping ratio is essentially constant in the first few modes. The damping ratio is higher for the higher modes. Nonlinear Analysis & Performance Based Design 81

RAYLEIGH DAMPING & = 0 + M& u& C u Ku + t M& u& & + + + u Ku = 0 K M ) ( a b t & u& + C u&+ M K u M = 0 2 & u& + 2 x wu& + w u = 0 ; 2 x M w = C x= C 2 Mw = C 2 M K M = C 2 KM = a. M + b. K 2 KM x = 2 aw + b w 2 Nonlinear Analysis & Performance Based Design 2 KM

RAYLEIGH DAMPING Higher Modes (high w) = b Lower Modes (low w) = a K To get z from a & b for w = M ; T = 2 p w any To get a & b from two values of z 1& z 2 z 1 = a + b w 1 2 2 w 1 z 2 = a + b w 2 2 2 w Solve for a & b 2 Nonlinear Analysis & Performance Based Design
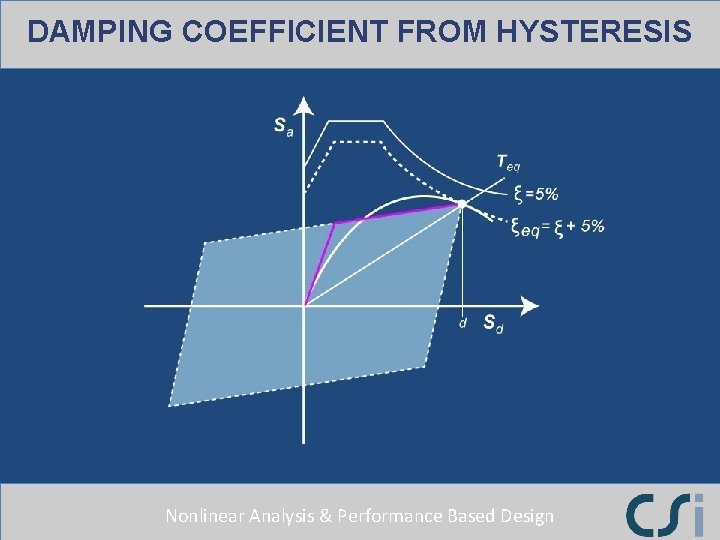
DAMPING COEFFICIENT FROM HYSTERESIS Nonlinear Analysis & Performance Based Design

DAMPING COEFFICIENT FROM HYSTERESIS Nonlinear Analysis & Performance Based Design

A BIG THANK YOU!!! Nonlinear Analysis & Performance Based Design
- Slides: 86