NonExperimental designs Correlational Quasiexperimental designs Psych 231 Research













- Slides: 20

Non-Experimental designs: Correlational & Quasi-experimental designs Psych 231: Research Methods in Psychology

n Sometimes you just can’t perform a fully controlled experiment n n Because of the issue of interest Limited resources (not enough subjects, observations are too costly, etc). • • • n Surveys Correlational Quasi-Experiments Developmental designs Small-N designs This does NOT imply that they are bad designs n Just remember the advantages and disadvantages of each Non-Experimental designs

n Looking for a co-occurrence relationship between two (or more) variables n Used for • Descriptive research • do behaviors co-occur? • Predictive research • is one behavior predictive of another? • Reliability and Validity • Does your measure correlate with others (and itself)? • Evaluating theories • Look for co-occurrence posited by theory. Correlational designs

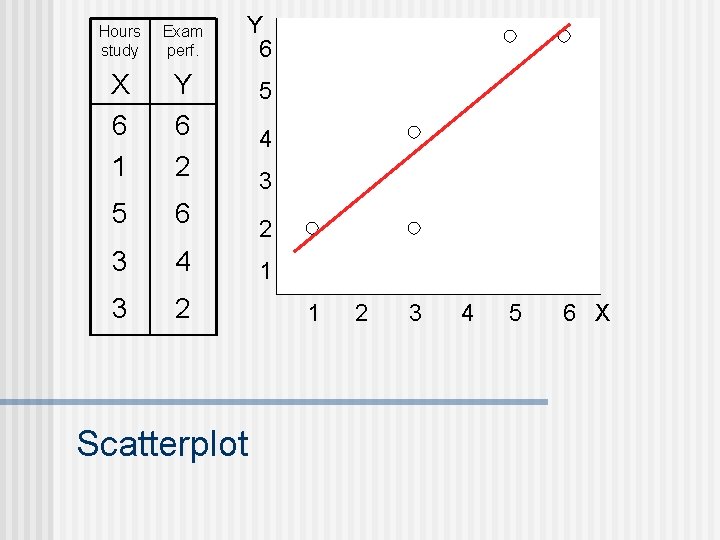
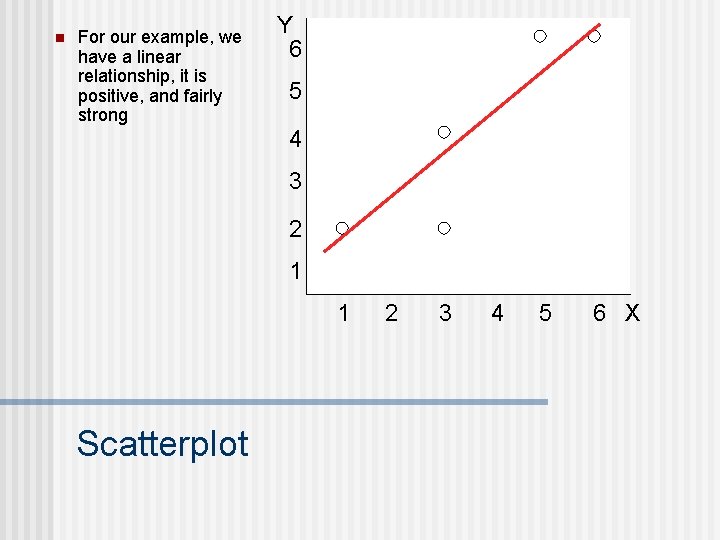
n Looking for a co-occurrence relationship between two (or more) variables n Example 1: Suppose that you notice that the more you study for an exam, the better your score typically is. n n This suggests that there is a relationship between study time and test performance. We call this relationship a correlation. n 3 properties: form, direction, strength Correlational designs

Hours study Exam perf. X 6 1 Y 6 2 5 6 3 4 3 2 Y 6 Scatterplot 5 4 3 2 1 1 2 3 4 5 6 X

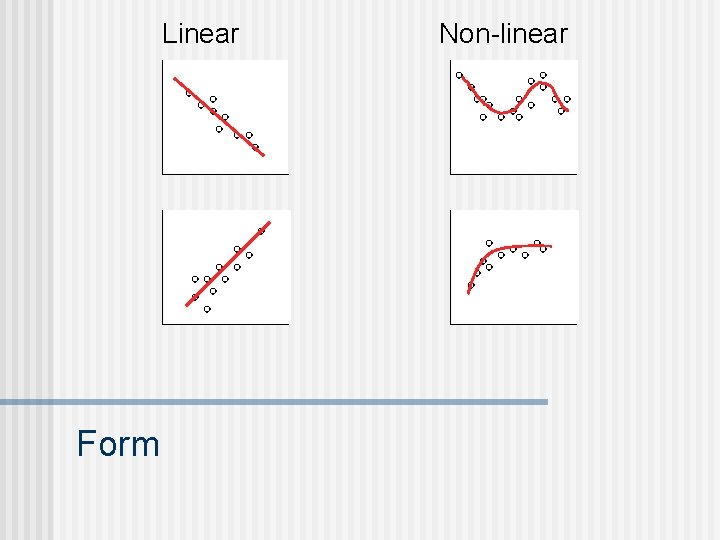
Linear Form Non-linear

Positive Negative Y • X & Y vary in the same direction Direction Y X • X & Y vary in opposite directions X

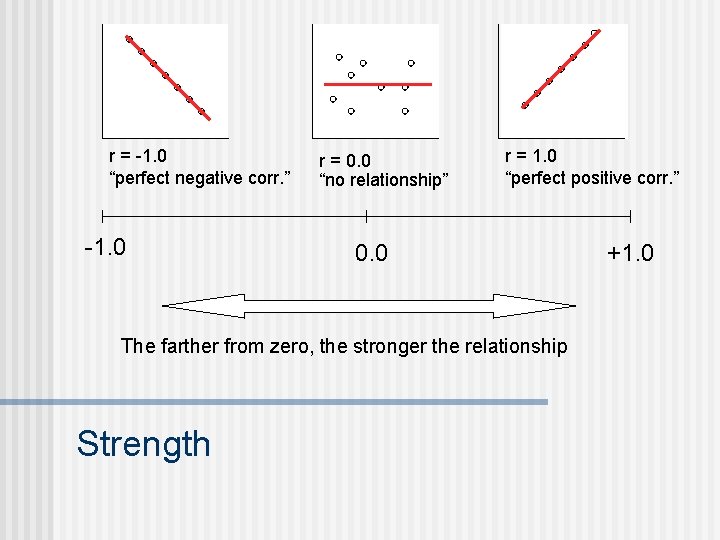
r = -1. 0 “perfect negative corr. ” -1. 0 r = 0. 0 “no relationship” r = 1. 0 “perfect positive corr. ” 0. 0 The farther from zero, the stronger the relationship Strength +1. 0

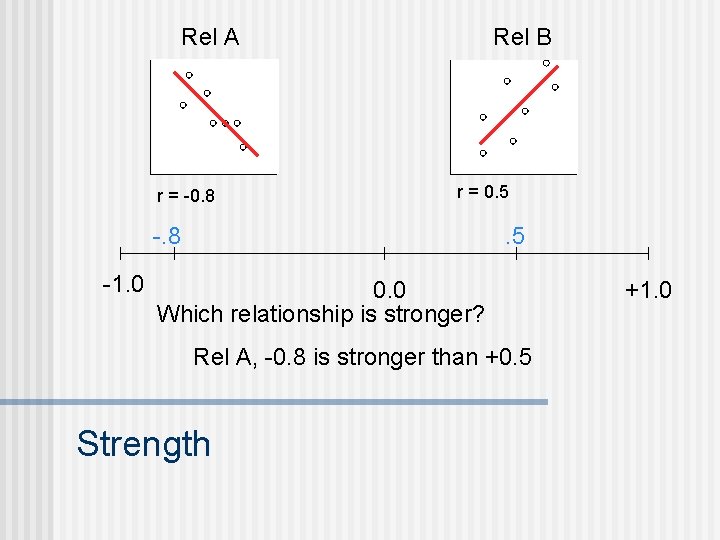
Rel A r = -0. 8 Rel B r = 0. 5 -. 8 -1. 0 . 5 0. 0 Which relationship is stronger? Rel A, -0. 8 is stronger than +0. 5 Strength +1. 0

n For our example, we have a linear relationship, it is positive, and fairly strong Y 6 5 4 3 2 1 1 Scatterplot 2 3 4 5 6 X

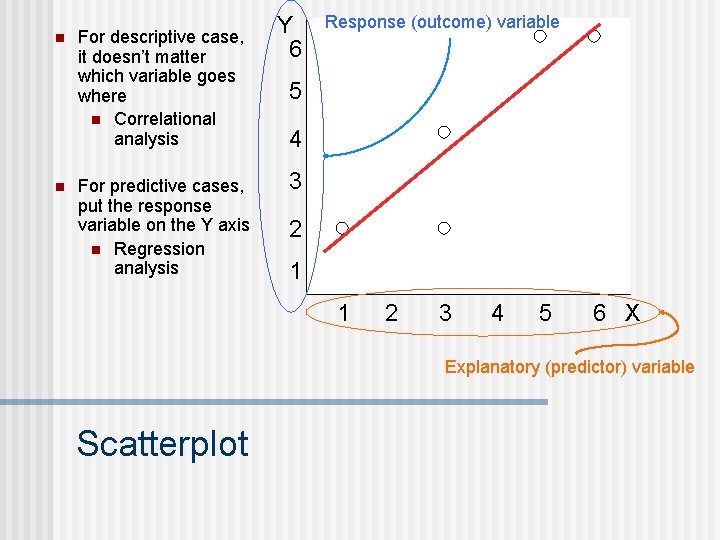
n Looking for a co-occurrence relationship between two (or more) variables n n n Explanatory variables (Predictor variables) Response variables (Outcome variables) Example 1: Suppose that you notice that the more you study for an exam, the better your score typically is n For our example, which variable is explanatory and which is response? And why? n It depends on your theory of the causal relationship between the variables Correlational designs

n n For descriptive case, it doesn’t matter which variable goes where n Correlational analysis For predictive cases, put the response variable on the Y axis n Regression analysis Y 6 Response (outcome) variable 5 4 3 2 1 1 2 3 4 5 6 X Explanatory (predictor) variable Scatterplot

n Advantages: n Doesn’t require manipulation of variable • Sometimes the variables of interest can’t be manipulated n n Allows for simple observations of variables in naturalistic settings (increasing external validity) Can look at a lot of variables at once Correlational designs

n Disadvantages: n Don’t make casual claims • Third variable problem • Temporal precedence • Coincidence (random co-occurence) n Correlational results are often misinterpreted Correlational designs

n Disadvantages: n Example 2: Suppose that you notice that kids who sit in the front of class typically get higher grades. n This suggests that there is a relationship between where you sit in class and grades. Daily Gazzett Children who sit in the back of the classroom receive lower grades than those who sit in the front. Possibly implied: “[All] Children who sit in the back of the classroom [always] receive worse grades than [each and every child] who sits in the front. ” Better: “Researchers X and Y found that children who sat in the back of the classroom were more likely to receive lower grades than those who sat in the front. ” Misunderstood Correlational designs Example from Owen Emlen (2006)

What are they? n n n Almost “true” experiments, but with an inherent confounding variable General types 1) An event occurs that the experimenter doesn’t manipulate • Something not under the experimenter’s control • (e. g. , flashbulb memories for traumatic events) 2) Interested in subject variables – high vs. low IQ, males vs. females 3) Time is used as a variable Quasi-experiments

n Advantages n n n Allows applied research when experiments not possible Threats to internal validity can be assessed (sometimes) Disadvantages n n n Threats to internal validity may exist Designs are more complex than traditional experiments Statistical analysis can be difficult • Most statistical analyses assume randomness Quasi-experiments

Program evaluation n – Research on programs that is implemented to achieve some positive effect on a group of individuals. – – e. g. , does abstinence from sex program work in schools Steps in program evaluation – – – Needs assessment - is there a problem? Program theory assessment - does program address the needs? Process evaluation - does it reach the target population? Is it being run correctly? Outcome evaluation - are the intended outcomes being realized? Efficiency assessment- was it “worth” it? The the benefits worth the costs? Quasi-experiments

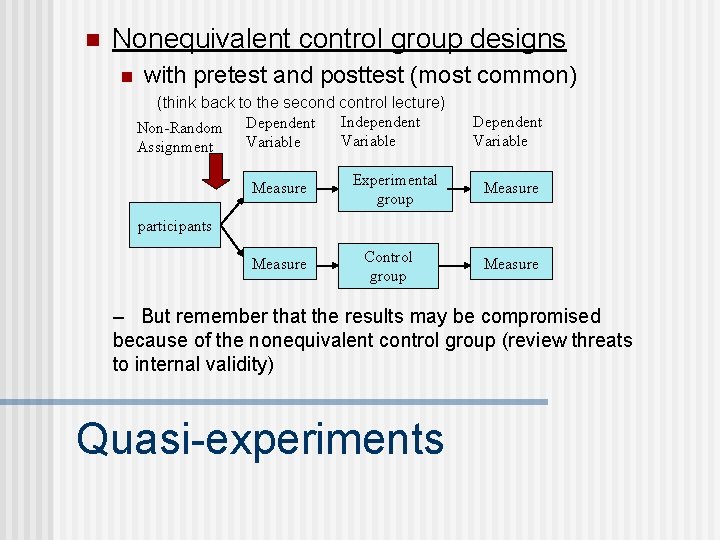
n Nonequivalent control group designs n with pretest and posttest (most common) (think back to the second control lecture) Independent Non-Random Dependent Variable Assignment Measure Experimental group Dependent Variable Measure participants Measure Control group Measure – But remember that the results may be compromised because of the nonequivalent control group (review threats to internal validity) Quasi-experiments

n Interrupted & Non-interrupted time series designs n Observe a single group multiple times prior to and after a treatment Obs Obs Treatment Obs Obs • Look for an instantaneous, permanent change • Interrupted – when treatment was not introduced by researcher, for example some historical event n Variations of basic time series design • Addition of a nonequivalent no-treatment control group time series OOOTOOO & OOO_OOO • Interrupted time series with removed treatment • If treatment effect is reversible Quasi-experiments