NONEUCLIDEAN GEOMETRY Compiled Still John F Reyes INTRODUCTION

NON-EUCLIDEAN GEOMETRY Compiled: Still John F. Reyes

INTRODUCTION TO NON-EUCLIDEAN GEOMETRY • Non-Euclidean geometry differs from the geometry of Euclid because it substitutes another alternative for his so-called fifth postulate. • The fifth postulate as stated by Euclid: “If a transversal falls on two lines in such a way that the interior angles on one side of the transversal are less than two right angles, then the lines meet on that side on which the angles are less than two right angles. ”

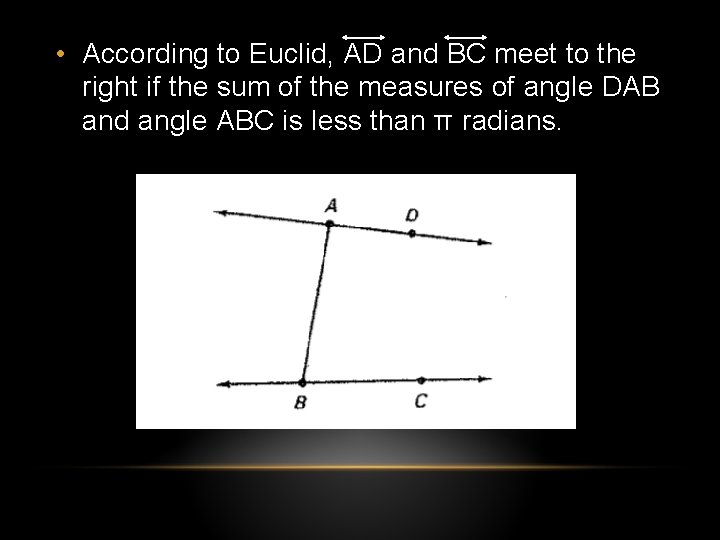
• According to Euclid, AD and BC meet to the right if the sum of the measures of angle DAB and angle ABC is less than π radians.

• Note that the word “parallel” does not appear in the fifth postulate. • The wording of Euclid’s fifth postulate that is most commonly used is called Playfair’s axiom: Through a point not on a given line, exactly one line can be drawn in the plane parallel to the given line. • The word “parallel” means not intersecting or having no Euclidean point in common. • Playfair’s axiom and the original fifth postulate are logically equivalent.

• From the time Euclid stated his postulates, about 300 B. C. , mathematicians attempted to show that the fifth postulate was actually a theorem that could be proved from the other postulates. None of these people succeeded. • Shortly after 1800, mathematicians such as Carl Friedrich Gauss began to realize that the fifth postulate could never be proved from the others, because it was indeed an independent postulate in the set of Euclidean postulates, not a theorem.

• The first account of non-Euclidean geometry to be published was based on the assumption that, through a point not on a given line, more than one line can be drawn parallel to a given line in the plane. • This type of geometry, called hyperbolic geometry, was discovered independently by a Russian, Nikolai Lobachevsky (1793 -1856), and, at about the same time, by a Hungarian, Janos Bolyai (1802 -1860).

• The results were published about 1830. • A second type of non-Euclidean geometry, elliptic geometry, is introduced briefly.

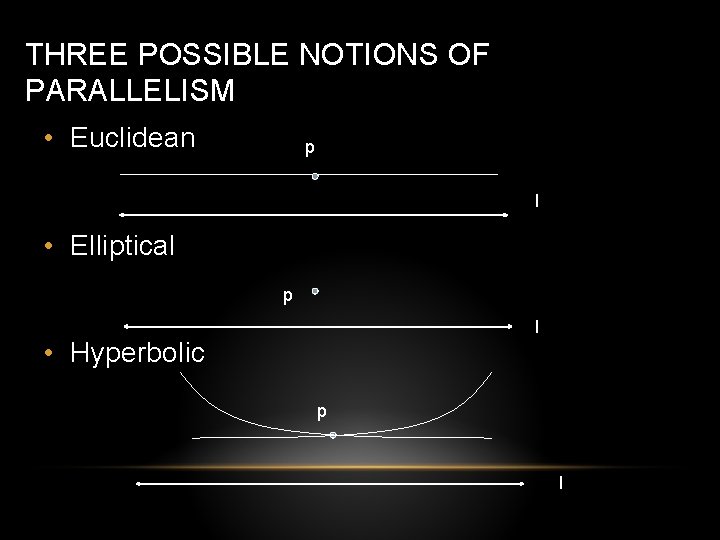
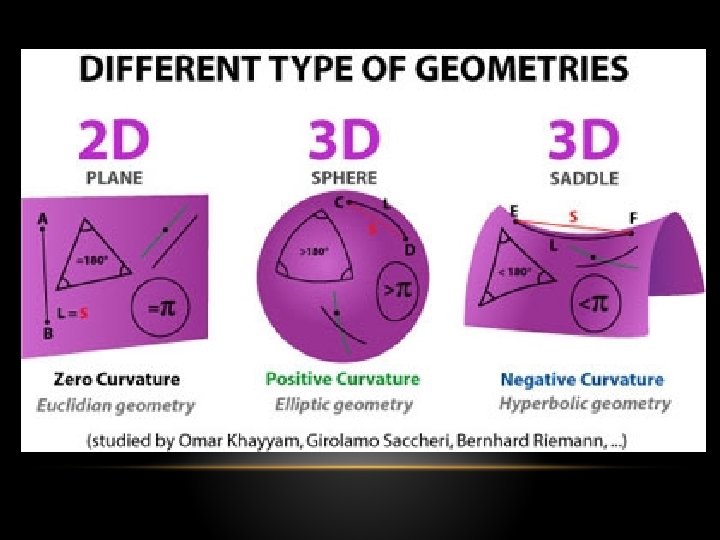
THREE POSSIBLE NOTIONS OF PARALLELISM • Euclidean: given a line l and point p, there is exactly one line parallel to l through p • Elliptical/Spherical: given a line l and point p, there is no line parallel to l through p • Hyperbolic: given a line l and point p, there are infinite lines parallel to l through p

THREE POSSIBLE NOTIONS OF PARALLELISM • Euclidean p l • Elliptical p l • Hyperbolic p l

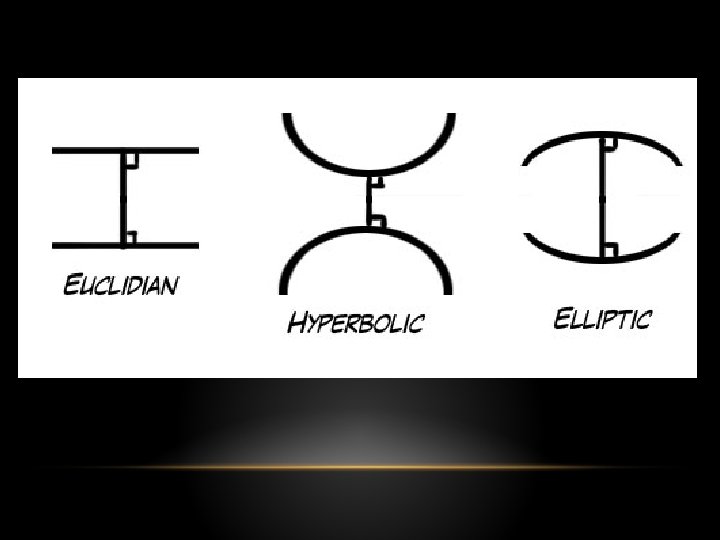
EUCLIDEAN & NON-EUCLIDEAN GEOMETRY • Euclidean: the lines remain at a constant distance from each other and are parallels • Hyperbolic: the lines “curve away” from each other and increase in distance as one moves further from the points of intersection but with a common perpendicular and are ultraparallels • Elliptic: the lines “curve toward” each other and eventually intersect with each other

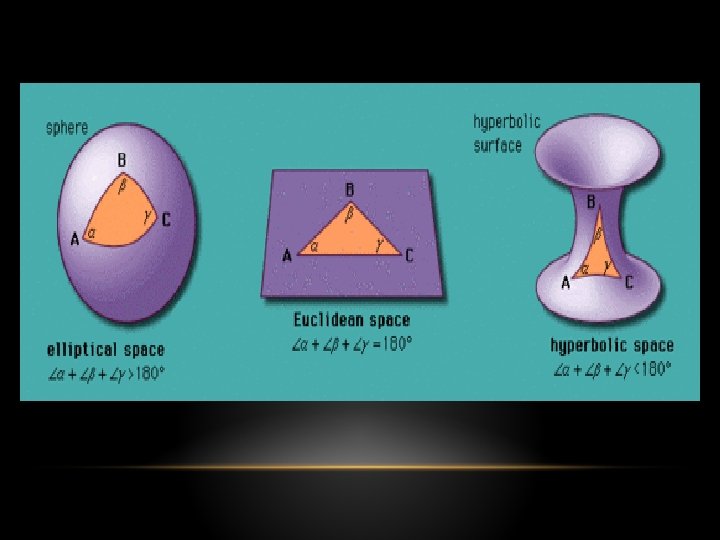
EUCLIDEAN & NON-EUCLIDEAN GEOMETRY • Euclidean: the sum of the angles of any triangle is always equal to 180° • Hyperbolic: the sum of the angles of any triangle is always less than 180° • Elliptic: the sum of the angles of any triangle is always greater than 180°; geometry in a sphere with great circles

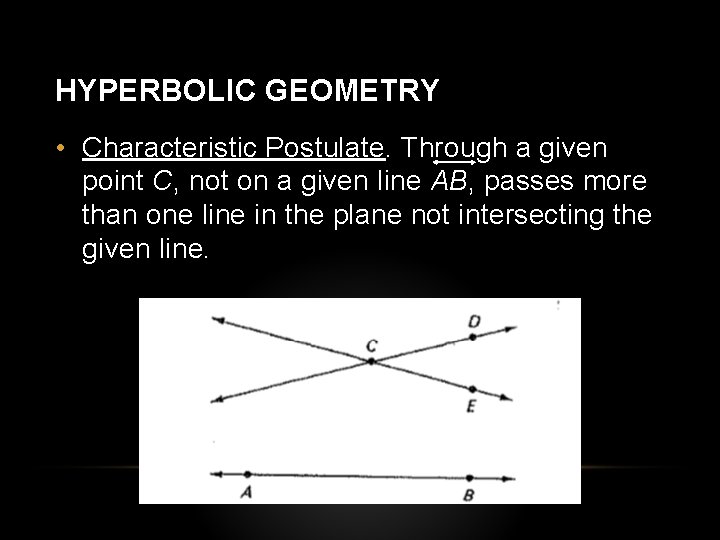
HYPERBOLIC GEOMETRY • Characteristic Postulate. Through a given point C, not on a given line AB, passes more than one line in the plane not intersecting the given line.

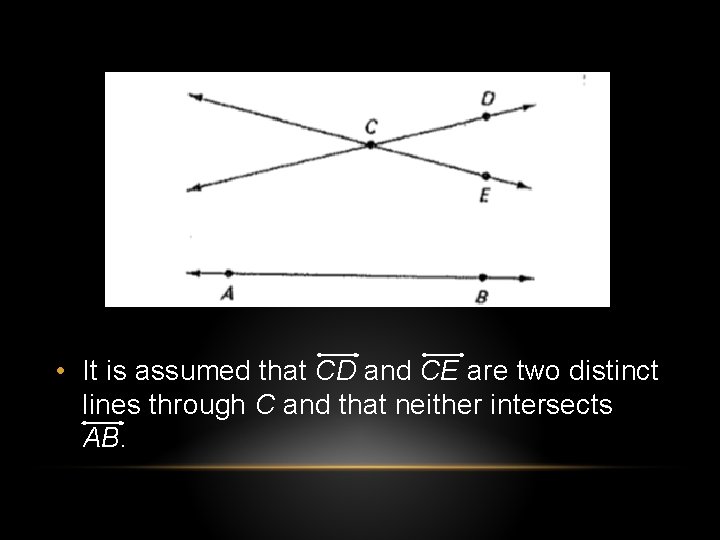
• It is assumed that CD and CE are two distinct lines through C and that neither intersects AB.

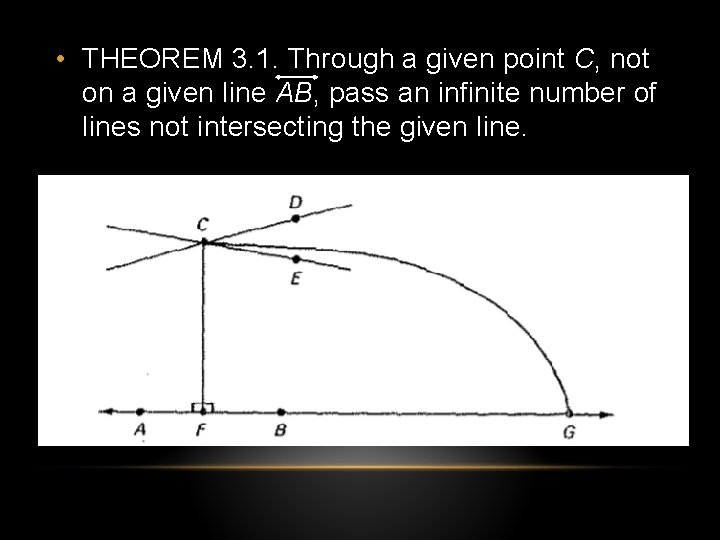
• THEOREM 3. 1. Through a given point C, not on a given line AB, pass an infinite number of lines not intersecting the given line.

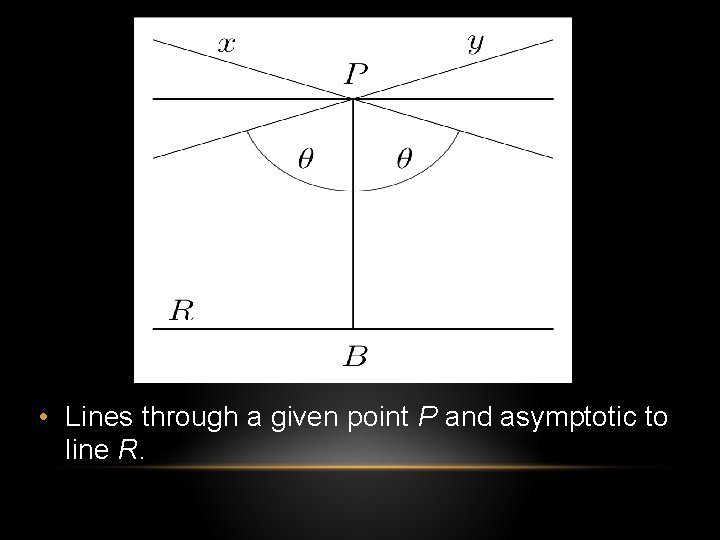
• Lines through a given point P and asymptotic to line R.

ELLIPTIC GEOMETRY • German mathematician Bernhard Riemann (1826 -1866) suggested a geometry, now called elliptic, based on the alternative to the fifth postulate, which states that there are no parallels to a line through a point on the line. • Characteristic Postulate of Elliptic Geometry. Any two lines in a plane meet at an ordinary point.

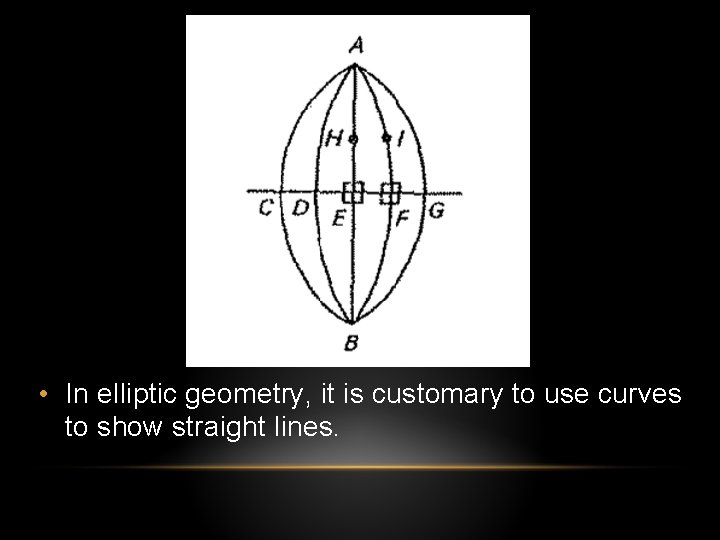
• If the figure is in elliptic geometry, with EH and FI both perpendicular to CG, these two lines meet at some point A because of the characteristic postulate that any two lines intersect.

• In elliptic geometry, it is customary to use curves to show straight lines.

• One type of geometry that could overlap with elliptic geometry is called spherical geometry. • In spherical geometry, there are no parallel lines since any two lines must intersect. • However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point (rather than two) in elliptic geometry. • Because of this, the elliptic geometry is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.

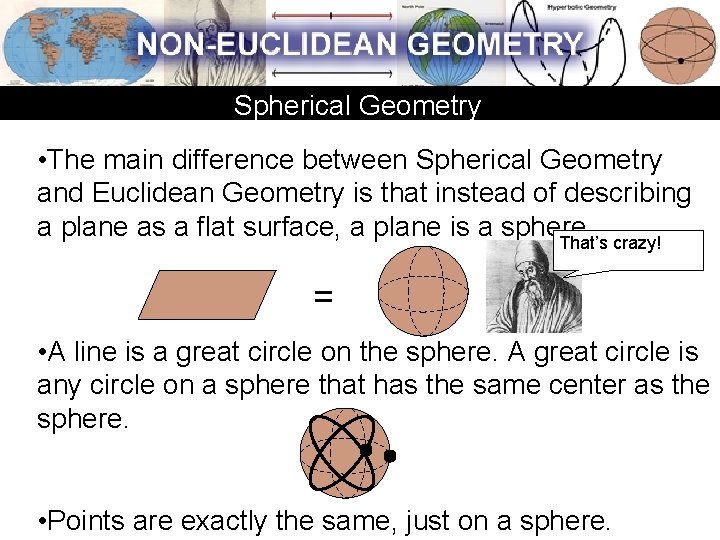
Spherical Geometry • The main difference between Spherical Geometry and Euclidean Geometry is that instead of describing a plane as a flat surface, a plane is a sphere. That’s crazy! = • A line is a great circle on the sphere. A great circle is any circle on a sphere that has the same center as the sphere. • Points are exactly the same, just on a sphere.

Spherical Geometry • Are Euclid’s Postulates true in Spherical Geometry? 1. Through any two points there is exactly one line TRUE Of course They’re true! 2. Through any three points not on the same line there is exactly one plane TRUE

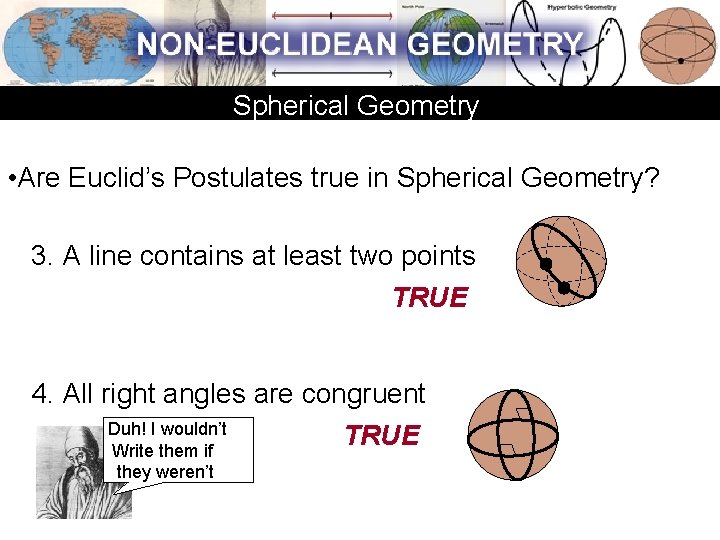
Spherical Geometry • Are Euclid’s Postulates true in Spherical Geometry? 3. A line contains at least two points TRUE 4. All right angles are congruent Duh! I wouldn’t TRUE Write them if they weren’t

Spherical Geometry • Is the Parallel Postulate true in Spherical Geometry? 5. Given a line and a point not on that line how many lines can be drawn through the point that are parallel to the line? NONE, Therefore the Parallel Postulate is FALSE in Spherical Geometry What the…!? That’s just weird

Spherical Geometry • Is the Parallel Postulate true in Spherical Geometry? 5. Given a line and a point not on that line how many lines can be drawn through the point that are parallel to the line? NONE, Therefore the Parallel Postulate is FALSE in Spherical Geometry Common Mistake: Except for the circle in the middle, these horizontal circles do not share a center with the sphere and are therefore can not be considered parallel lines, even though they appear to be parallel.

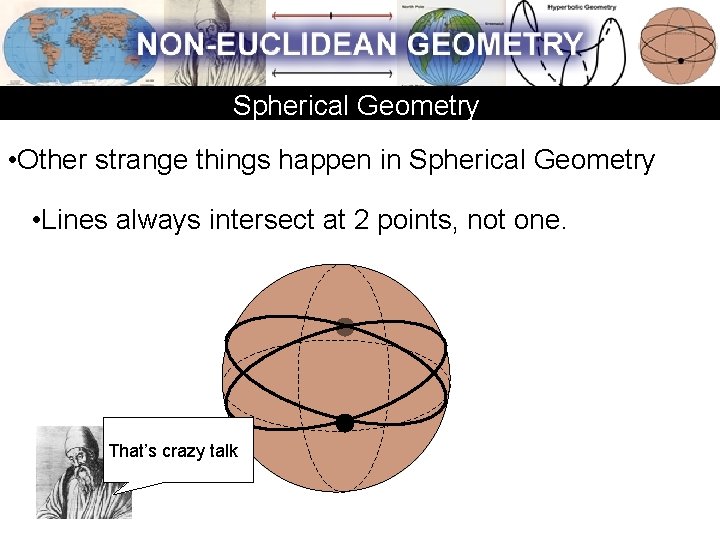
Spherical Geometry • Other strange things happen in Spherical Geometry • Lines always intersect at 2 points, not one. That’s crazy talk

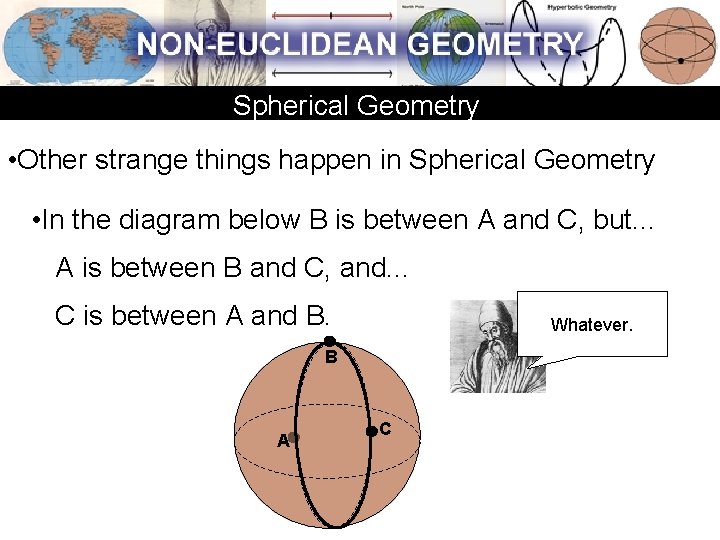
Spherical Geometry • Other strange things happen in Spherical Geometry • In the diagram below B is between A and C, but. . . A is between B and C, and. . . C is between A and B. Whatever. B A C

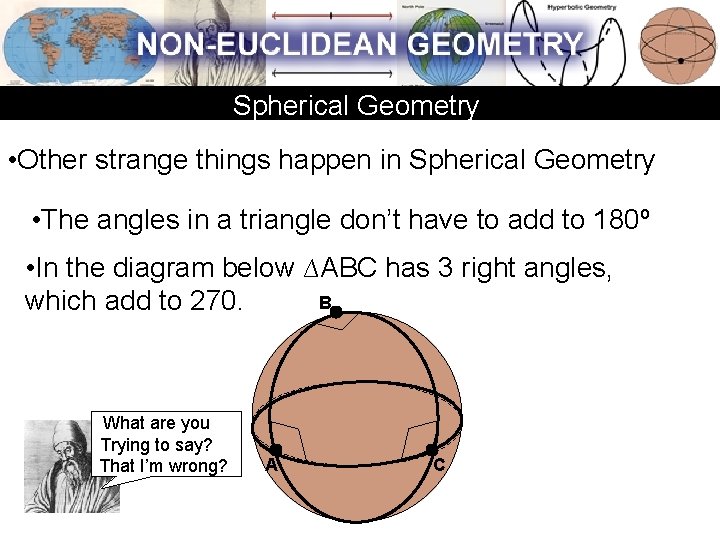
Spherical Geometry • Other strange things happen in Spherical Geometry • The angles in a triangle don’t have to add to 180º • In the diagram below ∆ABC has 3 right angles, B which add to 270. What are you Trying to say? That I’m wrong? A C

Spherical Geometry: A Real World Application • If Spherical Geometry is so strange why do we even bother studying it? Because the Earth is a Sphere. No It’s Flat. • Euclidean geometry cannot be used to model the Earth because it is a sphere. • Instead of the Cartesian coordinates used in Euclidean Geometry Longitude and Latitude are used as to define position of points on the Earth.

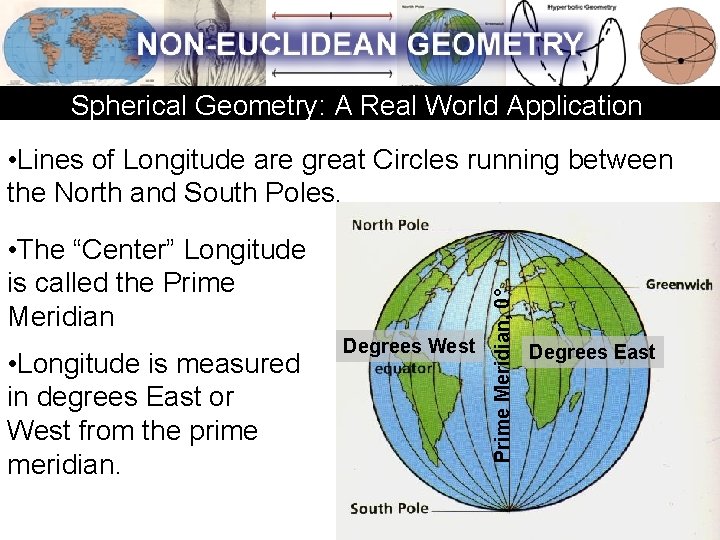
Spherical Geometry: A Real World Application • The “Center” Longitude is called the Prime Meridian • Longitude is measured in degrees East or West from the prime meridian. Degrees West Prime Meridian, 0° • Lines of Longitude are great Circles running between the North and South Poles. Degrees East

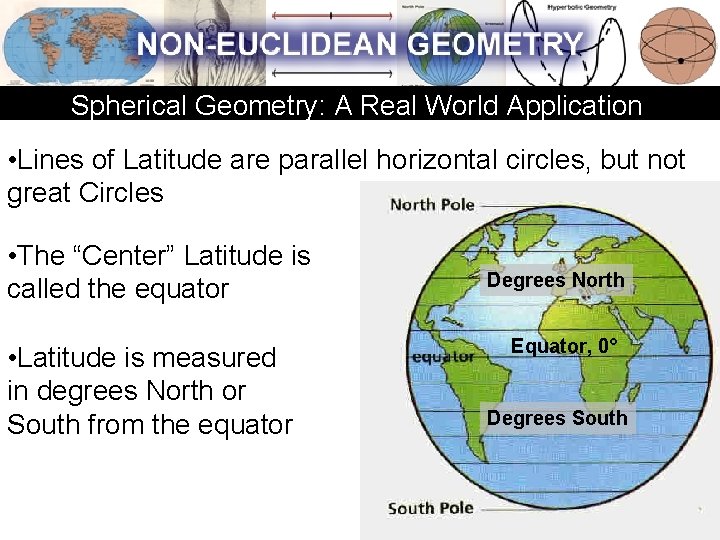
Spherical Geometry: A Real World Application • Lines of Latitude are parallel horizontal circles, but not great Circles • The “Center” Latitude is called the equator • Latitude is measured in degrees North or South from the equator Degrees North Equator, 0° Degrees South

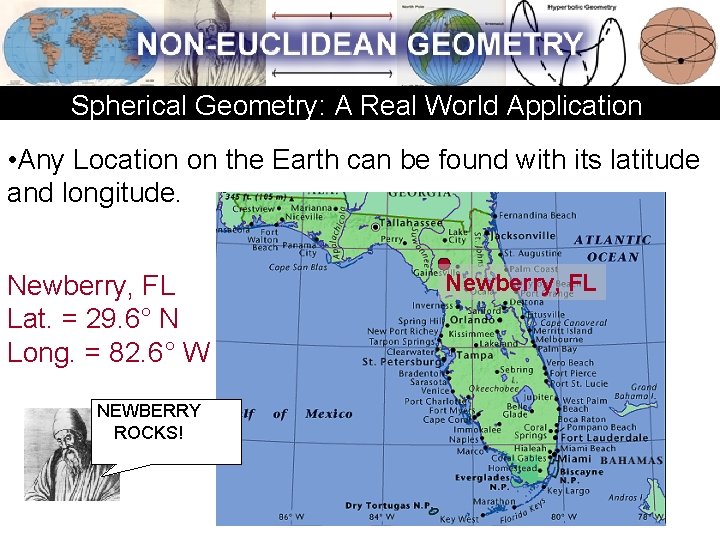
Spherical Geometry: A Real World Application • Any Location on the Earth can be found with its latitude and longitude. Newberry, FL Lat. = 29. 6° N Long. = 82. 6° W NEWBERRY ROCKS! Newberry, FL

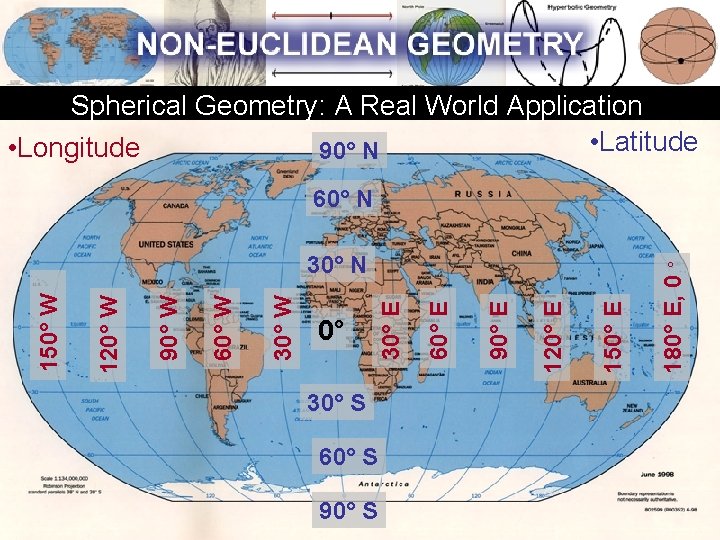
Spherical Geometry: A Real World Application • Latitude • Longitude 90° N 30° S 60° S 90° S 150° E 120° E 90° E 60° E 0° 30° E 30° W 60° W 90° W 120° W 150° W 30° N 180° E, 0 ° 60° N

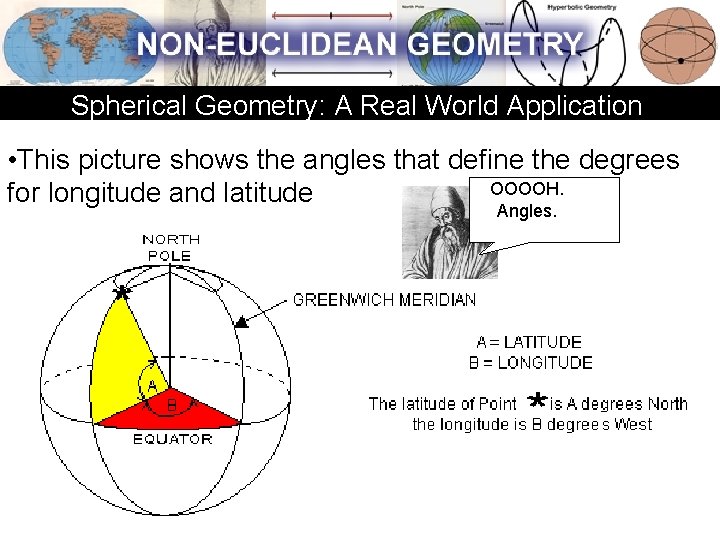
Spherical Geometry: A Real World Application • This picture shows the angles that define the degrees OOOOH. for longitude and latitude Angles.

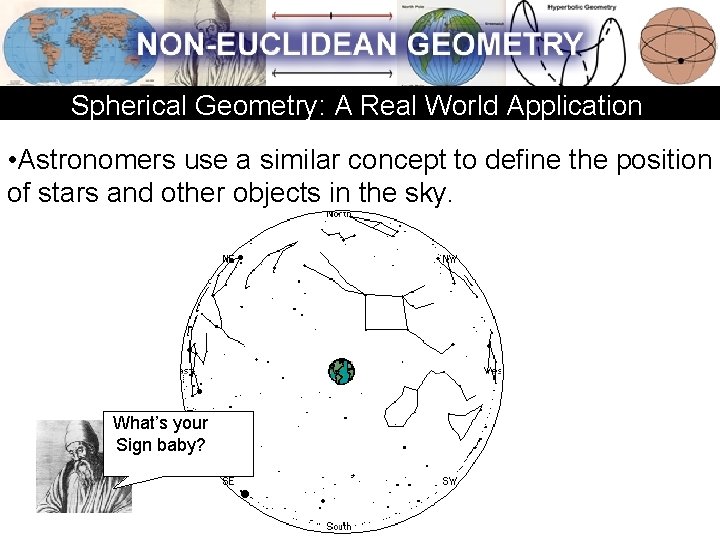
Spherical Geometry: A Real World Application • Astronomers use a similar concept to define the position of stars and other objects in the sky. What’s your Sign baby?

DO WORKSHEET 6