Nonequilibrium dynamics in the Dicke model Izabella Lovas

Non-equilibrium dynamics in the Dicke model Izabella Lovas Supervisor: Balázs Dóra Budapest University of Technology and Economics 2012. 11. 07.

Outline • Rabi model • Jaynes-Cummings model • Dicke model • Thermodynamic limit • Quantum phase transition • Normal and super-radiant phase • Experimental realization • General formula for the characteristic function of work • Special cases -Sudden quench -Linear quench

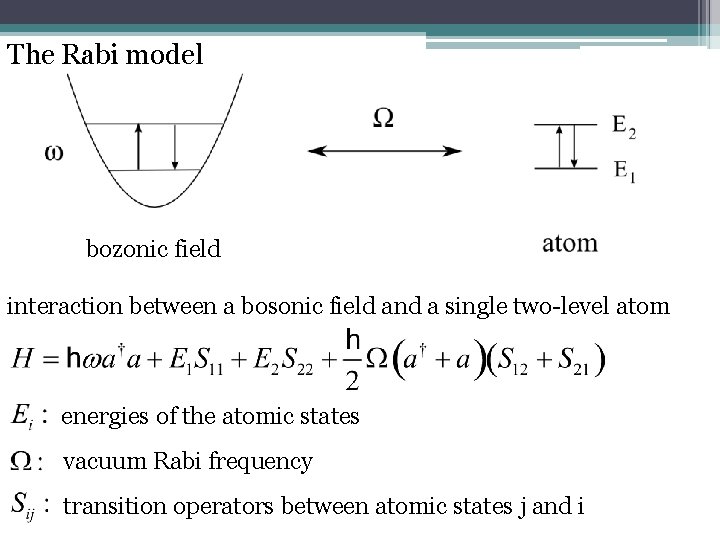
The Rabi model f field bozonic interaction between a bosonic field and a single two-level atom energies of the atomic states vacuum Rabi frequency transition operators between atomic states j and i

The Jaynes-Cummings model rotating-wave approximation: are neglected conservation of excitation: is exactly solvable: infinite set of uncoupled two-state Schrödinger equations for n excitations: basis states if the initial state is a basis state, we get sinusoidal changes in populations: Rabi oscillations

The Dicke model bosonic field N atoms generalization of the Rabi model: N atoms, single mode field collective atomic operators -level system pseudospin vector of length

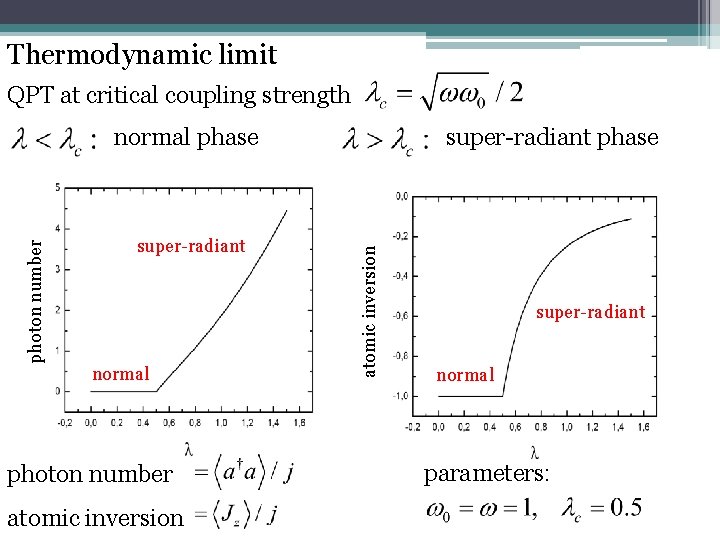
Thermodynamic limit QPT at critical coupling strength super-radiant normal photon number atomic inversion super-radiant phase atomic inversion photon number normal phase super-radiant normal parameters:

Thermodynamic limit Holstein-Primakoff representation: Normal phase: two coupled harmonic oscillators real parity operator: ground state has positive parity

Super-radiant phase macroscopic occupation of the field and the atomic ensemble or linear terms in the Hamiltonian disappear where mean photon number: global symmetry becomes broken new local symmetries:

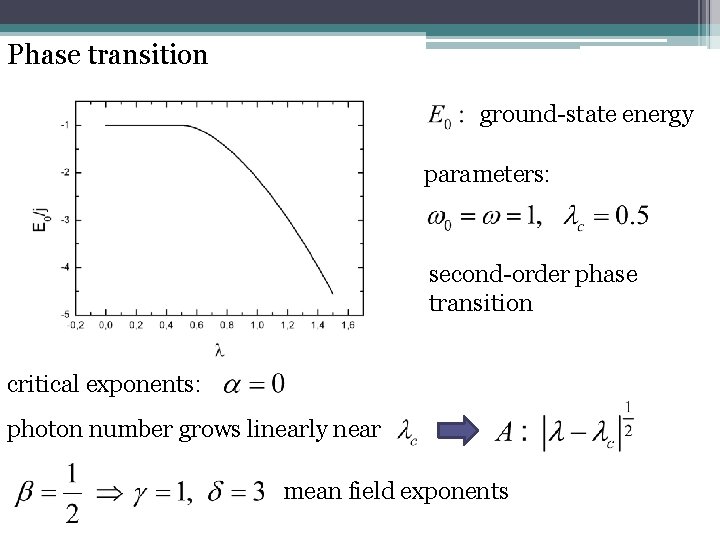
Phase transition ground-state energy parameters: second-order phase transition critical exponents: photon number grows linearly near mean field exponents

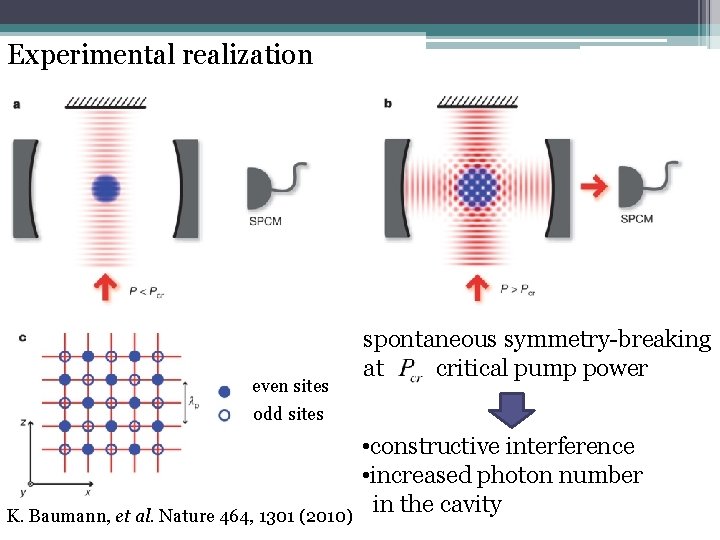
Experimental realization even sites spontaneous symmetry-breaking at critical pump power odd sites K. Baumann, et al. Nature 464, 1301 (2010) • constructive interference • increased photon number in the cavity

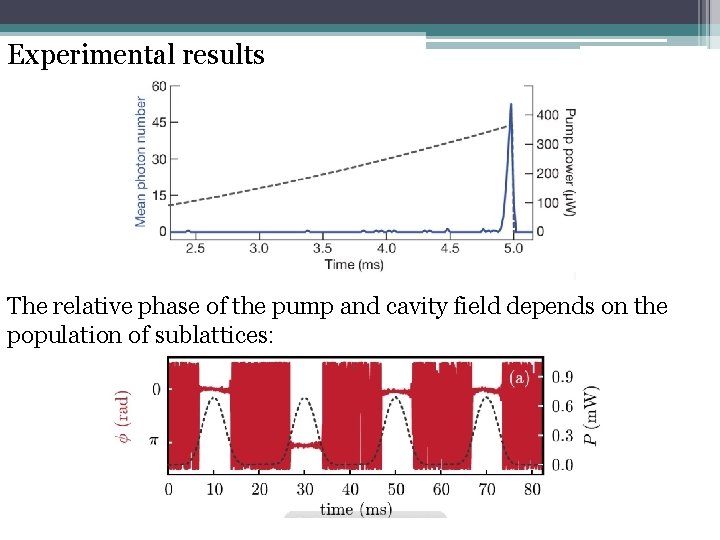
Experimental results The relative phase of the pump and cavity field depends on the population of sublattices:

Statistics of work P(W) Definition: eigenvalue of difference of final and initial ground-state energies probability density function: Fourier-transform characteristic function: appears in fluctuation relations: M. Campisi, et al. Rev. Mod. Phys. 83, 771 (2011) Jarzynski-inequality Tasaki-Crooks relation

Determination of G(u) for the normal phase effective Hamiltonian: diagonalization with Bogoliubov-transformation: eigenfrequencies: protocol: the Hamiltonian contains only the following terms:

Determination of G(u) for the normal phase Heisenberg equation of motion: differential equations for the coefficients with initial conditions where can be expressed in terms of

The characteristic function nth cumulant of the distribution cumulant expansion: expected value: variance: inverse Fourier-transform simple special case: adiabatic process final and initial ground state energies

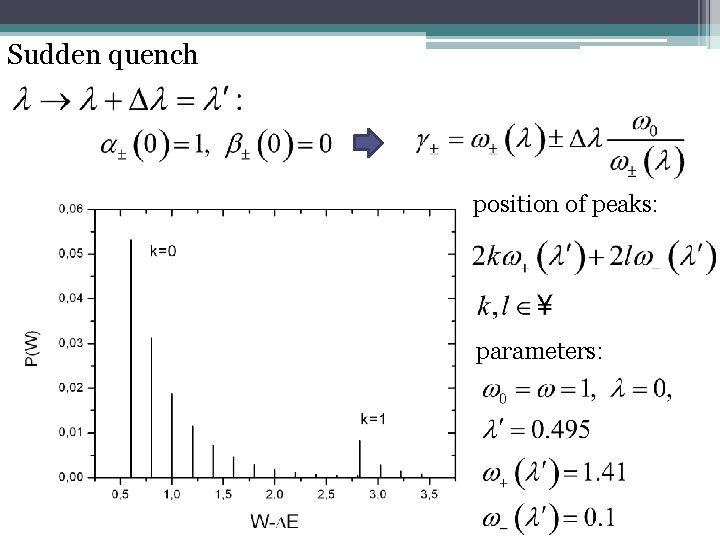
Sudden quench position of peaks: parameters:

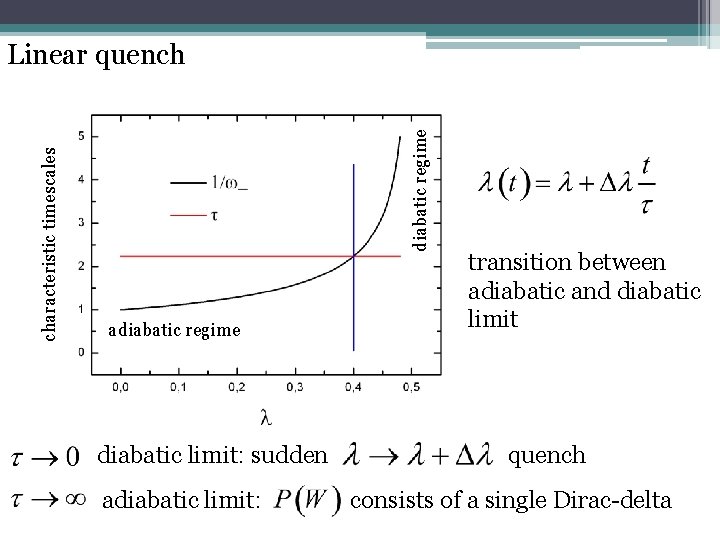
diabatic regime characteristic timescales Linear quench adiabatic regime diabatic limit: sudden adiabatic limit: transition between adiabatic and diabatic limit quench consists of a single Dirac-delta

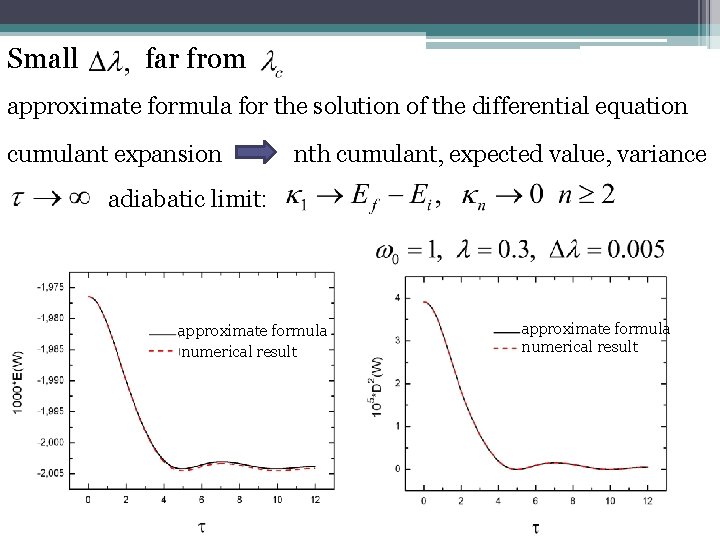
Small far from approximate formula for the solution of the differential equation cumulant expansion nth cumulant, expected value, variance adiabatic limit: approximate formula numerical result

Summary • Quantum-optical models: -Rabi model -Jaynes-Cummings model • Dicke model -Quantum phase transition -Normal and super-radiant phase -Experimental realization • Statistics of work • Characteristic function for the normal phase • Special cases -Sudden quench -Linear quench