Nonequilibrium chiral dynamics and twoparticle correlations in the

Nonequilibrium chiral dynamics and two-particle correlations in the time-dependent variational approach with squeezed states N. Ikezi (Osaka University) M. Asakawa (Osaka University) Y. Tsue (Kochi University)

Contents 1. Introduction Two-particle correlation function in various state Disoriented Chiral Condensate (DCC) 2. Method Time Dependent Variational Approach with squeezed states O(4) linear sigma model Initial condition 3. Numerical Result Domain formation of DCC Spatial correlation Growth of quantum fluctuation Off-diagonal components of Green's function Two particle correlation function 4. Summary

Two particle correlation function Chaotic source for all kinds Hanbury Brown and Twiss effect uses this fact to find source function from a measurement of two particle correlation function.

Two particle correlation function Two particle correlation in various states State Coherent Squeezed Thermal λ 0 -1 < λ< ∞ δkl In the squeezed states, two particle correlation(TPC) varies widely, and its off-diagonal components are finite. → We study TPC in case of DCC formation by using squeezed states.

Formation of Disoriented Chiral Condensate(DCC) Relativistic heavy ion collisions Sigma model Disoriented Chiral Codensate? Chiral restoration Classical approximation Essentially nonequilibrium process ○ Quench × Annealing Amplification of longwalength modes Long range correlation (Formation of DCC domain)

Quantum treatments Homogeneous (Translationally invariant) × Long range correlation Inhomogeneous mean fields ? Thermalization →Green’s function is diagonal in momentum space ! (homogeneous) The DCC domain formation is not yet observed We study the dynamics of chiral phase transition in spatially inhomogeneous systems with mode-mode correlation in the framework of Time Dependent Variational Approach (TDVA) with squeezed states. What will be happen to two particle correlation function?

Time-dependent variational approach with Y. Tsue, Y. Fujiwara Prog. Theor. Phys. 86 (1991) 469 squeezed states R. Jackiw, A. K. Kerman Phys. Lett. 71 A (1979) 158 Squeezed State has large & closed functional space Mode-mode coupling Mean Field C(x, t) : Mean field (condensate) D(x, t) : Conjugate variable for C(x, t) Fluctuation and correlation G(x, x’, t) : Quantum fluctuation and correlation Π(x, x’, t) : Conjugate variable for G(x, x’, t) Time-dependent Variational　Principle

O(4) linear sigma model Hamiltonian Variables Mean fields(chiral order parameter) Quantum fluctuations and correlations Parameters

Quench initial condition ◇ Mean fields(chiral order parameters) Randomly distributed according to the Gaussian form with the following parameters …. . Ci Ci+1 ◇ Quantum fluctuation and correlation We assume that the sigma and pion fields are in a coherent state with the degenerate mass m 0. (Diagonal in momentum space)

Numerical results To understand the role of the mode-mode correlations, we performed numerical calculations for the following two cases: Mode-mode correlation Case A ○ Case B × Setup Dimension 3+1 → 1+1

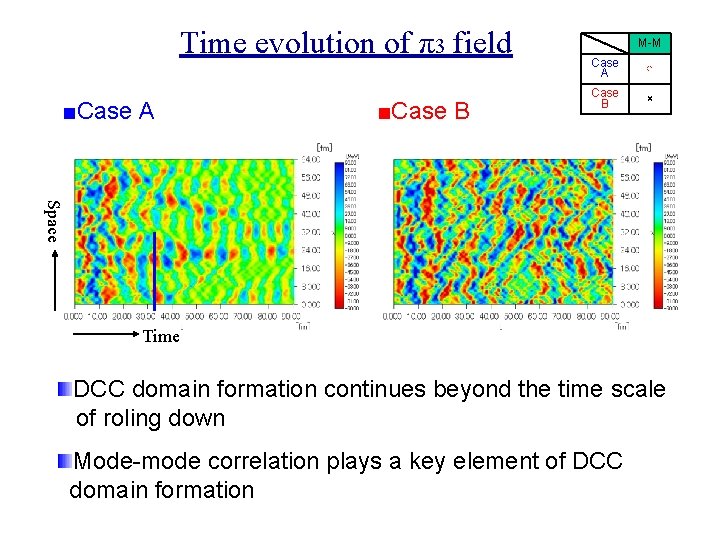
Time evolution of π3 field ■Case A ■Case B M-M Case A ○ Case B × Space Time DCC domain formation continues beyond the time scale of roling down Mode-mode correlation plays a key element of DCC domain formation

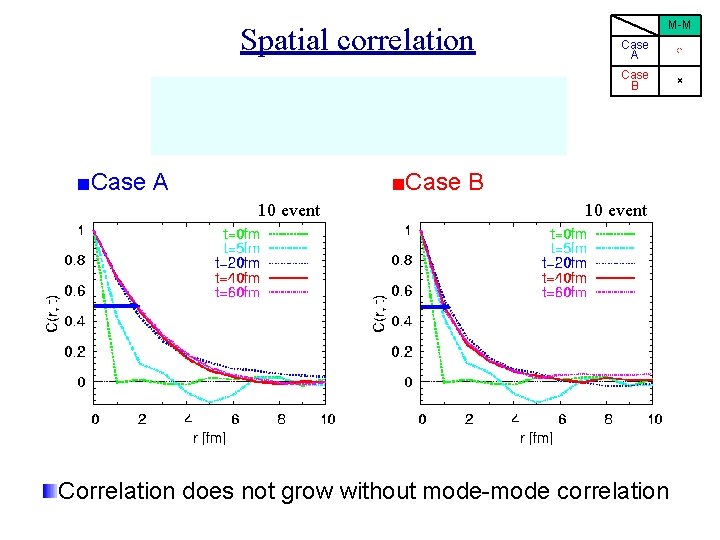
Spatial correlation ■Case A M-M Case A ○ Case B × ■Case B 10 event Correlation does not grow without mode-mode correlation

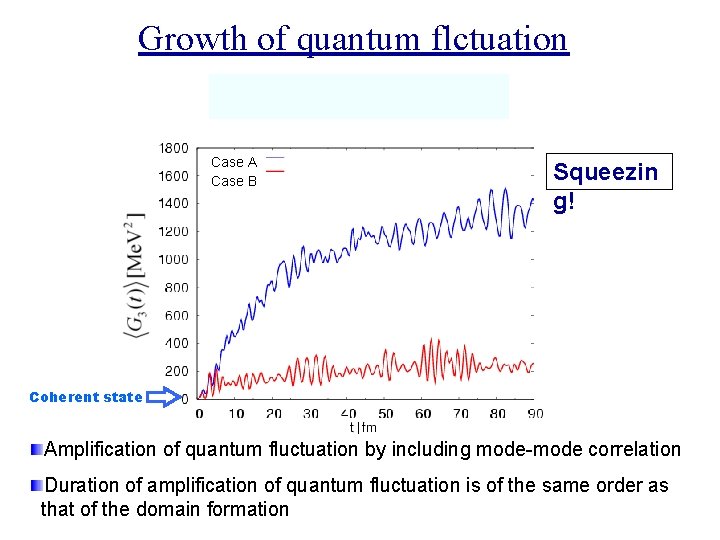
Growth of quantum flctuation Case A Case B Squeezin g! Coherent state Amplification of quantum fluctuation by including mode-mode correlation Duration of amplification of quantum fluctuation is of the same order as that of the domain formation

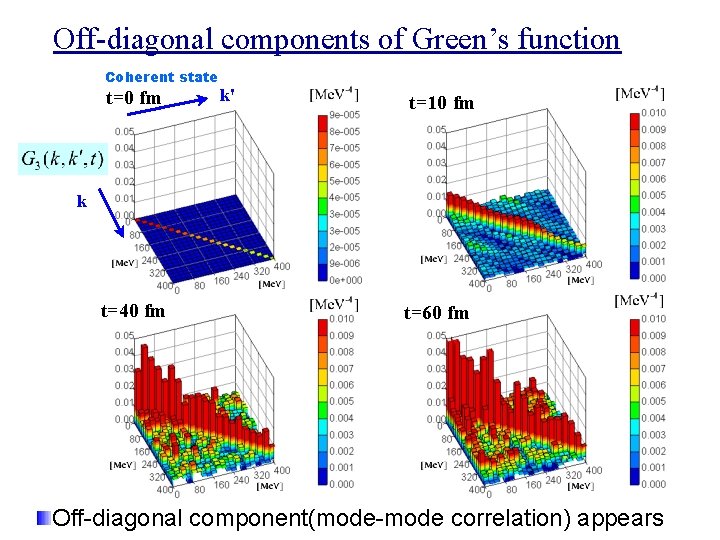
Off-diagonal components of Green’s function Coherent state t=0 fm k' t=10 fm k t=40 fm t=60 fm Off-diagonal component(mode-mode correlation) appears

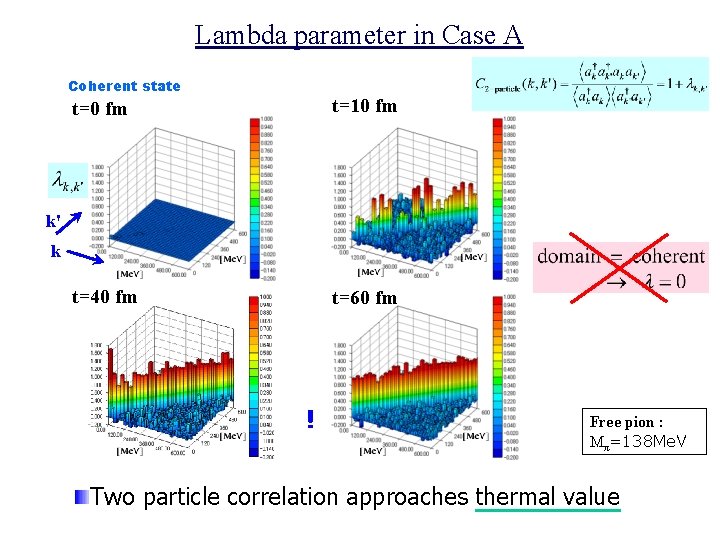
Lambda parameter in Case A Coherent state t=0 fm t=10 fm t=40 fm t=60 fm k' k ! Free pion : Mπ=138 Me. V Two particle correlation approaches thermal value

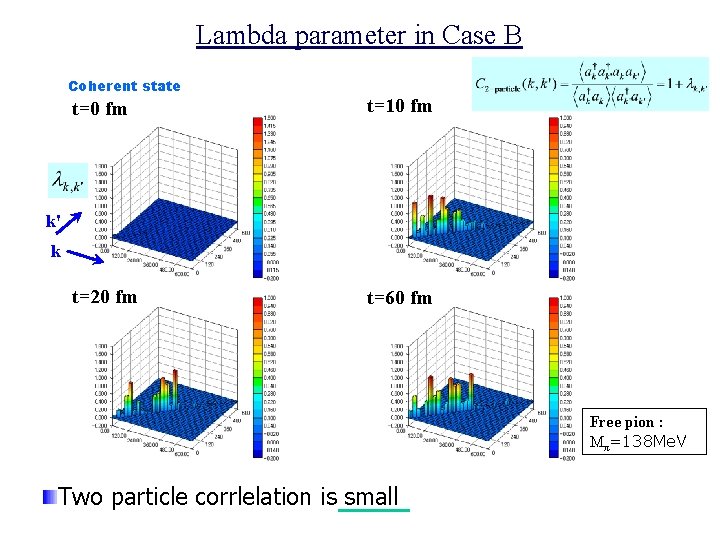
Lambda parameter in Case B Coherent state t=0 fm t=10 fm t=20 fm t=60 fm k' k Free pion : Mπ=138 Me. V Two particle corrlelation is small

Summary Dynamics of chiral phase transition in spatially inhomogeneous systems with mode-mode correlation was studied in the framework of TDVA with squeezed states. In quantum treatment, the mode-mode correlation plays an important role in the formation of DCC. Time evolutions of two particle correlation (TPC) were studied. In the case with mode-mode correlation, TPC approaches thermal value in spite of the existence of DCC domain and non-zero mode correlation. Future works: ▪ Realistic geometry in relativistic heavy ion collisions ▪ Extension to higher spatial dimensions 1+1 → 1+2, 1+3 ▪ Including finite size effect into the analysis of TPC

Energy conservation

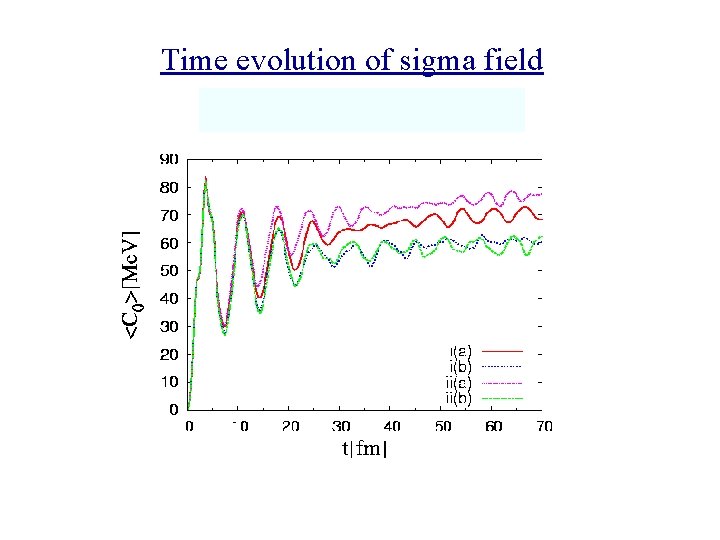
Time evolution of sigma field

Two particle correlation function in squeezed state Quantum mechanics (single mode)

Time-dependent Variational　Principle Equations of motion