NonDeterministic Finite Automata 1 Nondeterministic Finite Automaton NFA





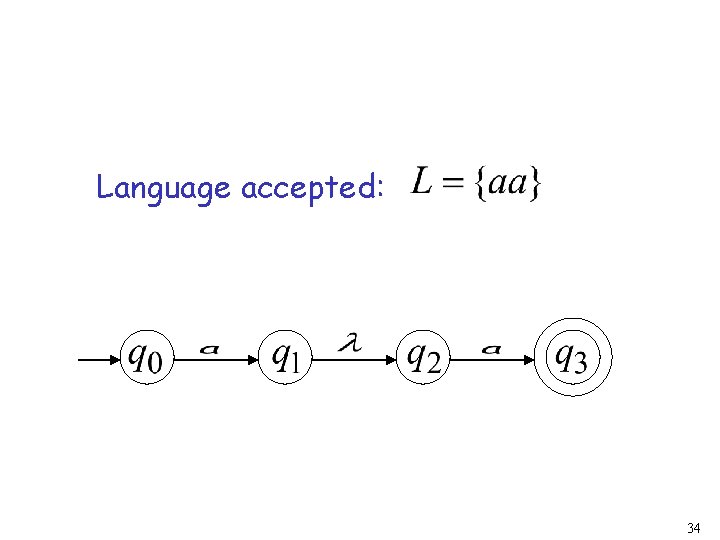














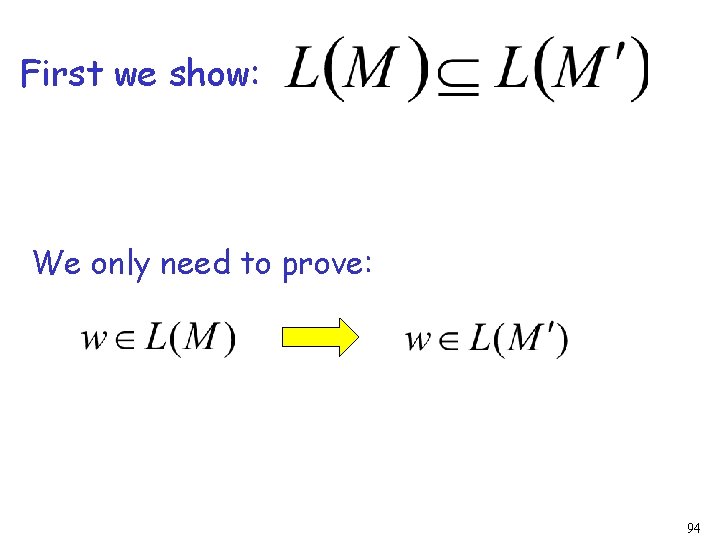


- Slides: 104

Non-Deterministic Finite Automata 1

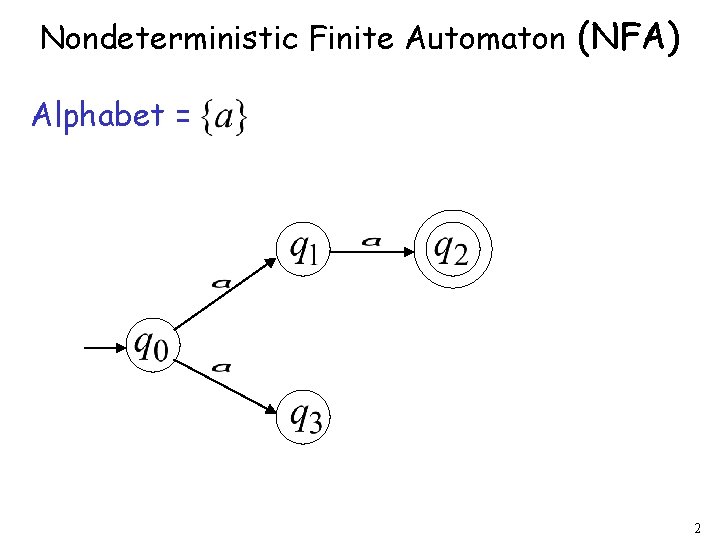
Nondeterministic Finite Automaton (NFA) Alphabet = 2

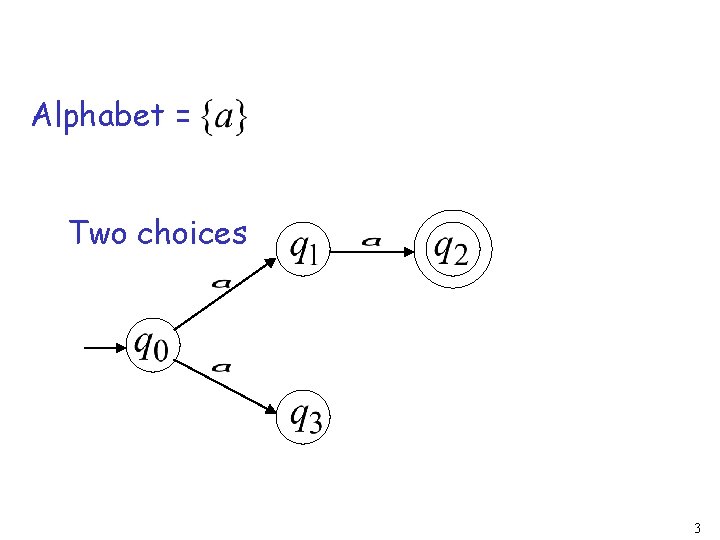
Alphabet = Two choices 3

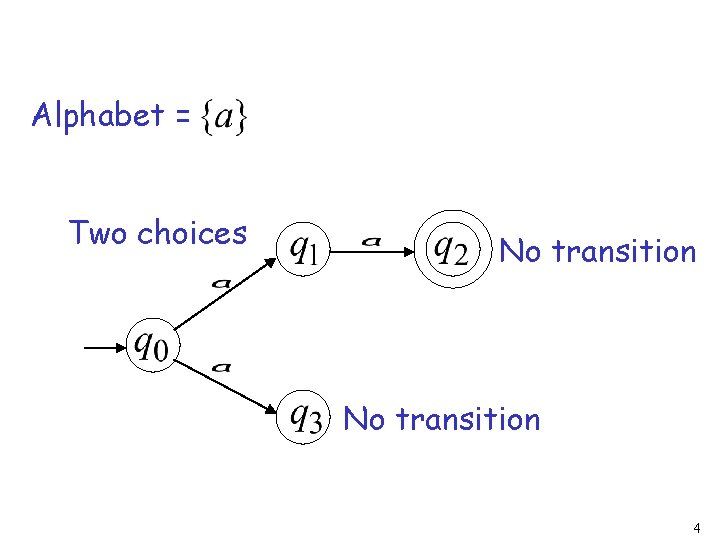
Alphabet = Two choices No transition 4

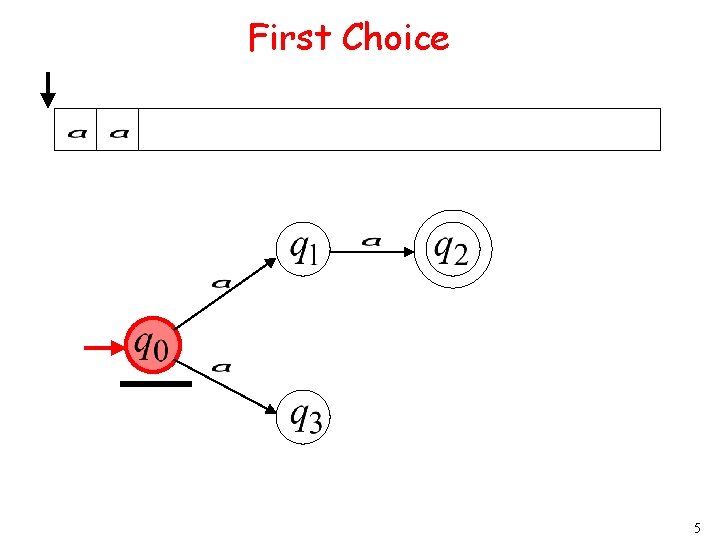
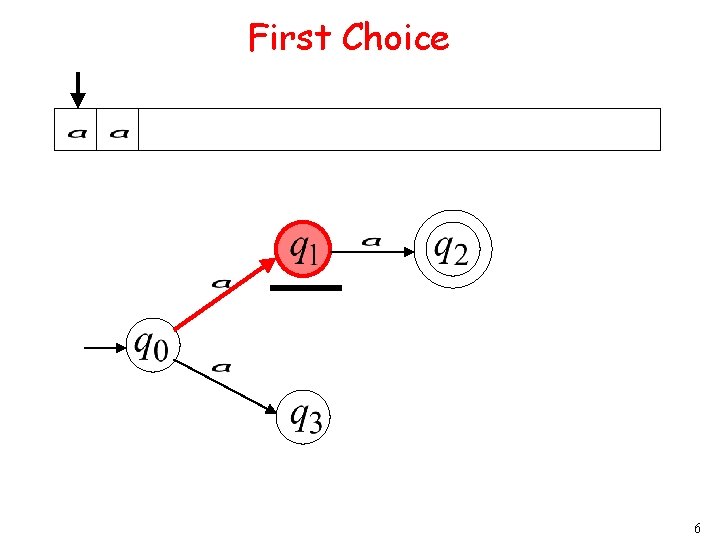
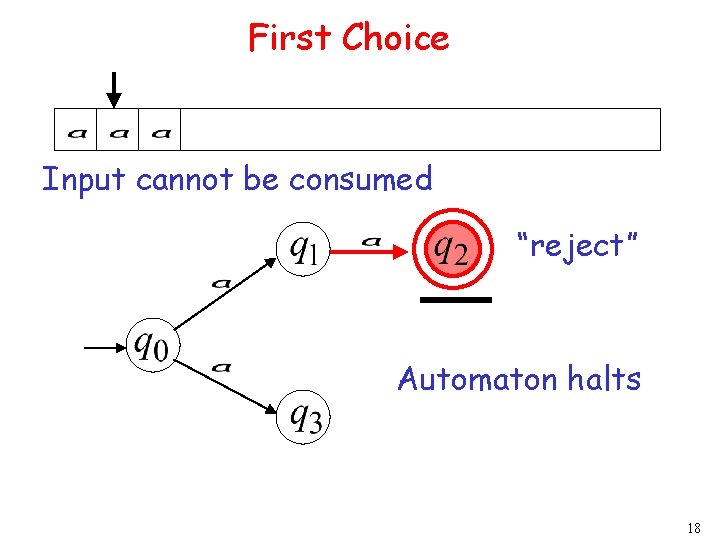
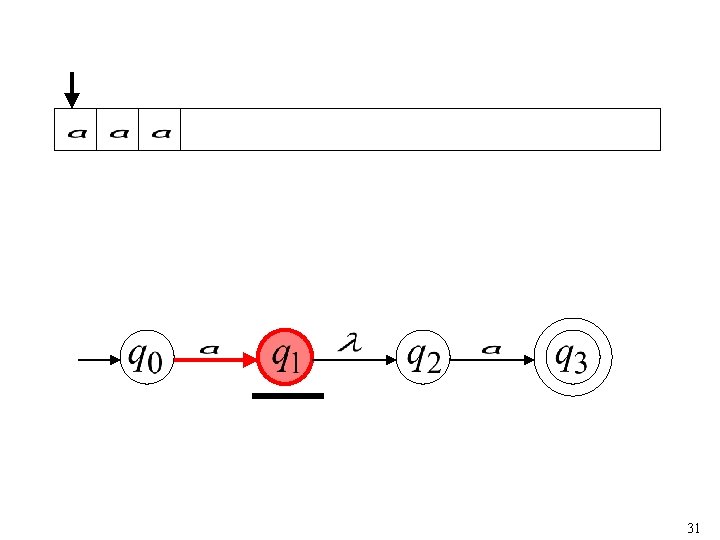
First Choice 5

First Choice 6

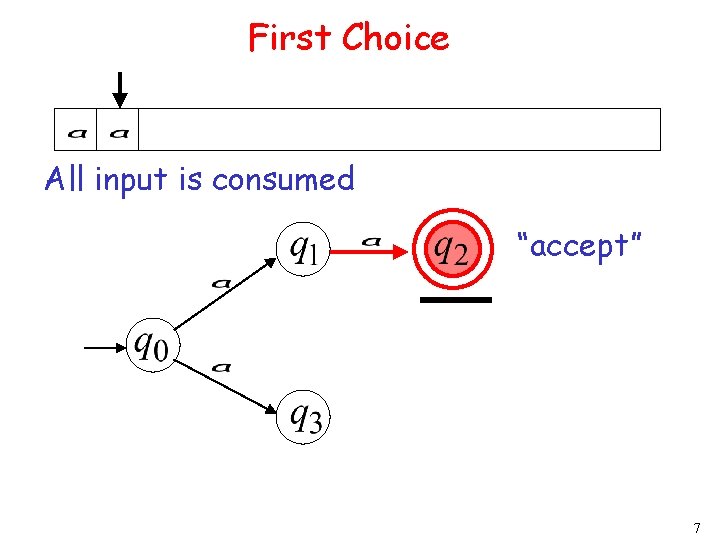
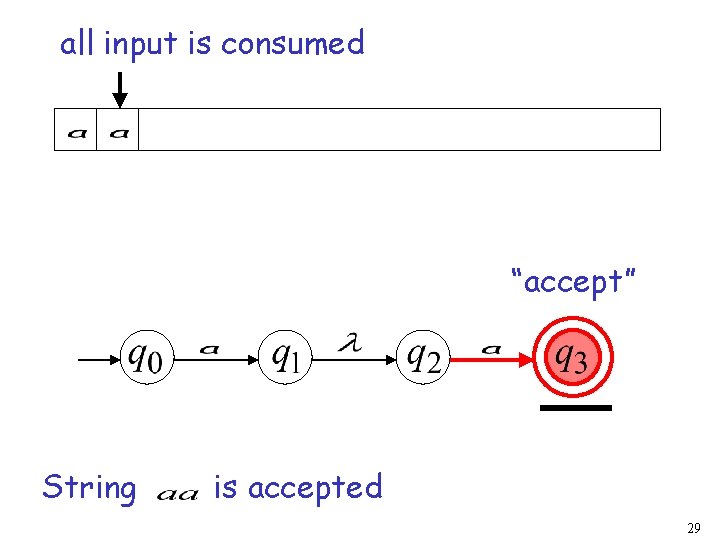
First Choice All input is consumed “accept” 7

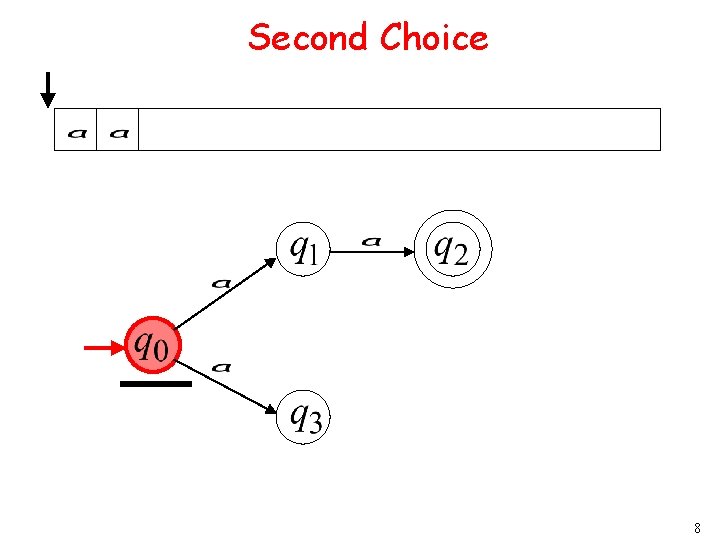
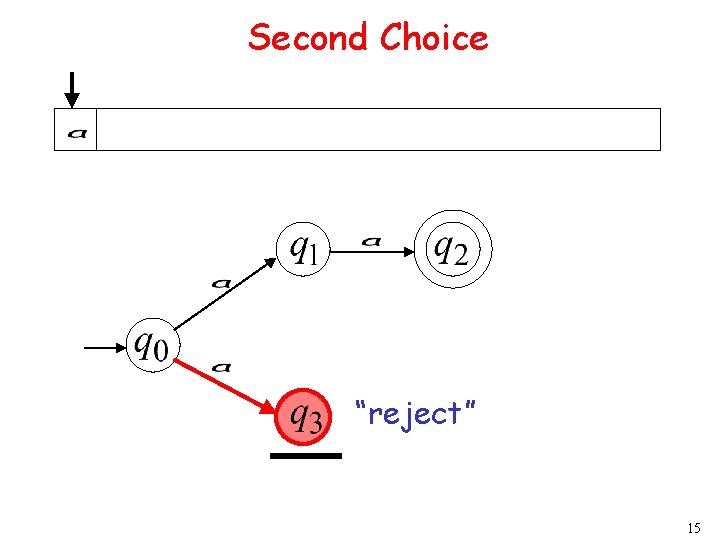
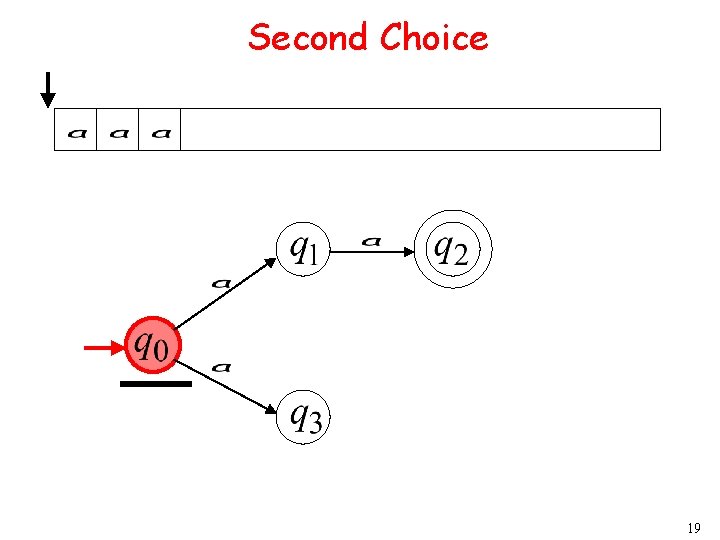
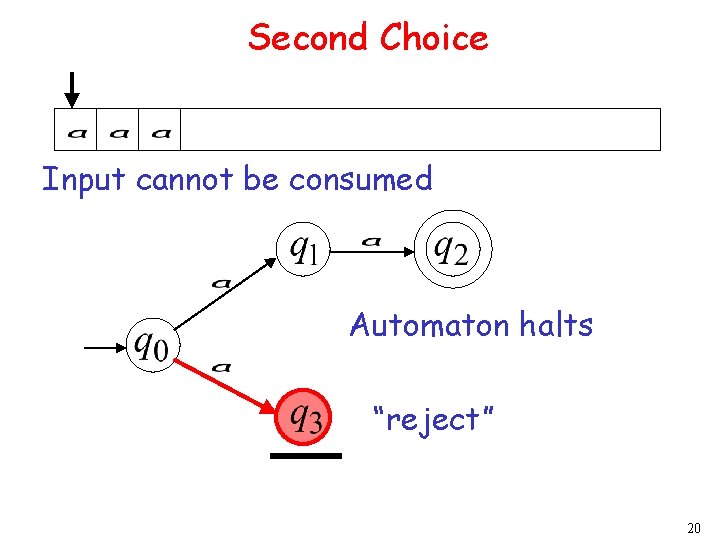
Second Choice 8

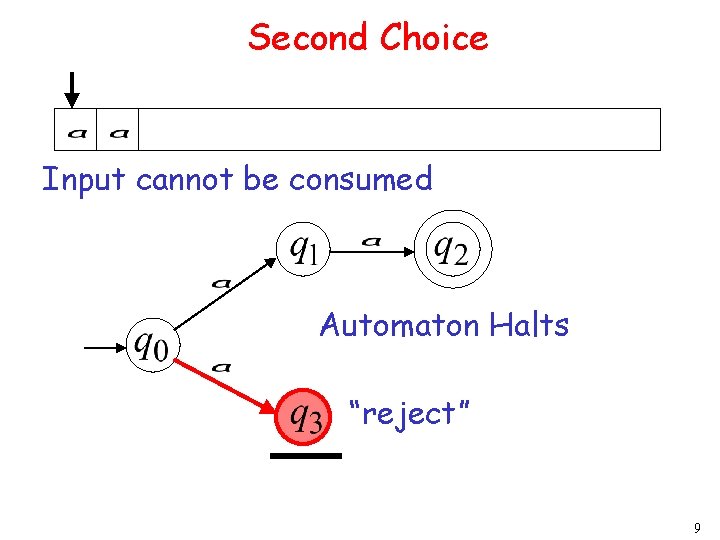
Second Choice Input cannot be consumed Automaton Halts “reject” 9

An NFA accepts a string: if there is a computation of the NFA that accepts the string i. e. , all the input string is processed and the automaton is in an accepting state 10

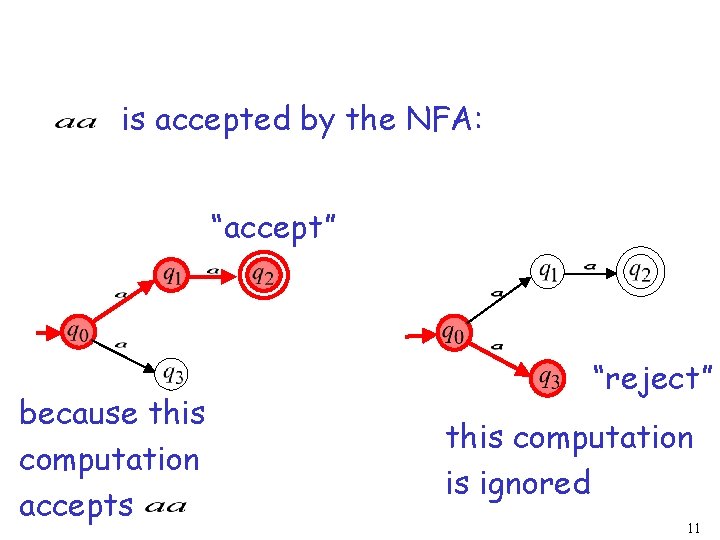
is accepted by the NFA: “accept” because this computation accepts “reject” this computation is ignored 11

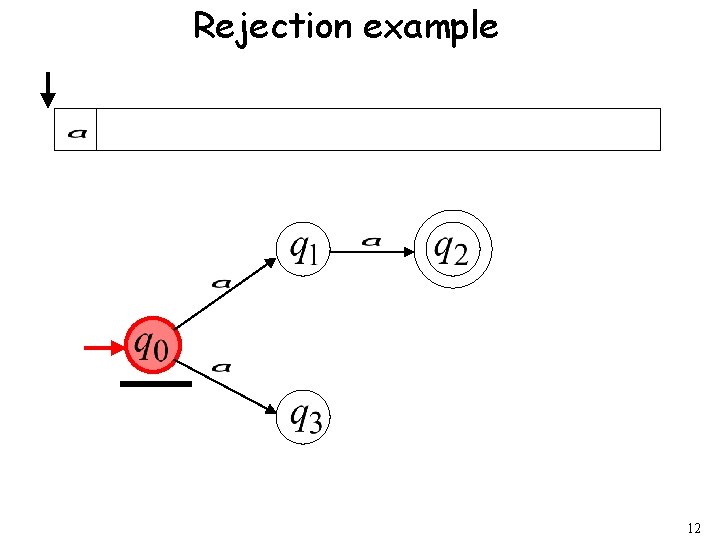
Rejection example 12

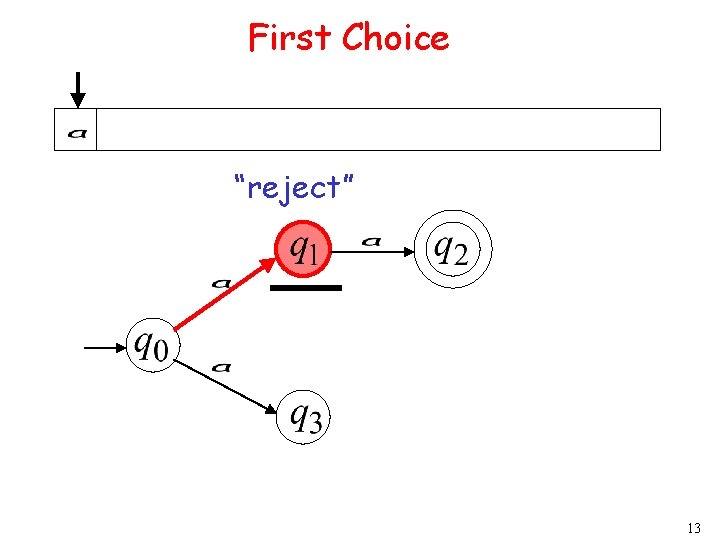
First Choice “reject” 13

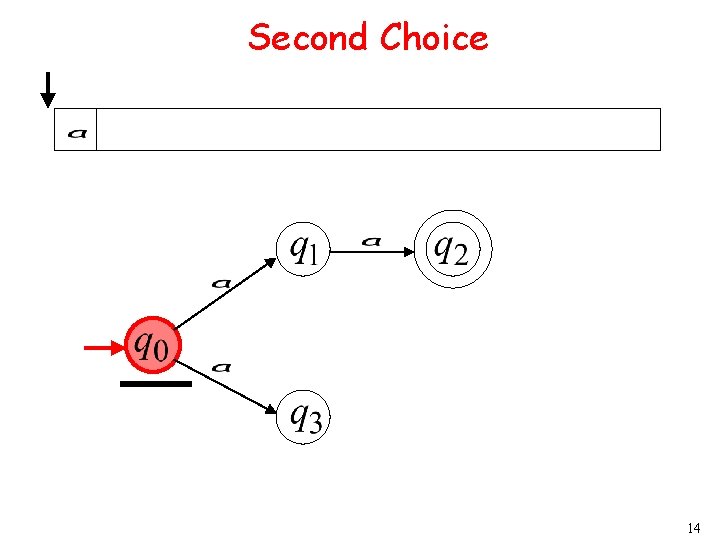
Second Choice 14

Second Choice “reject” 15

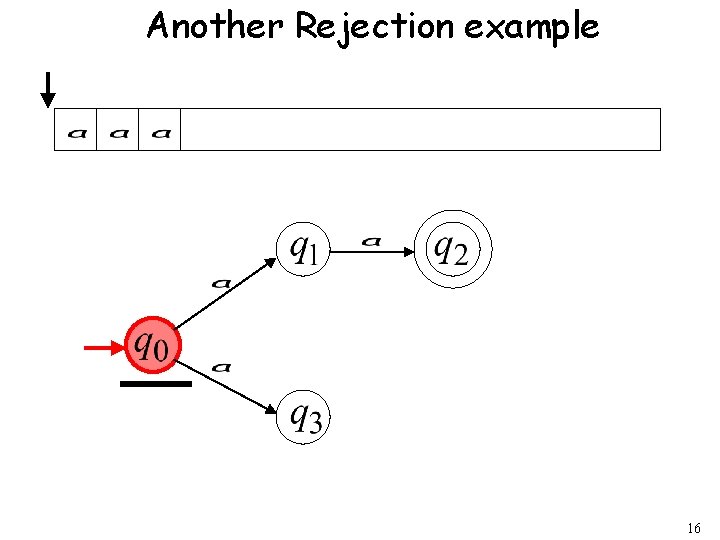
Another Rejection example 16

First Choice 17

First Choice Input cannot be consumed “reject” Automaton halts 18

Second Choice 19

Second Choice Input cannot be consumed Automaton halts “reject” 20

An NFA rejects a string: if there is no computation of the NFA that accepts the string. For each computation: • All the input is consumed and the automaton is in a non final state OR • The input cannot be consumed 21

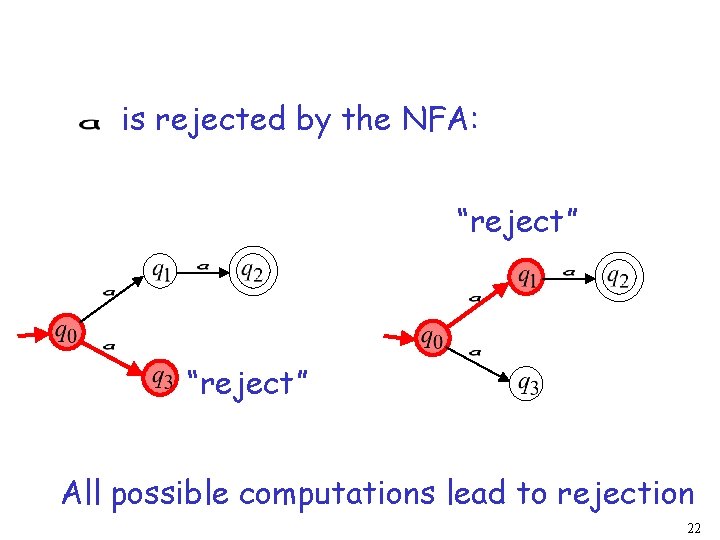
is rejected by the NFA: “reject” All possible computations lead to rejection 22

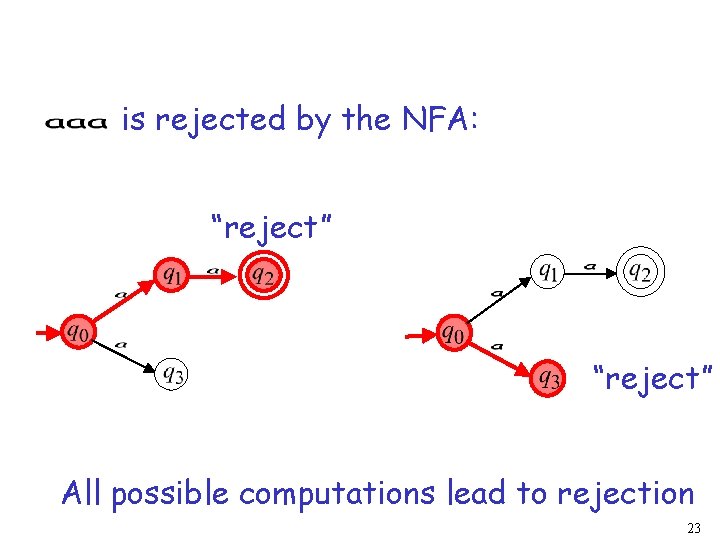
is rejected by the NFA: “reject” All possible computations lead to rejection 23

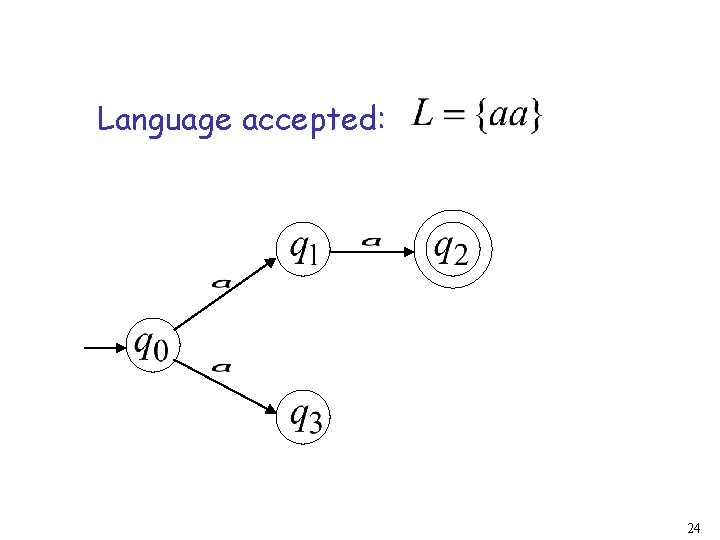
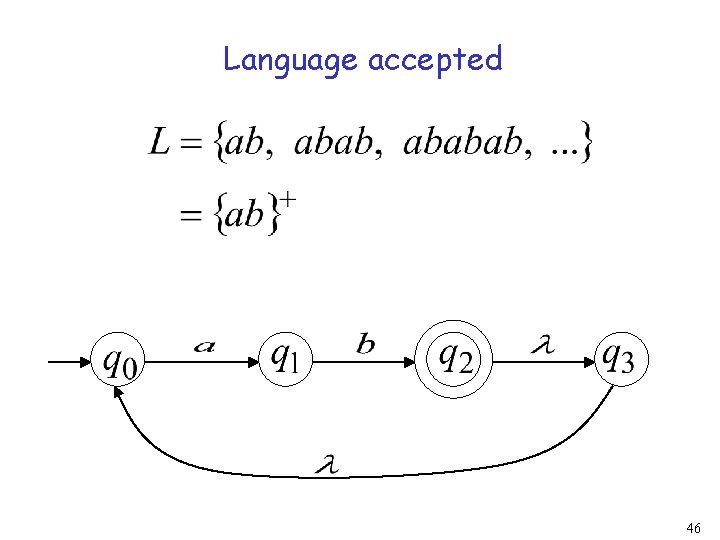
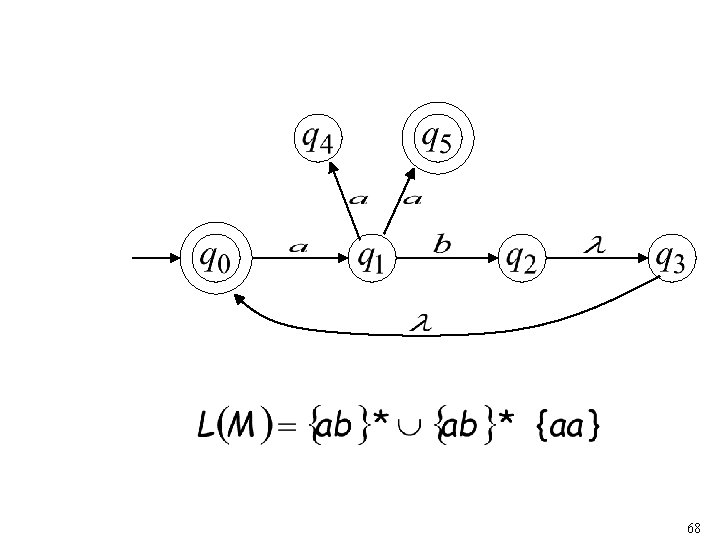
Language accepted: 24

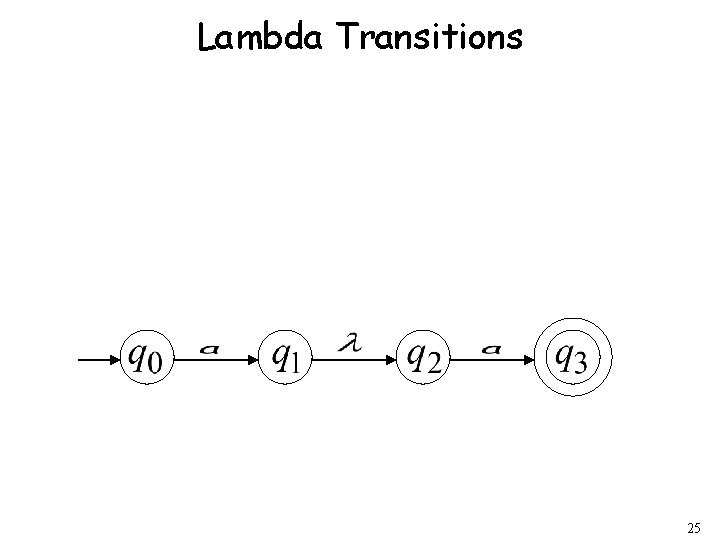
Lambda Transitions 25

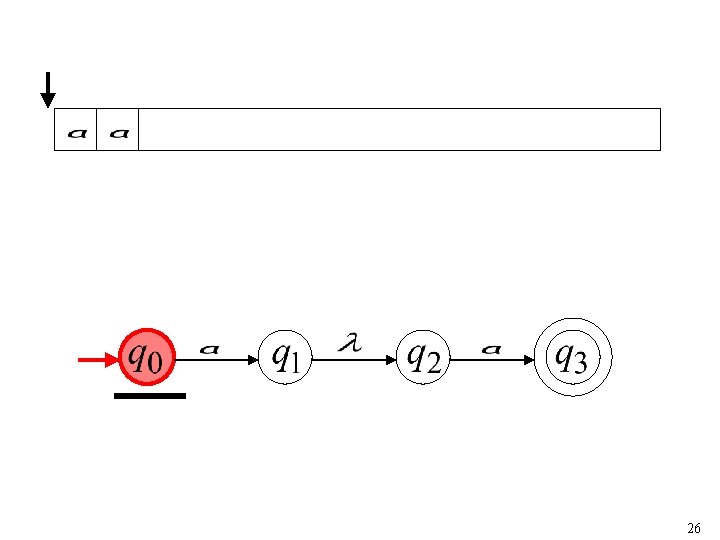
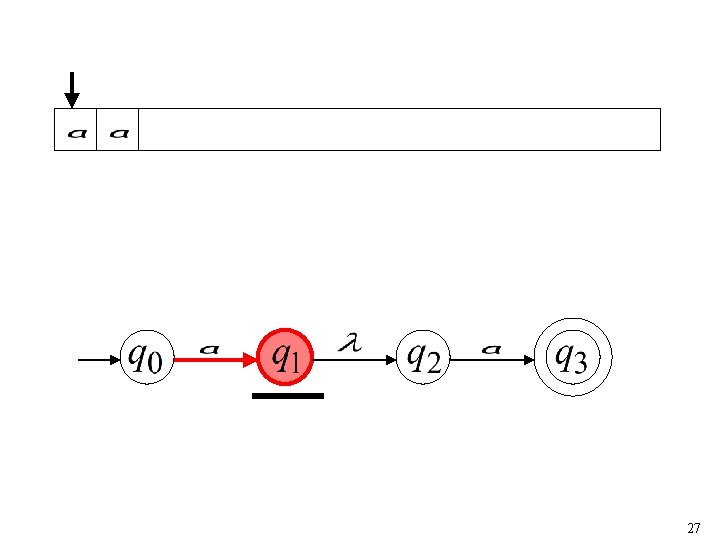
26

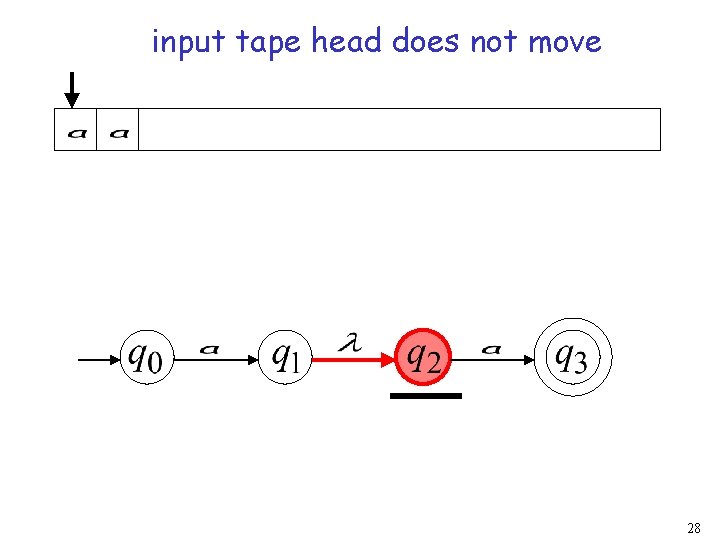
27

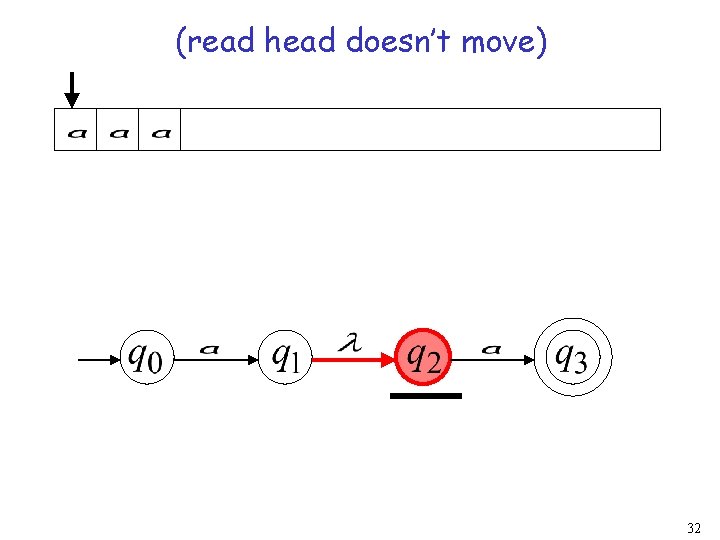
input tape head does not move 28

all input is consumed “accept” String is accepted 29

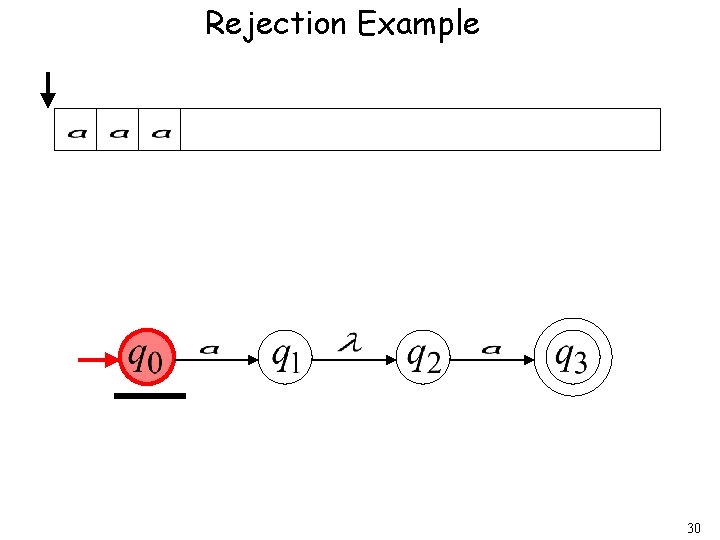
Rejection Example 30

31

(read head doesn’t move) 32

Input cannot be consumed Automaton halts “reject” String is rejected 33
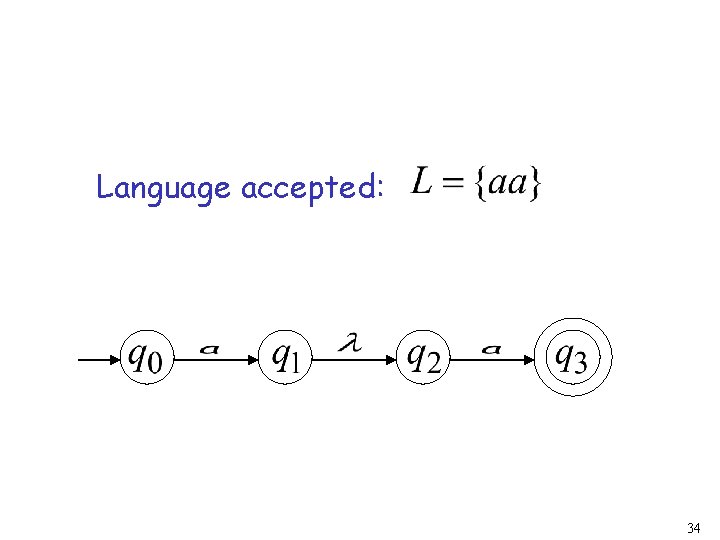
Language accepted: 34

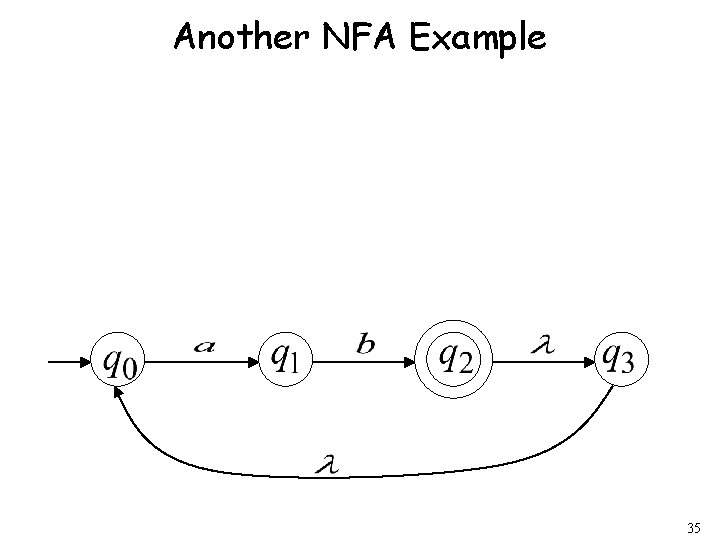
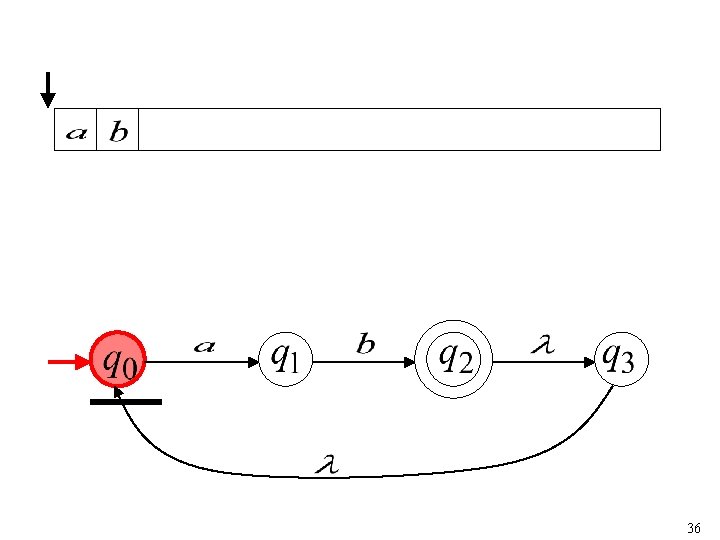
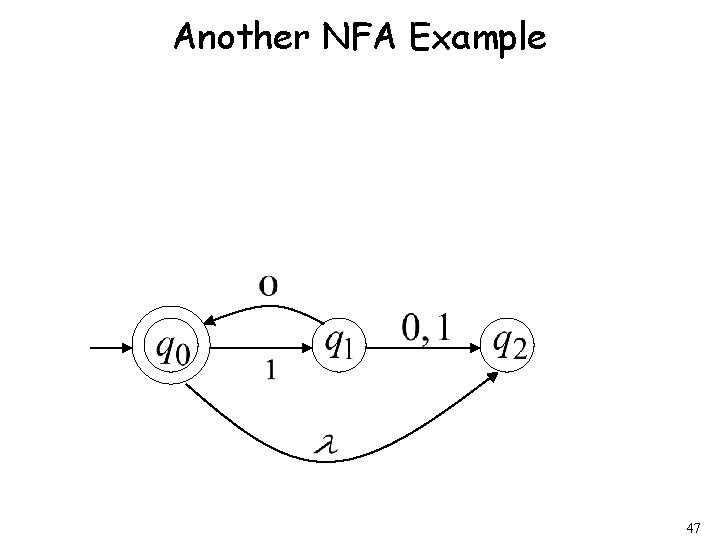
Another NFA Example 35

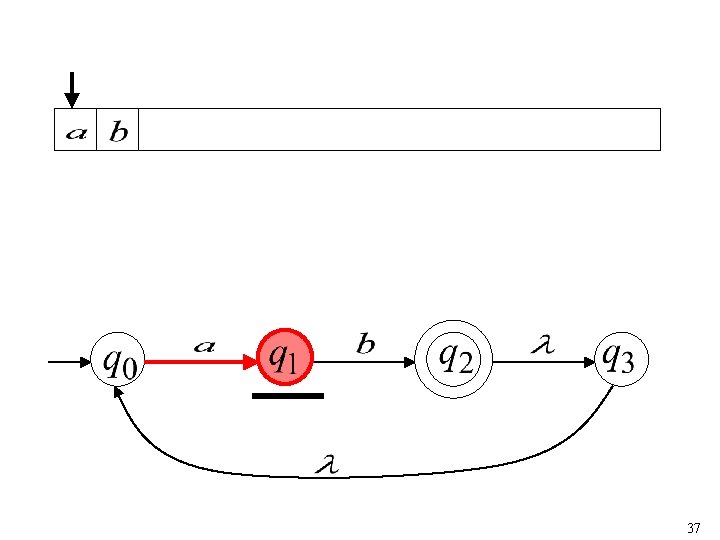
36

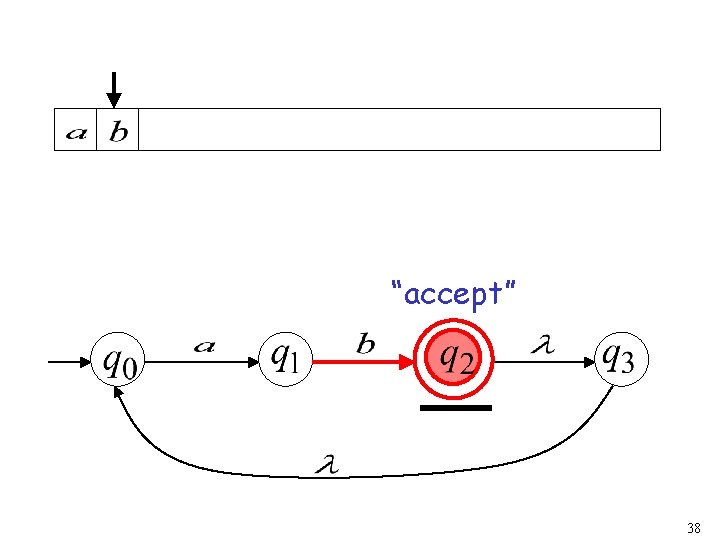
37

“accept” 38

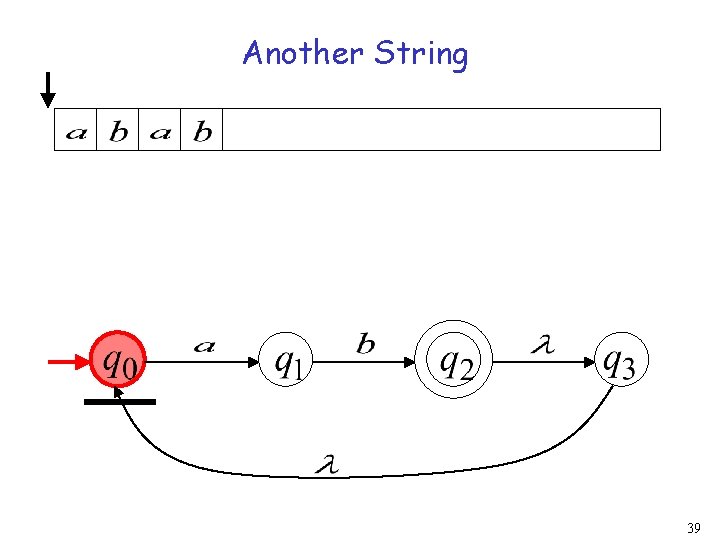
Another String 39

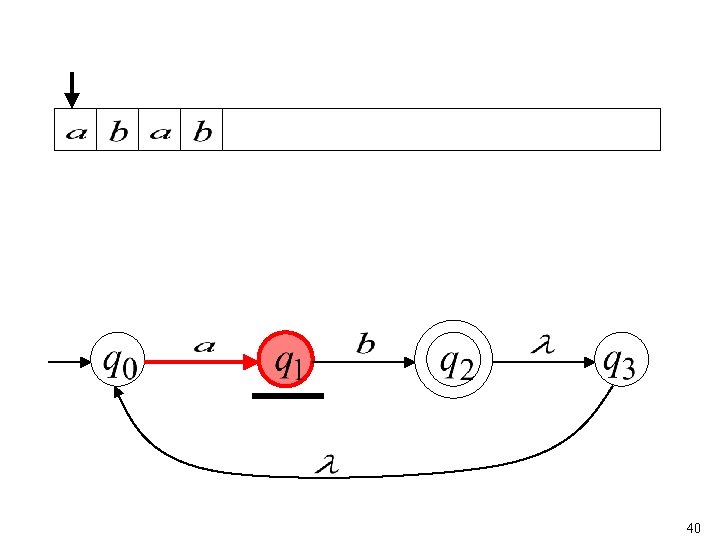
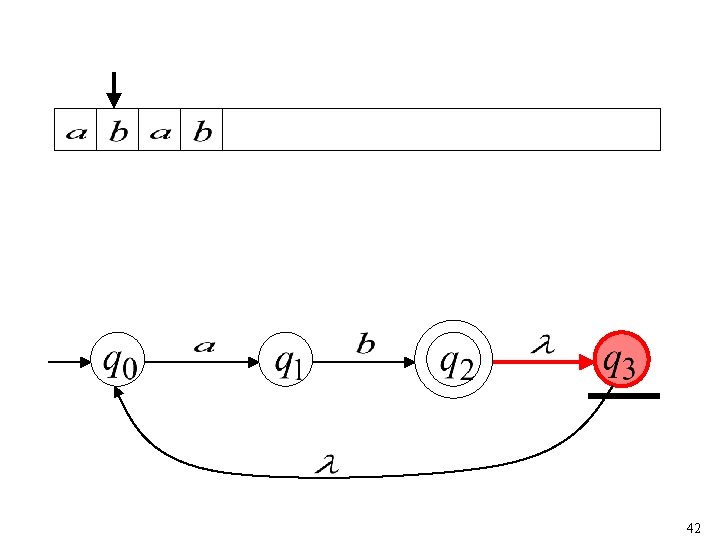
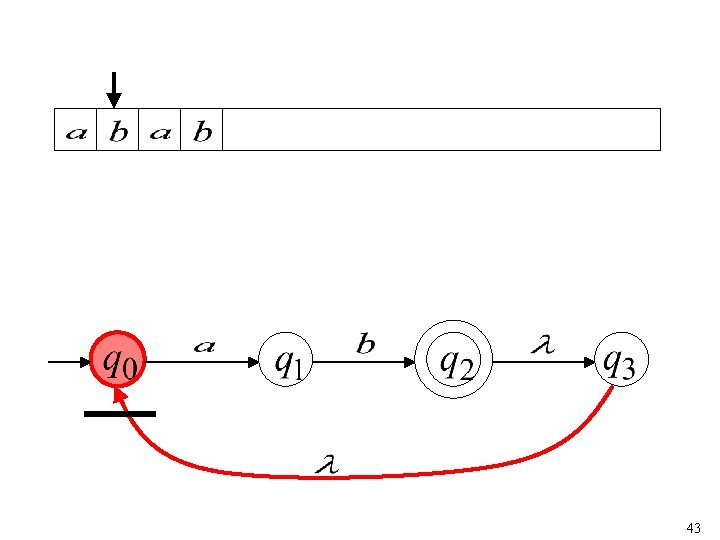
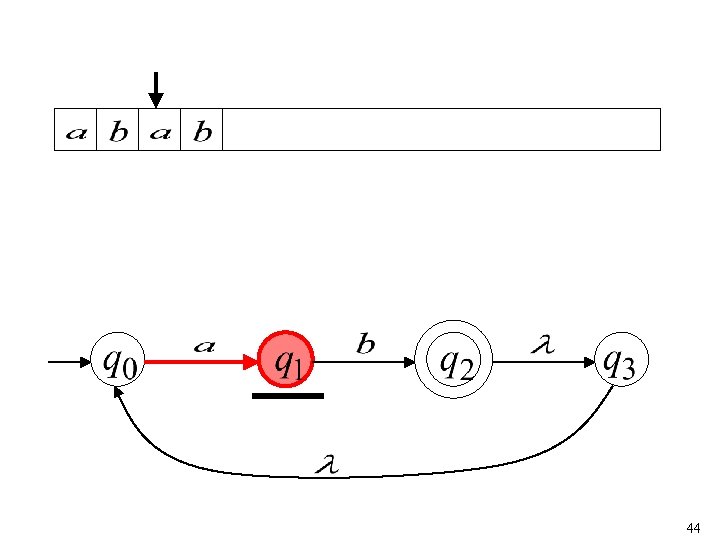
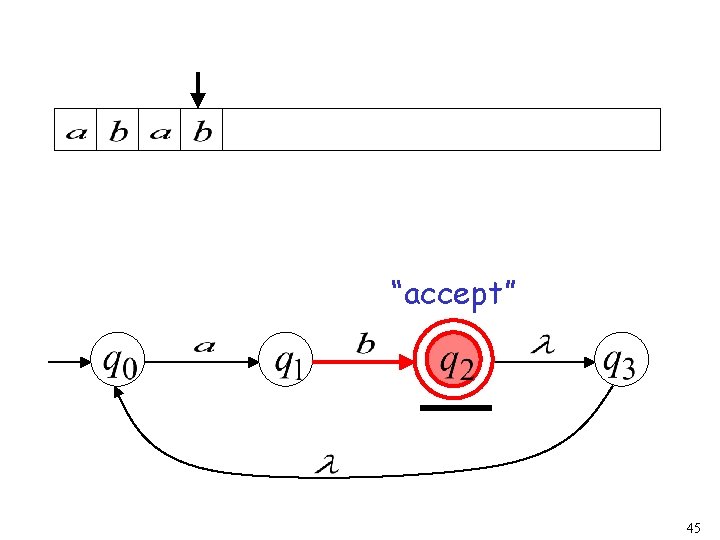
40

41

42

43

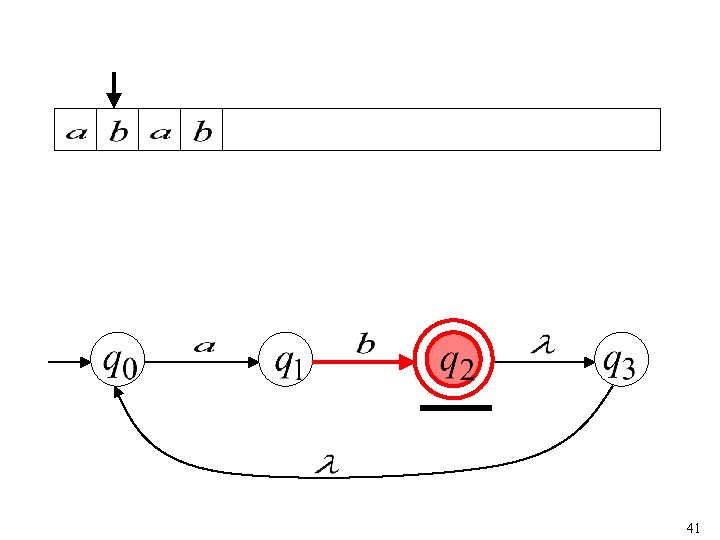
44

“accept” 45

Language accepted 46

Another NFA Example 47

Language accepted (redundant state) 48

Remarks: • The symbol never appears on the input tape • Simple automata: 49

• NFAs are interesting because we can express languages easier than DFAs NFA DFA 50

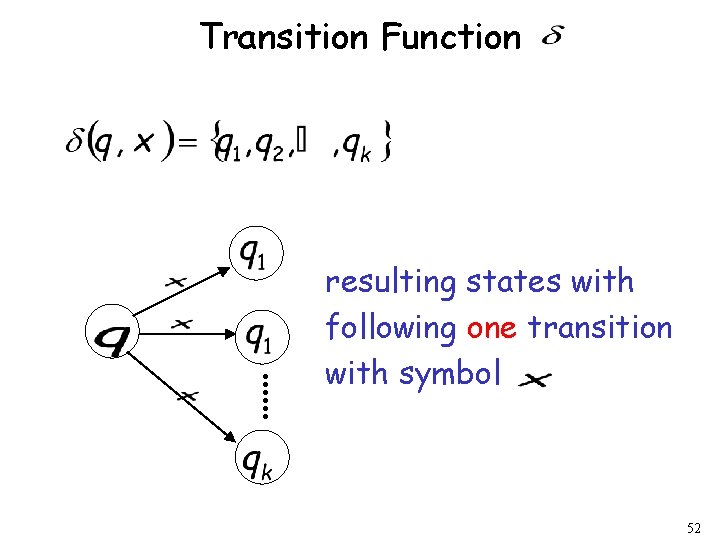
Formal Definition of NFAs Set of states, i. e. Input aplhabet, i. e. Transition function Initial state Accepting states 51

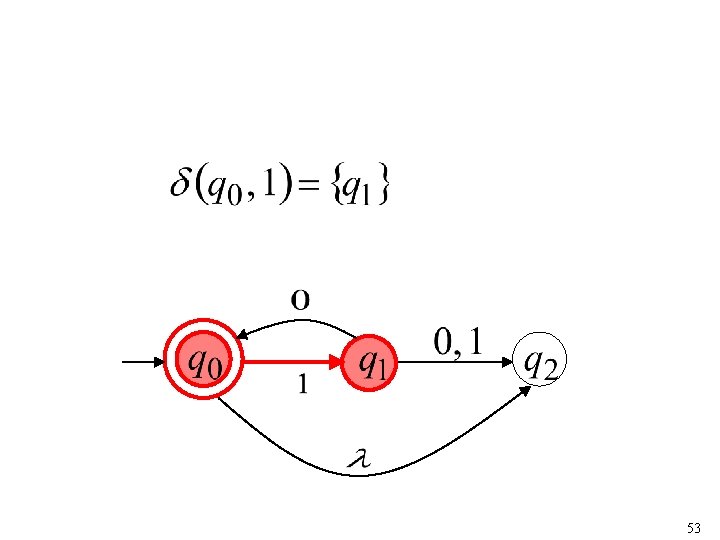
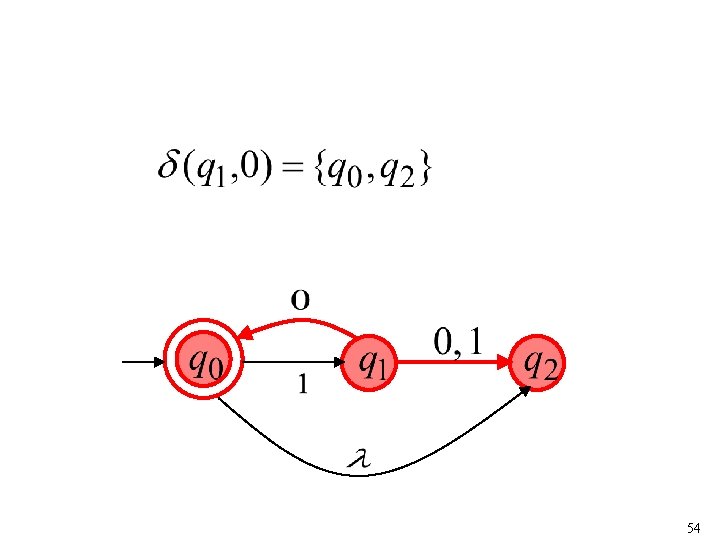
Transition Function resulting states with following one transition with symbol 52

53

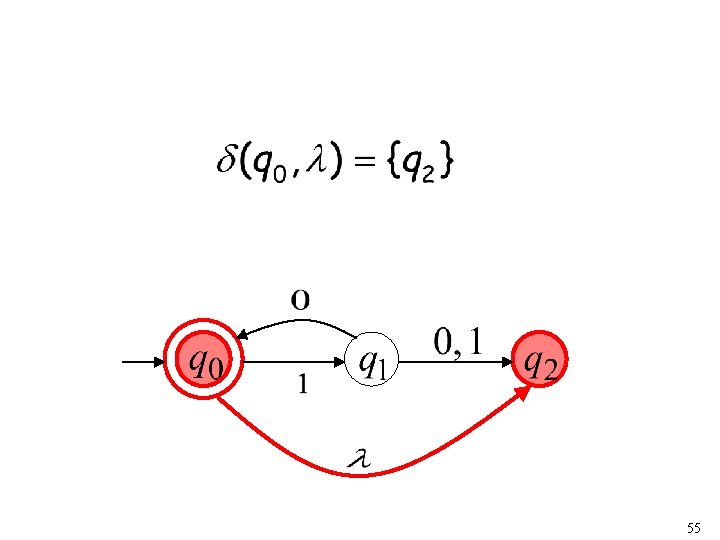
54

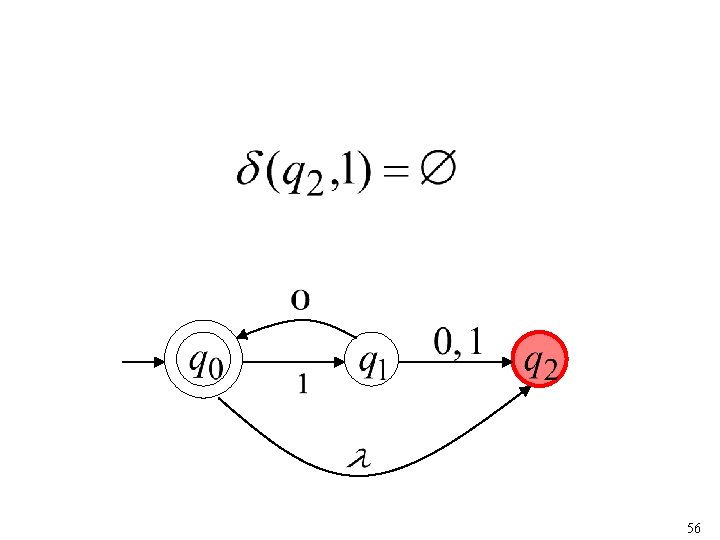
55

56

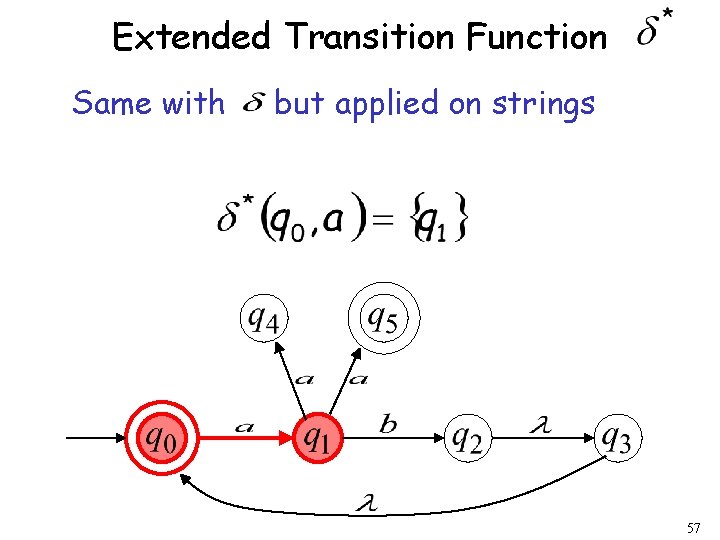
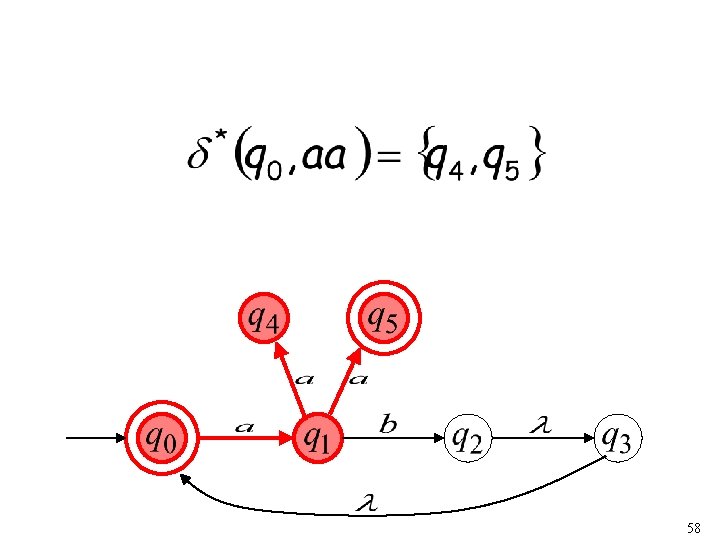
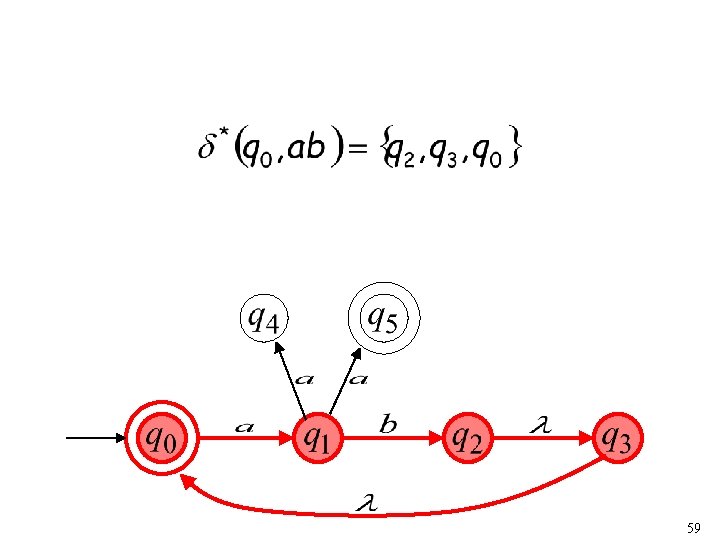
Extended Transition Function Same with but applied on strings 57

58

59

Special case: for any state 60

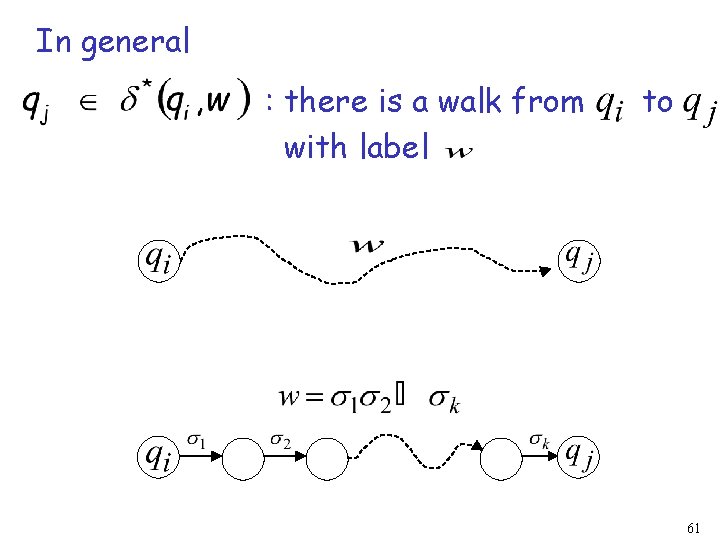
In general : there is a walk from with label to 61

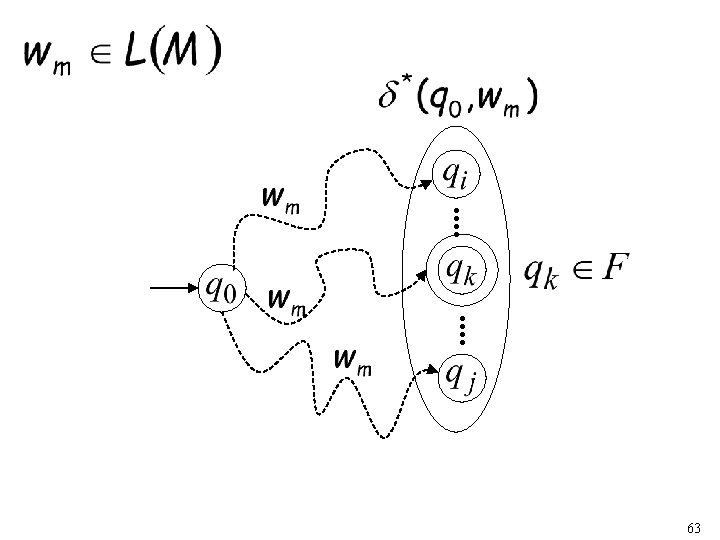
The Language of an NFA The language accepted by is: where and there is some (accepting state) 62

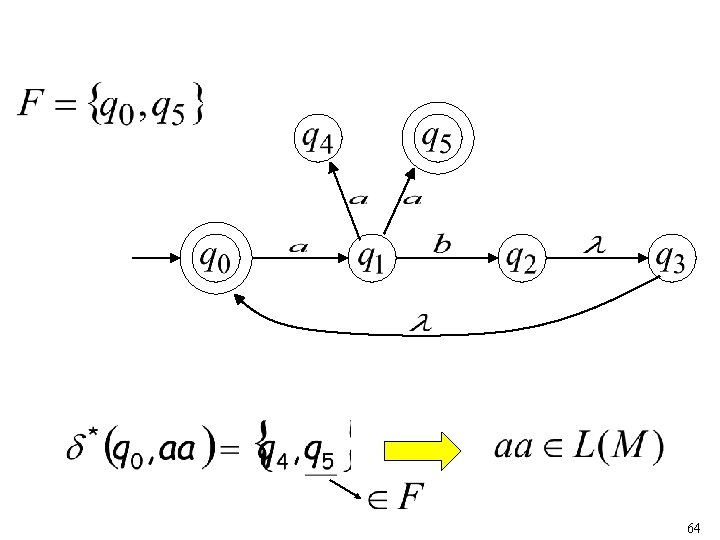
63

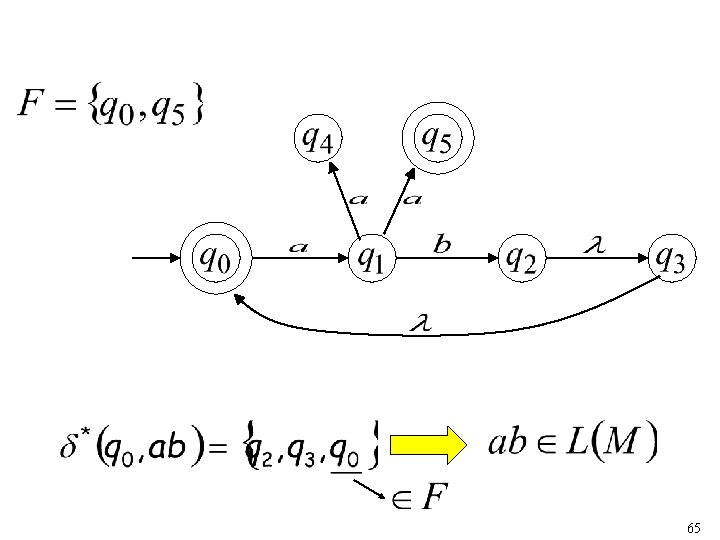
64

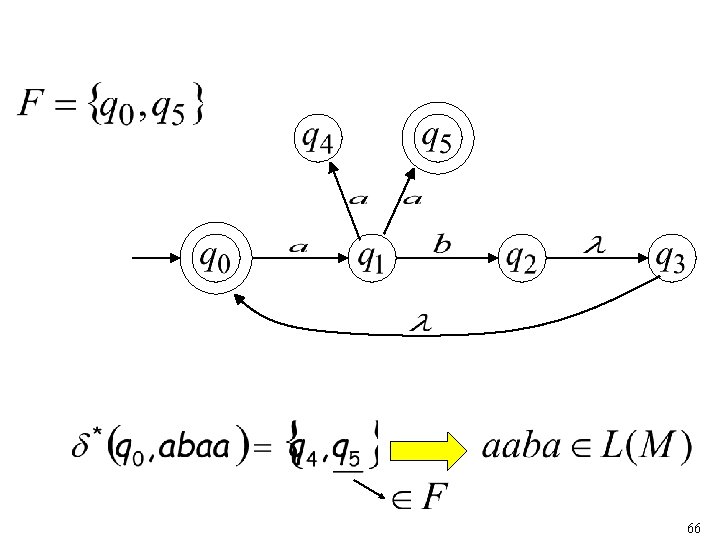
65

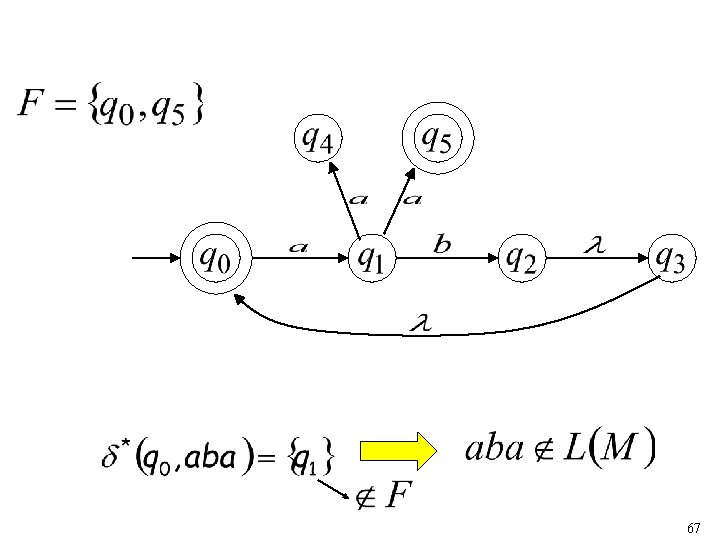
66

67

68

NFAs accept the Regular Languages 69

Equivalence of Machines Definition: Machine is equivalent to machine if 70

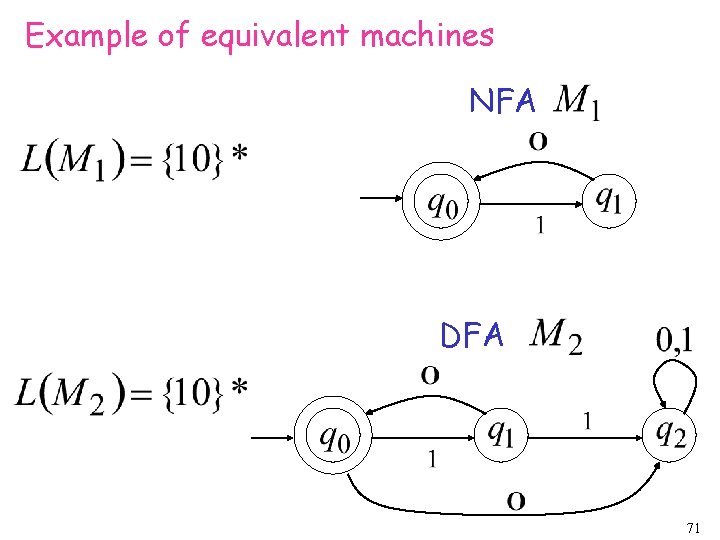
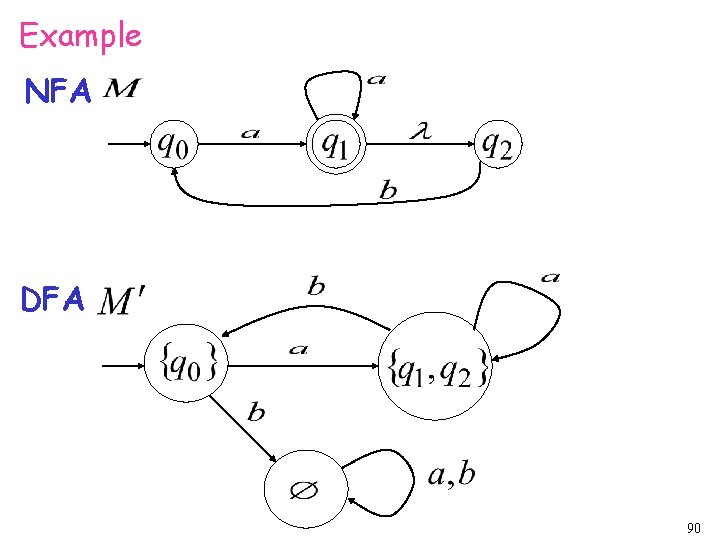
Example of equivalent machines NFA DFA 71

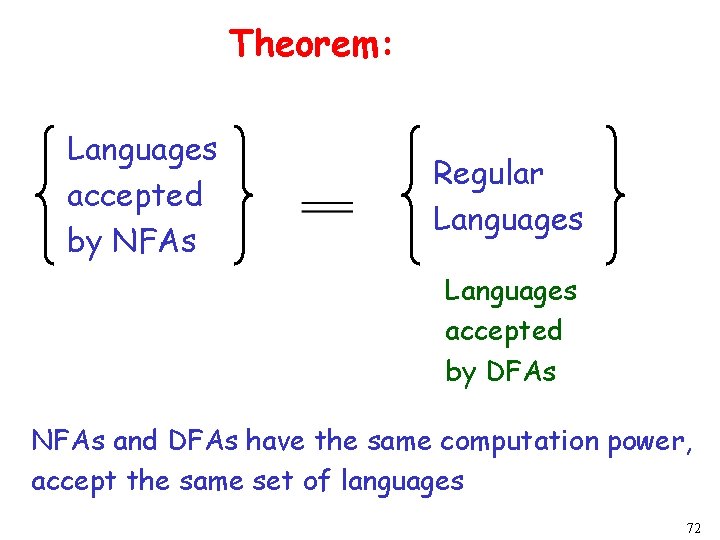
Theorem: Languages accepted by NFAs Regular Languages accepted by DFAs NFAs and DFAs have the same computation power, accept the same set of languages 72

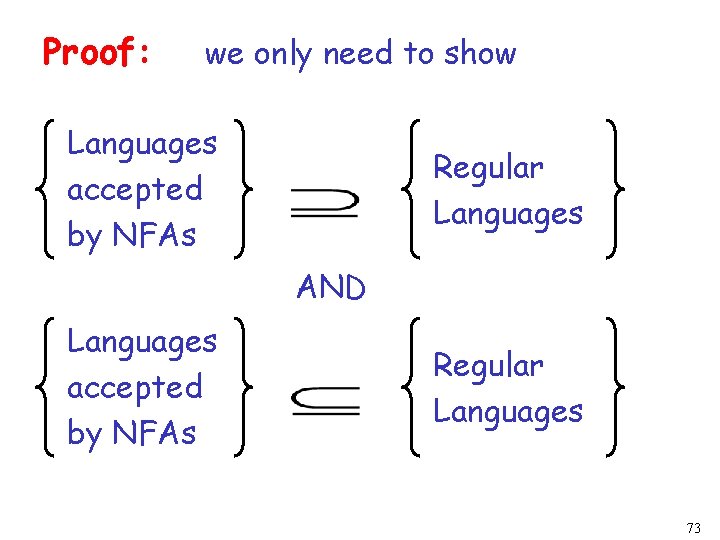
Proof: we only need to show Languages accepted by NFAs Regular Languages AND Languages accepted by NFAs Regular Languages 73

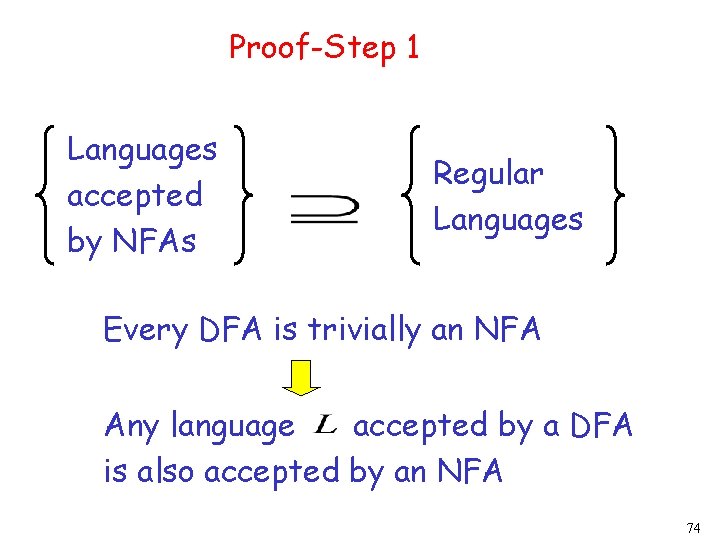
Proof-Step 1 Languages accepted by NFAs Regular Languages Every DFA is trivially an NFA Any language accepted by a DFA is also accepted by an NFA 74

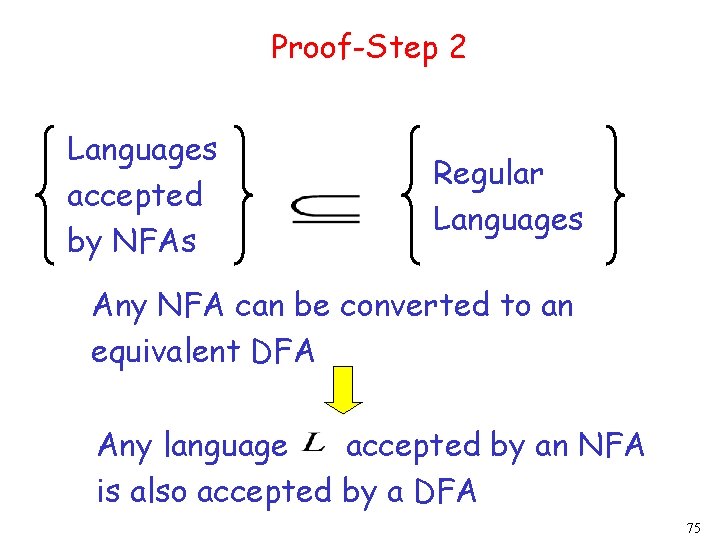
Proof-Step 2 Languages accepted by NFAs Regular Languages Any NFA can be converted to an equivalent DFA Any language accepted by an NFA is also accepted by a DFA 75

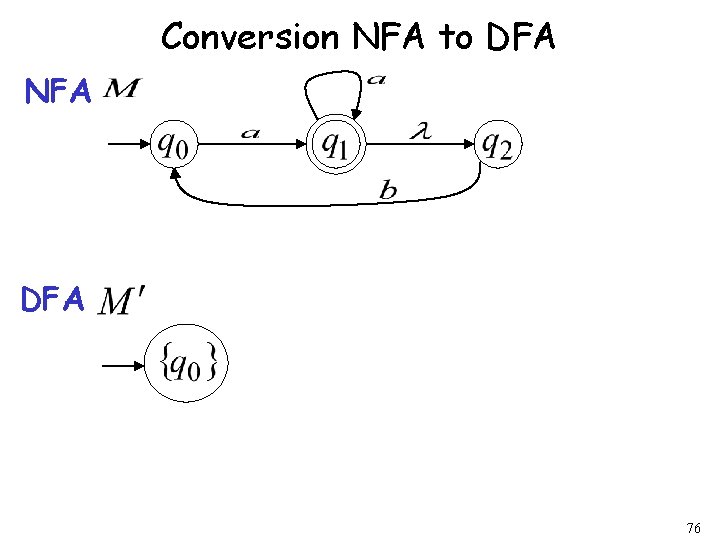
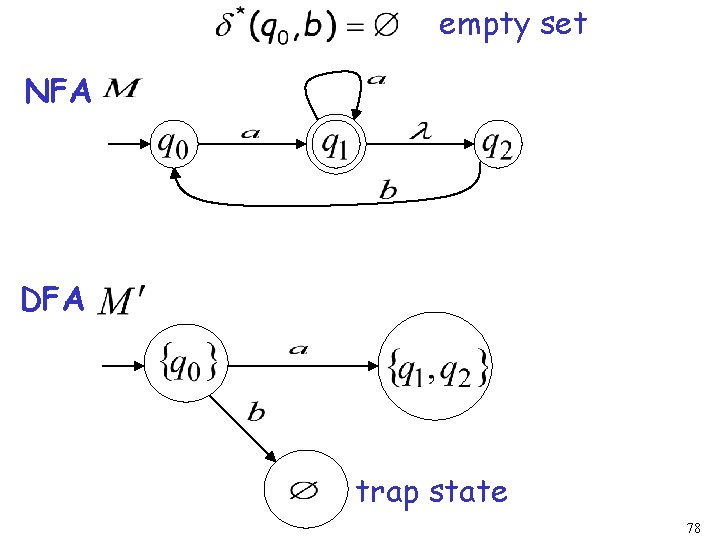
Conversion NFA to DFA NFA DFA 76

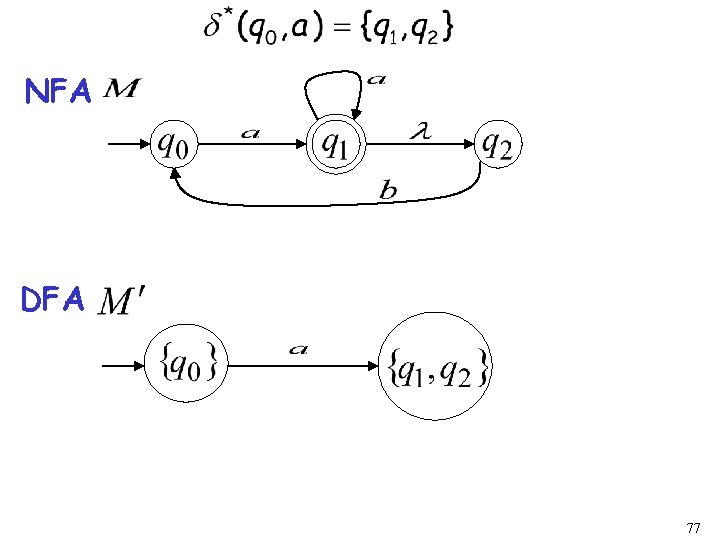
NFA DFA 77

empty set NFA DFA trap state 78

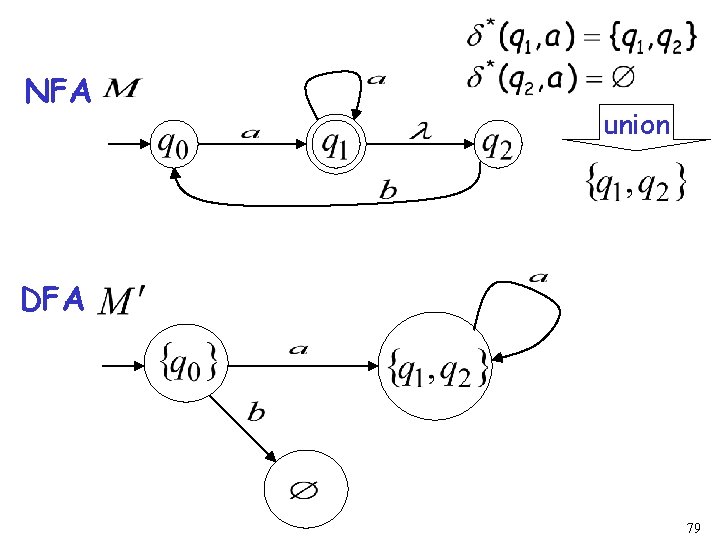
NFA union DFA 79

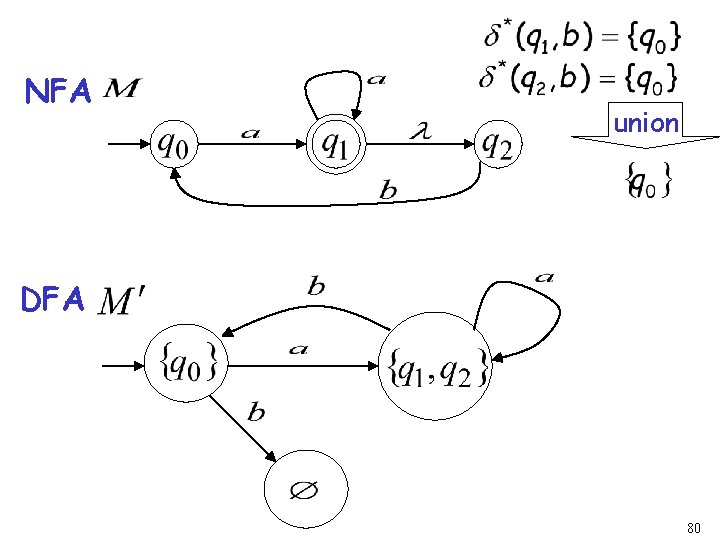
NFA union DFA 80

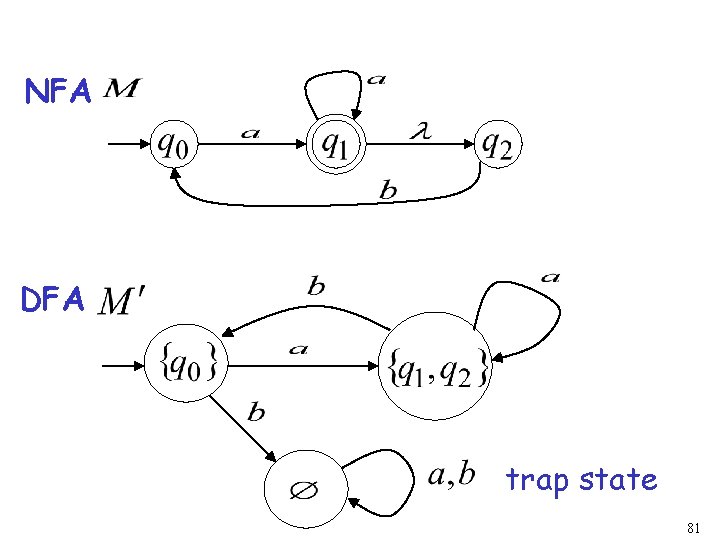
NFA DFA trap state 81

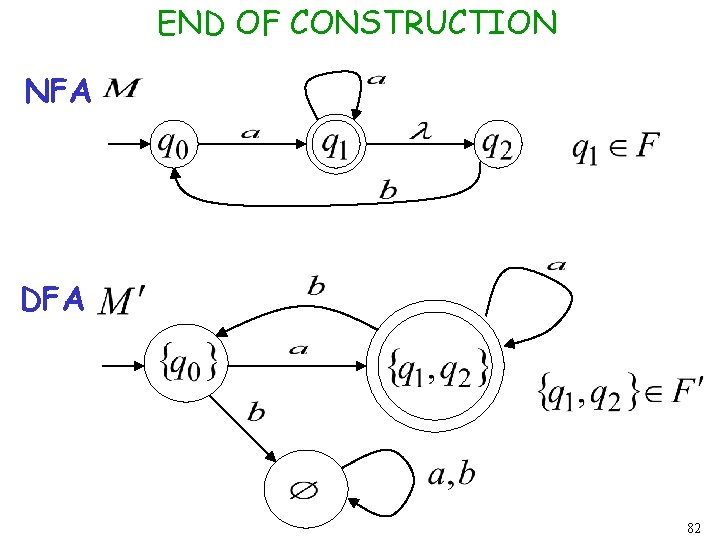
END OF CONSTRUCTION NFA DFA 82

General Conversion Procedure Input: an NFA Output: an equivalent DFA with 83

The NFA has states The DFA has states from the power set 84

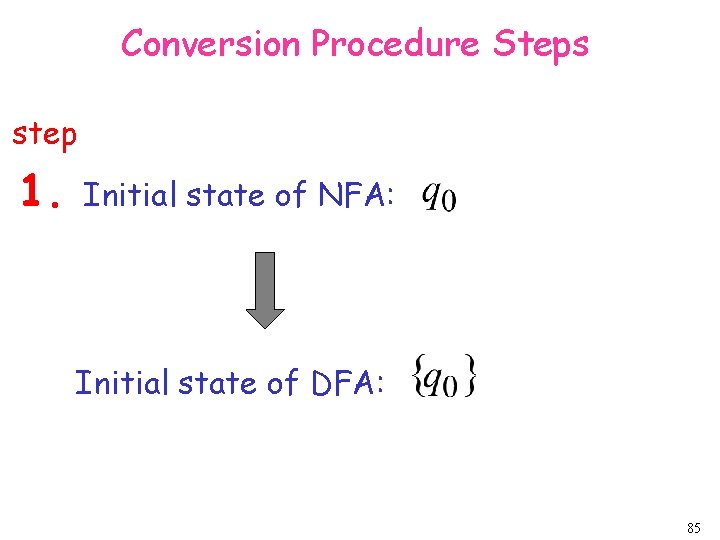
Conversion Procedure Steps step 1. Initial state of NFA: Initial state of DFA: 85

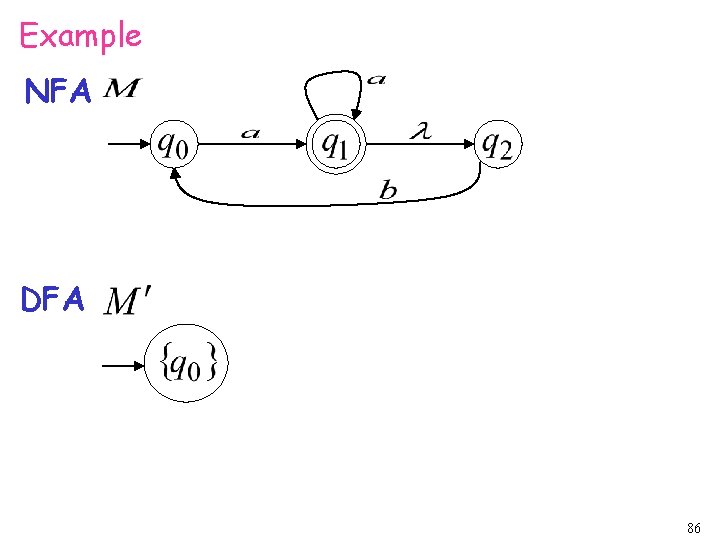
Example NFA DFA 86

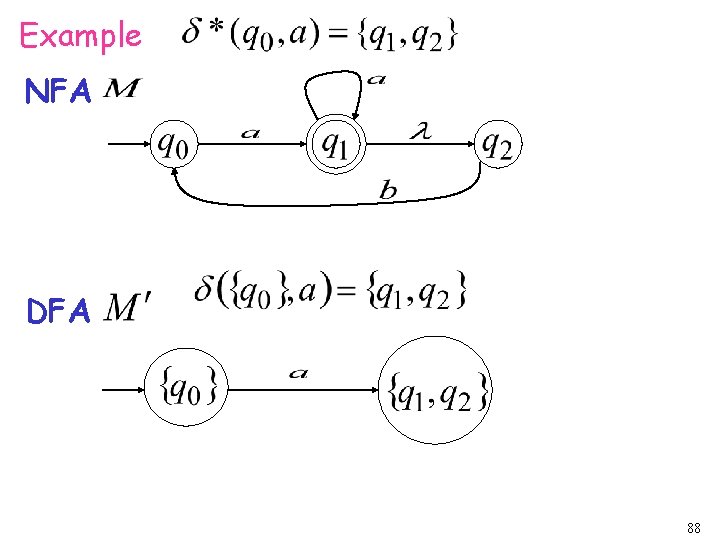
step 2. For every DFA’s state compute in the NFA Union add transition to DFA 87

Example NFA DFA 88

step 3. Repeat Step 2 for every state in DFA and symbols in alphabet until no more states can be added in the DFA 89

Example NFA DFA 90

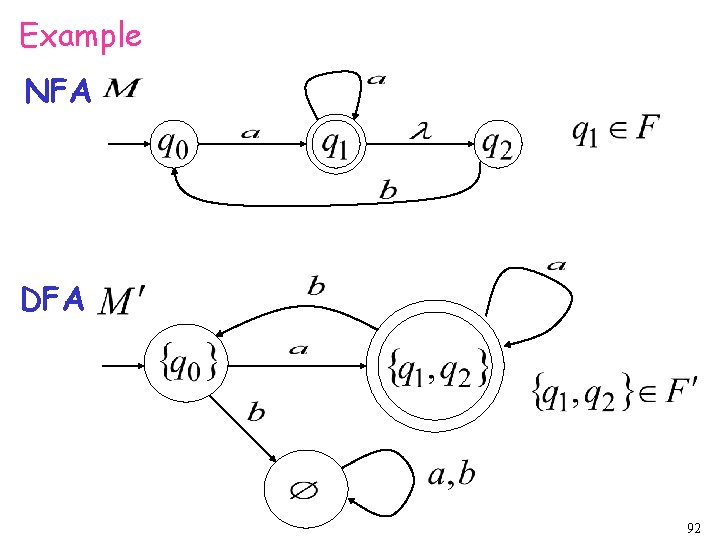
step 4. For any DFA state if some is accepting state in NFA Then, is accepting state in DFA 91

Example NFA DFA 92

Lemma: If we convert NFA to DFA then the two automata are equivalent: Proof: We only need to show: AND 93
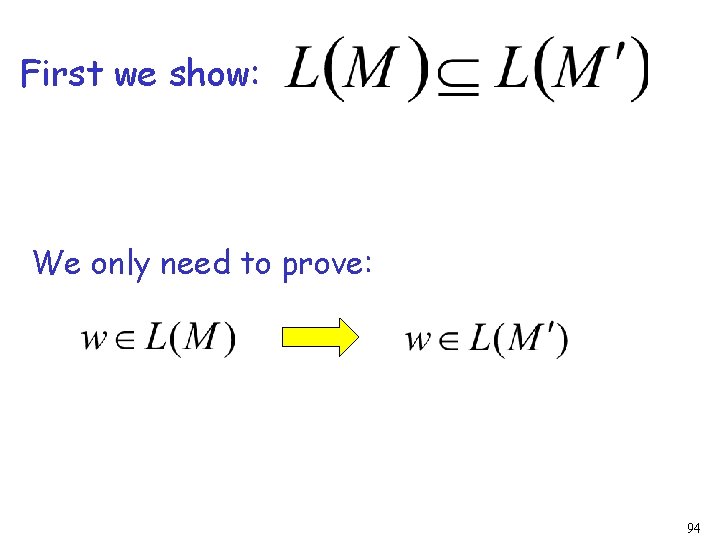
First we show: We only need to prove: 94

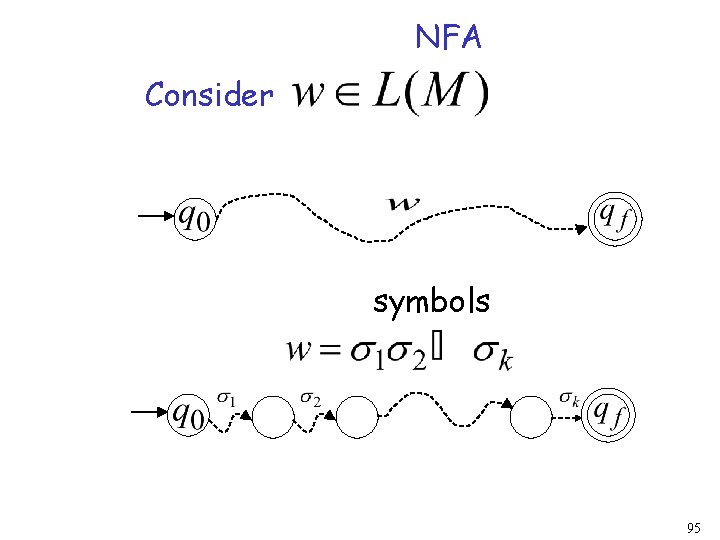
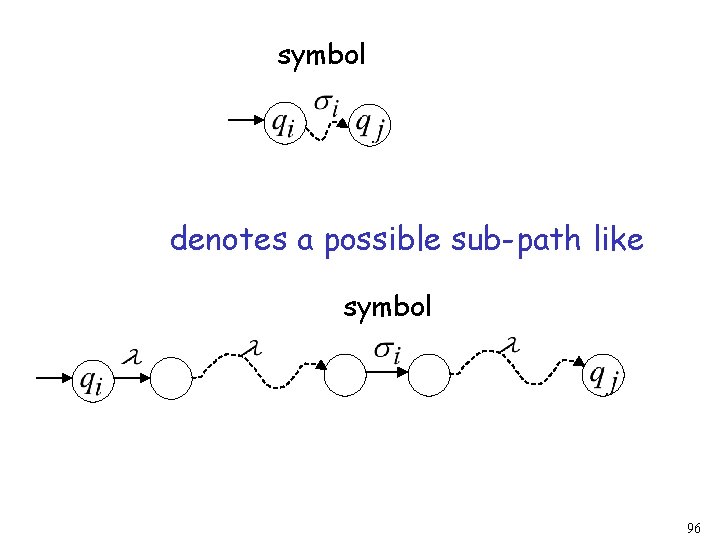
NFA Consider symbols 95

symbol denotes a possible sub-path like symbol 96

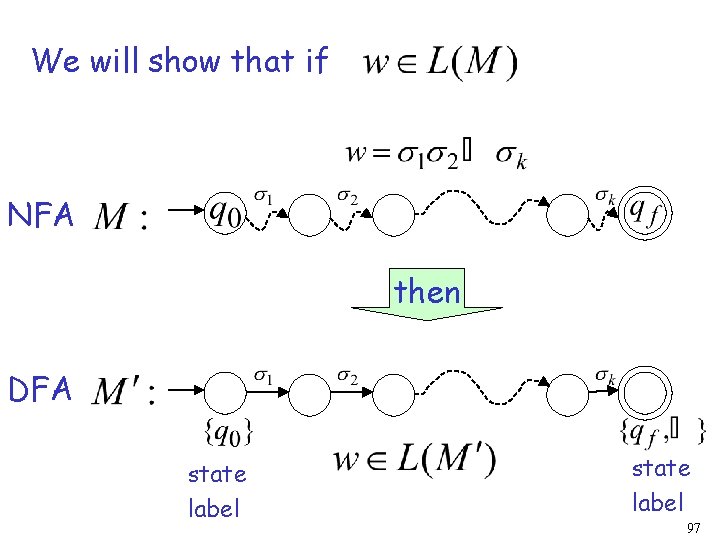
We will show that if NFA then DFA state label 97

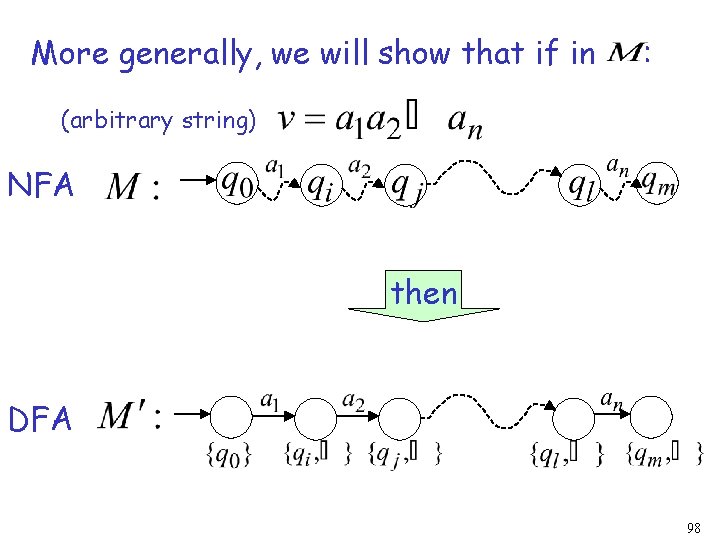
More generally, we will show that if in : (arbitrary string) NFA then DFA 98

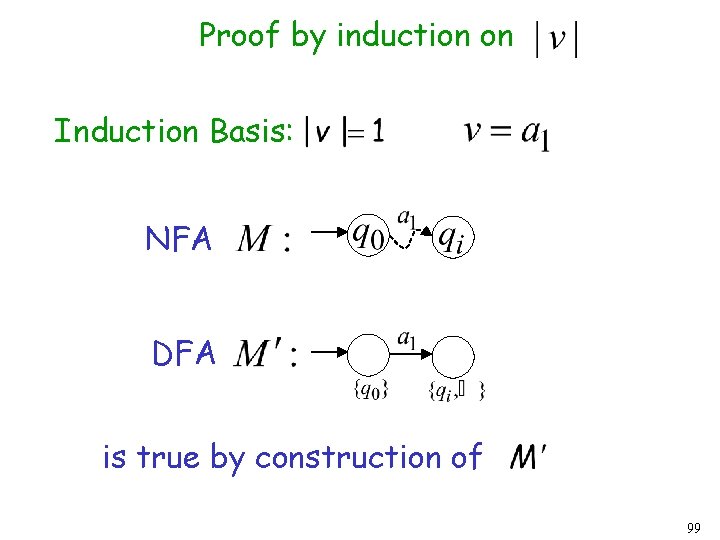
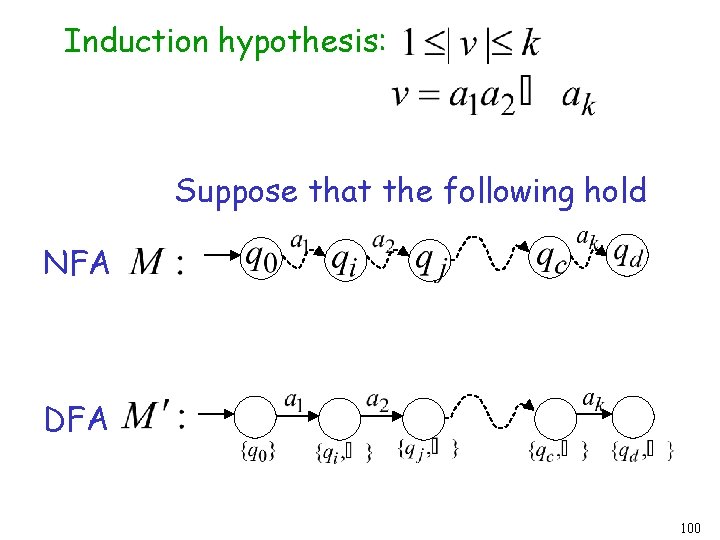
Proof by induction on Induction Basis: NFA DFA is true by construction of 99

Induction hypothesis: Suppose that the following hold NFA DFA 100

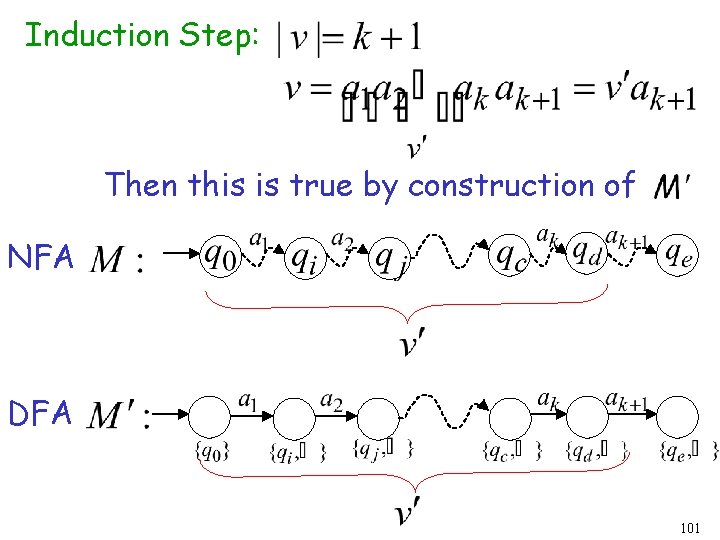
Induction Step: Then this is true by construction of NFA DFA 101

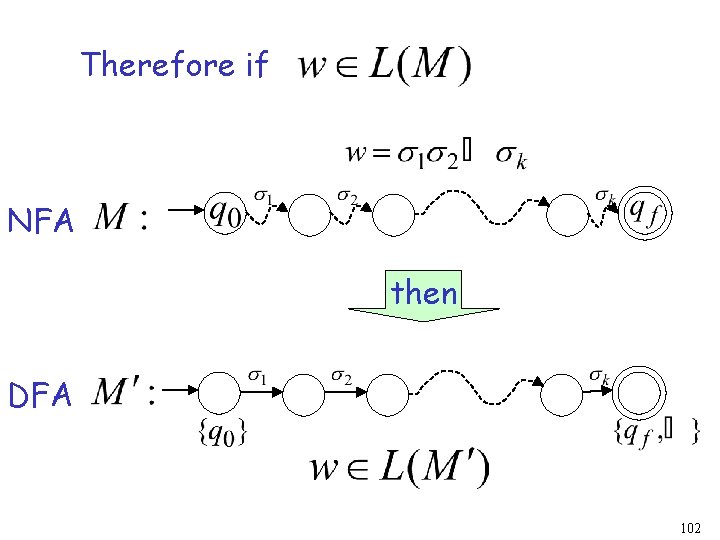
Therefore if NFA then DFA 102

We have shown: With a similar proof we can show: Therefore: END OF LEMMA PROOF 103

ﺍﻟﻤﻤﻠﻜﺔ ﺍﻟﻌﺮﺑﻴﺔ ﺍﻟﺴﻌﻮﺩﻳﺔ ﻭﺯﺍﺭﺓ ﺍﻟﺘﻌﻠﻴﻢ ﺟﺎﻣﻌﺔ ﺃﻢ ﺍﻟﻘﺮﻯ ﺍﻟﻜﻠﻴﺔ ﺍﻟﺠﺎﻣﻌﻴﺔ ﺃﻀﻢ ﻗﺴﻢ ﺍﻟﺤﺎﺳﺐ ﺍﻵﻠﻲ Kingdom of Saudi Arabia Ministry of Education Umm Al. Qura University Adam University College Computer Science Department This Summary is an Online Content from this Book: Michael Sipser, Introduction to the Theory of Computation, 2 nd. Edition It is edited for Computation Theory Course 68034153 by: T. Mariah Sami Khayat Teacher Assistant @ Adam University College For Contacting: mskhayat@uqu. edu. sa 104