Nonconvex Rigid Bodies with Stacking Eran Guendelman Robert

Nonconvex Rigid Bodies with Stacking Eran Guendelman Robert Bridson Ron Fedkiw Stanford University

Paper Overview Goal: • Plausible simulation of a large number of nonconvex rigid bodies. • Handle collision, contact, friction, stacking.

Main Contributions • A new time stepping scheme. • A “shock propagation” technique for stacks.

Geometric Representation • A dual representation. • Explicit: Triangulated surface. – Supplies point samples on surface. • Implicit: Signed distance function Φ. – Φ distance to surface, Φ < 0 inside, Φ > 0 outside. – Stored on a uniform or octree grid. – Constant time inside/outside test. – Normal = Φ (defined throughout space).

Time Stepping: Traditional Approach • Traditional time stepping simulation loop: – Update position and velocity. – Process collision. – Process contact.

Problem With Traditional Approach • Problem: e. g. Block sliding down inclined plane. – Initially sliding down. – Update position and velocity interpenetrating plane. – Process collision velocity reflected. – No contact to process. – Next iteration object bounces.

Fixing Problem • Velocity threshold. – e. g. [Mirtich & Canny ’ 95 – 2 papers] – Process as contact if speed below threshold. • Our approach doesn’t require such threshold.

Time Stepping: Our Approach • A new ordering of the simulation loop: – Process collision. Recall traditional approach: – Update velocity. • Update pos & vel. – Process contact. • Process collision. – Update position. • Process contact. • Some justification: – Velocity update integrates forces and contact processing resolves forces.

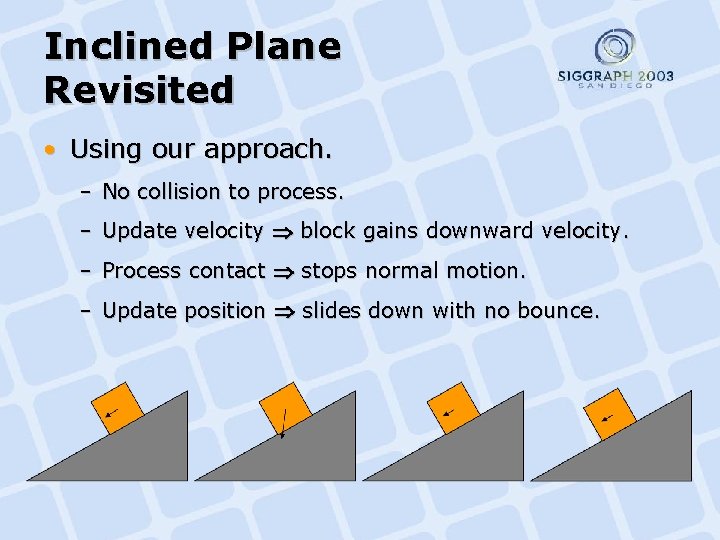
Inclined Plane Revisited • Using our approach. – No collision to process. – Update velocity block gains downward velocity. – Process contact stops normal motion. – Update position slides down with no bounce.

TIME STEPPING COMPARISON

Time Stepping Comparison • Errors accentuated: – Perfectly elastic collisions (ε=1). – We don’t rewind to collision time. – Impulses applied sequentially at point samples.

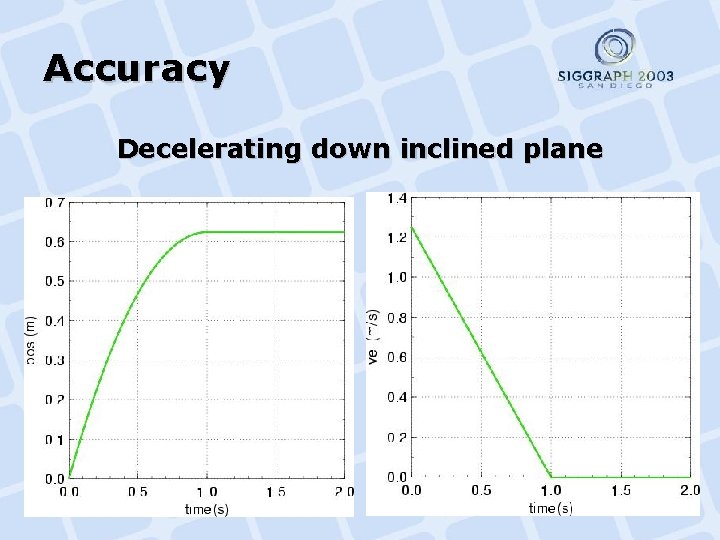
Accuracy Decelerating down inclined plane

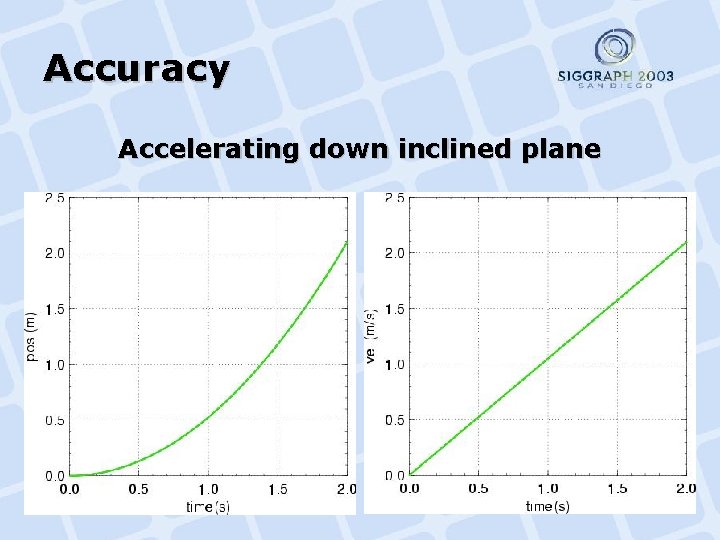
Accuracy Accelerating down inclined plane

Simulation Step • Choose sufficiently small time step ∆t. • Advance bodies using time stepping scheme. – Use forward Euler for position and velocity update. • Doesn’t guarantee non-interpenetration, but achieves good results. – Experimented with “pushing out” to reduce penetration as in [Baraff ‘ 95].

Interference Detection • We don’t rewind to collision time. • Find all penetrating vertices. – Use implicit surface inside/outside test. • Optionally compute edge-face intersections. • Accelerations: – Uniform spatial partition. – Bounding boxes.

Impulse • Impulses are used for collision and contact. • Collision parameters: ε and μ. • Collision normal = Φ. • Use Coulomb friction model: – Compute impulse to stop tangential motion. – If outside friction cone, find kinetic friction impulse. – Similar to [Hahn ‘ 88; Moore & Wilhelms ‘ 88]. • Rolling and spinning friction.

Collision Processing • Detect and resolve collisions during time step. • One approach: Process in chronological order. – Computationally expensive for scenes with frequent collisions. • Approach we use: Process all at end of step. – Gives plausible results. – Don’t need to rewind to exact time of collision.

Collision Processing: Algorithm Overview • Compute candidate positions of bodies. • For each intersecting pair of bodies: – Determine interpenetrating points. – Sort points by penetration depth (deepest first). – For each point in order: • Apply frictional impulse (unless bodies receding).

Collision Processing: Algorithm Overview • Repeat above a number of times. – Resolving one collision might create new ones. • Applies series of impulses rather than simultaneously resolving all collisions.

Contact Processing • Determine contacts and prevent penetration. • Approaches: – Simultaneously solve for all contact forces. – Penalty method (repulsion forces). e. g. [Baraff ‘ 94] e. g. [Moore & Wilhelms ‘ 88] • Approach we use: – Approximate continuous contact by a series of inelastic impulses. e. g. [Mirtich & Canny ‘ 95] – Algorithm similar to collision processing (with ε=0), but modified for improved accuracy.

Improving Accuracy • Gradually slow down bodies. – Transition impulses from ε=-1 to ε=0. – -1<ε<0: Slows normal approach velocity. – Use more (smaller) impulses for contact. • Compute impulses in old position. – Still use candidate position to find contact points. OLD CANDIDATE

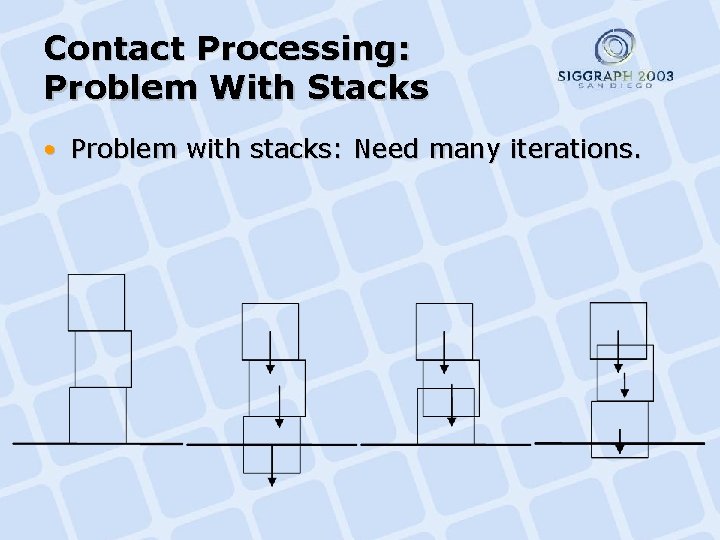
Contact Processing: Problem With Stacks • Problem with stacks: Need many iterations.

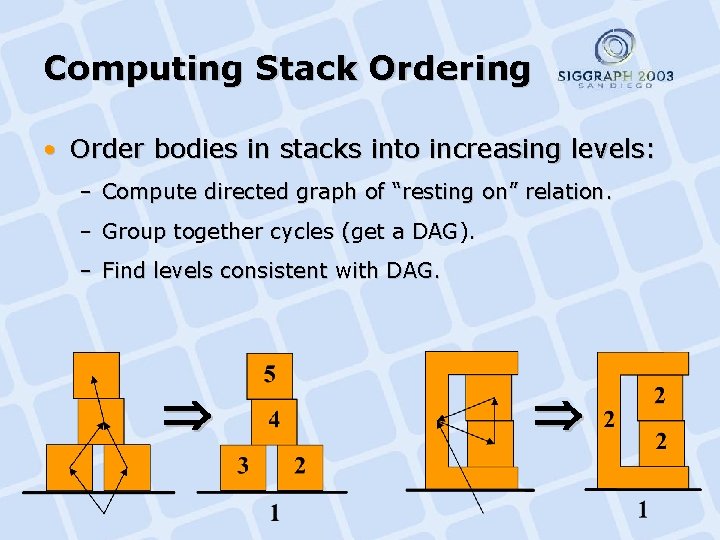
Computing Stack Ordering • Order bodies in stacks into increasing levels: – Compute directed graph of “resting on” relation. – Group together cycles (get a DAG). – Find levels consistent with DAG.

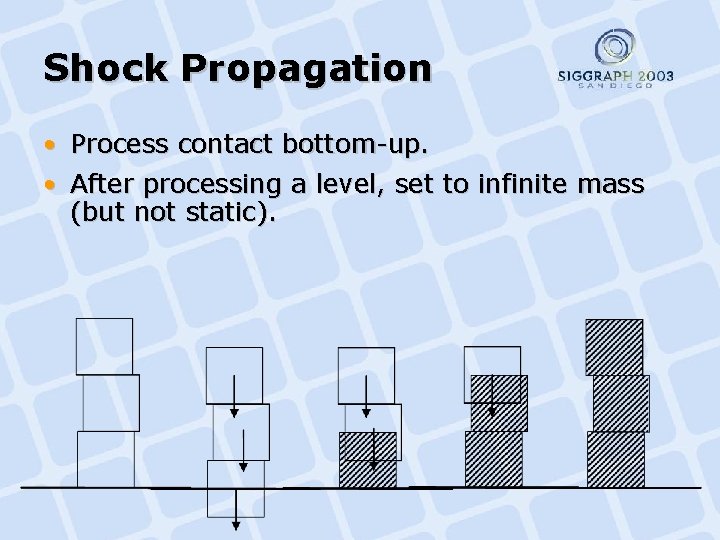
Shock Propagation • Process contact bottom-up. • After processing a level, set to infinite mass (but not static).

SHOCK PROPAGATION ONLY

Combining Contact and Shock Propagation • Run a number of regular contact iterations. – Without setting levels to infinite mass. – Transmits weight through stack. • Run a single iteration of shock propagation. – Get good behavior without requiring many iterations.

CONTACT & SHOCK PROPAGATION

SHOCK PROPAGATION ONLY

CONTACT & SHOCK PROPAGATION

Summary • Dual representation of geometry. • Impulse-based simulator. • New time stepping approach eliminates need for a velocity threshold. • Shock propagation shocks the stack into a reasonable configuration without requiring many contact iterations.