Noncompact Hopf Maps Quantum Hall Effect and Twistor

Non-compact Hopf Maps, Quantum Hall Effect, and Twistor Theory Graduate School of Mathematics, Nagoya University, 23 Jul. 2009 Kazuki Hasebe Takuma N. C. T. ar. Xiv: 0902. 2523, 0905. 2792 Takuma N. C. T.

Introduction 1. Twistor Theory (Mathematical Physics: Relativistic Quantum Mechanics) Quantization of Space-Time Light has special importance. R. Penrose (1967) ADHM Construction, Integrable Models. Twistor String etc. 2. Quatum Hall Effect (Condensed matter: Non-relativistic Quantum Mechanics) Novel Quantum State of Matter Monopole plays an important role. R. Laughlin (1983) Quatum Spin Hall Effect, Quantum Hall Effect in Graphene etc. There are remarkable close relations between these two independently developed fields !

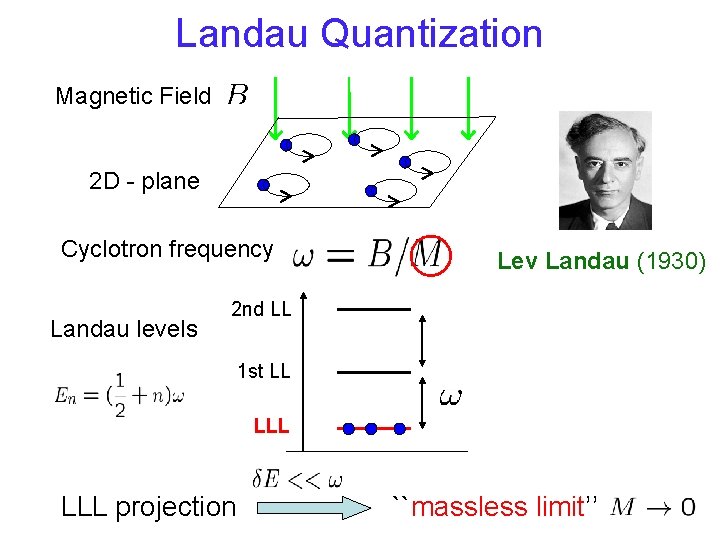
Landau Quantization Magnetic Field 2 D - plane Cyclotron frequency Landau levels Lev Landau (1930) 2 nd LL 1 st LL LLL projection ``massless limit’’

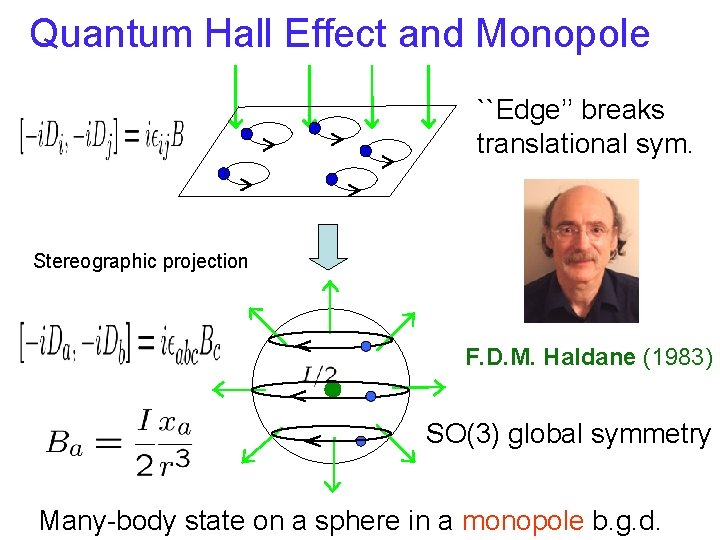
Quantum Hall Effect and Monopole ``Edge’’ breaks translational sym. Stereographic projection F. D. M. Haldane (1983) SO(3) global symmetry Many-body state on a sphere in a monopole b. g. d.

Heuristic Observation: Why Light & Monopole Massless particle with helicity spin momentum The position of a massless particle with definite helicity is uncertain ! If To satisfy the SU(2) algebra Bacry (1981) Atre, Balachandran, Govindarajan (1986) Massless particle ``sees’’ a charge monopole in p-space !

Brief Introduction to Twistor

Twistor Program Roger Penrose (1967) Quantization of Space-Time What is the fundamental variables ? Light (massless-paticle) will play the role ! Space-Time Twistor Space ``moduli space of light’’

Massless Free Particle Free particle Massless particle : Gauge symmetry

Twistor Description : Incidence Relation Helicity: Massless limit Fundamental variable Suggests a fuzzy space-time.

Hopf Maps and QHE

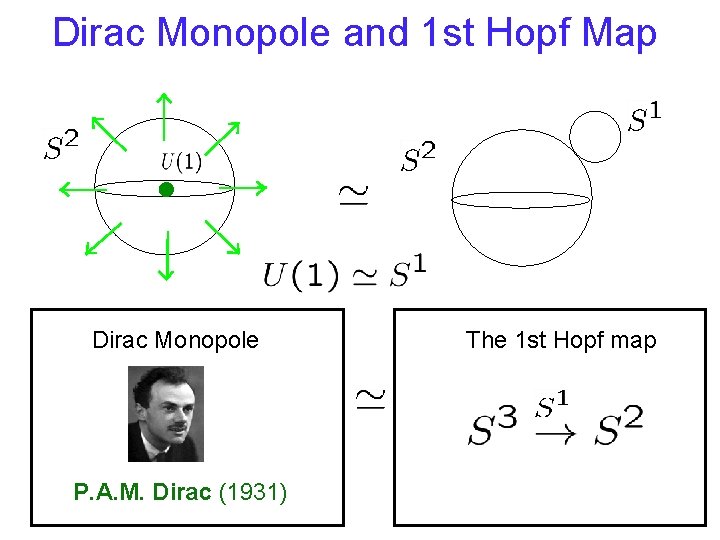
Dirac Monopole and 1 st Hopf Map Dirac Monopole P. A. M. Dirac (1931) The 1 st Hopf map

Explicit Realization of 1 st Hopf Map Hopf spinor Connection of bundle

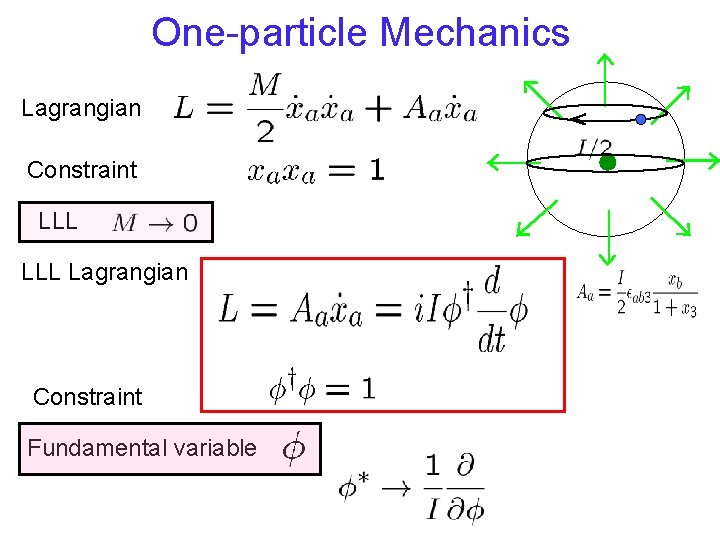
One-particle Mechanics Lagrangian Constraint LLL Lagrangian Constraint Fundamental variable

LLL Physics Emergence of Fuzzy Geometry Holomorphic wavefunctions

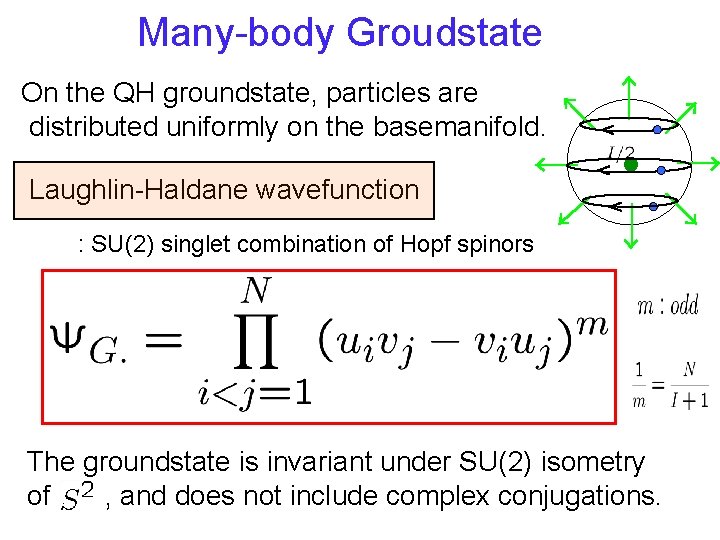
Many-body Groudstate On the QH groundstate, particles are distributed uniformly on the basemanifold. Laughlin-Haldane wavefunction : SU(2) singlet combination of Hopf spinors The groundstate is invariant under SU(2) isometry of , and does not include complex conjugations.

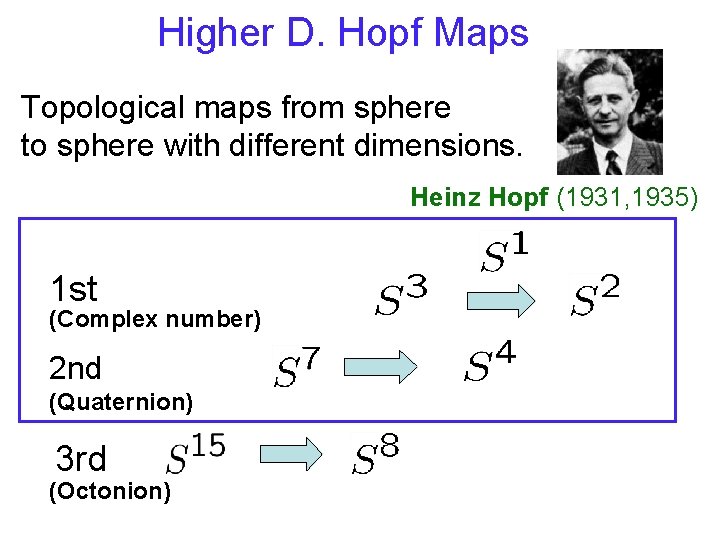
Higher D. Hopf Maps Topological maps from sphere to sphere with different dimensions. Heinz Hopf (1931, 1935) 1 st (Complex number) 2 nd (Quaternion) 3 rd (Octonion)

Quaternion and 2 nd Hopf Map C 1 st Hopf map Unit C 2 nd Hopf map Unit Quaternion Willian R. Hamilton (1843)

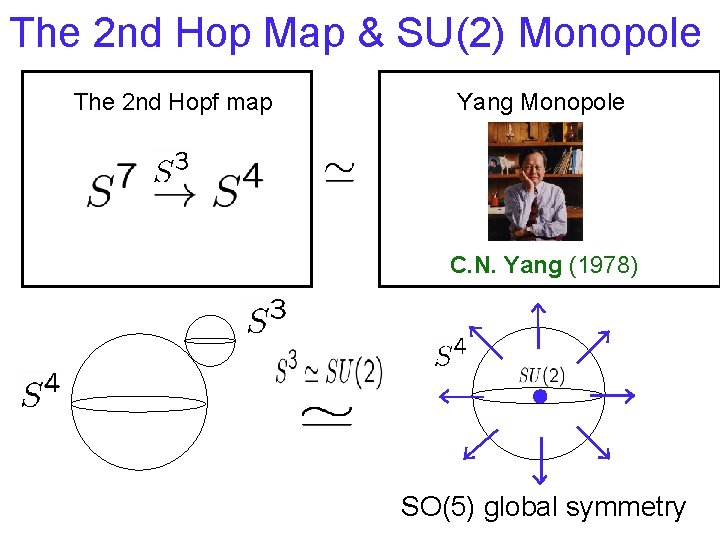
The 2 nd Hop Map & SU(2) Monopole The 2 nd Hopf map Yang Monopole C. N. Yang (1978) SO(5) global symmetry

4 D QHE and Twistor Many-body problem on a foursphere in a SU(2) monopole b. g. d. In the LLL S. C. Zhang, J. P. Hu (2001) Point out relations to Twistor theory D. Karabali, V. P. Nair (2002, 2003) S. C. Zhang (2002) In particular, Sparling and his coworkers suggested the use of the ultra-hyperboloid G. Sparling (2002) D. Mihai, G. Sparling, P. Tillman (2004)

Short Summary QHE Hopf Map Division algebra 2 D 1 st 4 D 2 nd complex numbers quaternions LLL Twistor ? ? 8 D 3 rd octonions

QHE with SU(2, 2) symmetry

Noncompact Version of the Hopf Map Hopf maps Non-compact groups Complex number Non-compact Hopf maps ! James Cockle (1848, 49) Split-Complex number Quaternions Split-Quaternions Octonions Split-Octonions

Split-Algebras Split-Complex number Split-Quaternions

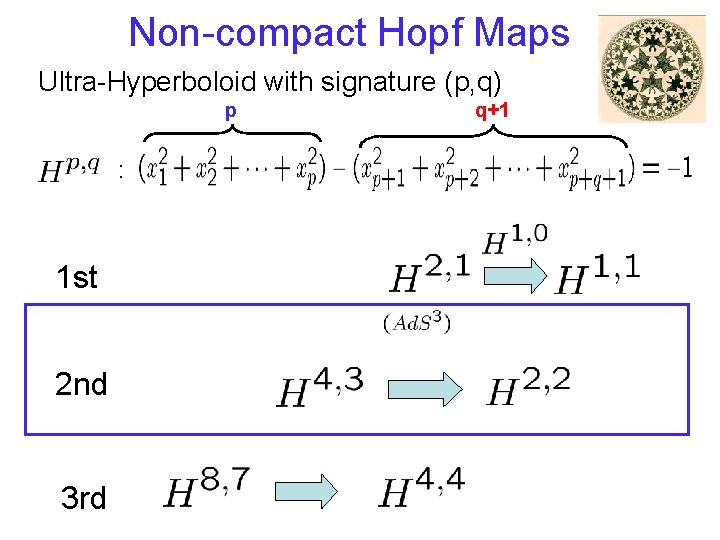
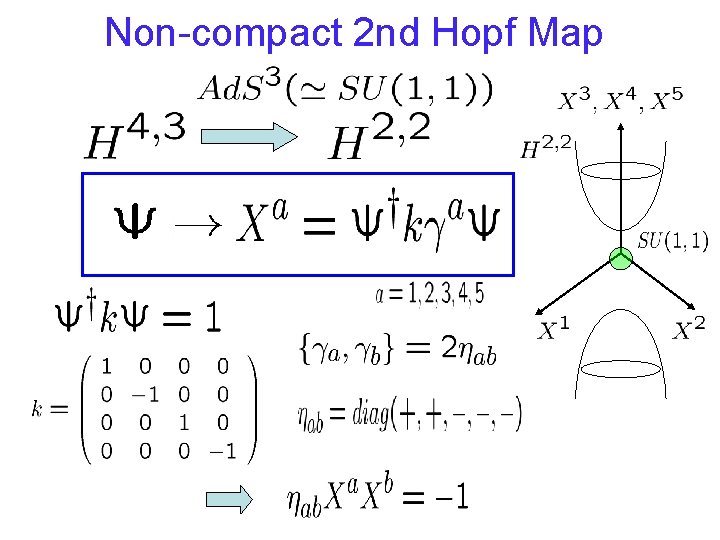
Non-compact Hopf Maps Ultra-Hyperboloid with signature (p, q) p : 1 st 2 nd 3 rd q+1

Non-compact 2 nd Hopf Map

SO(3, 2) Hopf spinor generators Incidence Relation Stereographic coordinates

One-particle Mechanics on Hyperboloid SU(1, 1) monopole One-particle action constraint SO(3, 2) symmetry (c. f. )

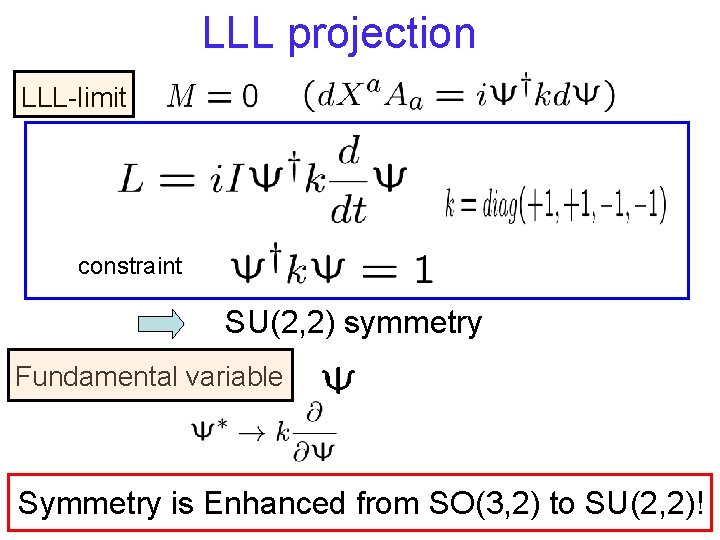
LLL projection LLL-limit constraint SU(2, 2) symmetry Fundamental variable Symmetry is Enhanced from SO(3, 2) to SU(2, 2)!

Realization of the fuzzy geometry First, the Hopf spinor space becomes fuzzy. Then, the hyperboloid also becomes fuzzy. The space(-time) non-commutativity comes out from that of the more fundamental space. This demonstrates the philosophy of Twistor !

Analogies QHE Twistor l Massless Condition SU(2, 2) Enhanced Symmetry l More Fundamental Quantity than Space-Time Quantize and rather than ! l Complex conjugation = Derivative Noncommutative Geometry, Holomorphic functions

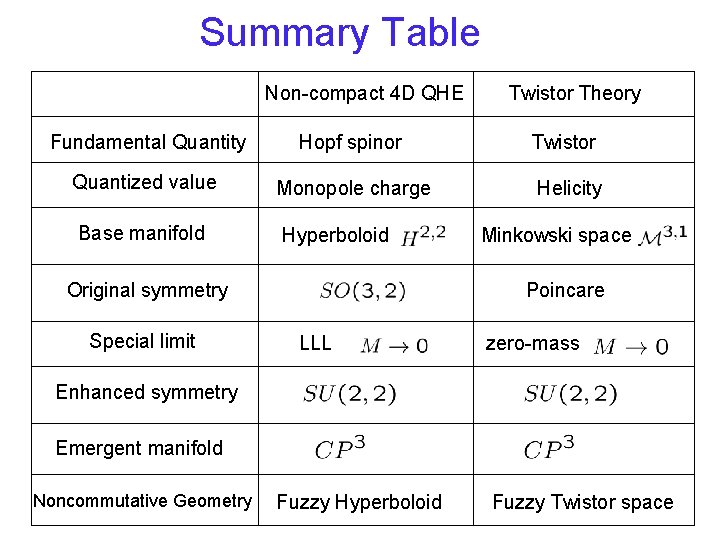
Summary Table Non-compact 4 D QHE Twistor Theory Fundamental Quantity Hopf spinor Twistor Quantized value Monopole charge Helicity Base manifold Hyperboloid Original symmetry Special limit Minkowski space Poincare LLL zero-mass Enhanced symmetry Emergent manifold Noncommutative Geometry Fuzzy Hyperboloid Fuzzy Twistor space

Physics of the non-compact 4 D QHE

One-particle Problem Landau problem on a ultra-hyperboloid Thermodynamic limit : fixed

Many-body Groudstate On the QH groundstate, particles are distributed uniformly on the basemanifold. Laughlin-Haldane wavefunction The groundstate is invariant under SO(3, 2) isometry of , and does not include complex conjugations.

Topological Excitations l Topological excitations are generated by flux penetrations. l The flux has SU(1, 1) internal structures. Membrane-like excitations !

Perspectives

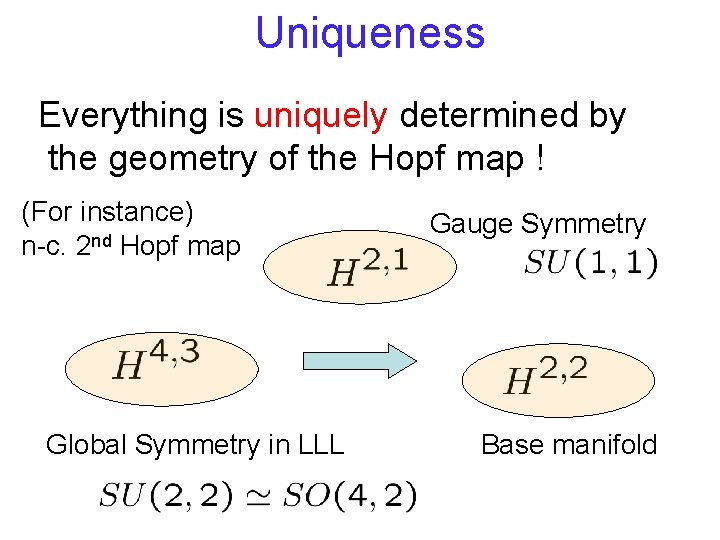
Uniqueness Everything is uniquely determined by the geometry of the Hopf map ! (For instance) n-c. 2 nd Hopf map Global Symmetry in LLL Gauge Symmetry Base manifold

Extra-Time Physics ? Base manifold 2 T Gauge Symmetry l This set-up exactly corresponds to 2 T physics developed by I. Bars ! l Sp(2, R) gauge symmetry is required to eliminate the negative norms. l The present model fulfills this requirement from the very beginning ! l There may be some kind of ``duality’’ ? ? C. M. Hull (99)

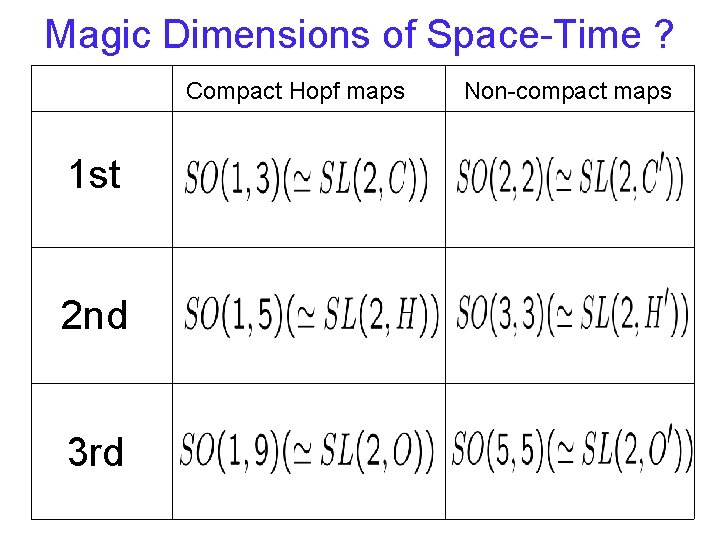
Magic Dimensions of Space-Time ? Compact Hopf maps 1 st 2 nd 3 rd Non-compact maps

After ALL Split-algebras Non-compact Hopf Maps Higher D. quantum liquid Membrane-like excitation Non-commutative Geometry Twistor Theory Uniqueness Extra-time physics Magic Dimensions

Deep mathematical structure exists behind the model ! Entire picture is still Mystery ! END