Noncoding RNA Identification Using Heuristic Methods ICS 690

Non-coding RNA Identification Using Heuristic Methods ICS 690 – Seminar MSc. Jonas Krause Dr. Guylaine Poisson Dr. Kyungim Baek

Agenda Heuristic Methods • Differential Evolution (DE) • Binary Differential Evolution (BDE) • Discretized Differential Evolution (DDE) • Others (GA, PSO, ABC, etc. ) Problem and Mathematical Model • Binary Variables • Linear Mathematical Model Objectives • Apply BDE to the existing Linear Math Model • Apply DDE to an improved Linear Math Model • Develop a Non-linear Math Model and apply DE and Non-linear Math Programming (NLP) Slide 2

Heuristic Methods • In computer science and mathematical optimization, heuristic is a technique designed for solving problems more quickly when classic methods are too slow (ex. MILP) • Alternative methods for problems with gigantic search spaces (high number of variables and restrictions) • Parameter based algorithms: Population, Generations, Mutation and Crossover • Heuristic methods do not guarantee the optimal solution Slide 3

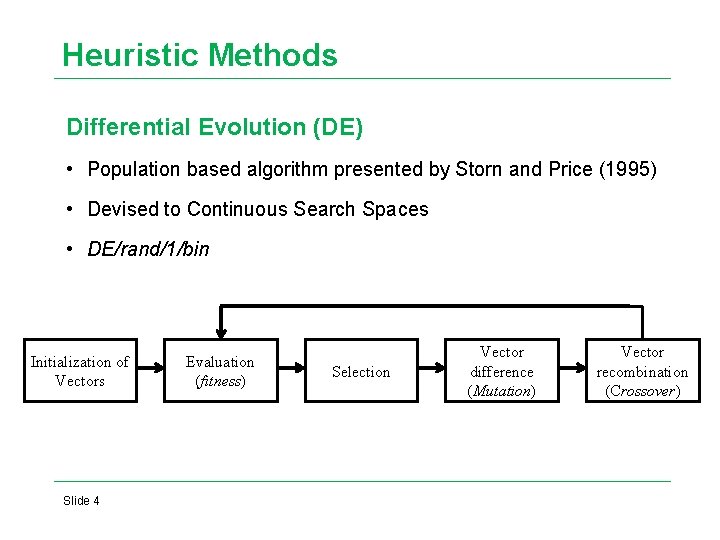
Heuristic Methods Differential Evolution (DE) • Population based algorithm presented by Storn and Price (1995) • Devised to Continuous Search Spaces • DE/rand/1/bin Initialization of Vectors Slide 4 Evaluation (fitness) Selection Vector difference (Mutation) Vector recombination (Crossover)

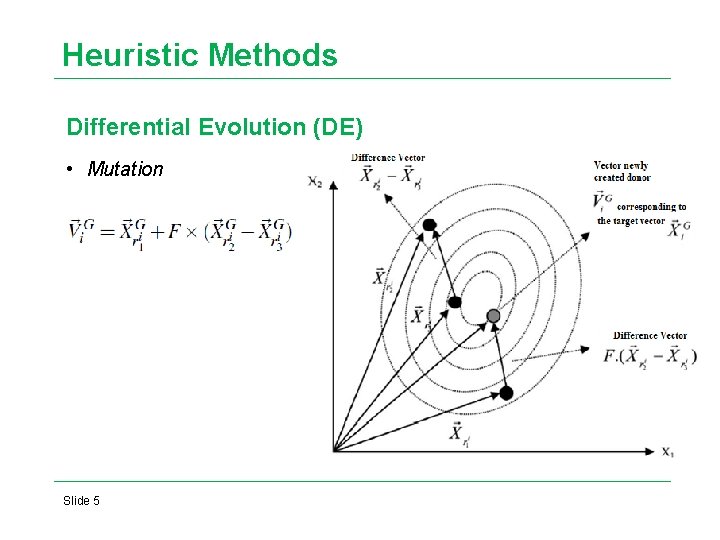
Heuristic Methods Differential Evolution (DE) • Mutation Slide 5

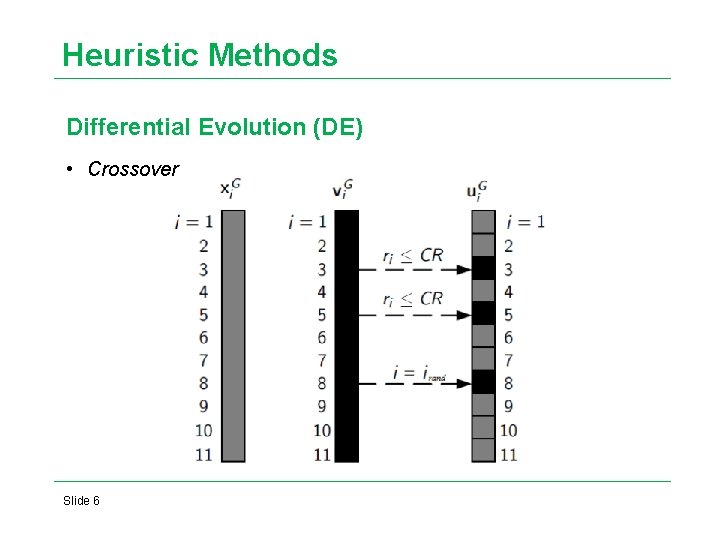
Heuristic Methods Differential Evolution (DE) • Crossover Slide 6

Heuristic Methods Binary Differential Evolution (BDE) • Algorithm inspired by the standard DE and the mutation process GA Slide 7

Heuristic Methods Discretized Differential Evolution (DDE) • Standard DE Mutation and Crossover processes • Each dimension of the individual is discretized by the sigmoid function Slide 8

Heuristic Methods Implemented in: • Knapsack Problem - KRAUSE, Jonas; Parpinelli, R. S. ; Lopes, H. S. Proposta de um algoritmo inspirado em Evolução Diferencial aplicado ao Problema Multidimensional da Mochila, 2012, Curitiba. Anais do Encontro Nacional de Inteligência Artificial – ENIA. - KRAUSE, Jonas; Cordeiro, J. A. ; Lopes, H. S. . Comparação de Métodos de Computação Evolucionária para o Problema da Mochila Multidimensional. In: H. S. Lopes; L. C. A. Rodrigues; M. T. A. Steiner. (Org. ). Meta-Heurísticas em Pesquisa Operacional. 1 ed. Curitiba: Omnipax, 2013, p. 87 -98. - KRAUSE, Jonas; Lopes, H. S. A comparison of differential evolution algorithm with binary and continuous encoding for the MKP. In: BRICS - Conference on Computational Intelligence, 2014, Recife. Proceedings of BRICS-CCI, 2013. Slide 9

Heuristic Methods Implemented in: • Scheduling Problem - KRAUSE, Jonas; Sieczka, E. ; Lopes, H. S. Differential Evolution Variants and MILP for the Pipeline Network Schedule Optimization Problem. In: LA-CCI - Congress on Computational Intelligence, 2015, Curitiba. • Survey - KRAUSE, Jonas; Cordeiro, J. A. Parpinelli, R. S. ; Lopes, H. S. A Survey of Swarm Algorithms Applied to Discrete Optimization Problems. In: Xin-She Yang; Zhihua Cui; Renbin Xiao; Amir Hossein Gandomi; Mehmet Karamanoglu. (Org. ). Swarm Intelligence and Bio-inspired Computation. 1 ed. Amsterdam: Elsevier, 2013, p. 169 -191. Slide 10

Heuristic Methods Other heuristic algorithms: • • • Genetic Algorithm (GA) already implemented in bioinformatics' problems Particle Swarm Optimization (PSO) Artificial Bee Colony (ABC) Roach Infestation Optimization (RIO) Cuckoo Search Algorithm (CSA) Firefly Algorithm (FA) Gravitational Search Algorithm (GSA) Bat Algorithm (BA) Glow-worm Swarm Optimization Algorithm (GSO) Bacterial Evolutionary Algorithm (BEA) Invasive Weed Optimization (IWO) Slide 11

Problem and Mathematical Model nc. RNA Identification • Non-coding RNAs are functional RNA transcripts that do not translate into proteins; • Non protein-coding RNAs are currently a research hotspot in bioinformatics, recent discoveries have revealed new nc. RNA families performing several roles such as: Gene silencing, replication, gene expression regulation, transcriptions, chromosome stability, protein stability, translocation and RNA modification, processing and stability. Slide 12

Problem and Mathematical Model Example of nc. RNA data: Slide 13

Problem and Mathematical Model nc. RNA Identification • Ongoing research at Bioinformatics Laboratory (Bi. L-Manoa) • Dr. Guylaine Poisson and Dr. Kyungim Baek • Dr. Mark Menor proposed a Binary Mathematical Model and solved it using Binary Classification Methods • Menor, M. , Baek, K. , and Poisson, G. , Multiclass relevance units machine: Benchmark evaluation and application to small nc. RNA discovery. 2013, BMC Genomics, 14(Suppl 2): S 6, (extended version of the ISCB-Asia/SCCG 2012 proceeding. ) PMCID: PMC 3582431 • Menor, M. , Baek, K. , and Poisson, G. , Prediction of mature micro. RNA and piwi-interacting RNA without a genome reference or precursors. International Journal of Molecular Sciences, 16(1), pp. 1466 -1481, 2015. Slide 14

Objectives 1. Apply BDE to the existing binary model and compare its results/performance with the classification method used previously; 2. Understand problem’s characteristics and improve binary mathematical model proposed by Dr. Mark Menor, apply DDE to the improved math model and compare its results/performance; 3. (Main Objective) Propose a continuous and non-linear mathematical model for the problem. Apply DE as heuristic method and Non-Linear Math Programming as deterministic method. Slide 15

Objectives Expectations: • BDE, DDE and DE were successfully implemented in NPcomplete problems. Therefore, good initial results are expected; • A continuous and non-linear mathematical model can provide more realistic results when applied to biological problems. Slide 16

Thank you!!! Questions? Slide 17