Non Deterministic Automata 1 Nondeterministic Finite Accepter NFA




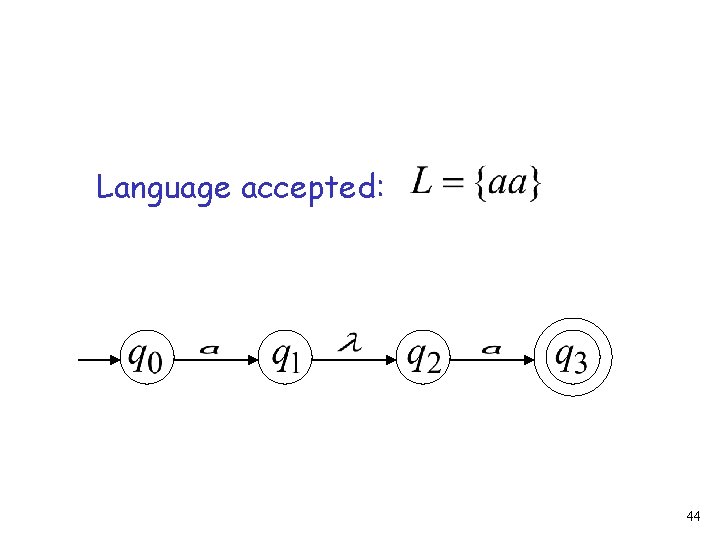












- Slides: 109

Non Deterministic Automata 1

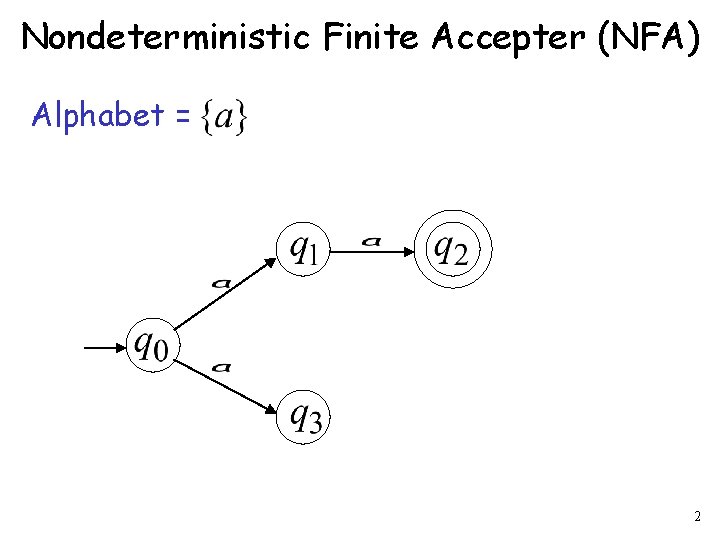
Nondeterministic Finite Accepter (NFA) Alphabet = 2

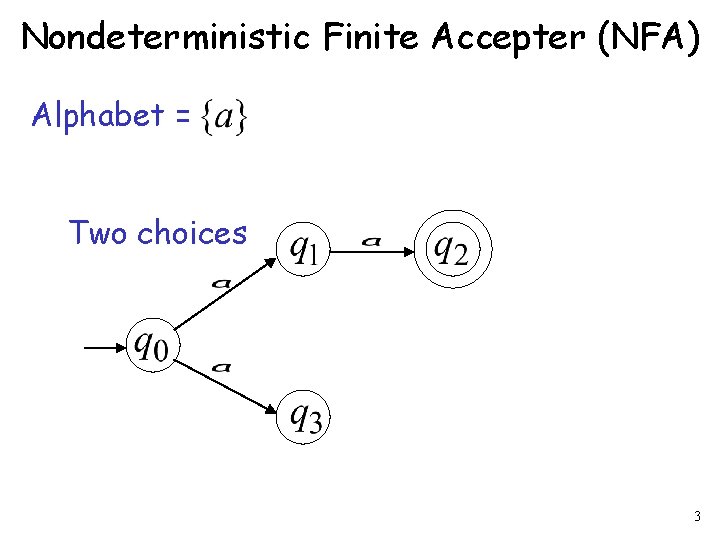
Nondeterministic Finite Accepter (NFA) Alphabet = Two choices 3

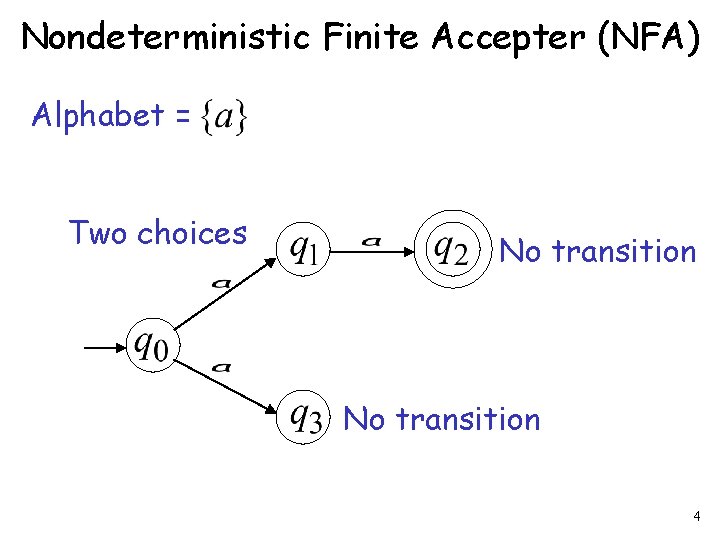
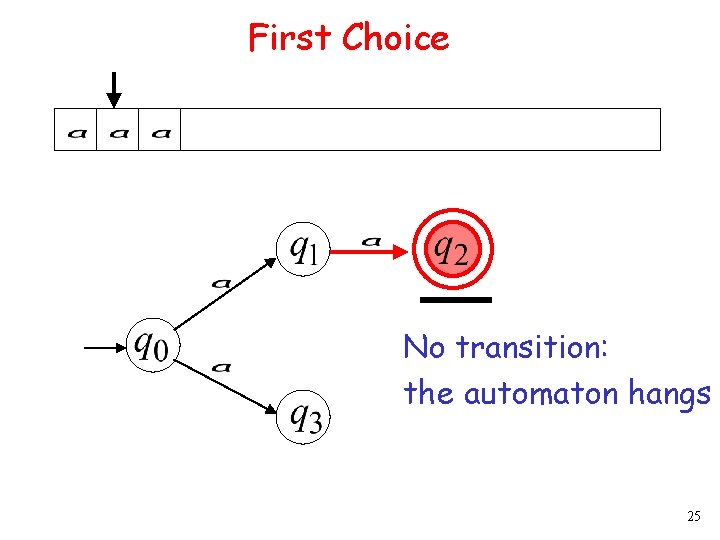
Nondeterministic Finite Accepter (NFA) Alphabet = Two choices No transition 4

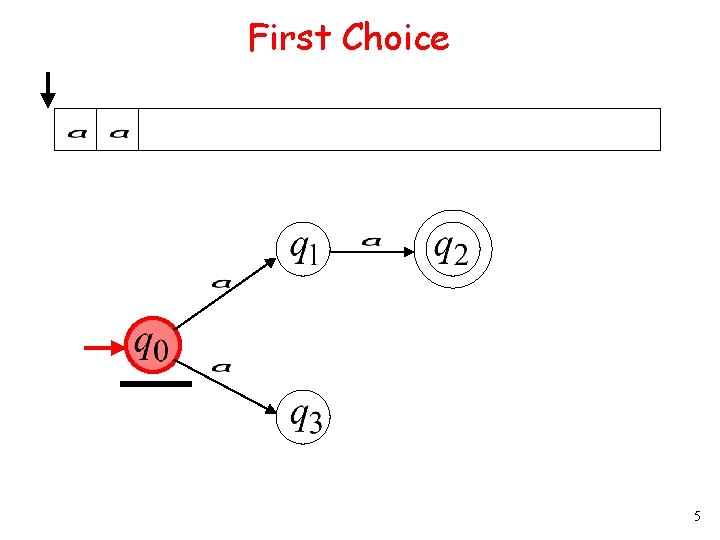
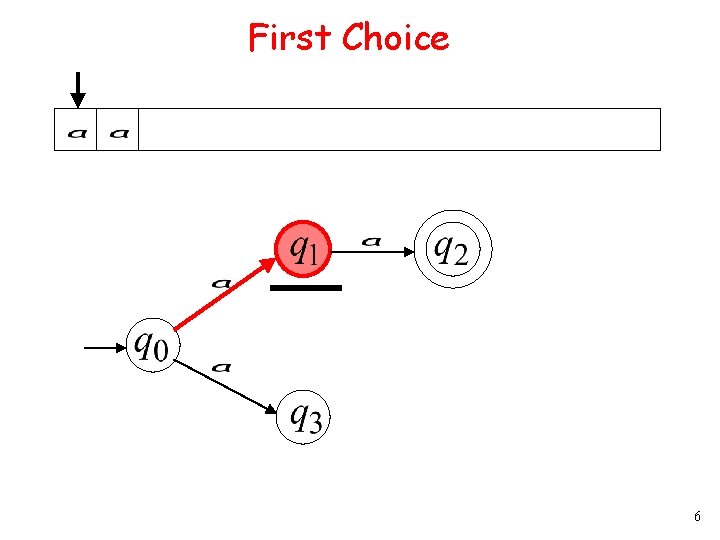
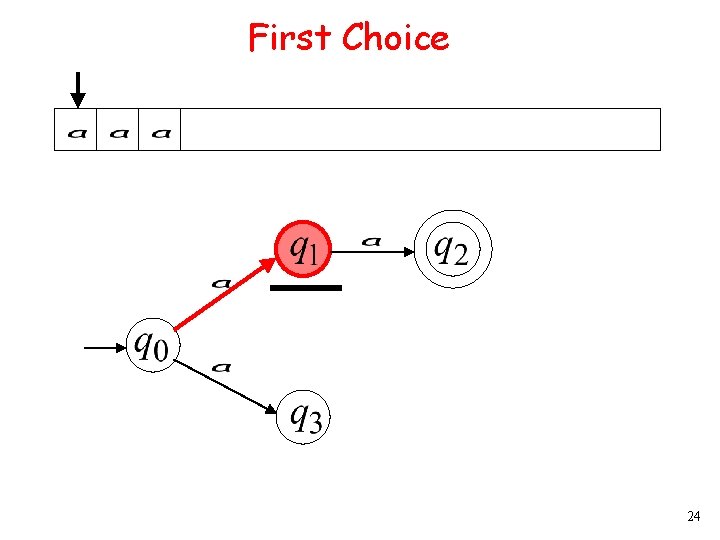
First Choice 5

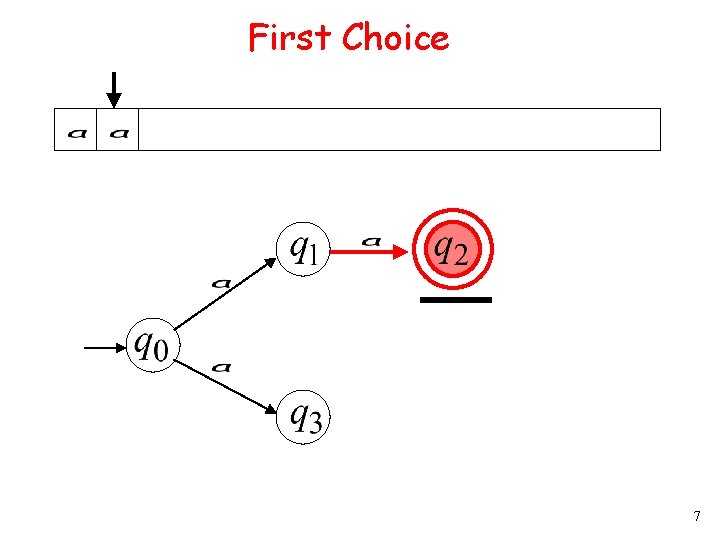
First Choice 6

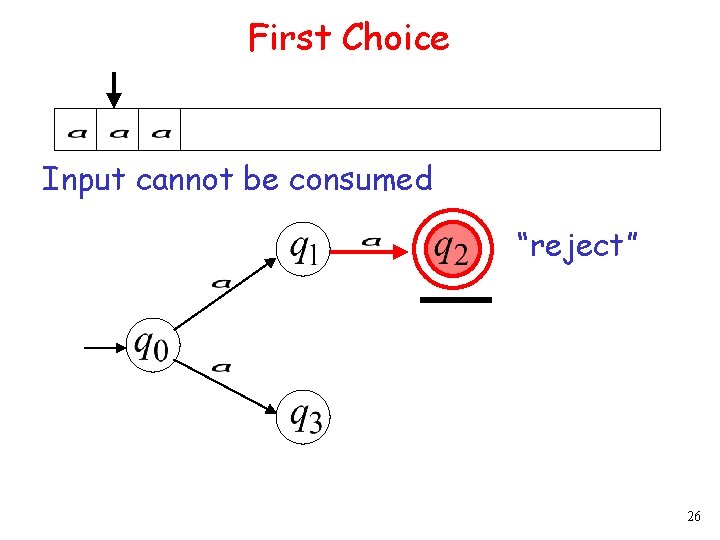
First Choice 7

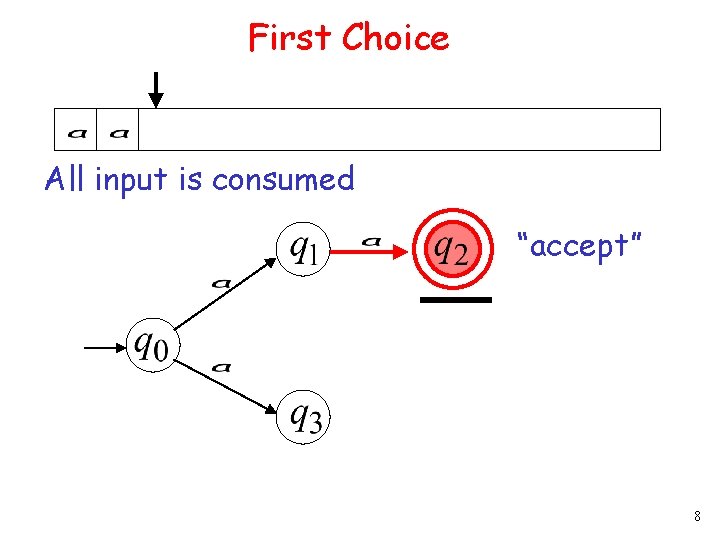
First Choice All input is consumed “accept” 8

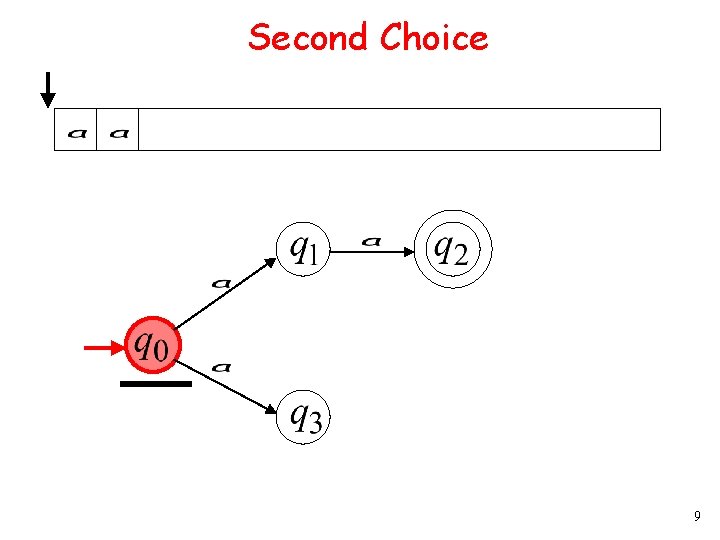
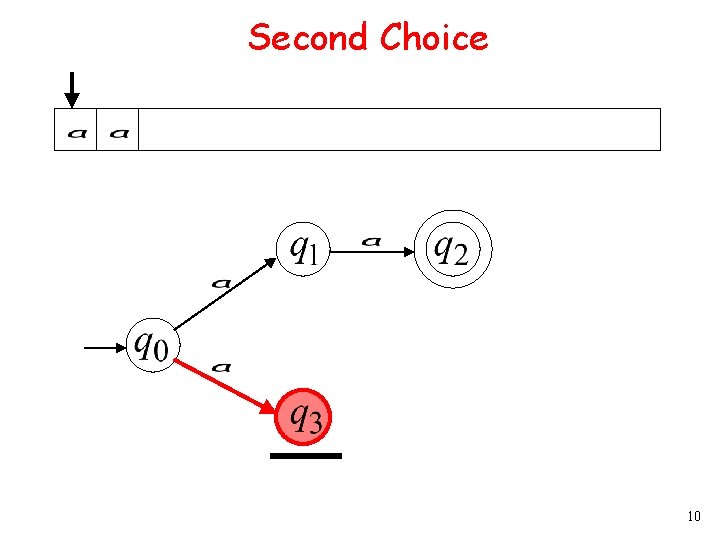
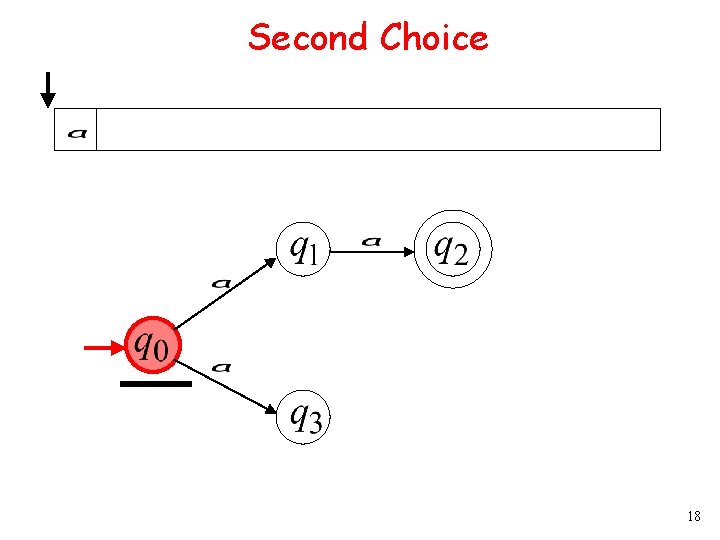
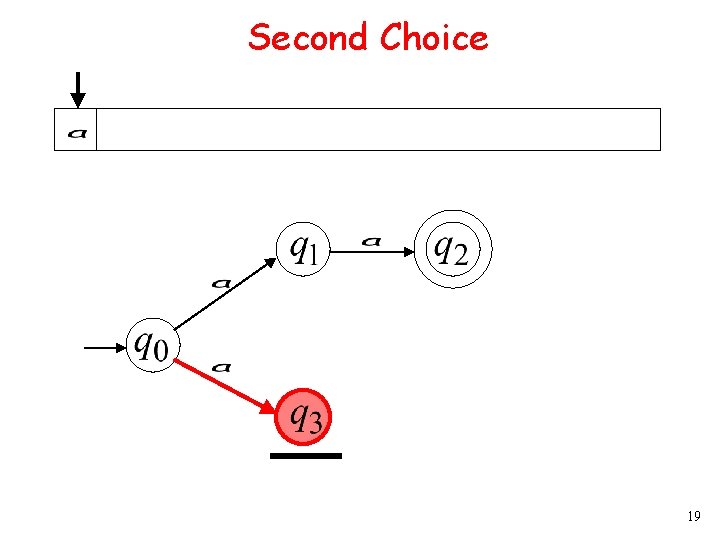
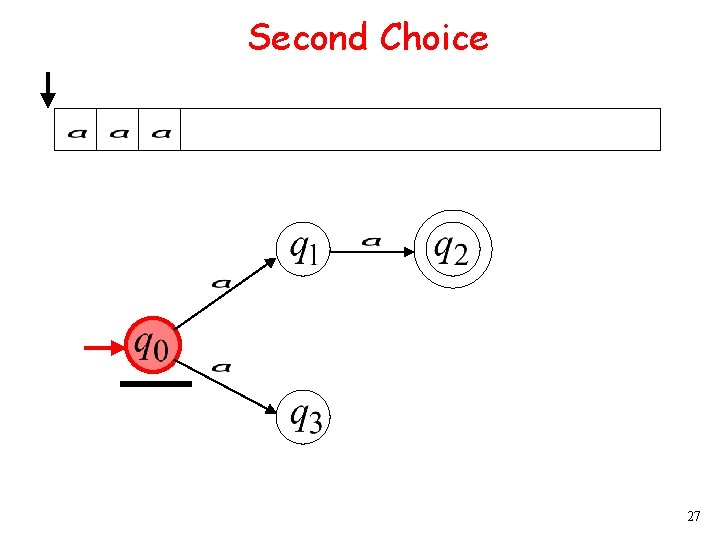
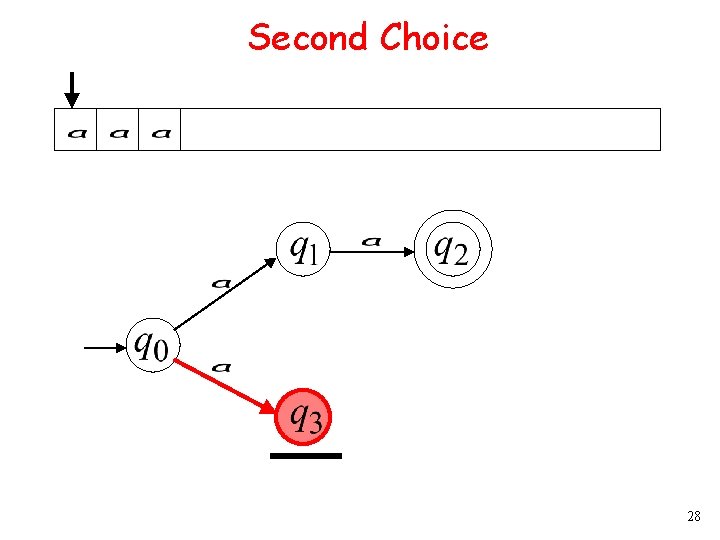
Second Choice 9

Second Choice 10

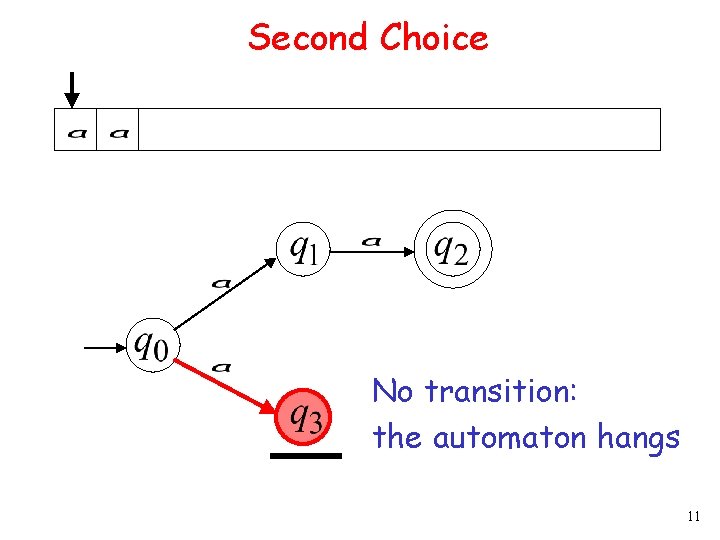
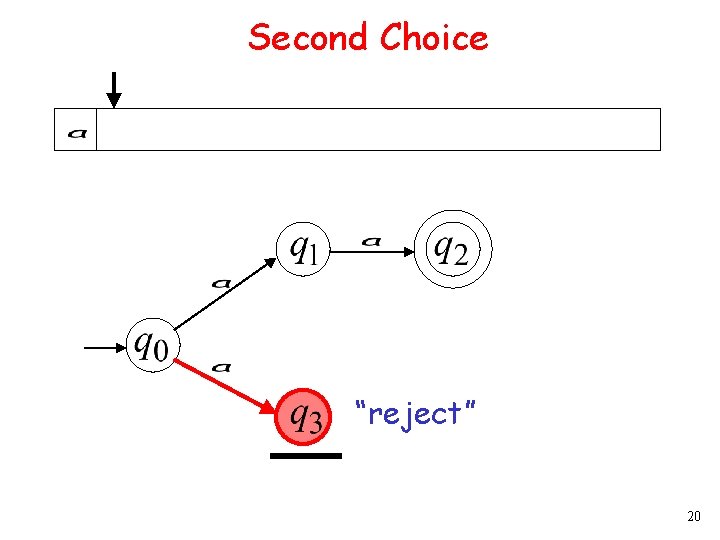
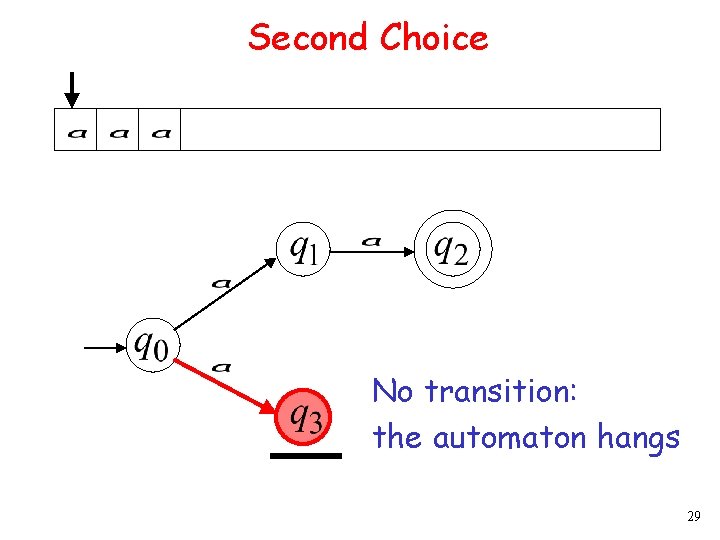
Second Choice No transition: the automaton hangs 11

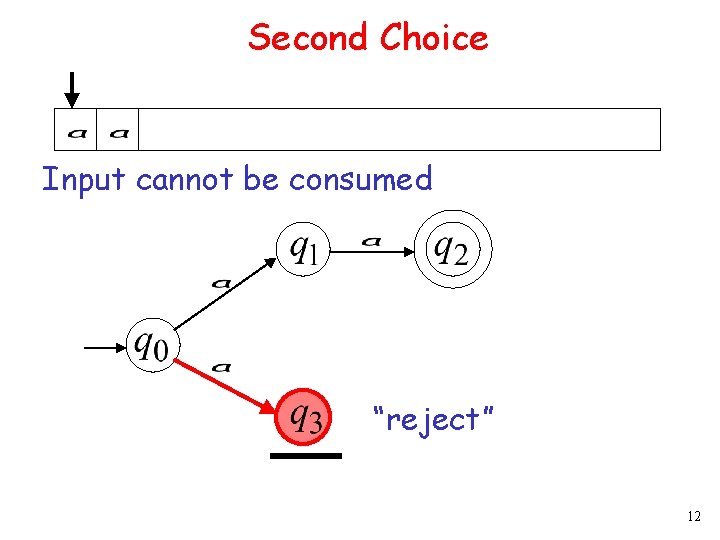
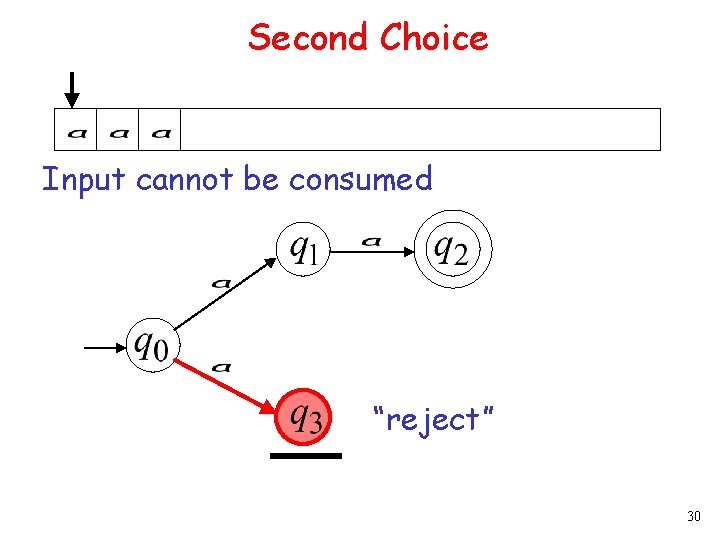
Second Choice Input cannot be consumed “reject” 12

An NFA accepts a string: when there is a computation of the NFA that accepts the string • All the input is consumed and the automaton is in a final state 13

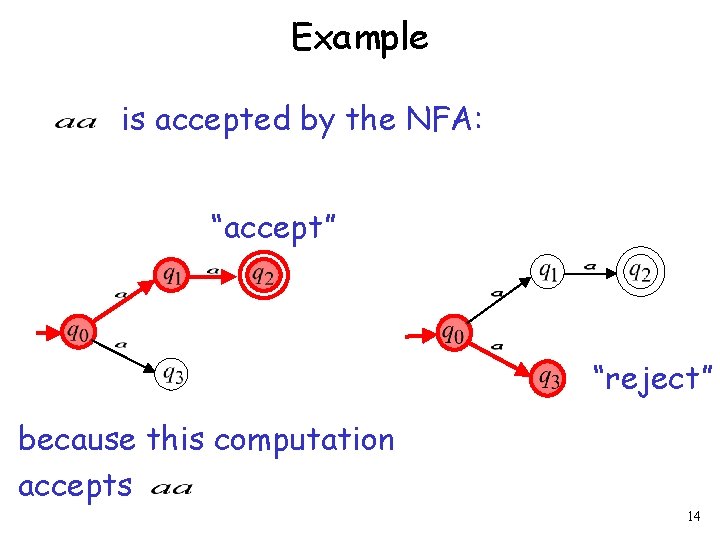
Example is accepted by the NFA: “accept” “reject” because this computation accepts 14

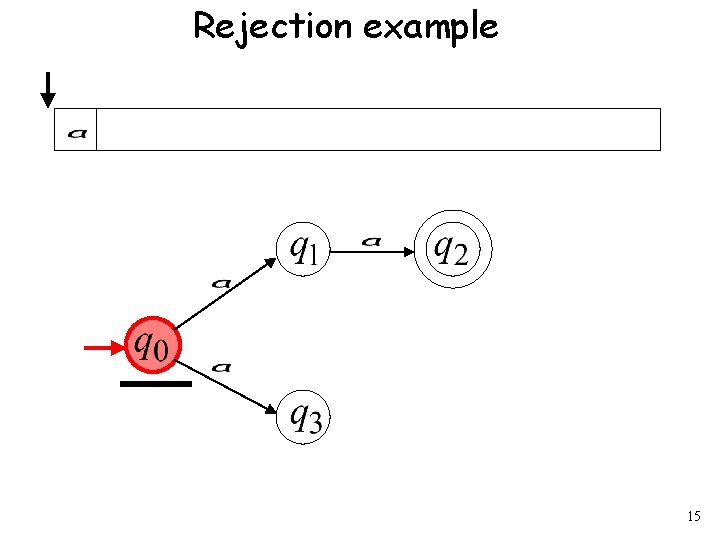
Rejection example 15

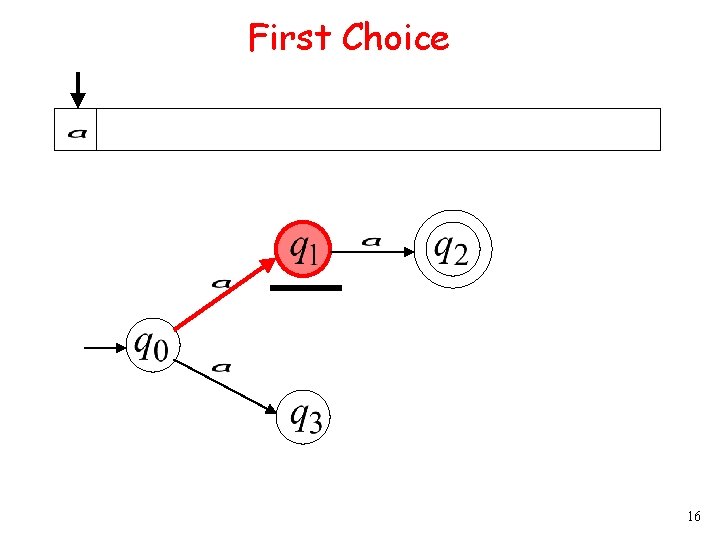
First Choice 16

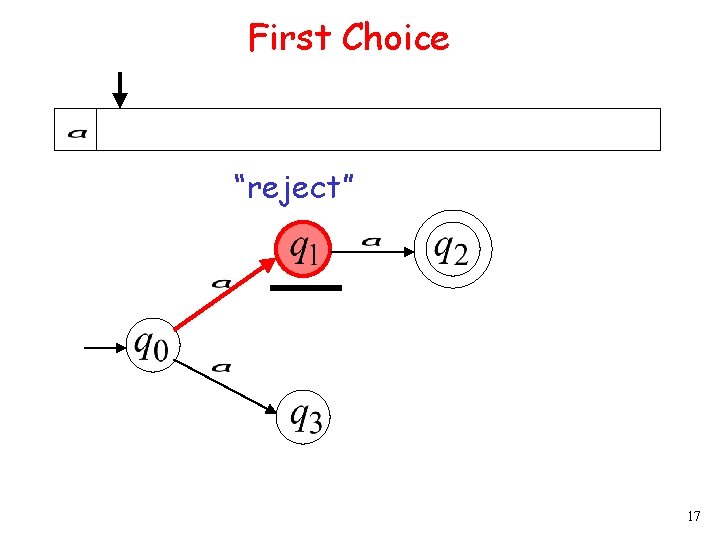
First Choice “reject” 17

Second Choice 18

Second Choice 19

Second Choice “reject” 20

An NFA rejects a string: when there is no computation of the NFA that accepts the string • All the input is consumed and the automaton is in a non final state • The input cannot be consumed 21

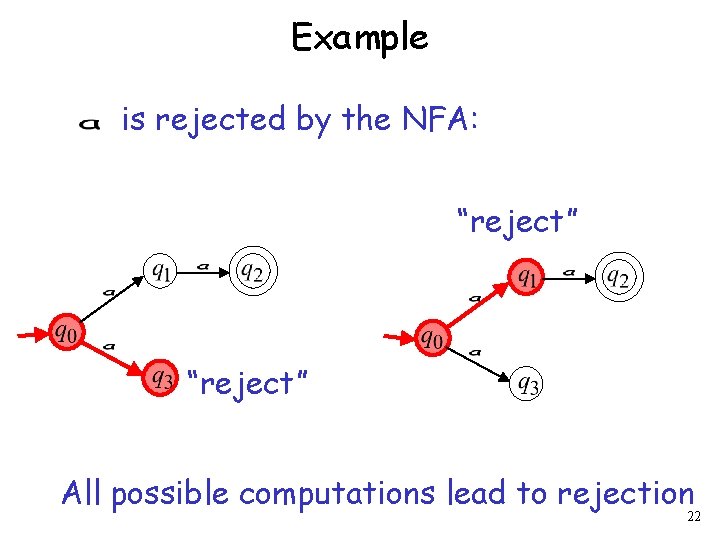
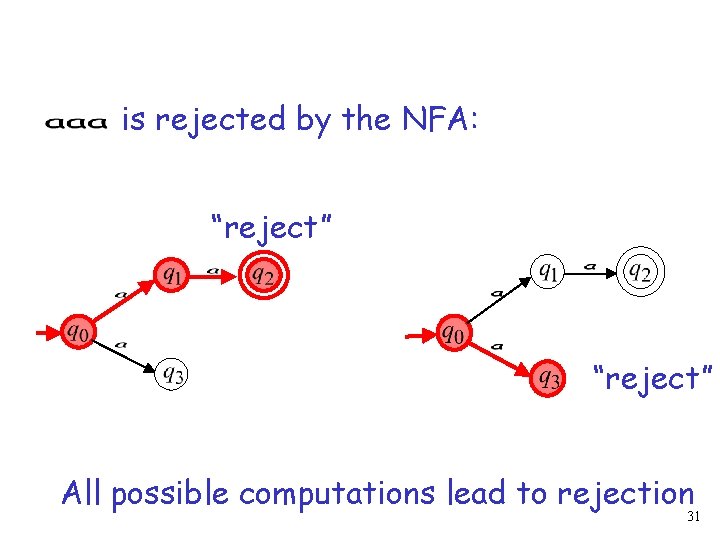
Example is rejected by the NFA: “reject” All possible computations lead to rejection 22

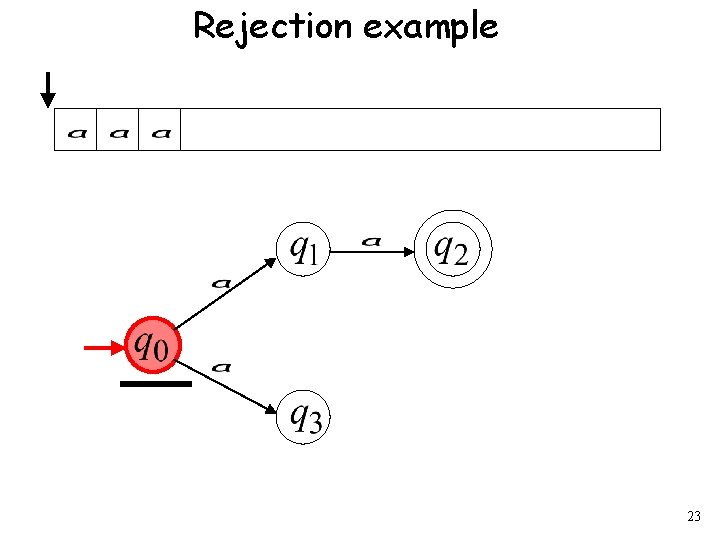
Rejection example 23

First Choice 24

First Choice No transition: the automaton hangs 25

First Choice Input cannot be consumed “reject” 26

Second Choice 27

Second Choice 28

Second Choice No transition: the automaton hangs 29

Second Choice Input cannot be consumed “reject” 30

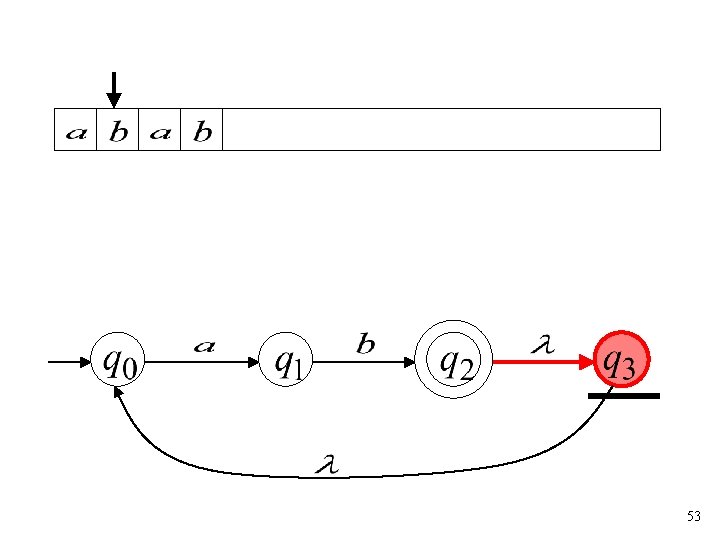
is rejected by the NFA: “reject” All possible computations lead to rejection 31

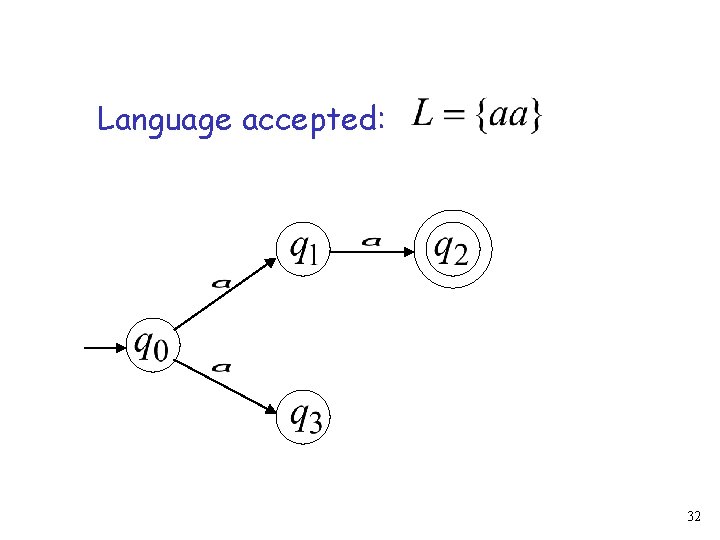
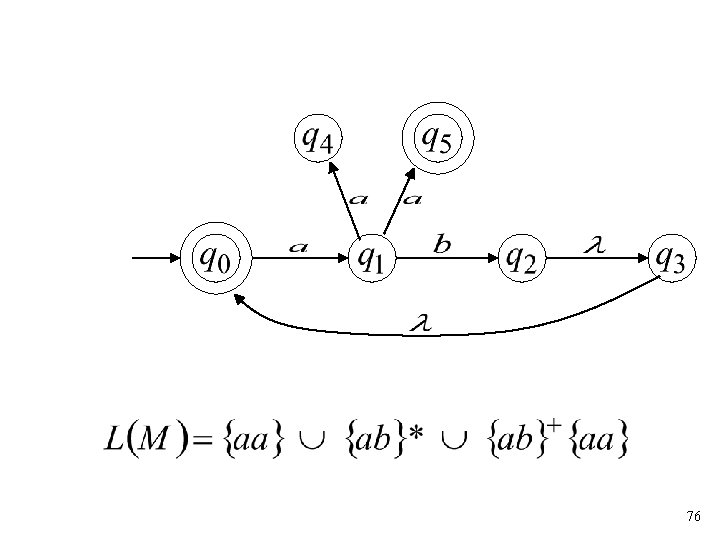
Language accepted: 32

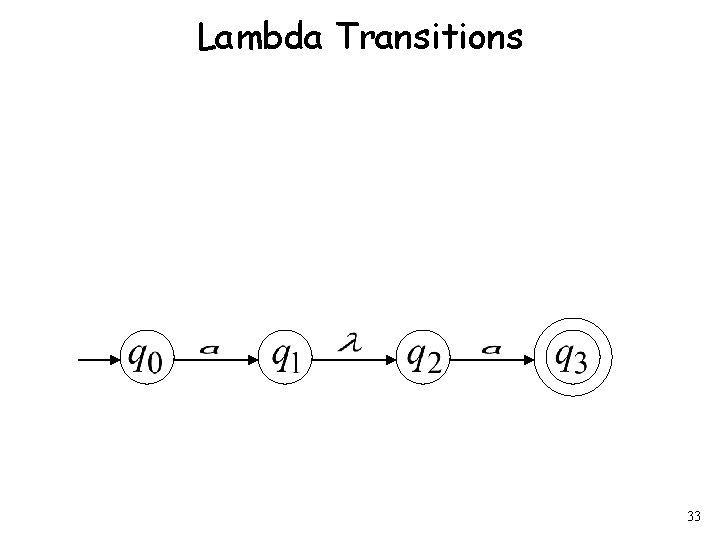
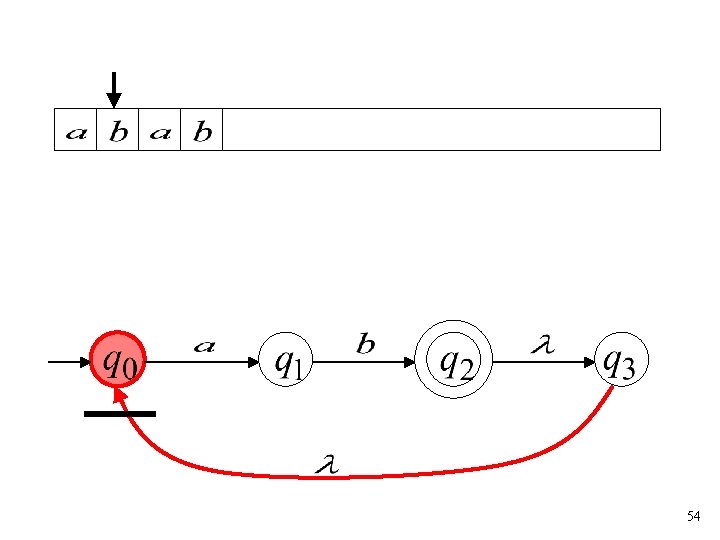
Lambda Transitions 33

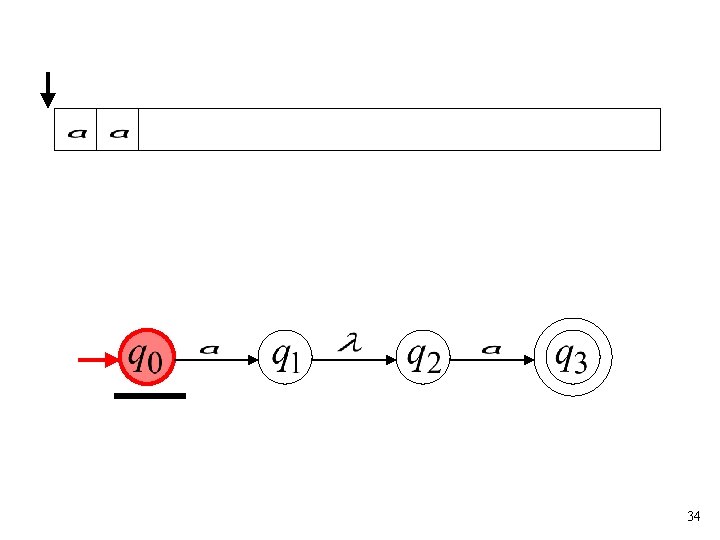
34

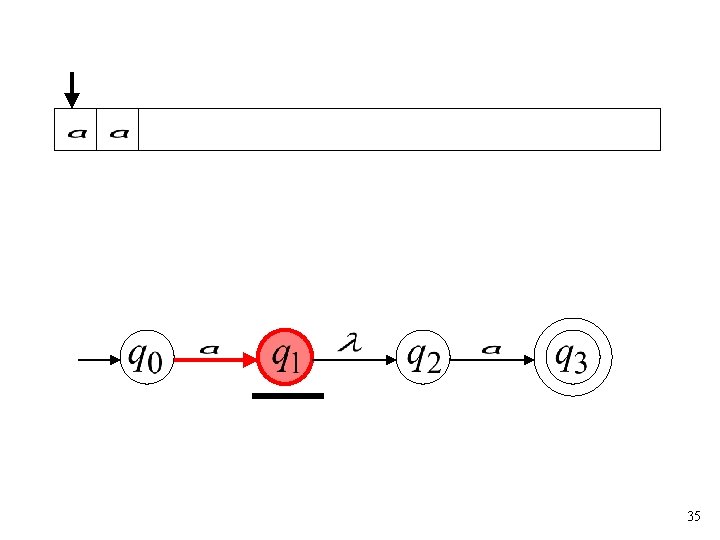
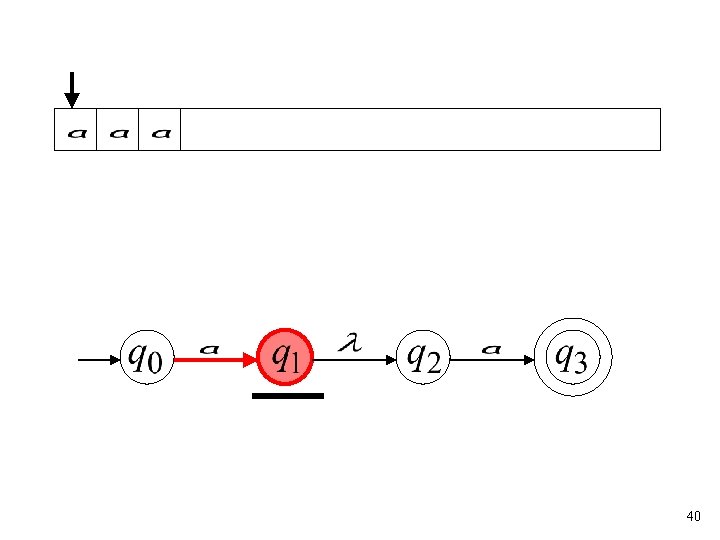
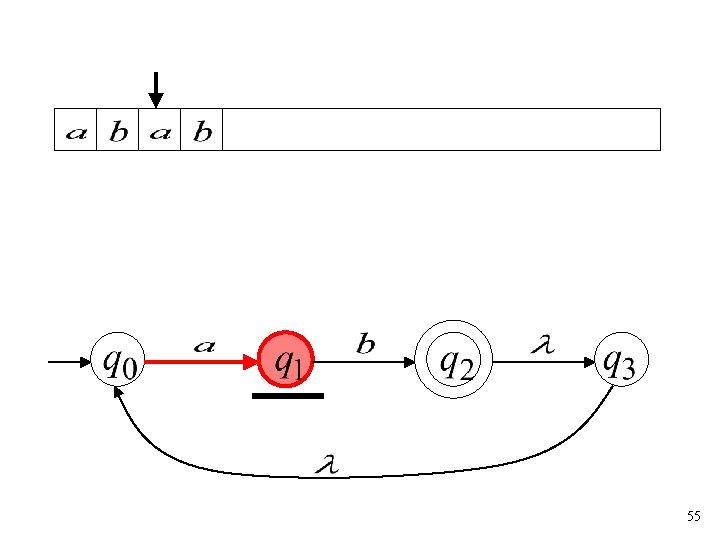
35

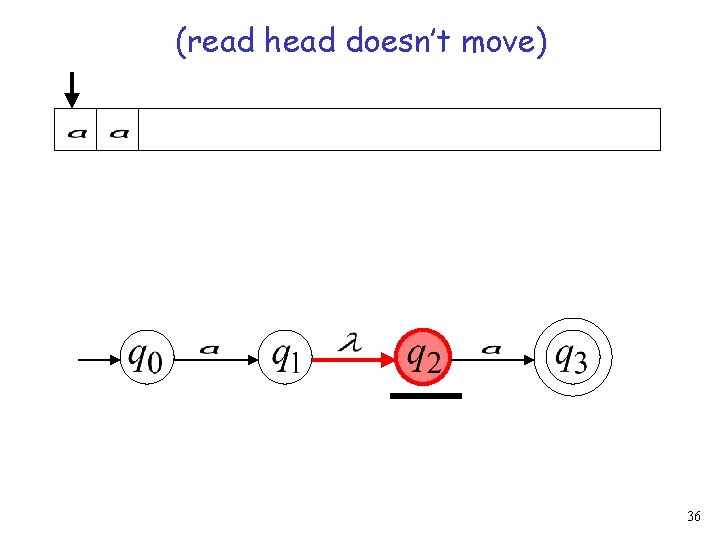
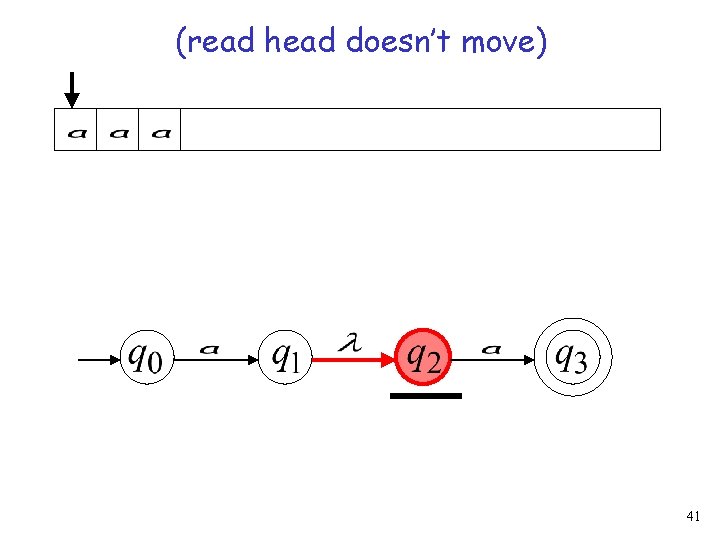
(read head doesn’t move) 36

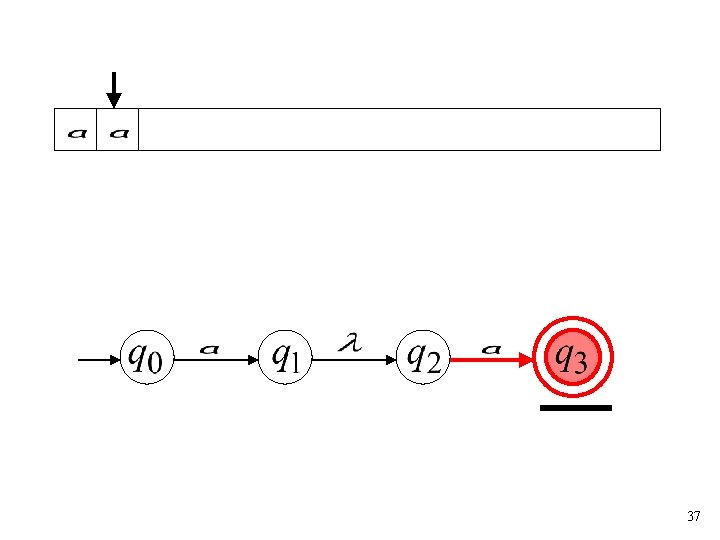
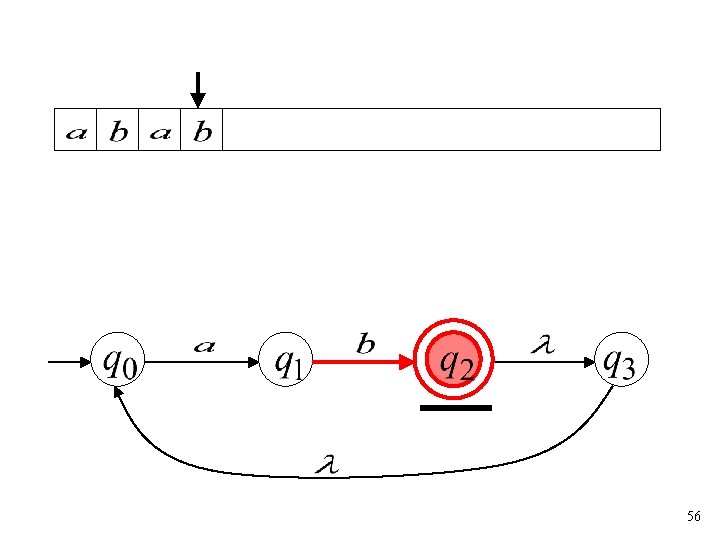
37

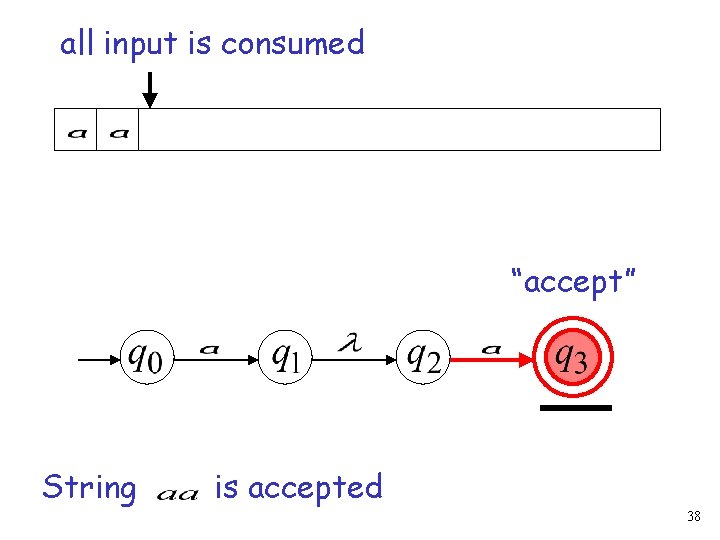
all input is consumed “accept” String is accepted 38

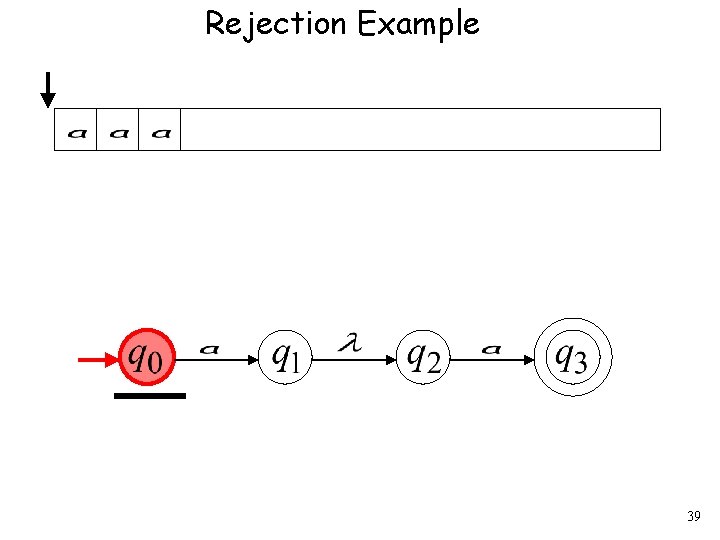
Rejection Example 39

40

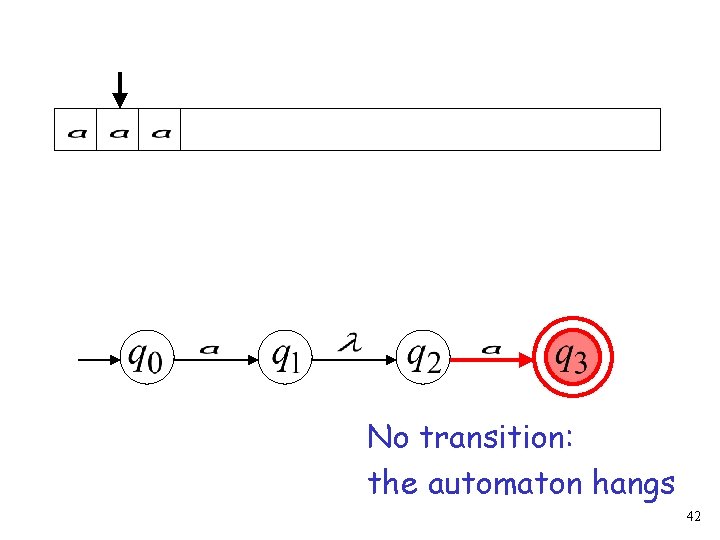
(read head doesn’t move) 41

No transition: the automaton hangs 42

Input cannot be consumed “reject” String is rejected 43
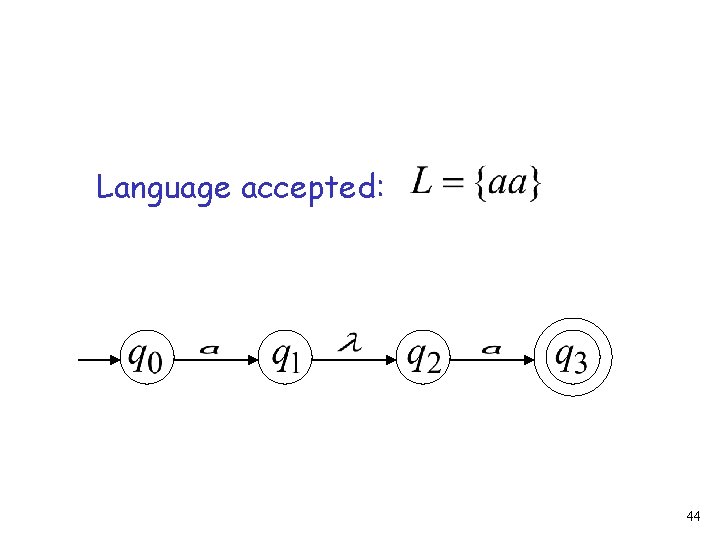
Language accepted: 44

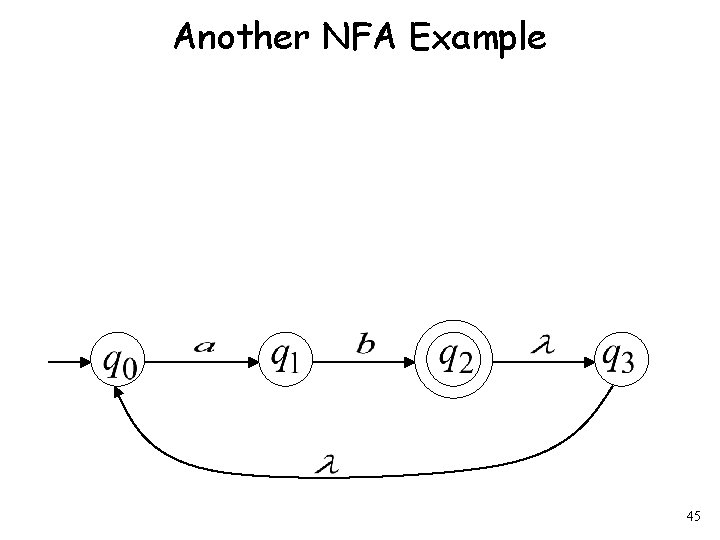
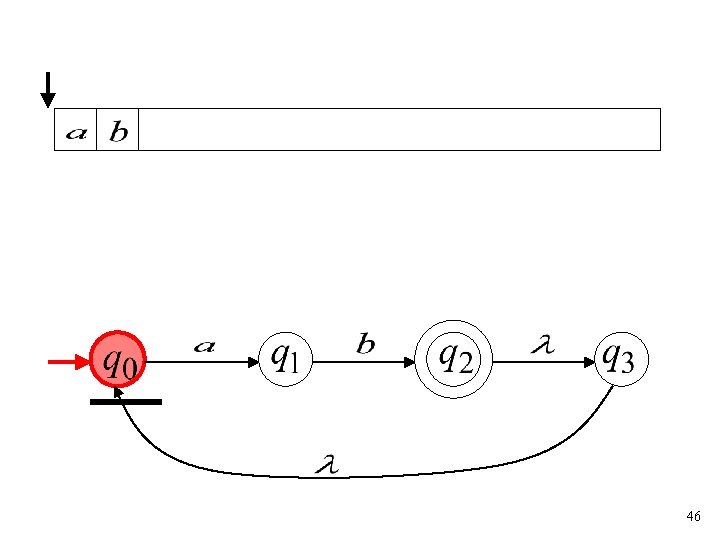
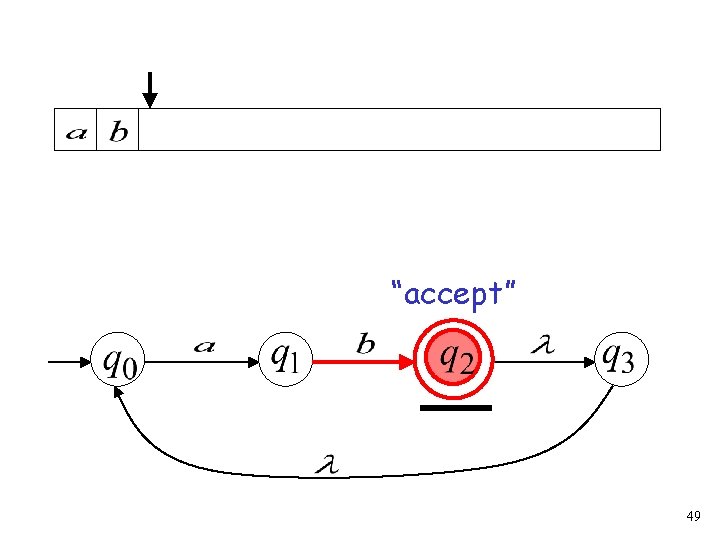
Another NFA Example 45

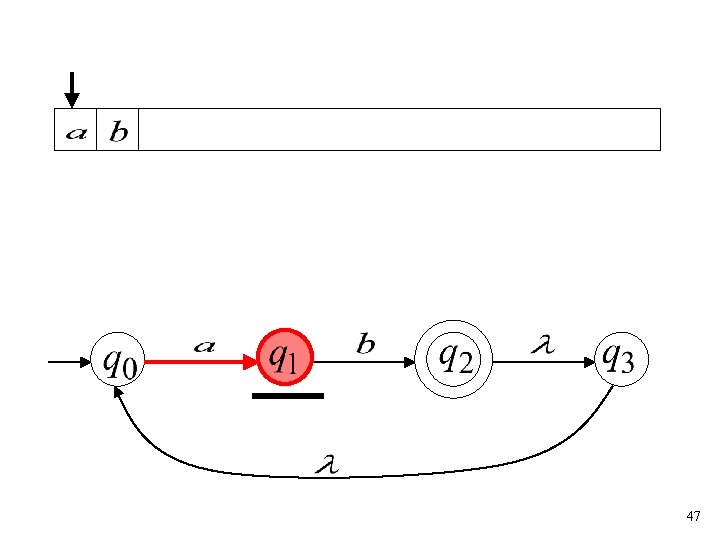
46

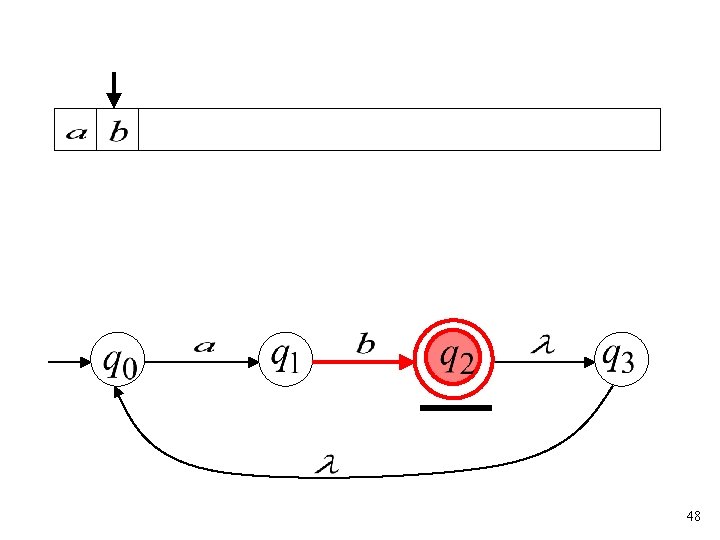
47

48

“accept” 49

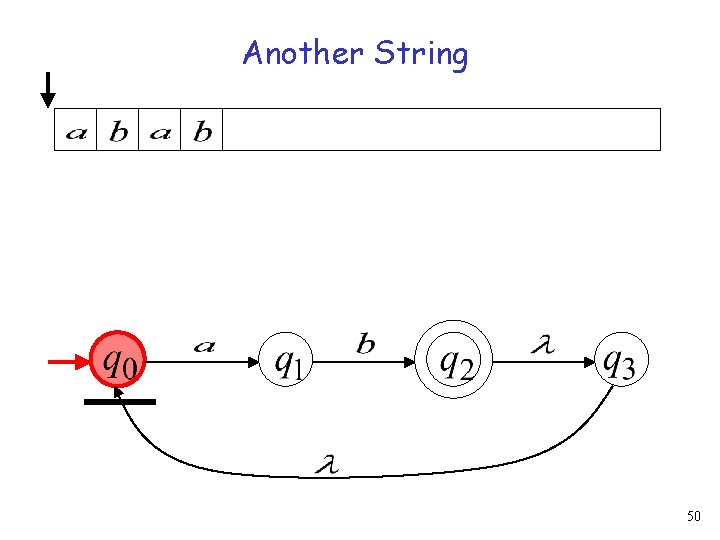
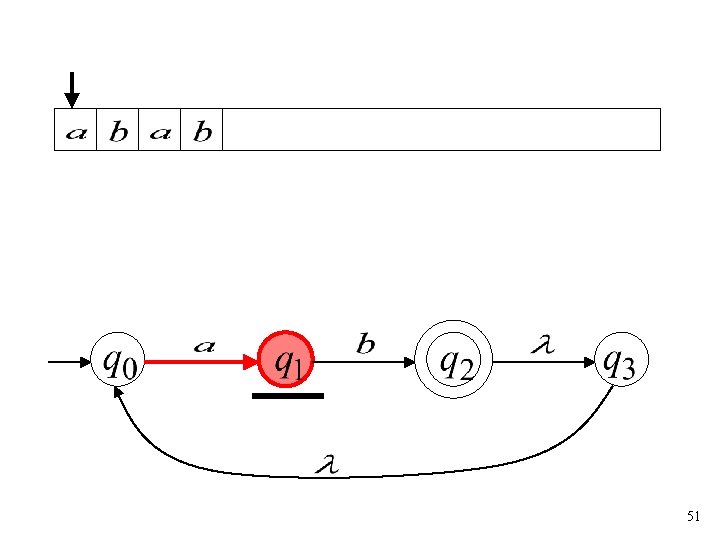
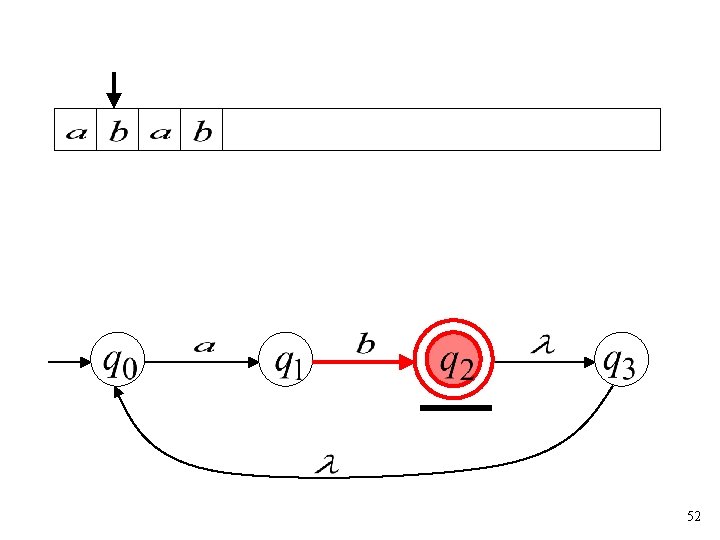
Another String 50

51

52

53

54

55

56

“accept” 57

Language accepted 58

Another NFA Example 59

Language accepted 60

Remarks: • The symbol never appears on the input tape • Extreme automata: 61

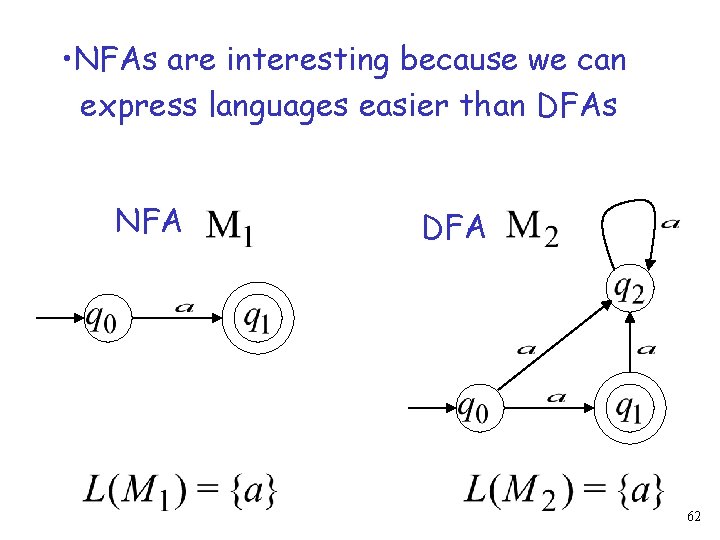
• NFAs are interesting because we can express languages easier than DFAs NFA DFA 62

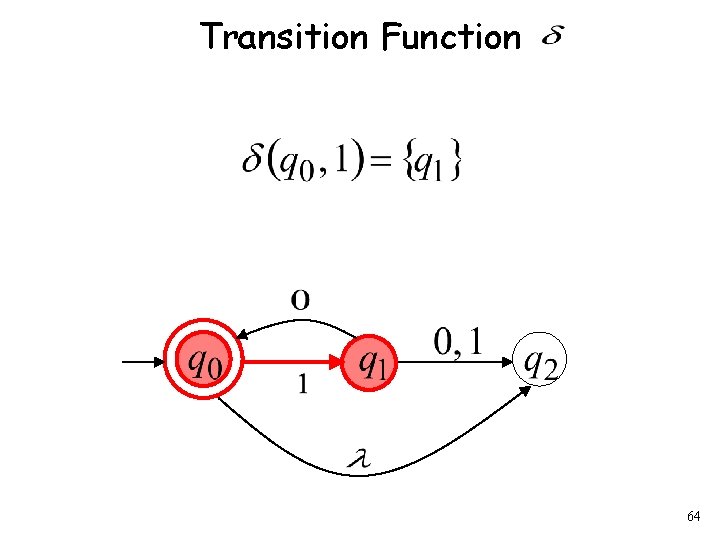
Formal Definition of NFAs Set of states, i. e. Input aplhabet, i. e. Transition function Initial state Final states 63

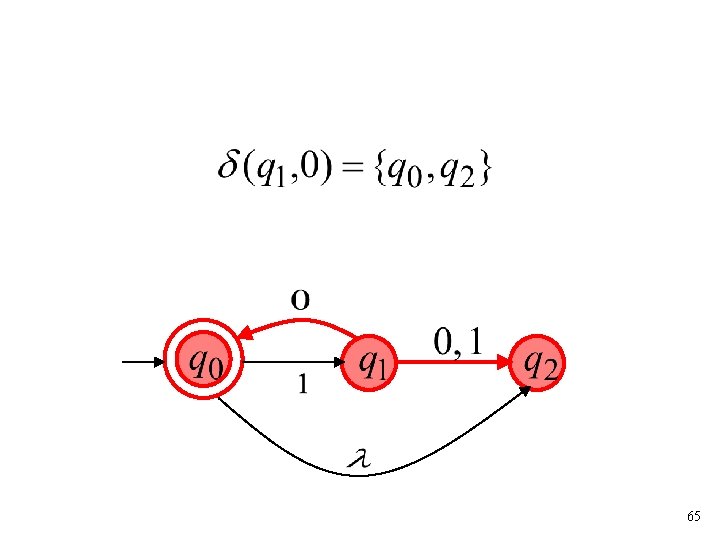
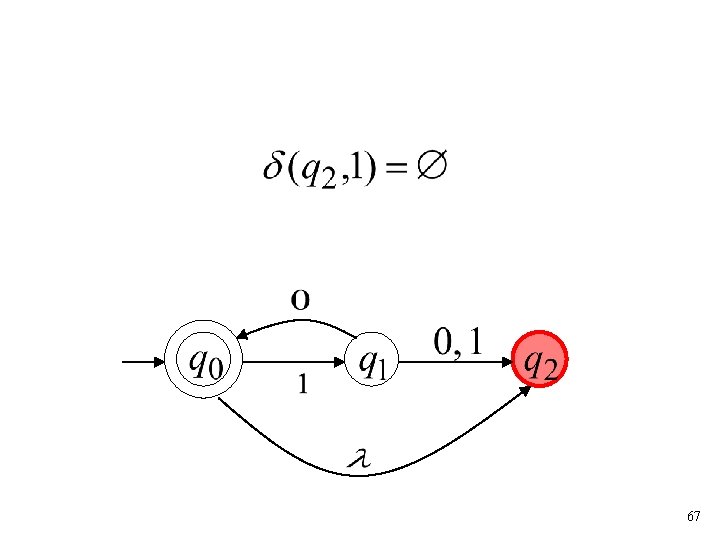
Transition Function 64

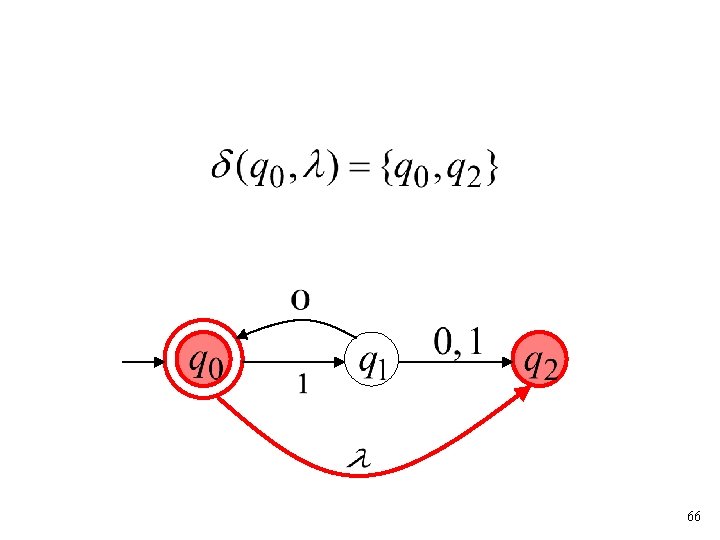
65

66

67

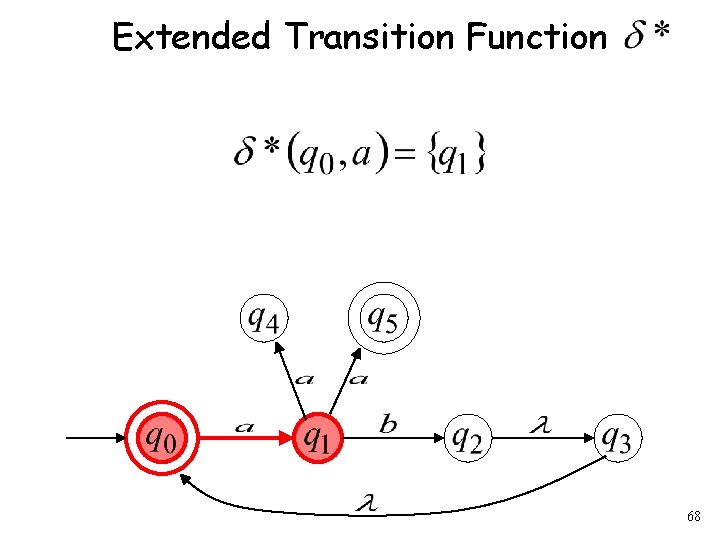
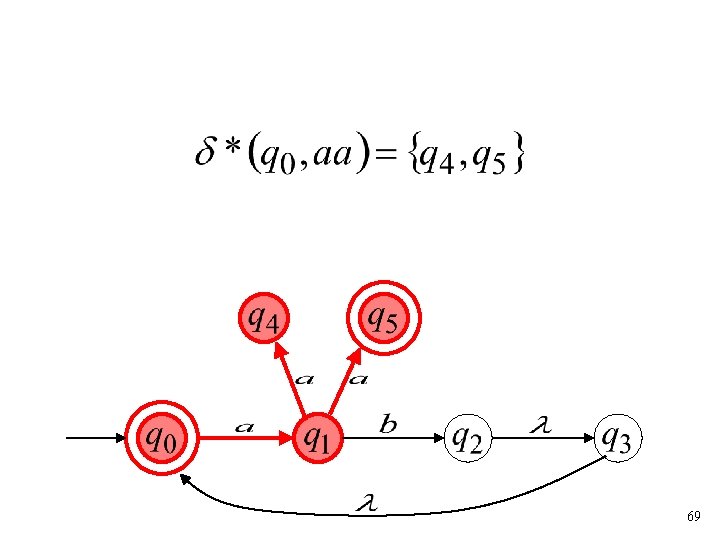
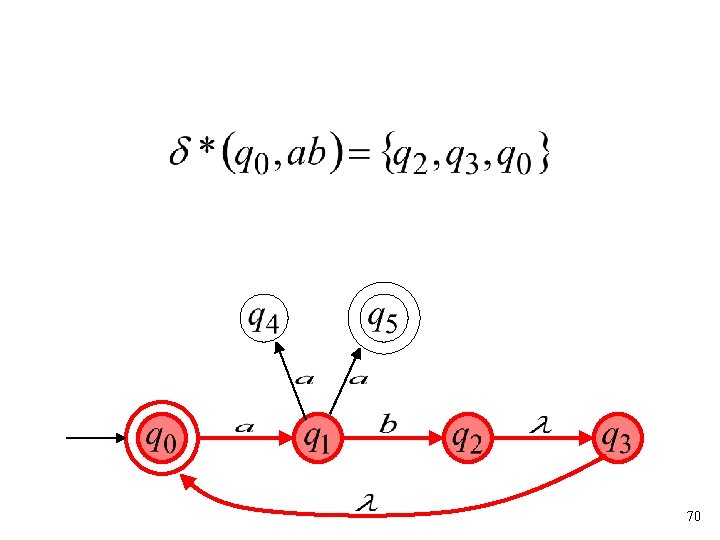
Extended Transition Function 68

69

70

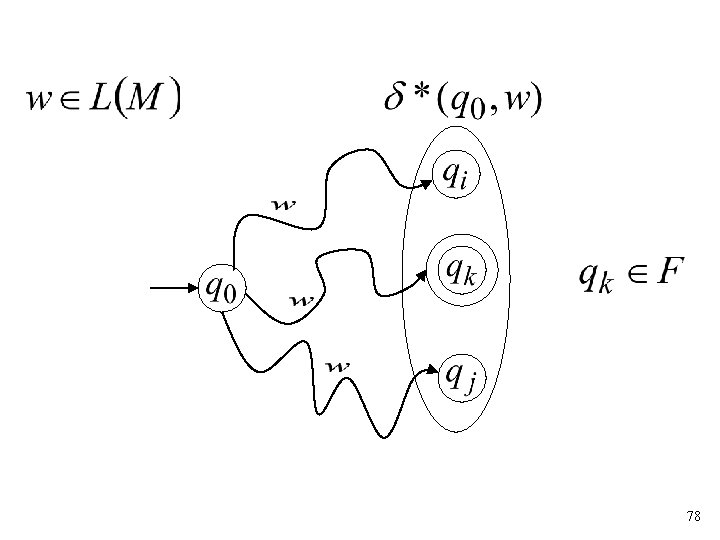
Formally It holds if and only if there is a walk from with label to 71

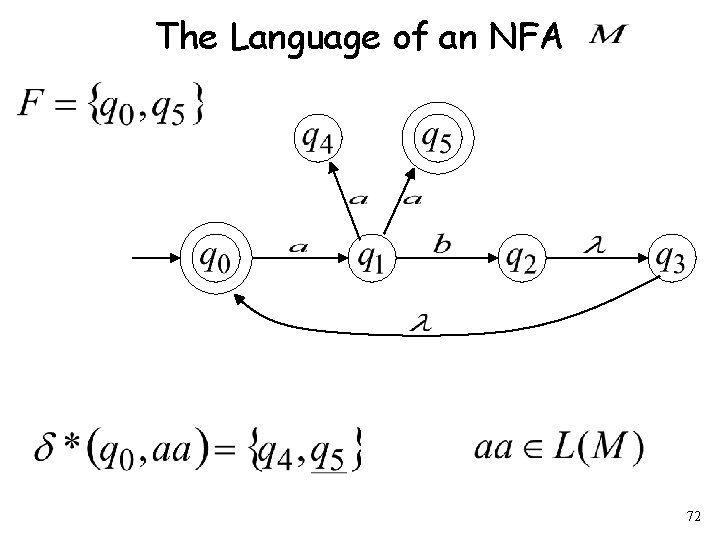
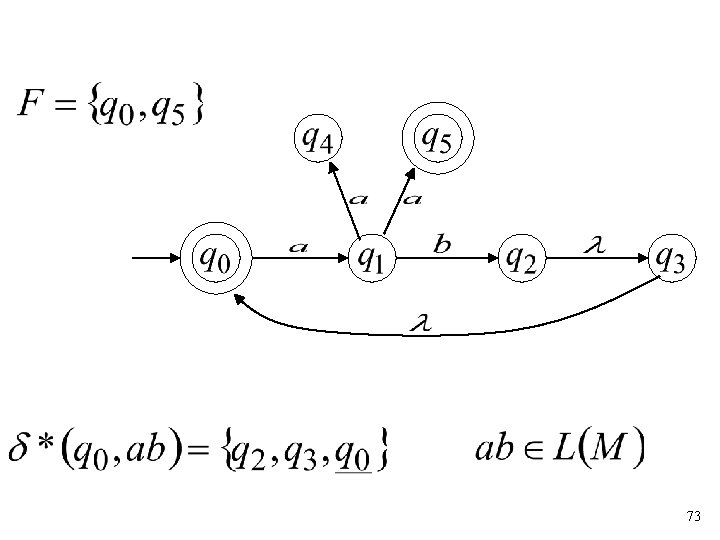
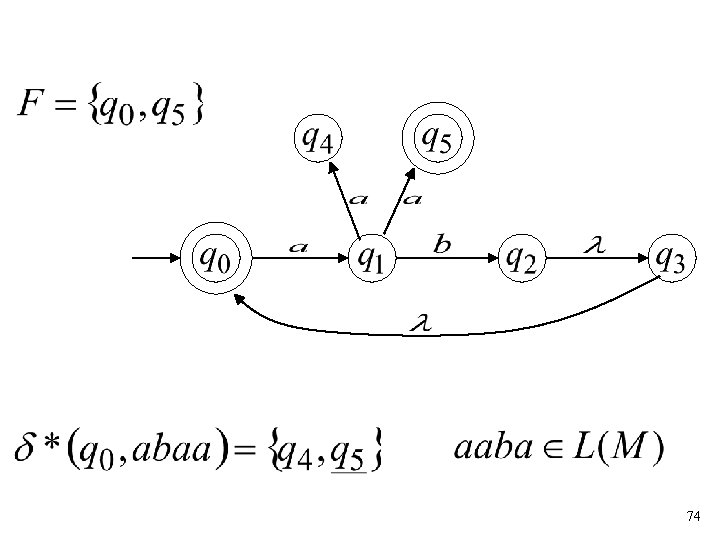
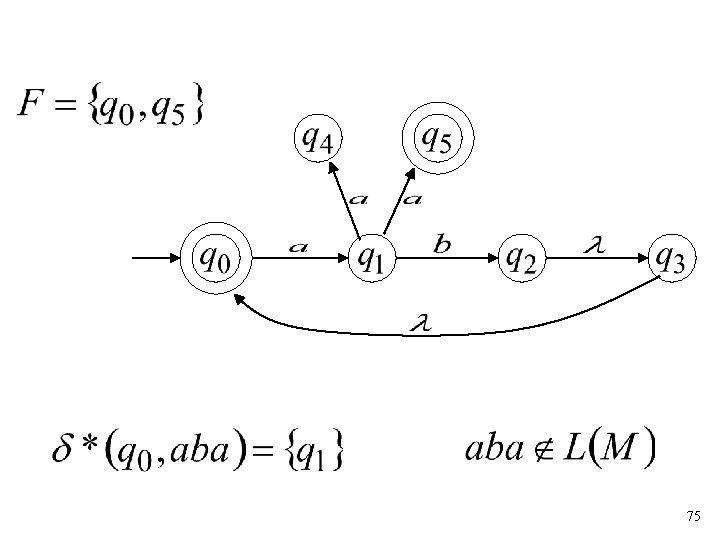
The Language of an NFA 72

73

74

75

76

Formally The language accepted by NFA is: where and there is some (final state) 77

78

Equivalence of NFAs and DFAs 79

Equivalence of Machines For DFAs or NFAs: Machine is equivalent to machine if 80

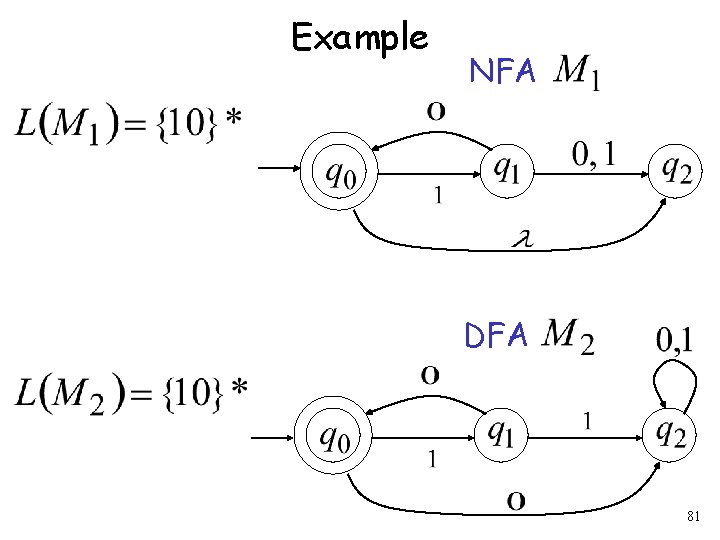
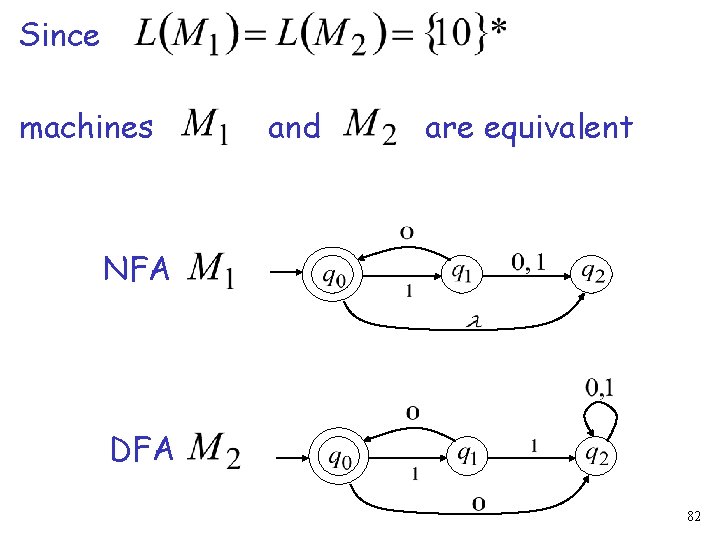
Example NFA DFA 81

Since machines and are equivalent NFA DFA 82

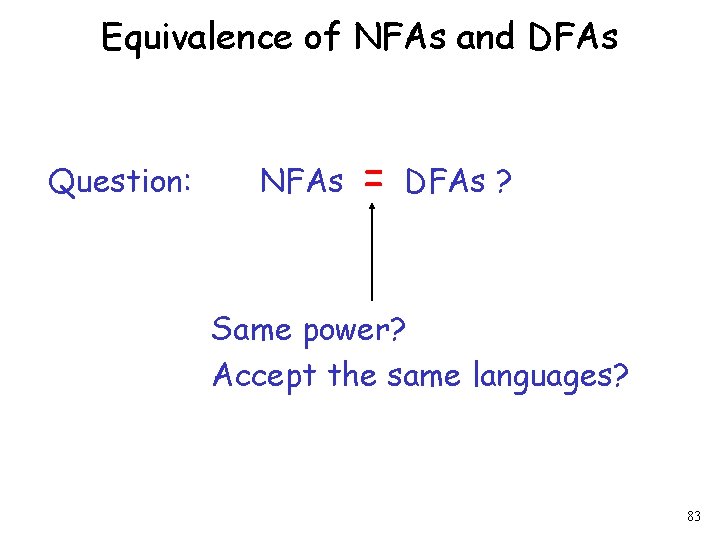
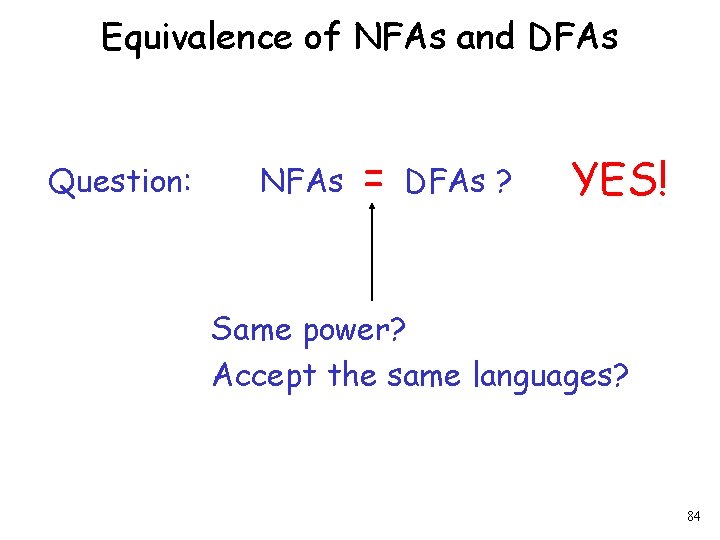
Equivalence of NFAs and DFAs Question: NFAs = DFAs ? Same power? Accept the same languages? 83

Equivalence of NFAs and DFAs Question: NFAs = DFAs ? YES! Same power? Accept the same languages? 84

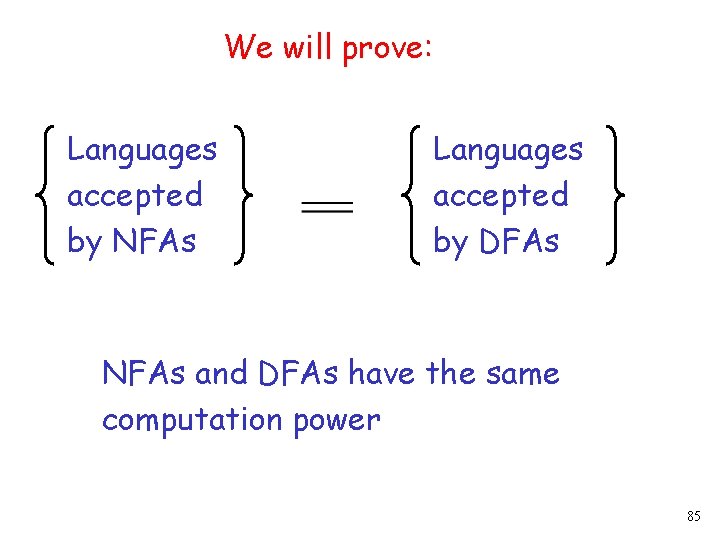
We will prove: Languages accepted by NFAs Languages accepted by DFAs NFAs and DFAs have the same computation power 85

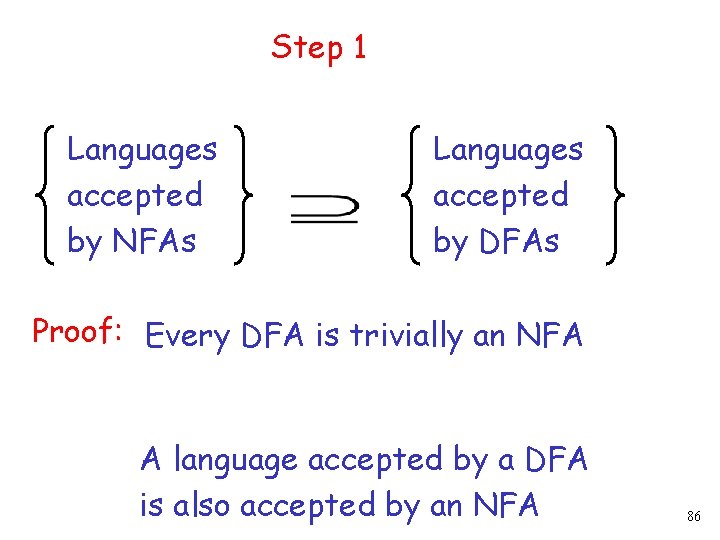
Step 1 Languages accepted by NFAs Languages accepted by DFAs Proof: Every DFA is trivially an NFA A language accepted by a DFA is also accepted by an NFA 86

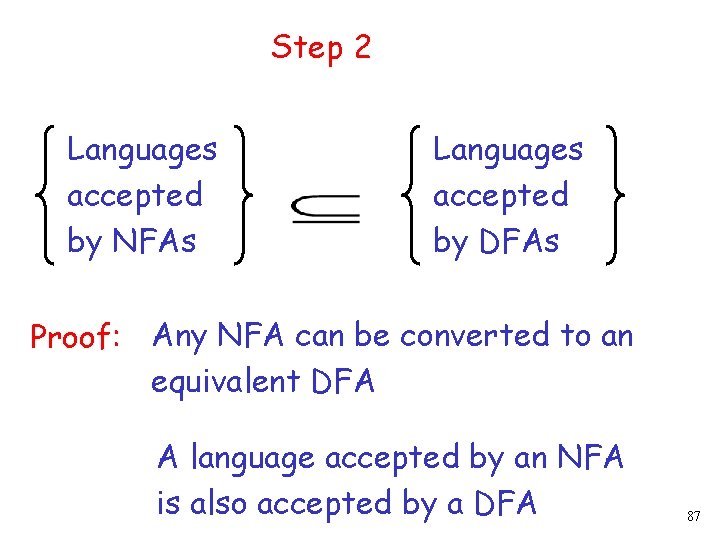
Step 2 Languages accepted by NFAs Languages accepted by DFAs Proof: Any NFA can be converted to an equivalent DFA A language accepted by an NFA is also accepted by a DFA 87

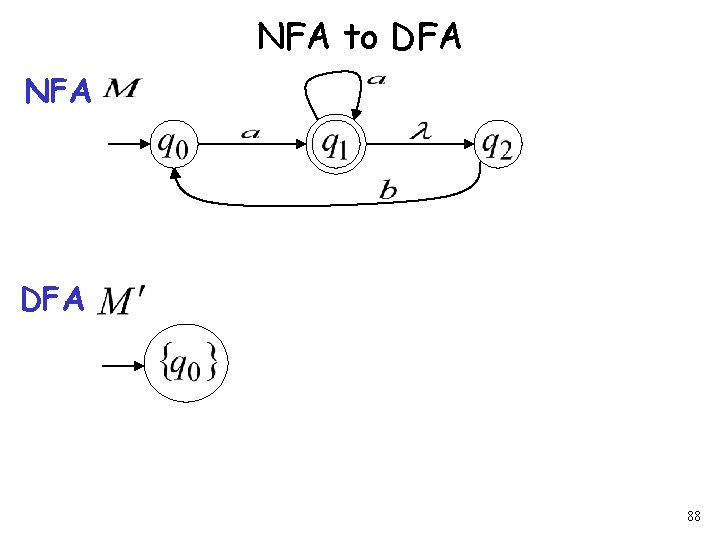
NFA to DFA NFA DFA 88

NFA to DFA NFA DFA 89

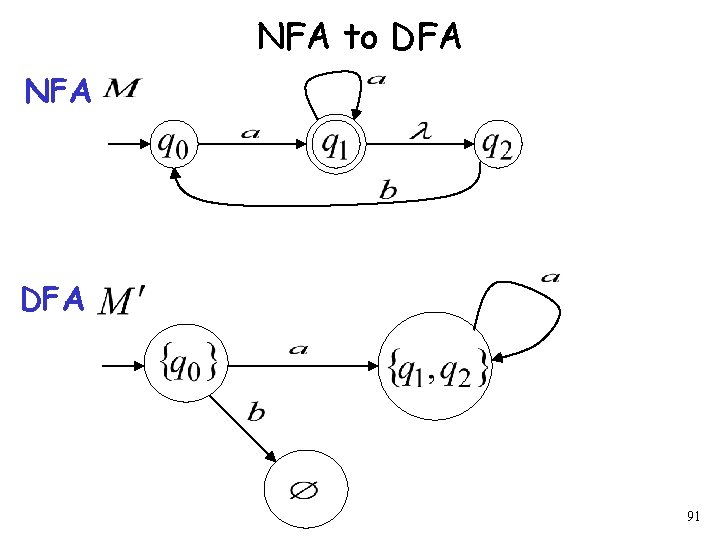
NFA to DFA NFA DFA 90

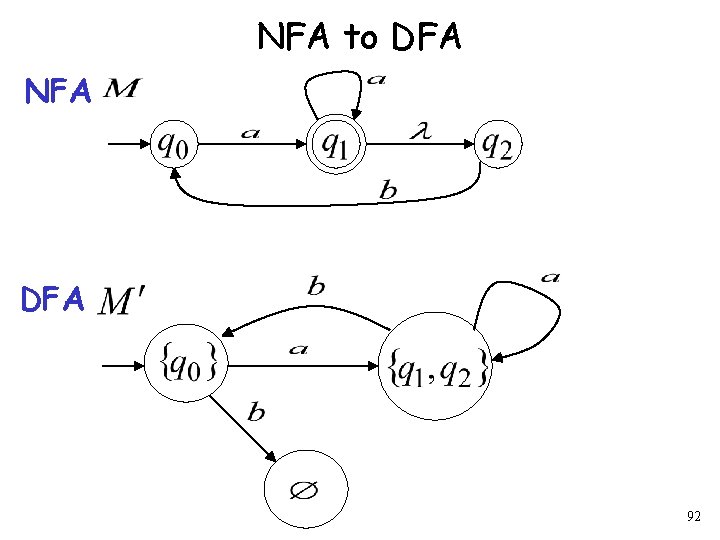
NFA to DFA NFA DFA 91

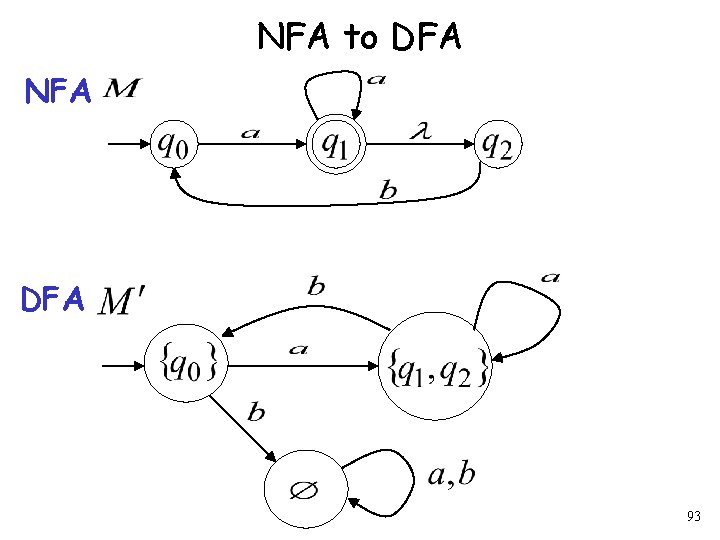
NFA to DFA NFA DFA 92

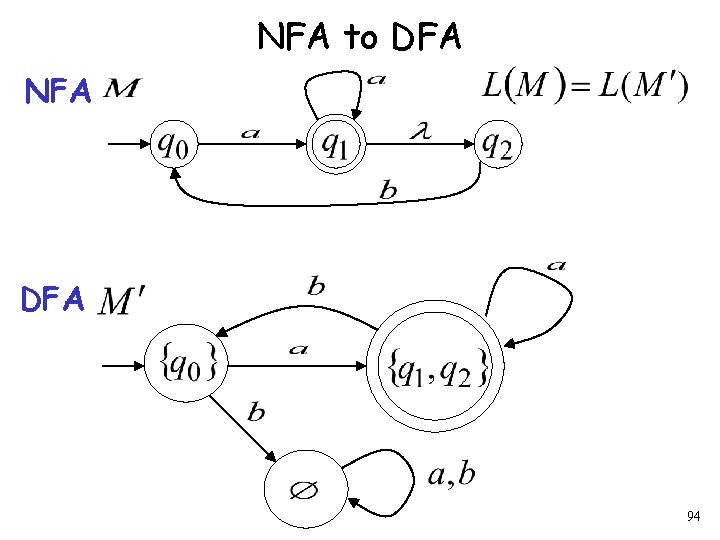
NFA to DFA NFA DFA 93

NFA to DFA NFA DFA 94

NFA to DFA: Remarks We are given an NFA We want to convert it to an equivalent DFA With 95

If the NFA has states the DFA has states in the powerset 96

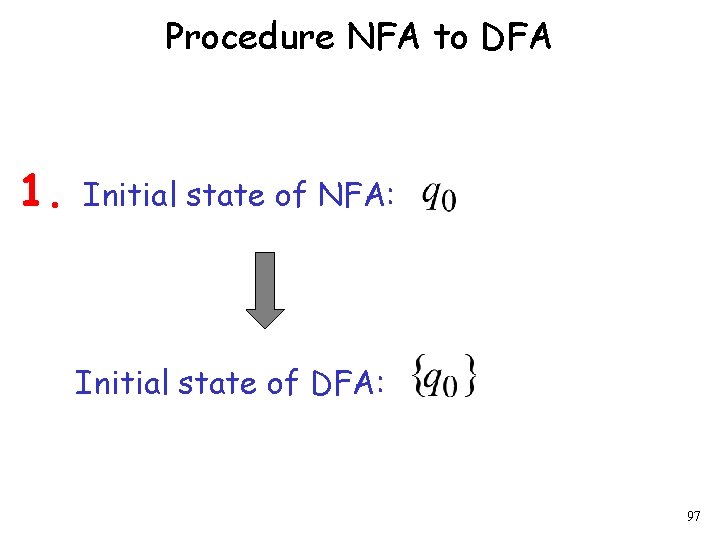
Procedure NFA to DFA 1. Initial state of NFA: Initial state of DFA: 97

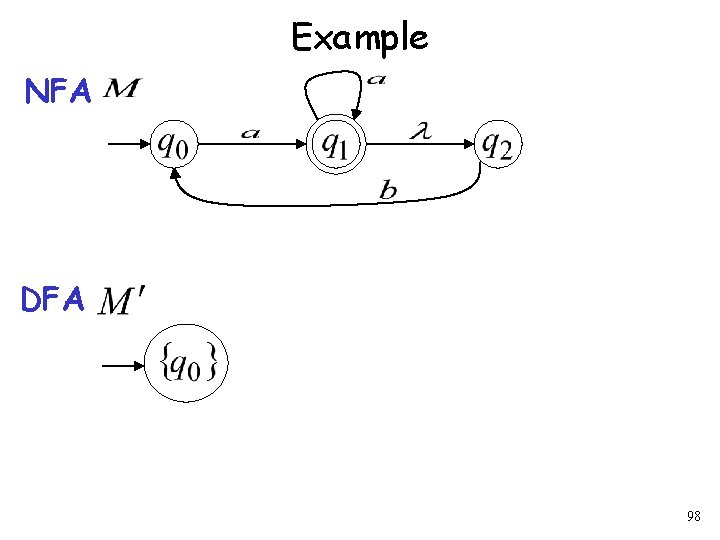
Example NFA DFA 98

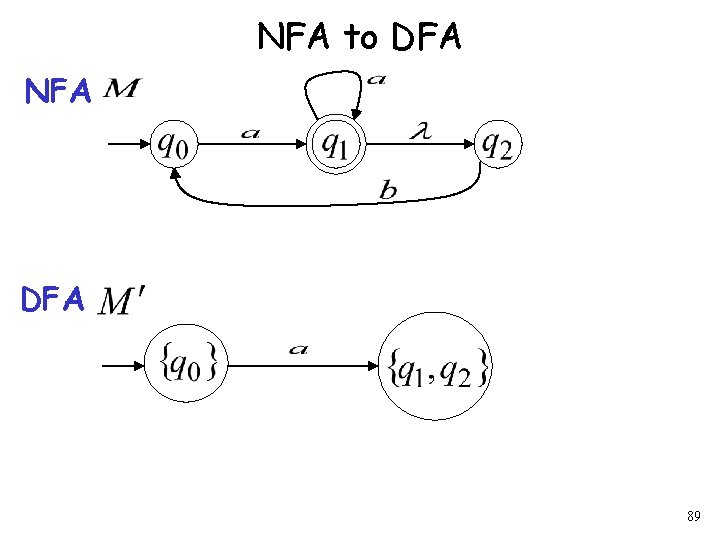
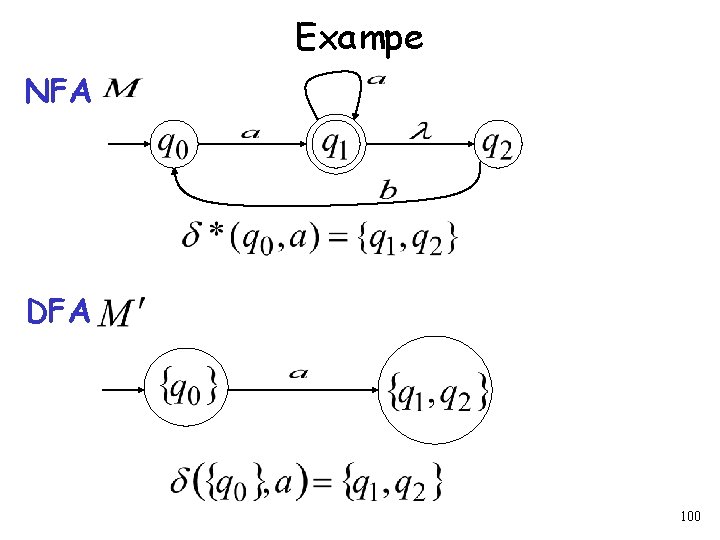
Procedure NFA to DFA 2. For every DFA’s state Compute in the NFA Add transition to DFA 99

Exampe NFA DFA 100

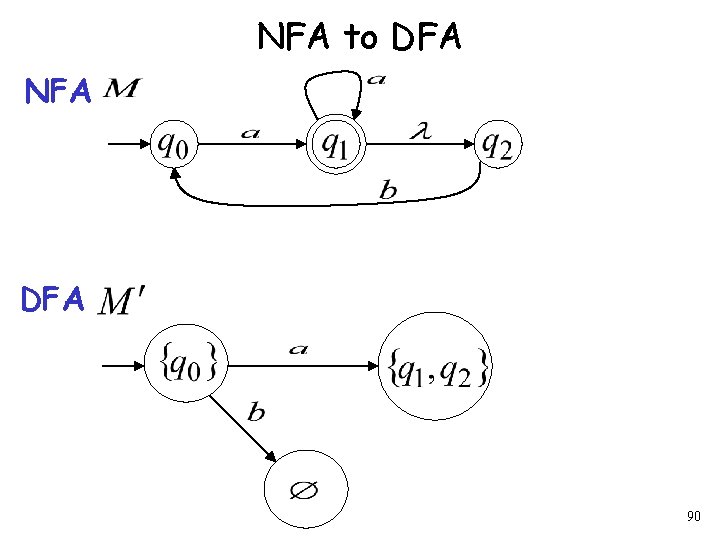
Procedure NFA to DFA Repeat Step 2 for all letters in alphabet, until no more transitions can be added. 101

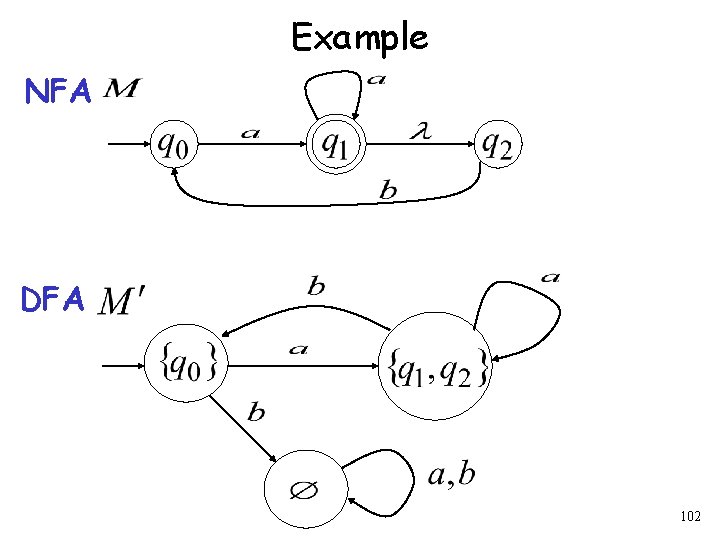
Example NFA DFA 102

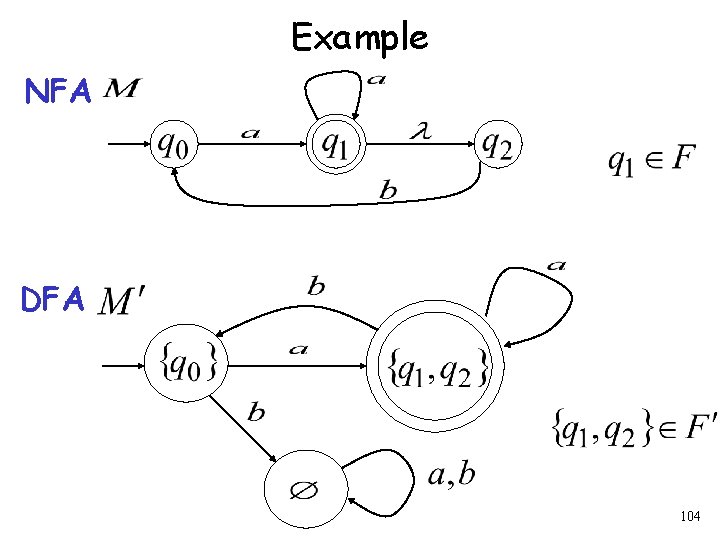
Procedure NFA to DFA 3. For any DFA state If some is a final state in the NFA Then, is a final state in the DFA 103

Example NFA DFA 104

Theorem Take NFA Apply procedure to obtain DFA Then and are equivalent : 105

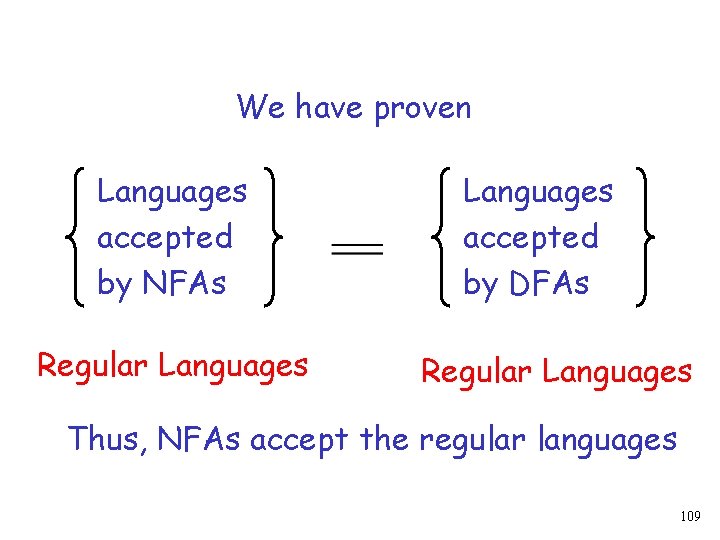
Finally We have proven Languages accepted by NFAs Languages accepted by DFAs 106

We have proven Languages accepted by NFAs Languages accepted by DFAs Regular Languages 107

We have proven Languages accepted by NFAs Regular Languages accepted by DFAs Regular Languages 108

We have proven Languages accepted by NFAs Regular Languages accepted by DFAs Regular Languages Thus, NFAs accept the regular languages 109