Nodal Analysis Discussion D 2 3 Chapter 2





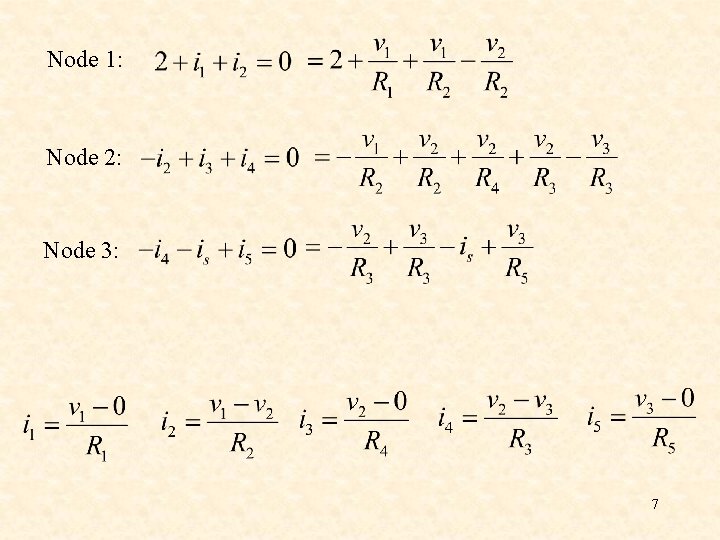
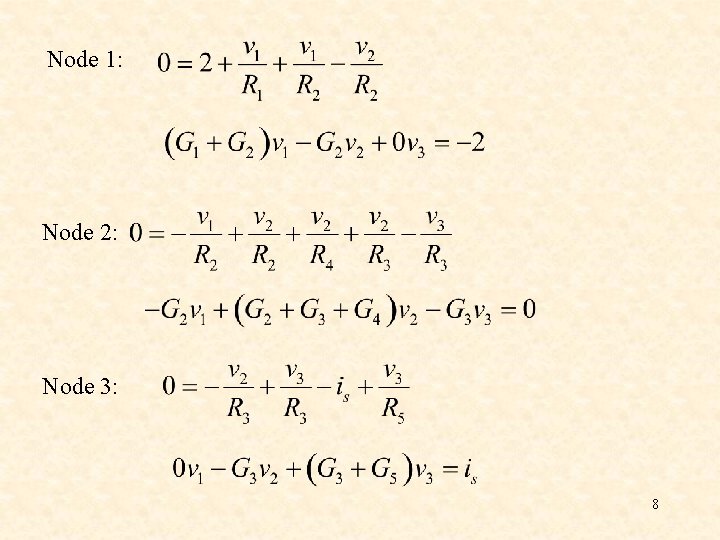
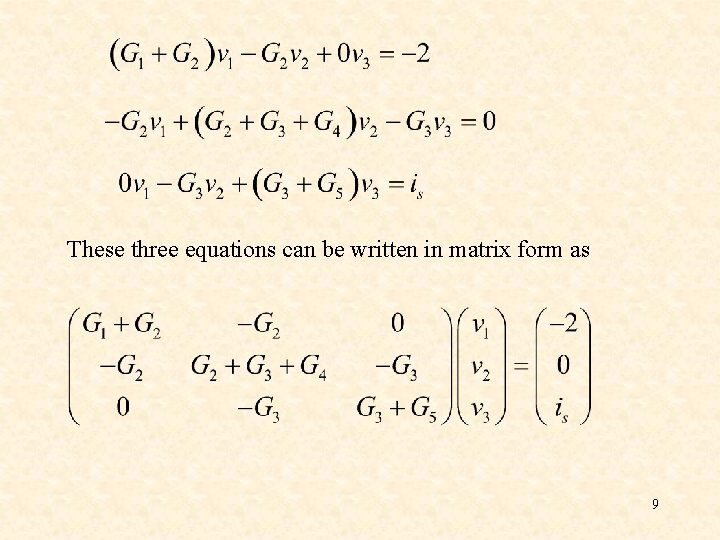


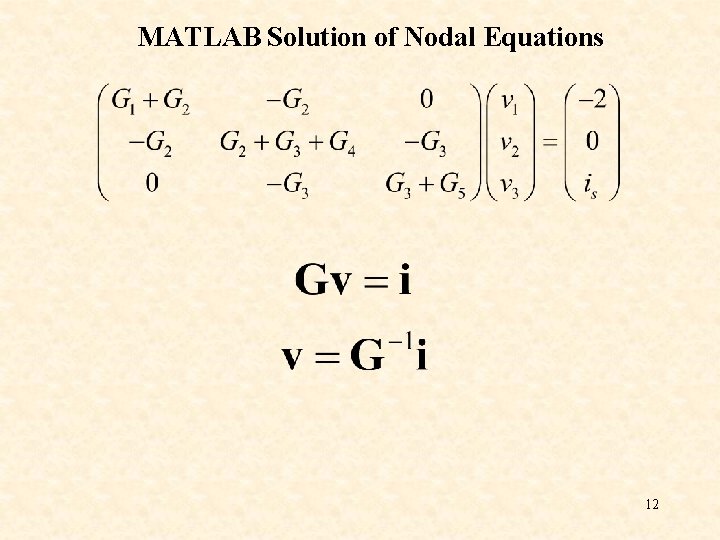






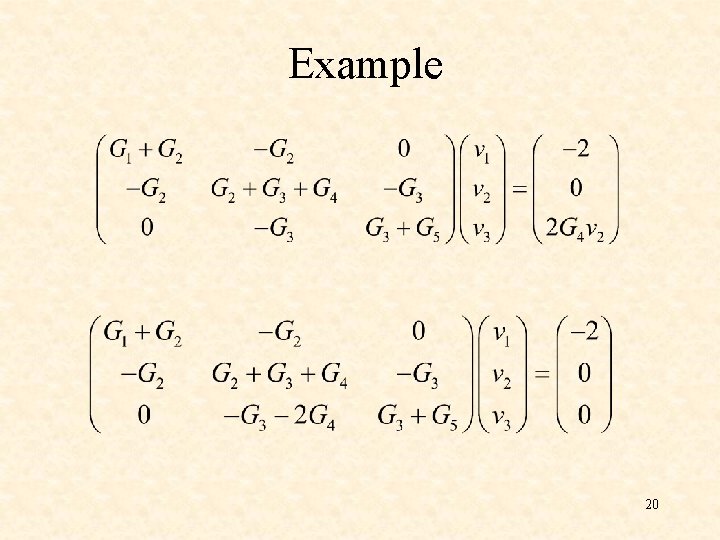
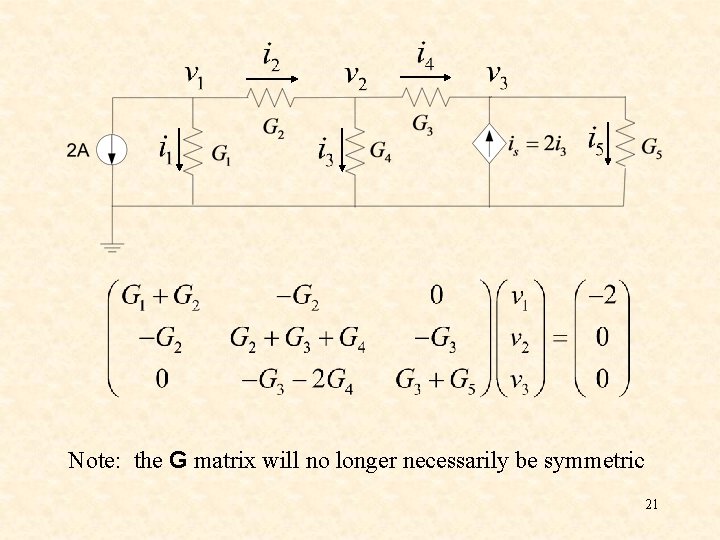


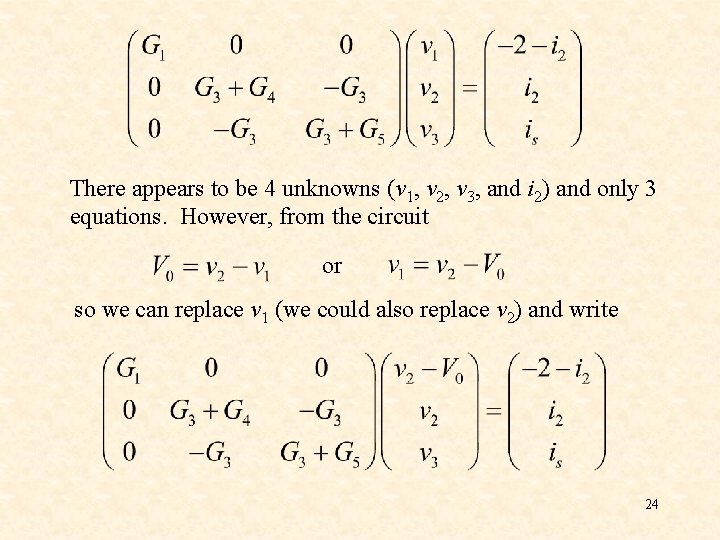




- Slides: 29

Nodal Analysis Discussion D 2. 3 Chapter 2 Section 2 -7 1

Nodal Analysis • Interested in finding the NODE VOLTAGES, which are taken as the variables to be determined • For simplicity we start with circuits containing only current sources 2

Nodal Analysis Steps 1. Select one of the n nodes as a reference node (that we define to be zero voltage, or ground). Assign voltages v 1, v 2, … vn-1 to the remaining n-1 nodes. These voltages are referenced with respect to the reference node. 2. Apply KCL to each of the n-1 non-reference nodes. Use Ohm’s law to express the branch currents in terms of the node voltages. 3. Solve the resulting simultaneous equations to obtain the node voltages v 1, v 2, … vn-1. 3

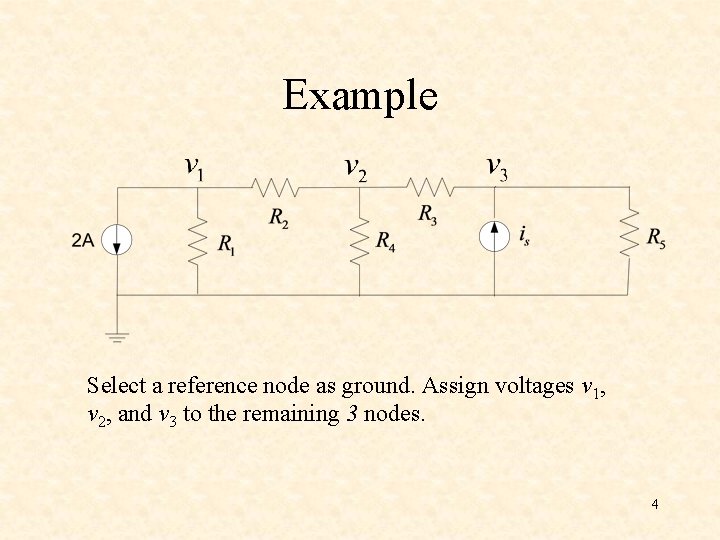
Example Select a reference node as ground. Assign voltages v 1, v 2, and v 3 to the remaining 3 nodes. 4

Example Apply KCL to each of the 3 non-reference nodes (sum of currents leaving node is zero). Node 1: Node 2: Node 3: 5

Example Now express i 1, i 2, …i 5 in terms of v 1, v 2, v 3 (the node voltages). Note that current flows from a higher to a lower potential. 6
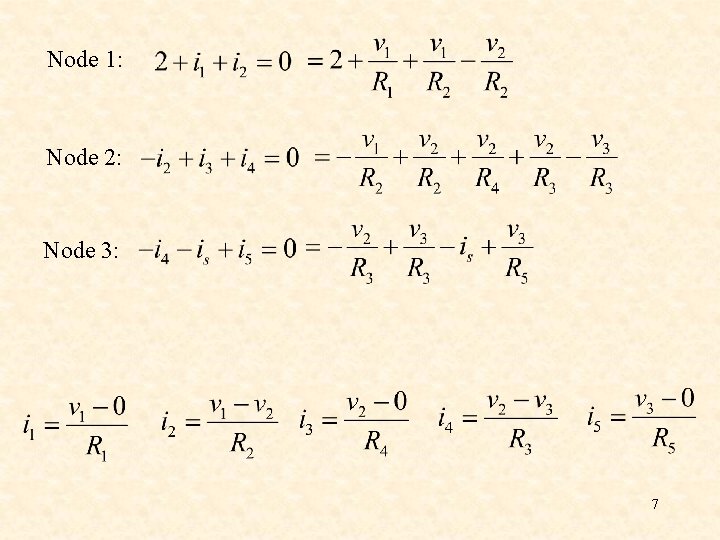
Node 1: Node 2: Node 3: 7
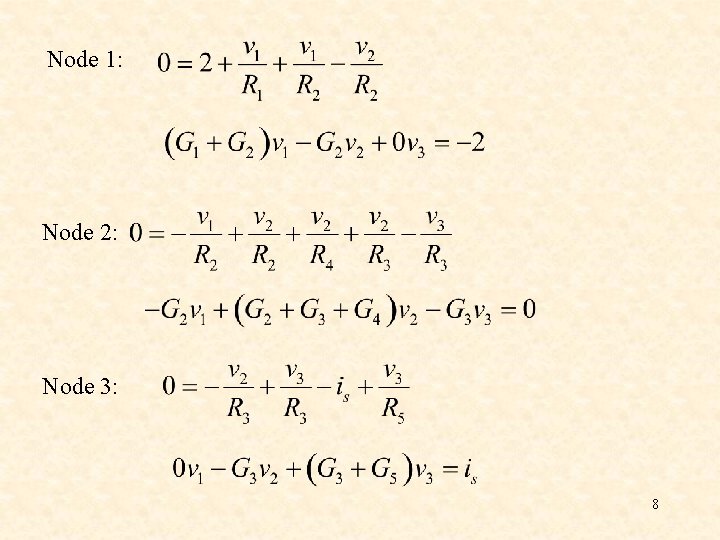
Node 1: Node 2: Node 3: 8
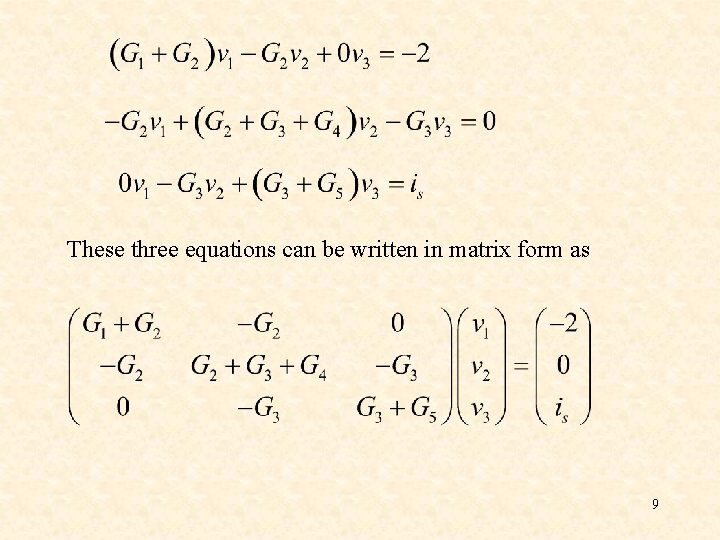
These three equations can be written in matrix form as 9

is an (n – 1) x (n – 1) symmetric conductance matrix is a 1 x (n-1) vector of node voltages is a vector of currents representing “known” currents 10

Writing the Nodal Equations by Inspection • The matrix G is symmetric, gkj = gjk and all of the off-diagonal terms are negative or zero. The gkk terms are the sum of all conductances connected to node k. The gkj terms are the negative sum of the conductances connected to BOTH node k and node j. The ik (the kth component of the vector i) = the algebraic sum of the independent currents connected to node k, with currents entering the 11 node taken as positive.
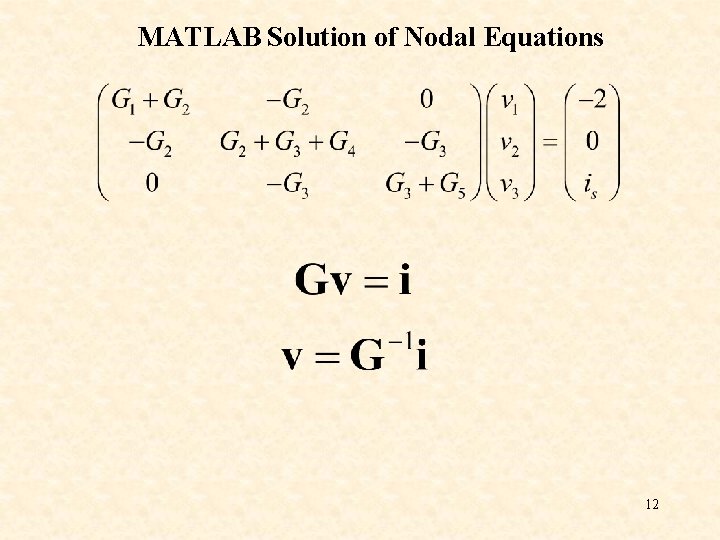
MATLAB Solution of Nodal Equations 12

Test with numbers v 1 v 2 v 3 13

MATLAB Run v 1 v 2 v 3 14

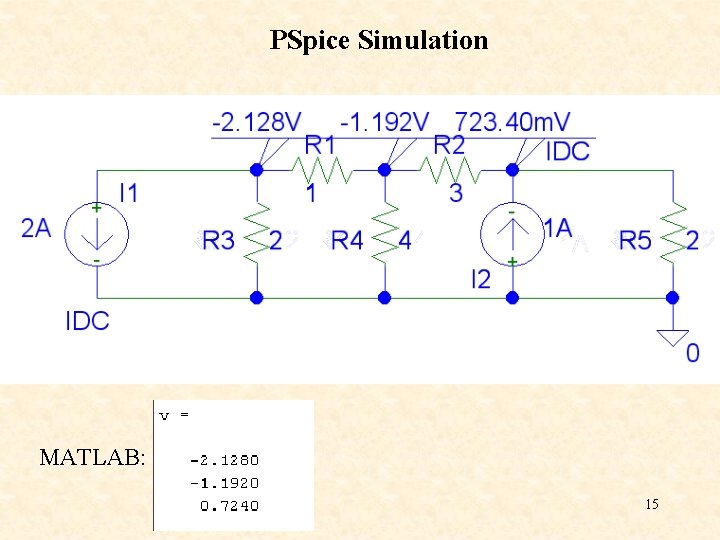
PSpice Simulation MATLAB: 15

What happens if we have dependent current sources in the circuit? 1. Write the nodal equations in the same way we did for circuits with only independent sources. Temporarily, consider the dependent sources as being independent. 2. Express the current of each dependent source in terms of the node voltages. 3. Rewrite the equations with all node voltages on the left hand side of the equality. 16

Example Write nodal equations by inspection. 17

Example 18

Example 19
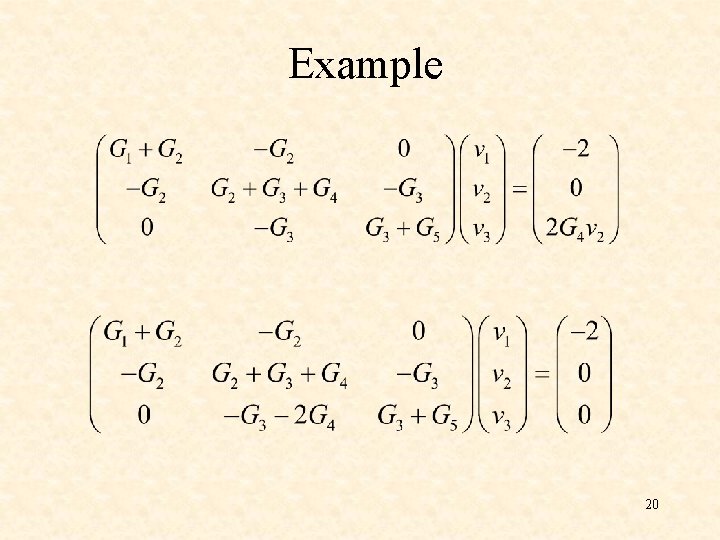
Example 20
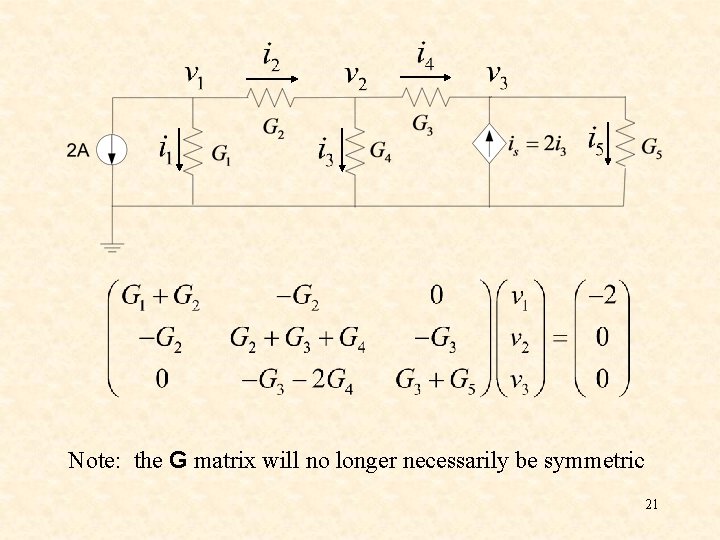
Note: the G matrix will no longer necessarily be symmetric 21

Nodal Analysis for Circuits Containing Voltage Sources That Can’t be Transformed to Current Sources • Case 1. If a voltage source is connected between the reference node and a nonreference node, set the voltage at the nonreference node equal to the voltage of the source. • Case 2. If a voltage source is connected between two nonreference nodes, assume temporarily that through the voltage source is known and write the equations by inspection. 22

Example Assume temporarily that i 2 is known and write the equations by inspection. 23
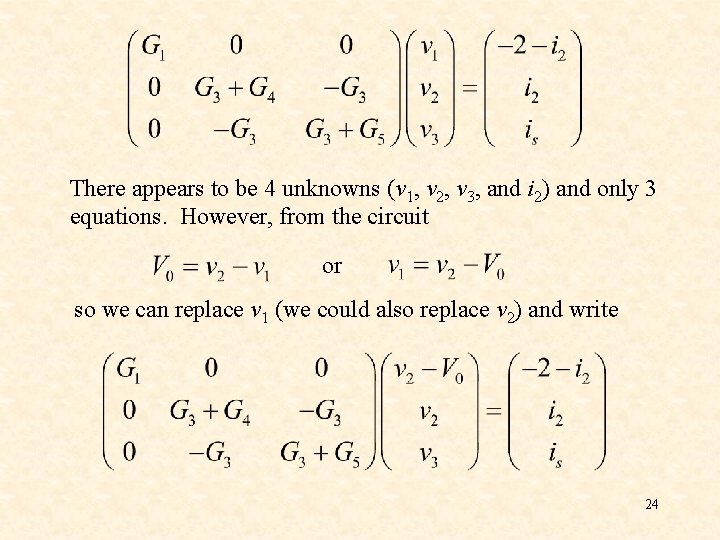
There appears to be 4 unknowns (v 1, v 2, v 3, and i 2) and only 3 equations. However, from the circuit or so we can replace v 1 (we could also replace v 2) and write 24

Writing the above equation with the unknowns (v 2, v 3, i 2) on the LHS yields 25

Test with numbers v 1 v 2 v 3 Noting that 26

Test with numbers v 1 v 2 v 3 Unknowns: 27

MATLAB Run v 1 V V A v 2 v 3 i 2 v 3 28

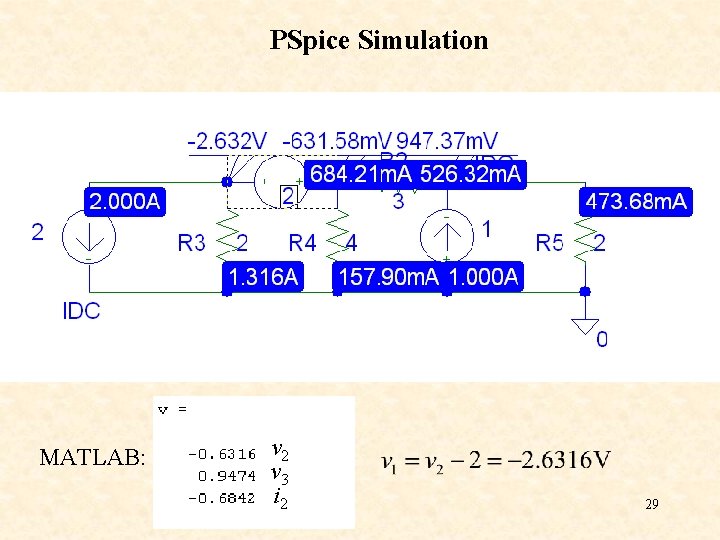
PSpice Simulation MATLAB: v 2 v 3 i 2 29