No Regret Algorithms in Games Georgios Piliouras Georgia

No Regret Algorithms in Games Georgios Piliouras Georgia Institute of Technology John Hopkins University

No Regret Algorithms in Games Georgios Piliouras Georgia Institute of Technology John Hopkins University

No Regret Algorithms in Games Georgios Piliouras Georgia Institute of Technology John Hopkins University

No Regret Algorithms in Social Interactions Georgios Piliouras Georgia Institute of Technology John Hopkins University

No Regret Algorithms in Social Interactions Georgios Piliouras Georgia Institute of Technology John Hopkins University

No Regret Behavior in Social Interactions Georgios Piliouras Georgia Institute of Technology John Hopkins University

No Regret Behavior in Social Interactions Georgios Piliouras Georgia Institute of Technology John Hopkins University

“Reasonable” Behavior in Social Interactions Georgios Piliouras Georgia Institute of Technology John Hopkins University

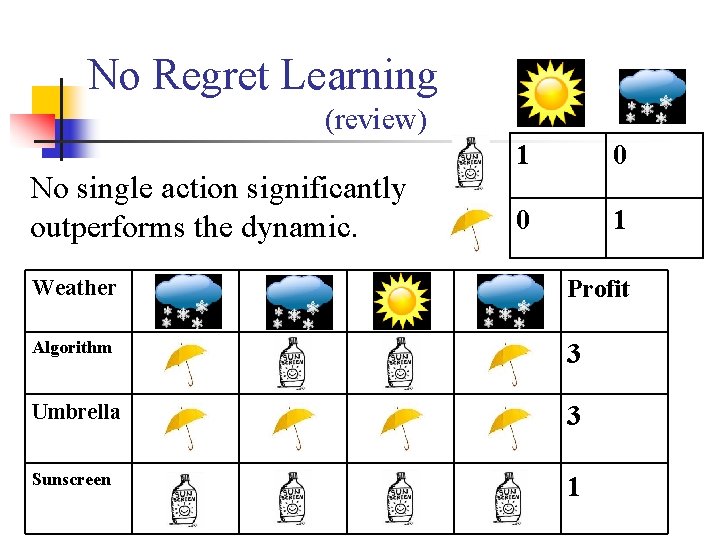
No Regret Learning (review) No single action significantly outperforms the dynamic. n 1 0 0 1 Regret(T) in a history of T periods: total profit of best fixed action in hindsight - total profit of algorithm An algorithm is characterized as “no regret” if for every input sequence the regret grows sublinearly in T. [Blackwell 56], [Hannan 57], [Fundberg, Levine 94], …

No Regret Learning (review) No single action significantly outperforms the dynamic. 1 0 0 1 Weather Profit Algorithm 3 Umbrella 3 Sunscreen 1

Games (i. e. Social Interactions) n n n Interacting entities Pursuing their own goals Lack of centralized control

Games (review) n n players Set of strategies Si for each player i n Possible states (strategy profiles) S=×Si n Utility ui: S→R n n n Social Welfare Q: S→R Extend to allow probabilities Δ(Si), Δ(S) ui(Δ(S))=E(ui(S)) Q(Δ(S))=E(Q(S))

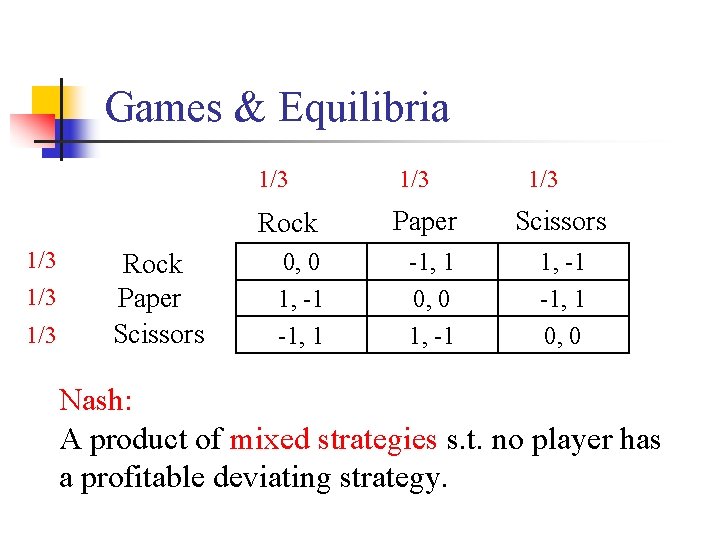
Games & Equilibria 1/3 1/3 1/3 Rock Paper Scissors 0, 0 1, -1 -1, 1 0, 0 Nash: A product of mixed strategies s. t. no player has a profitable deviating strategy.

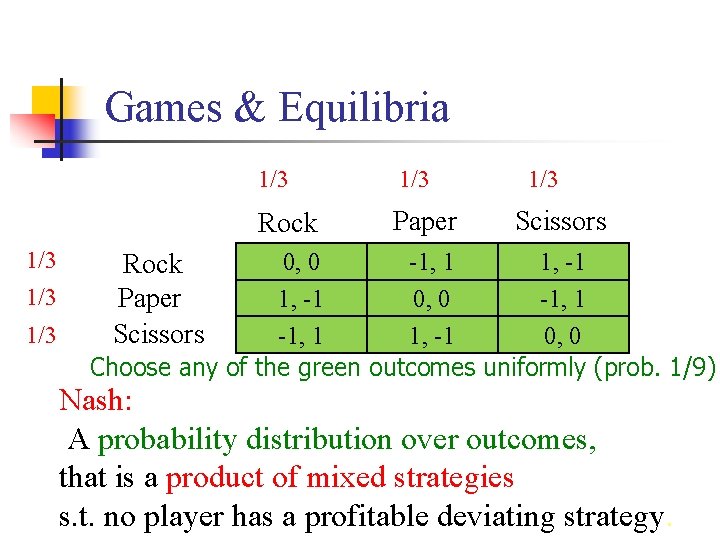
Games & Equilibria 1/3 1/3 1/3 Rock Paper 1/3 Scissors 0, 0 -1, 1 1, -1 0, 0 Choose any of the green outcomes uniformly (prob. 1/9) Rock Paper Scissors Nash: A probability distribution over outcomes, that is a product of mixed strategies s. t. no player has a profitable deviating strategy.

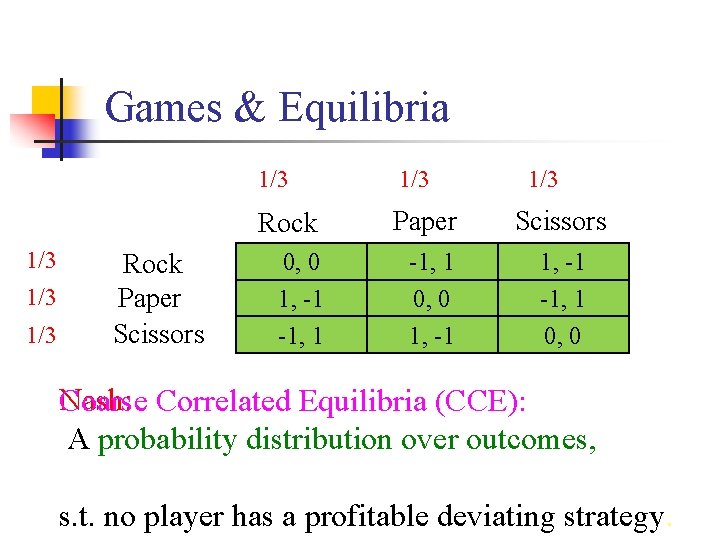
Games & Equilibria 1/3 1/3 1/3 Rock Paper Scissors 0, 0 1, -1 -1, 1 0, 0 Nash: Coarse Correlated Equilibria (CCE): A probability distribution over outcomes, s. t. no player has a profitable deviating strategy.

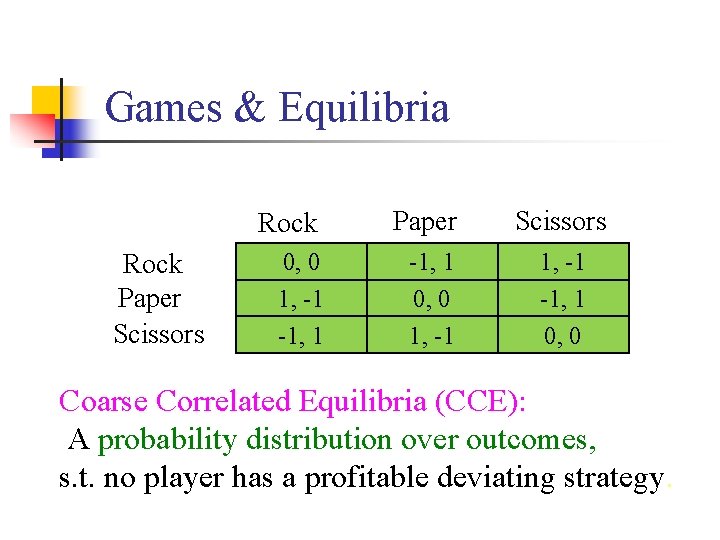
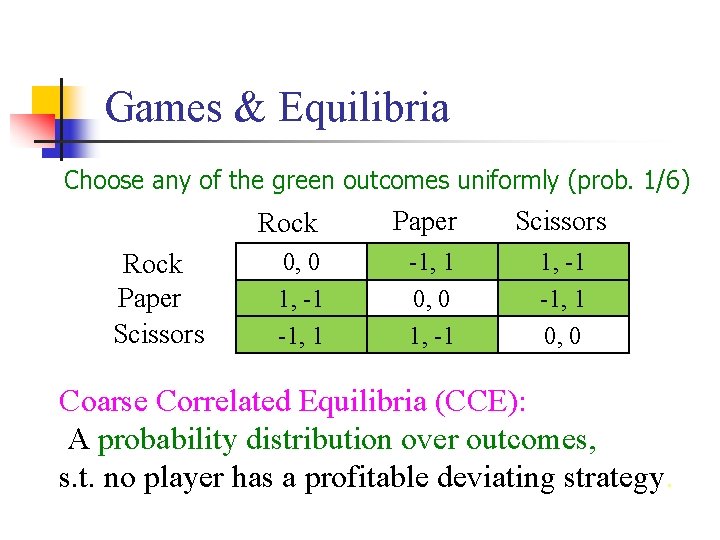
Games & Equilibria Rock Paper Scissors 0, 0 1, -1 -1, 1 0, 0 Coarse Correlated Equilibria (CCE): A probability distribution over outcomes, s. t. no player has a profitable deviating strategy.

Games & Equilibria Choose any of the green outcomes uniformly (prob. 1/6) Rock Paper Scissors 0, 0 1, -1 -1, 1 0, 0 Coarse Correlated Equilibria (CCE): A probability distribution over outcomes, s. t. no player has a profitable deviating strategy.

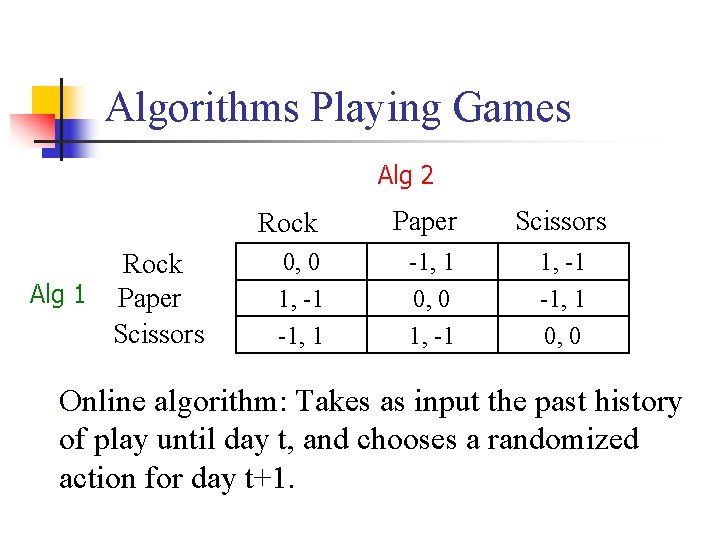
Algorithms Playing Games Alg 2 Rock Alg 1 Paper Scissors Rock Paper Scissors 0, 0 1, -1 -1, 1 0, 0 . Online algorithm: Takes as input the past history of play until day t, and chooses a randomized action for day t+1.

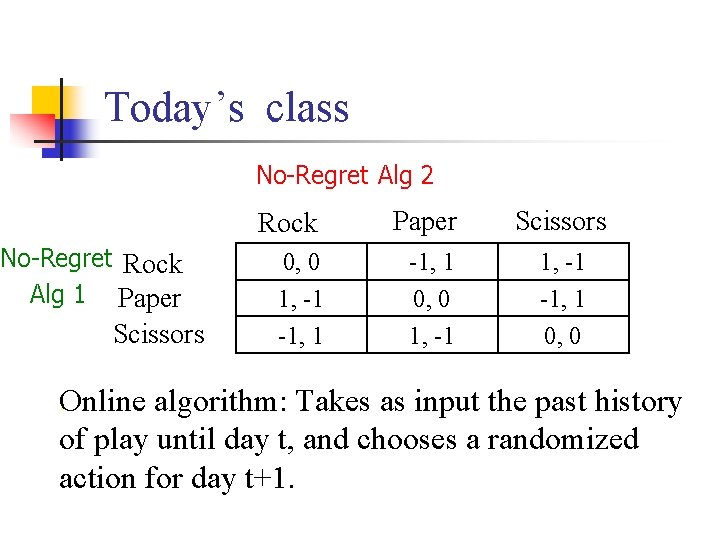
Today’s class No-Regret Alg 2 No-Regret Rock Alg 1 Paper Scissors Rock Paper Scissors 0, 0 1, -1 -1, 1 0, 0 . Online algorithm: Takes as input the past history of play until day t, and chooses a randomized action for day t+1.

No Regret Algorithms & CCE n A history of no-regret n algorithms is a sequence of outcomes s. t. no agent has a single deviating action that can increase her average payoff. A Coarse Correlated Equilibrium is a probability distribution over outcomes s. t. no agent has a single deviating action that can increase her expected payoff.

How good are the CCE? n n n It depends… Which class of games are we interested in? Which notion of social welfare? Today Class of games: potential games Social welfare: makespan [Kleinberg, P. , Tardos STOC 09]

Congestion Games n n n players and m resources (“edges”) Each strategy corresponds to a set of resources (“paths”) Each edge has a cost function ce(x) that determines the cost as a function on the # of players using it. Cost experienced by a player = sum of edge costs Cost(red)=6 Cost(green)=8 x x 2 x

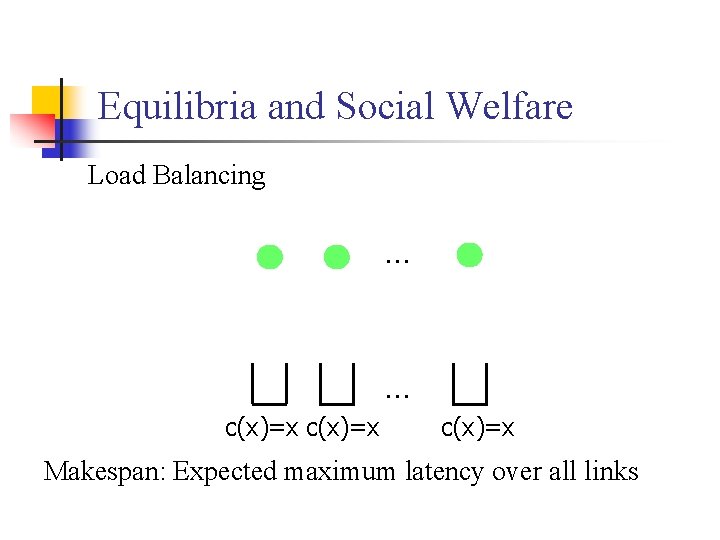
Equilibria and Social Welfare Load Balancing … … c(x)=x Makespan: Expected maximum latency over all links

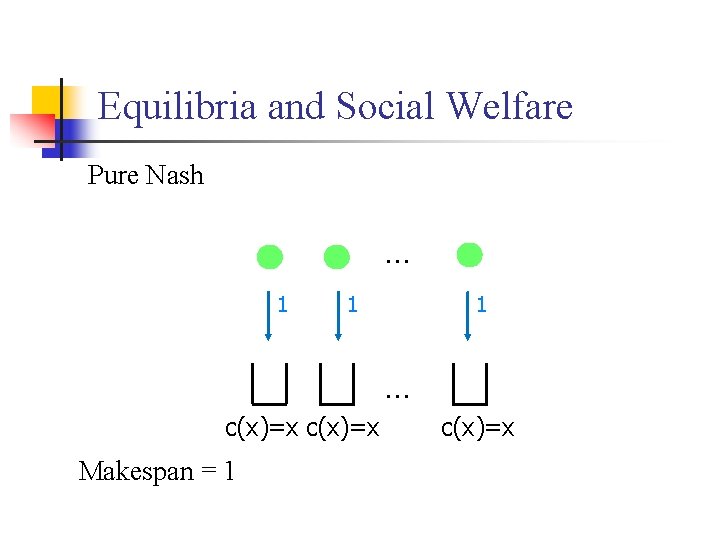
Equilibria and Social Welfare Pure Nash … 1 1 1 … c(x)=x Makespan = 1 c(x)=x

Equilibria and Social Welfare (Mixed) Nash … 1/n 1/n … c(x)=x Θ(logn/loglogn) > 1 Makespan = Ω(logn/loglogn) [Koutsoupias, Mavronicolas, Spirakis ’ 02], [Czumaj, Vöcking ’ 02]

Equilibria and Social Welfare Coarse Correlated Equilibria … … c(x)=x Makespan = Ω(√n) >> Θ(logn/loglogn) [Blum, Hajiaghayi, Ligett, Roth ’ 08]

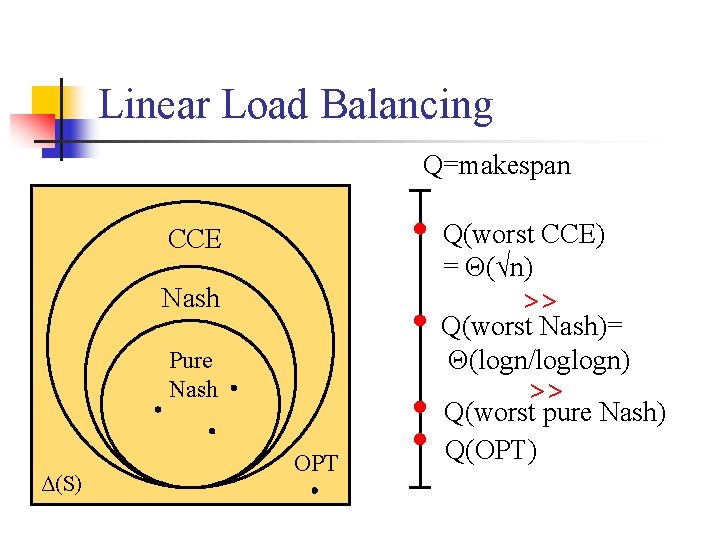
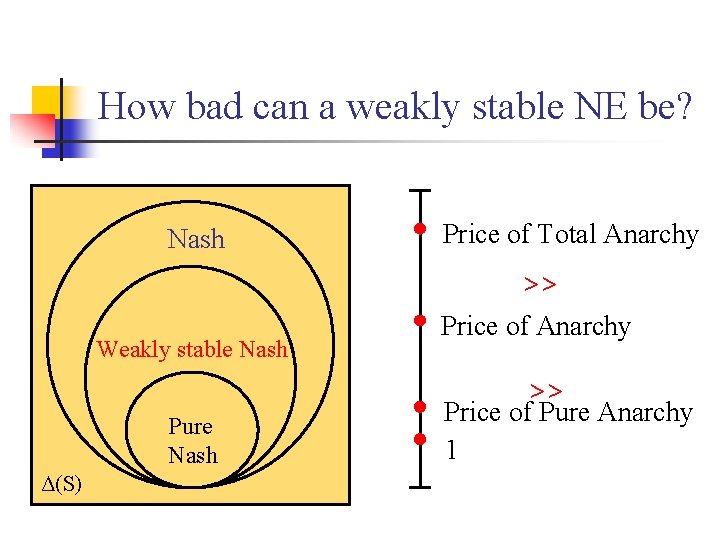
Linear Load Balancing Q=makespan Q(worst CCE) = Θ(√n) CCE Nash >> Q(worst Nash)= Θ(logn/loglogn) Pure Nash Δ(S) >> OPT Q(worst pure Nash) Q(OPT)

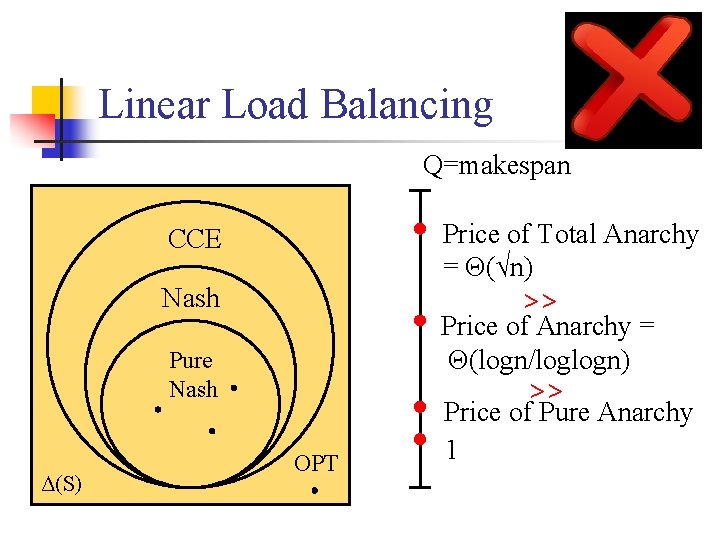
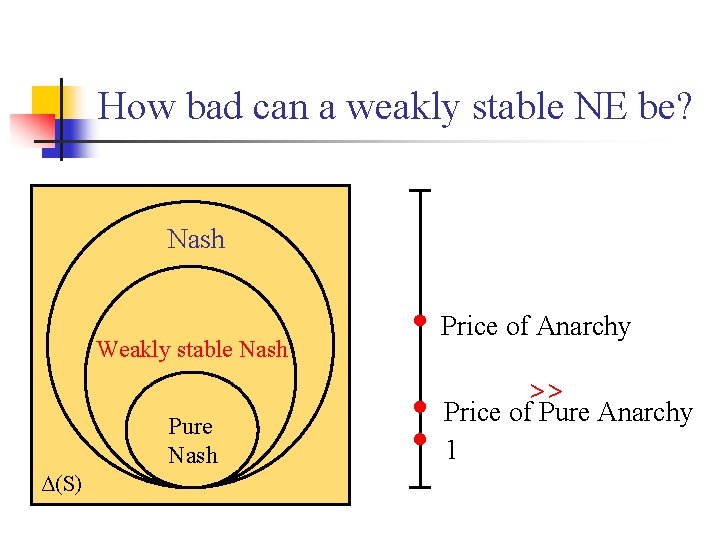
Linear Load Balancing Q=makespan Price of Total Anarchy = Θ(√n) CCE Nash >> Price of Anarchy = Θ(logn/loglogn) Pure Nash Δ(S) >> OPT Price of Pure Anarchy 1

Our Hope Natural no-regret algorithms should be able to steer away from worst case equilibria.

The Multiplicative Weights Algorithm (MWA) [Littlestone, Warmuth ’ 94], [Freund, Schapire ‘ 99] n Pick s with probability proportional to (1 -ε)total(s), where total(s) denotes combined cost in all past periods. Provable performance guarantees against arbitrary opponents No Regret: Against any sequence of opponents’ play, avg. payoff converges to that of the best fixed option (or better). n

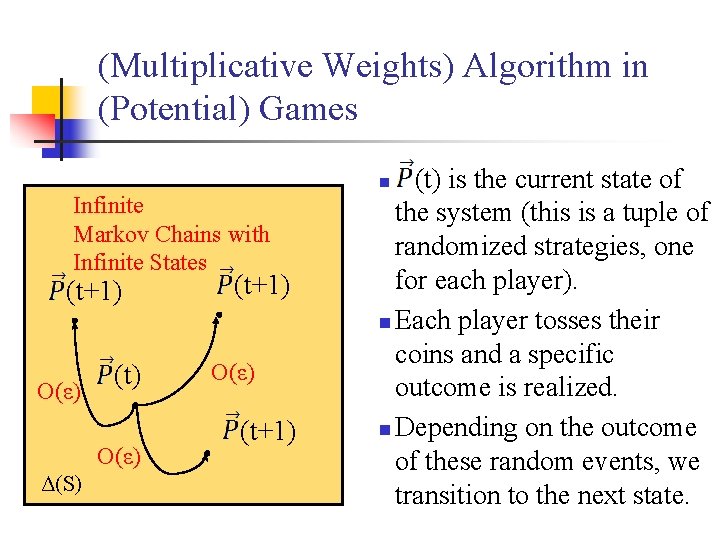
(Multiplicative Weights) Algorithm in (Potential) Games (t) is the current state of the system (this is a tuple of randomized strategies, one for each player). n Each player tosses their coins and a specific outcome is realized. n Depending on the outcome of these random events, we transition to the next state. n Infinite Markov Chains with Infinite States (t+1) O(ε) (t) O(ε) Δ(S) (t+1) O(ε) (t+1)

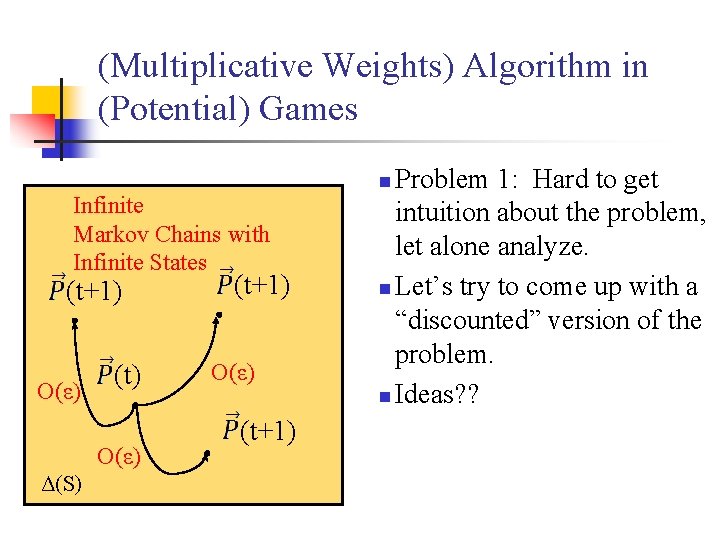
(Multiplicative Weights) Algorithm in (Potential) Games Infinite Markov Chains with Infinite States (t+1) O(ε) (t) O(ε) Δ(S) (t+1) O(ε) (t+1) Problem 1: Hard to get intuition about the problem, let alone analyze. n Let’s try to come up with a “discounted” version of the problem. n Ideas? ? n

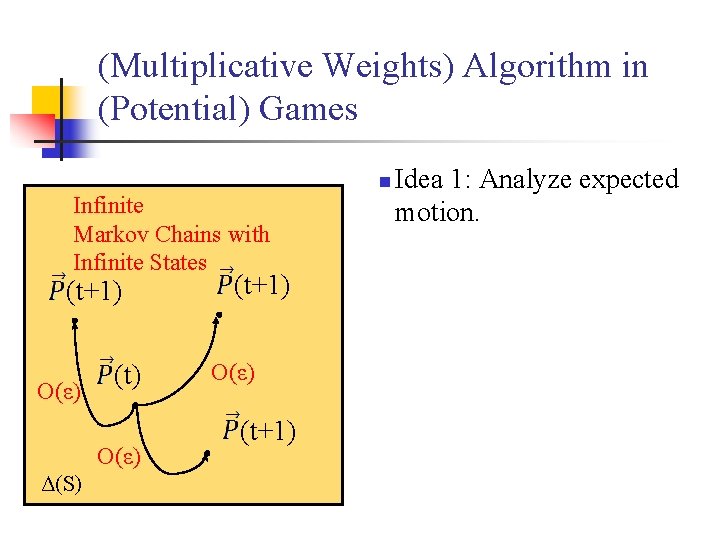
(Multiplicative Weights) Algorithm in (Potential) Games Infinite Markov Chains with Infinite States (t+1) O(ε) (t) O(ε) Δ(S) (t+1) O(ε) (t+1) n Idea 1: Analyze expected motion.

(Multiplicative Weights) Algorithm in (Potential) Games n n E[ (t+1)] (t) The system evolution is now deterministic. (i. e. there exists a function f, s. t. E[ (t+1)]= f ( (t), ε ) O(ε) n Δ(S) Idea 1: Analyze expected motion. I wish to analyze this function (e. g. find fixed points).

(Multiplicative Weights) Algorithm in (Potential) Games Problem 2: The function f is still rather complicated. n Idea 2: I wish to analyze the MWA dynamics for small ε. n Use Taylor expansion to find a first order approximation to f. n E[ (t+1)] (t) Δ(S) O(ε) f ( (t), ε) = f ( (t), 0) + ε ×f ´( (t), 0) + O(ε 2)

(Multiplicative Weights) Algorithm in (Potential) Games Problem 2: The function f is still rather complicated. n Idea 2: I wish to analyze the MWA dynamics for small ε. n Use Taylor expansion to find a first order approximation to f. n E[ (t+1)] (t) Δ(S) O(ε) f ( (t), ε) ≈ f ( (t), 0) + ε ×f ´( (t), 0)

(Multiplicative Weights) Algorithm in (Potential) Games n (t) Δ(S) f´( (t), 0) As ε→ 0, the equation f ( (t), ε)-f ( (t), 0) = f´( (t), 0) ε specifies a vector on each point of our state space (i. e. a vector field). This vector field defines a system of ODEs which we are going to analyze.

(Multiplicative Weights) Algorithm in (Potential) Games n (t) Δ(S) f´( (t), 0) As ε→ 0, the equation f ( (t), ε)-f ( (t), 0) = f´( (t), 0) ε specifies a vector on each point of our state space (i. e. a vector field). This vector field defines a system of ODEs which we are going to analyze.

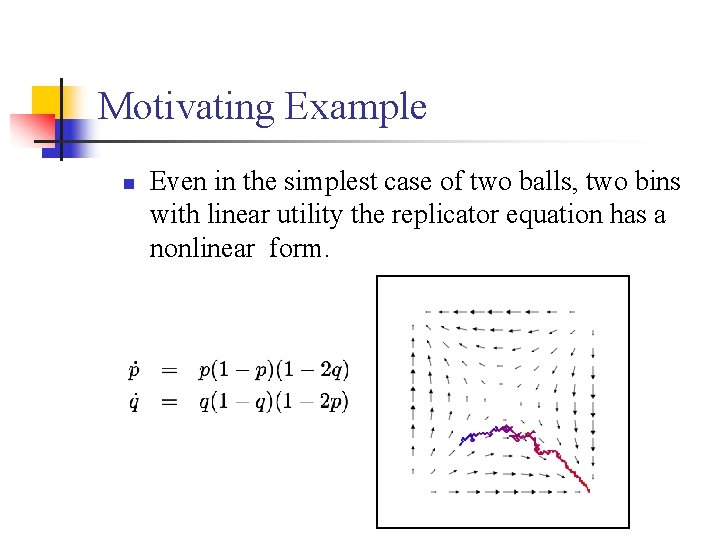
Deriving the ODE n Taking expectations: n Differentiate w. r. t. ε, take expected value: n This is the replicator dynamic studied in evolutionary game theory.

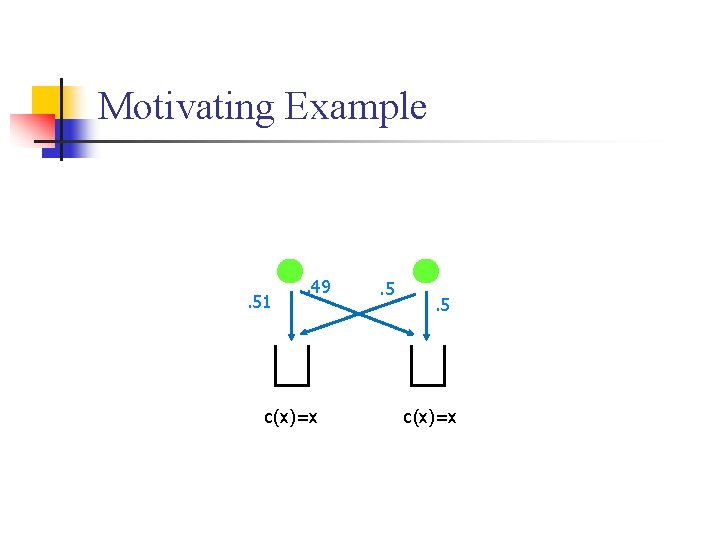
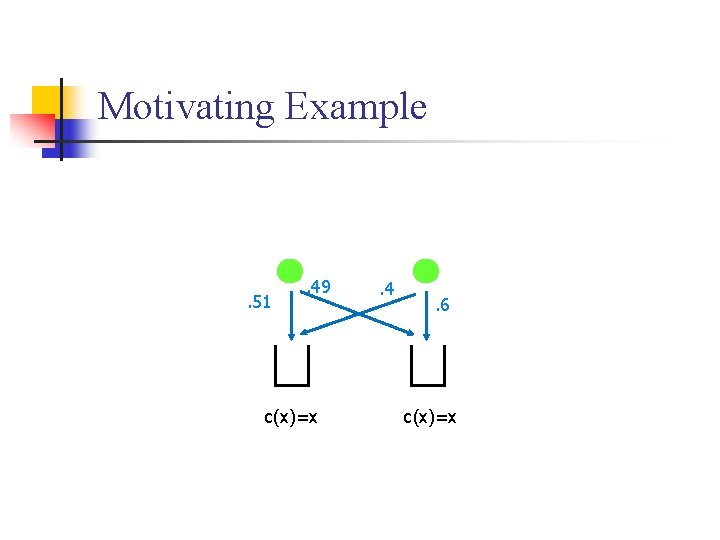
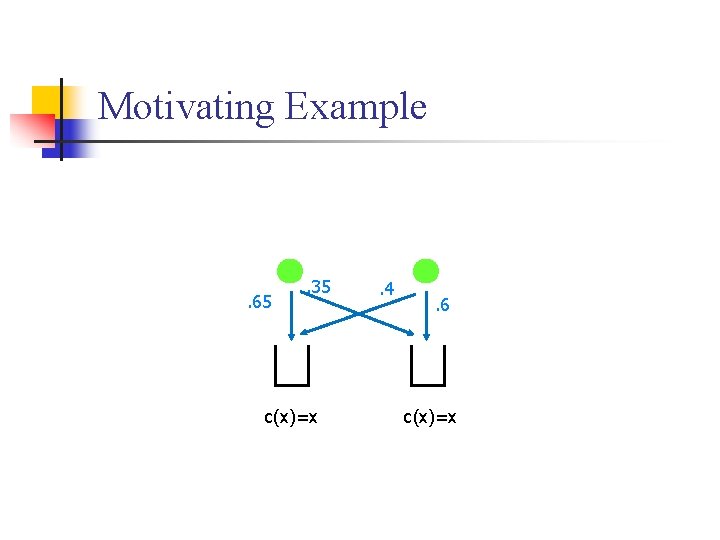
Motivating Example c(x)=x

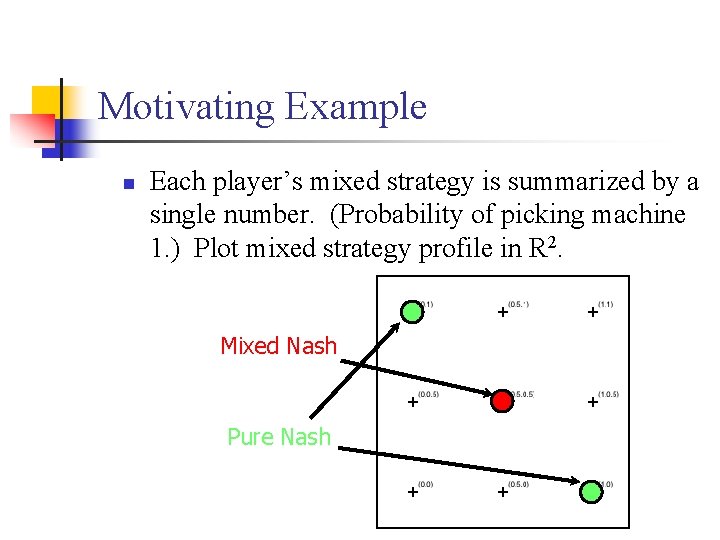
Motivating Example n Each player’s mixed strategy is summarized by a single number. (Probability of picking machine 1. ) Plot mixed strategy profile in R 2. Mixed Nash Pure Nash

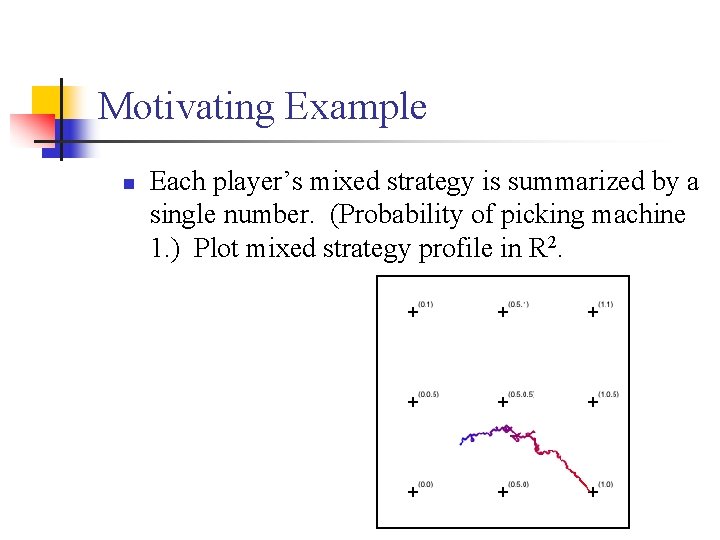
Motivating Example n Each player’s mixed strategy is summarized by a single number. (Probability of picking machine 1. ) Plot mixed strategy profile in R 2.

Motivating Example n Even in the simplest case of two balls, two bins with linear utility the replicator equation has a nonlinear form.

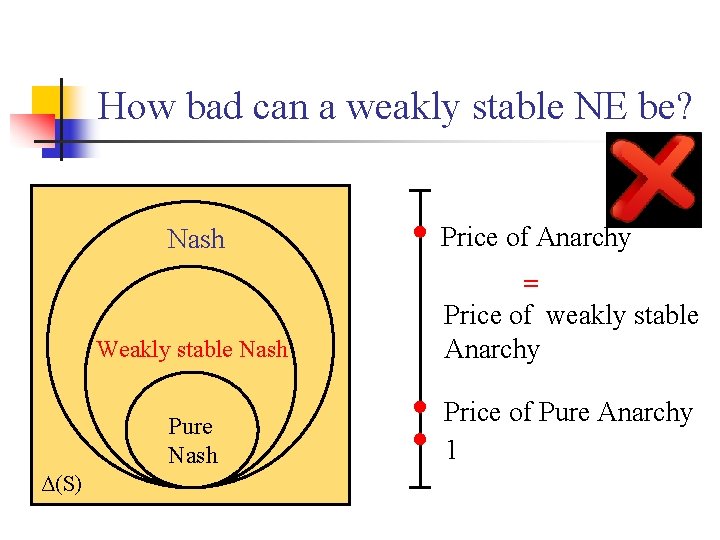
The potential function n The congestion game has a potential function n Let Ψ=E[Φ]. A calculation yields n Hence Ψ decreases except when every player randomizes over paths of equal expected cost (i. e. is a Lyapunov function of the dynamics). [Monderer -Shapley ’ 96].

Unstable vs. stable fixed points The derivative of ξ is a matrix J (the Jacobian) whose spectrum distinguishes stable from unstable fixed points. Unstable if some eigenvalue has positive real part, else neutrally stable. Non-Nash fixed points are unstable. (Easy) Which Nash are unstable? n • •

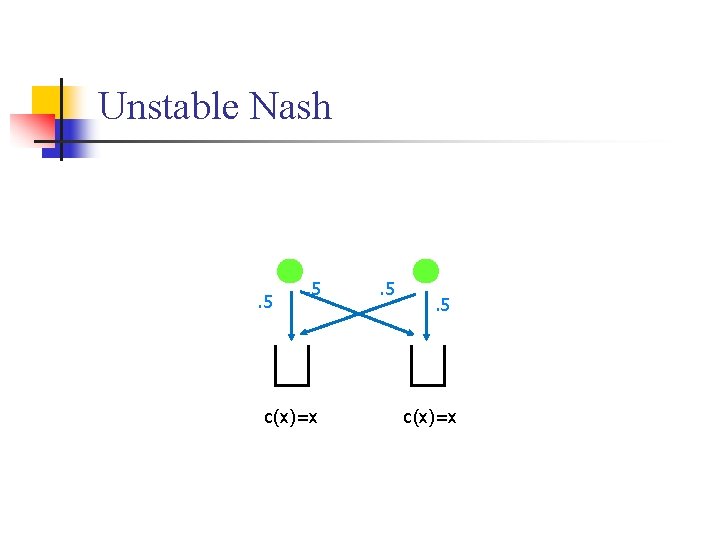
Unstable Nash . 5 . 5 c(x)=x

Motivating Example . 51 . 49 c(x)=x . 5 c(x)=x

Motivating Example . 51 . 49 c(x)=x . 4 . 6 c(x)=x

Motivating Example . 65 . 35 c(x)=x . 4 . 6 c(x)=x

Unstable vs. stable fixed points The derivative of ξ is a matrix J (the Jacobian) whose spectrum distinguishes stable from unstable fixed points. Unstable if some eigenvalue has positive real part, else neutrally stable. Non-Nash fixed points are unstable. (Easy) Which Nash are unstable? n • •

Unstable vs. stable Nash n n n Jp submatrix of J of strategies with positive prob. Every eigenvalue of Jp is an eigenvalue of J. Computing the entries of Jp reveals that at Nash, If Tr(Jp)=0 and no eigenvalue has positive real part, then they all are pure imaginary, so Tr(Jp 2) ≤ 0. But clearly Tr(Jp 2) ≥ 0. Hence E[costi(R, Q, s-i, j)] = E[costi(R’, Q, s-i, j)] whenever pi. R, pi. R’, pj. Q’>0. ∴ A new refinement of Nash equilibria!

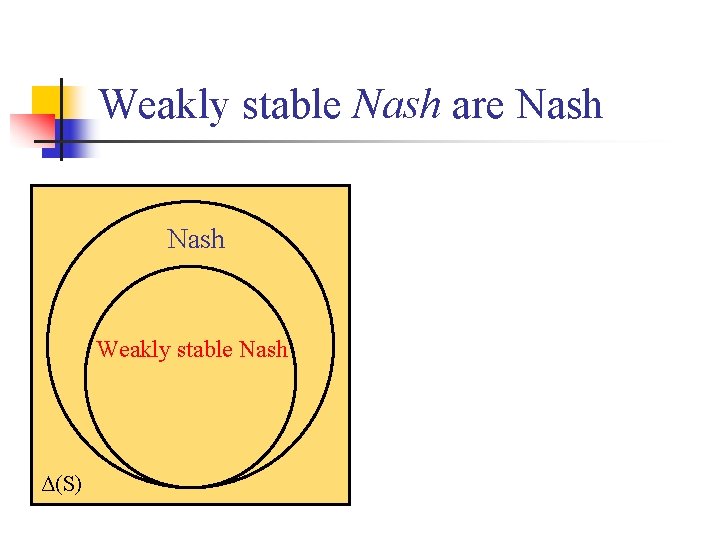
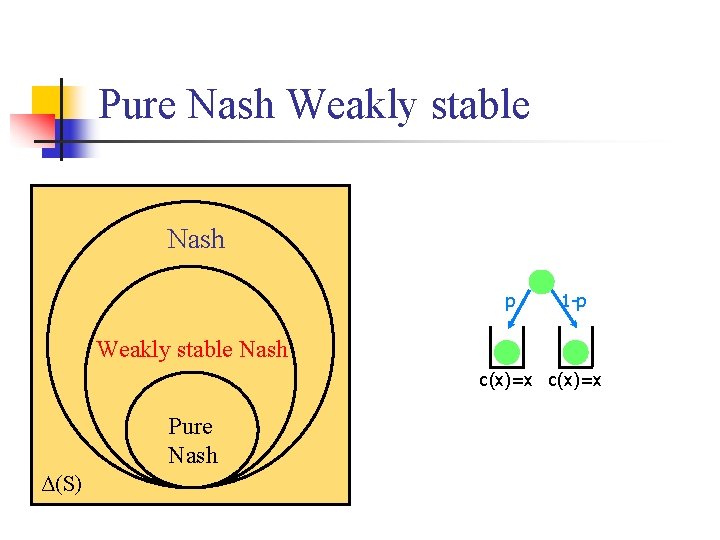
Weakly stable Nash equilibrium n Definition: A weakly stable Nash equilibrium is a mixed Nash equilibrium (σ1, . . . , σn) such that: n for all players i, j. . . n if i switches to using any pure strategy in support(σi). . . n then j remains indifferent between all the strategies in support(σj).

Weakly stable Nash are Nash Weakly stable Nash Δ(S)

Weakly stable Nash equilibrium n Definition: A weakly stable Nash equilibrium is a mixed Nash equilibrium (σ1, . . . , σn) such that: n for all players i, j. . . n if i switches to using any pure strategy in support(σi). . . n then j remains indifferent between all the strategies in support(σj).

Pure Nash Weakly stable Nash p 1 -p Weakly stable Nash c(x)=x Pure Nash Δ(S)

How bad can a weakly stable NE be? Nash Price of Total Anarchy >> Weakly stable Nash Price of Anarchy >> Pure Nash Δ(S) Price of Pure Anarchy 1

How bad can a weakly stable NE be? Nash Weakly stable Nash Price of Anarchy >> Pure Nash Δ(S) Price of Pure Anarchy 1

How bad can a weakly stable NE be? Nash Price of Anarchy = Δ(S) Weakly stable Nash Price of weakly stable Anarchy Pure Nash Price of Pure Anarchy 1

Mixed weakly stable NE are due to rare coincidences Example: p 1 -p c(x)=x Relies on a coincidence: two edges having equal cost functions. n If we perturb the cost functions — e. g. scale each one by an independent random factor between 1 -δ and 1+δ — then the game has no mixed equilibrium with the same support sets. n

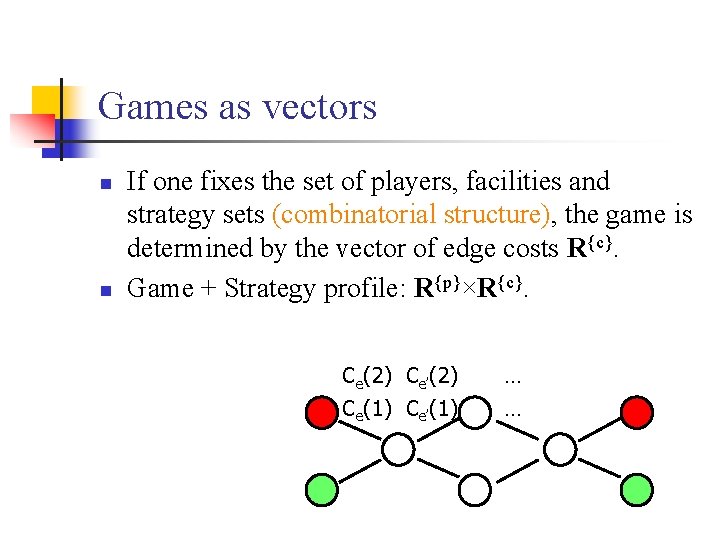
Games as vectors n n If one fixes the set of players, facilities and strategy sets (combinatorial structure), the game is determined by the vector of edge costs R{c}. Game + Strategy profile: R{p}×R{c}. Ce(2) Ce’(2) Ce(1) Ce’(1) … …

Weakly Stable Nash Restrictions The assertion {pi. R}iεN, RεP(i) is a fully mixed weakly stable eq. of the game with edge costs {ce(x)}eεE, 1≤x≤n entails many equations among {pi}, {ce(x)}: These are all polynomial equations. (In fact, multilinear. ) Do they imply a nonzero polynomial equation among {ce(x)}?

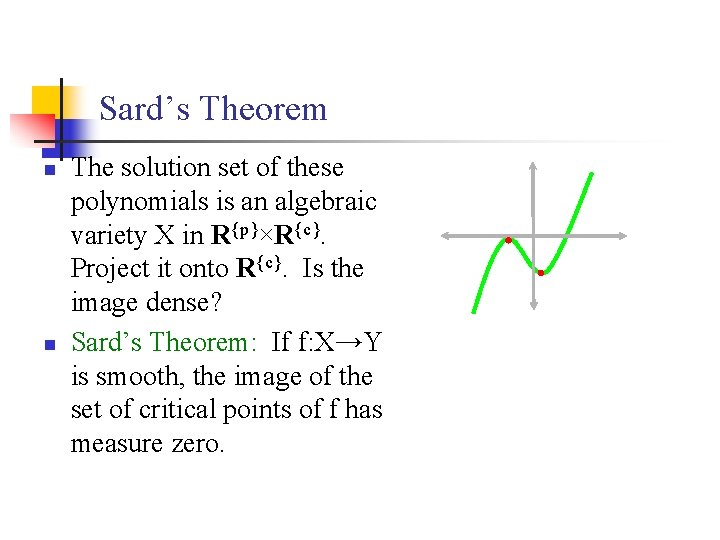
Sard’s Theorem n n The solution set of these polynomials is an algebraic variety X in R{p}×R{c}. Project it onto R{c}. Is the image dense? Sard’s Theorem: If f: X→Y is smooth, the image of the set of critical points of f has measure zero.

Sard’s Theorem n n The solution set of these polynomials is an algebraic variety X in R{p}×R{c}. Project it onto R{c}. Is the image dense? Sard’s Theorem: If f: X→Y Use an alg. geom. version is smooth, the image of the of Sard’s Theorem and set of critical points of f has prove the derivative of f is measure zero. rank-deficient everywhere.

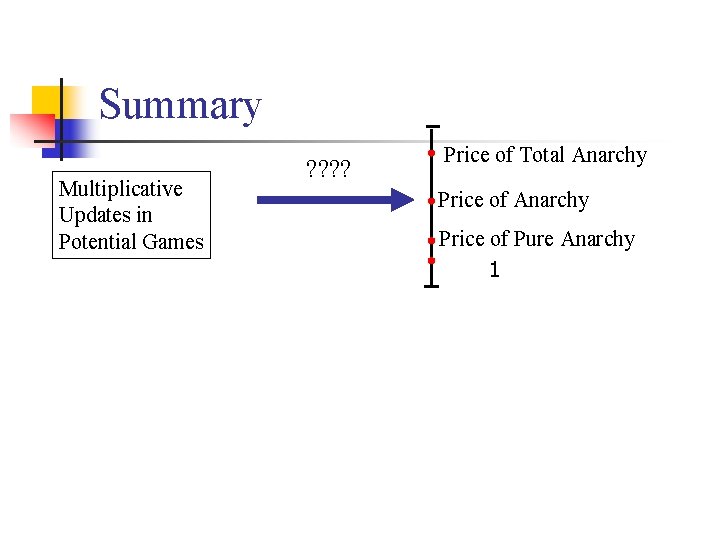
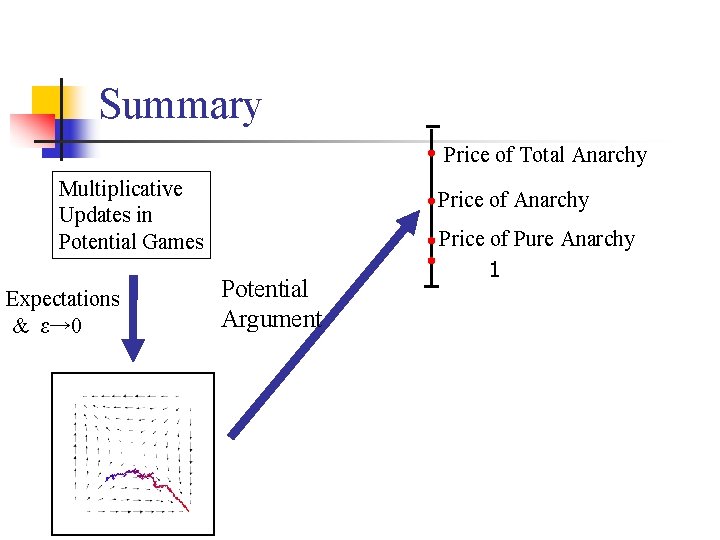
Summary Multiplicative Updates in Potential Games ? ? Price of Total Anarchy Price of Pure Anarchy 1

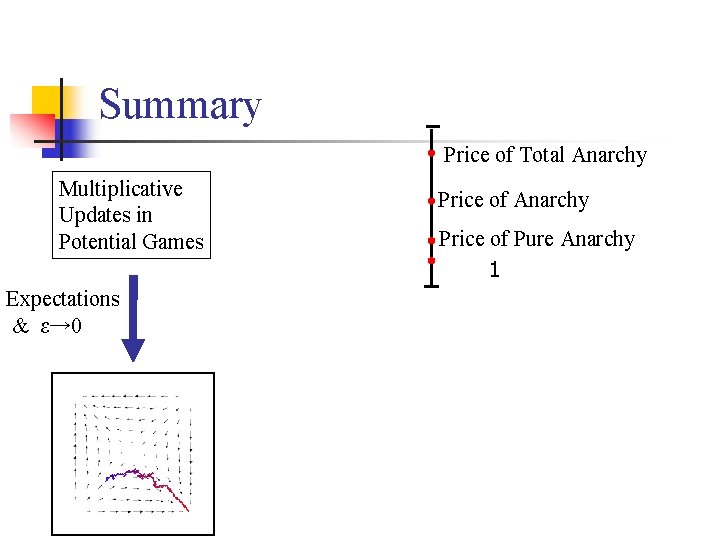
Summary Price of Total Anarchy Multiplicative Updates in Potential Games Expectations & ε→ 0 Price of Anarchy Price of Pure Anarchy 1

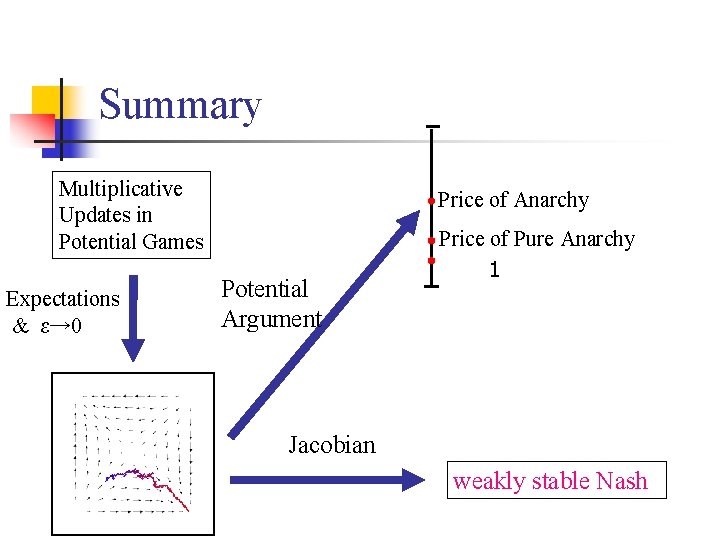
Summary Price of Total Anarchy Multiplicative Updates in Potential Games Expectations & ε→ 0 Price of Anarchy Potential Argument Price of Pure Anarchy 1

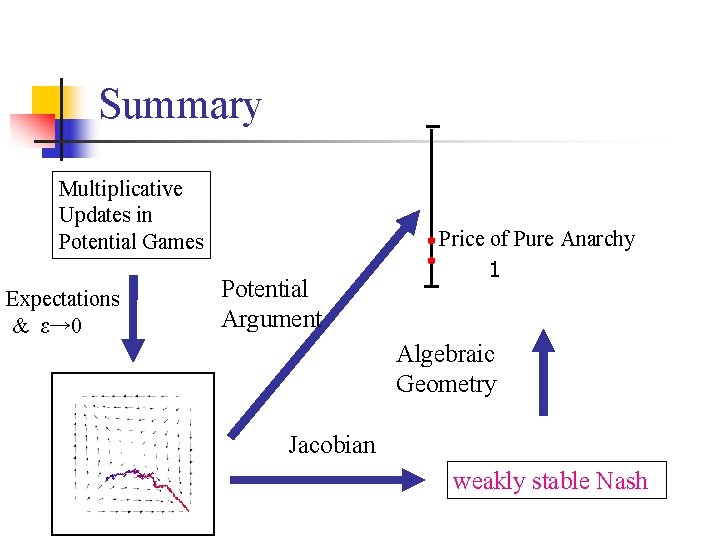
Summary Multiplicative Updates in Potential Games Expectations & ε→ 0 Price of Anarchy Potential Argument Price of Pure Anarchy 1 Jacobian weakly stable Nash

Summary Multiplicative Updates in Potential Games Expectations & ε→ 0 Potential Argument Price of Pure Anarchy 1 Algebraic Geometry Jacobian weakly stable Nash

[Kleinberg, P. , Tardos STOC 09] Summary Taylor Series Manipulations Multiplicative Updates in Potential Games Expectations & ε→ 0 Potential Argument Price of Pure Anarchy 1 Algebraic Geometry Jacobian weakly stable Nash

Learning Algs + Social Welfare n n n How low can we go? [Kleinberg, P. , Tardos STOC 09] [Roughgarden STOC 09] Any no-regret alg in potential games, when social welfare is the sum of utilities. Price of Anarchy Price of Pure Anarchy

Learning Algs + Social Welfare How low can we go? n [Kleinberg, P. , Tardos STOC 09] n [Roughgarden STOC 09] n [Balcan, Blum, Mansour ICS 2010] In specific classes of potential games via public advertising. n Price of Anarchy Price of Pure Anarchy >> Price of Stability

Learning Algs + Social Welfare n n n How low can we go? [Kleinberg, P. , Tardos STOC 09] [Roughgarden STOC 09] [Balcan, Blum, Mansour ICS 2010] [Kleinberg, Ligett, P. , Tardos ICS 2011] Cycles of the replicator dynamics in specific games. Price of Anarchy Price of Pure Anarchy >> Price of Stability >> 1 (=OPT)

Learning Algs + Social Welfare n n n How low can we go? [Kleinberg, P. , Tardos STOC 09] [Roughgarden STOC 09] [Balcan, Blum, Mansour ICS 2010] [Kleinberg, Ligett, P. , Tardos ICS 2011] … Price of Anarchy Price of Pure Anarchy >> Price of Stability >> 1 (=OPT)

Thank you