Nmulimea numerelor naturale Zmulimea numerelor ntregi Qmulimea numerelor
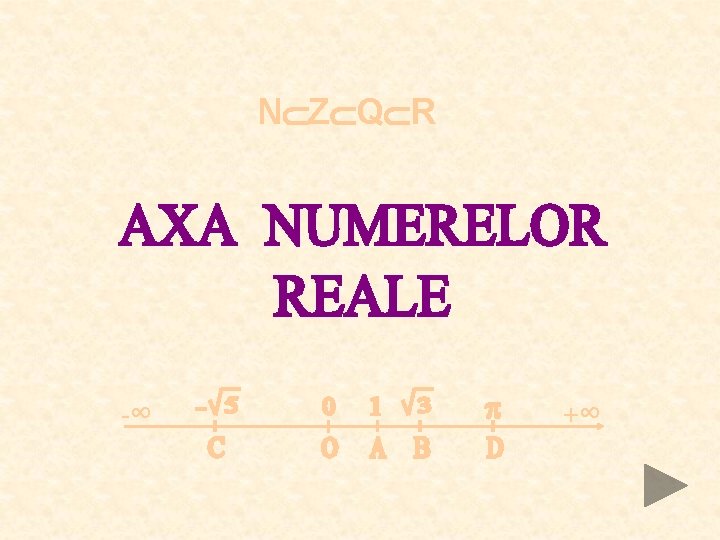



















- Slides: 33
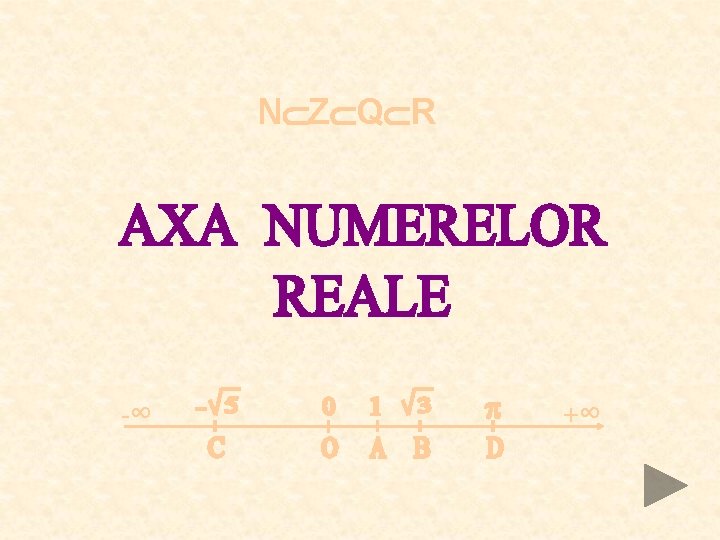

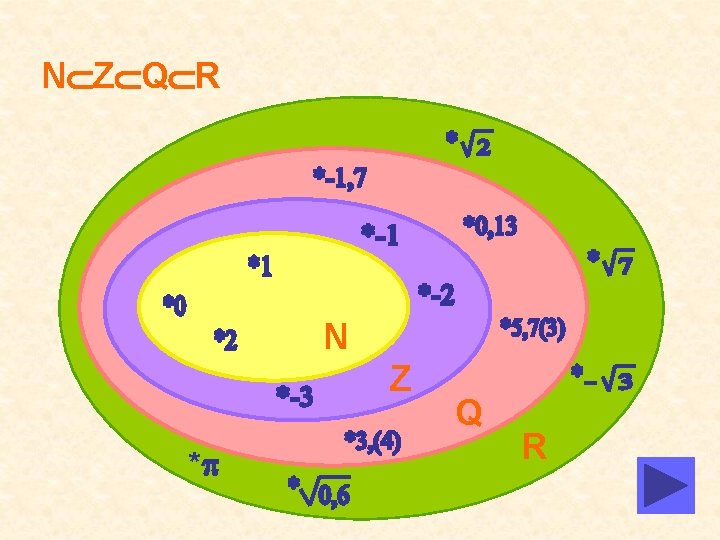
N=mulţimea numerelor naturale Z=mulţimea numerelor întregi Q=mulţimea numerelor raţionale R=mulţimea numerelor reale R-Q=mulţimea numerelor iraţionale

N Z Q R N Z * Q R

Adevărat sau fals ? • Un număr scris cu virgulă nu este întreg. Exemple: 0, 516; -1, 9; +34, 78. • Un număr scris cu liniuţă de fracţie nu este întreg. Exemple: • Un număr scris cu radical nu este raţional. Exemple:

Afirmaţiile anterioare sunt false. Demonstrăm cu metoda contraexemplului. • numere întregi scrise cu virgulă: 51, 0; -852, 0; +6174, 0. • numere întregi scrise cu liniuţă: numere raţionale scrise cu radical: Atenţie ! Nu asociaţi automat numerele scrise cu radical cu numerele iraţionale!

N Z Q R • Georg Cantor (1845 -1918) a avut o contribuţie remarcabilă în fundamentarea teoriei mulţimilor. În acelaşi timp el a dat o construcţie a numerelor reale printr-o metodă diferită de cele realizate de predecesorii săi. • Creator al teoriei numerelor reale, poate fi însă considerat matematicianul grec Eudoxus (408 -355 î. Hr. ) • Ideile sale inspirate din geometrie au fost preluate de Karl Weierstrass (1815 -1897) şi de Richard Dedekind (1831 -1916) şi dezvoltate prin metode aritmetice şi analitice moderne.

Mulţimea numerelor naturale N = { 0, 1, 2, 3, …} • 0 este cel mai mic număr natural. • Nu există cel mai mare număr natural. • Numere care aparţin mulţimii N: 58; 724; 100; 32689; 106. • Numere care nu aparţin mulţimii N: -3; -12; 0, 7; -5, 2(6); ; ; .

Mulţimea numerelor întregi Z = {. . . , -3, -2, -1, 0, 1, 2, 3, …} • Oricărui număr întreg pozitiv îi corespunde un număr întreg negativ. • Numere care aparţin mulţimii Z: 24; -43; 625; -100; 27314; -106. • Numere care nu aparţin mulţimii Z: 8, 1; -0, 5; 9, (7); -1, 3(26); ; ; .

Mulţimea numerelor raţionale • Se notează cu Q • Orice număr raţional se poate scrie sub forma: , a Z, b Z* • Numerele raţionale pot avea după virgulă: - un număr finit de zecimale; - o infinitate de zecimale care se repetă periodic; - o parte finită urmată de o parte periodică. • Numere care aparţin mulţimii Q: 0; 1; 10; -106; 2 -3; -0, 5; 3, (74); 1, 8(2); . • Numere care nu aparţin mulţimii Q: ; ; .

Mulţimea numerelor reale • Se notează cu R • Un număr real este sau raţional, sau iraţional. • Numerele iraţionale au după virgulă o infinitate de zecimale fără parte periodică. • Numere care aparţin mulţimii R: 0; 1; 10; -106; 2 -3 ; -0, 5; 3, (74); 1, 8(2); ; • Numere care nu aparţin mulţimii R: soluţii ale unor ecuaţii precum: x 2+1=0.

Un număr de forma , a N, este iraţional dacă: • Numărul a are ultima cifră 2, 3, 7 sau 8. R-Q pentru că u(152)=2. • Numărul a este cuprius între două pătrate perfecte consecutive. 72<56<82, deci R-Q. • Numărul a admite un divizor p, dar nu admite ca divizor pătratul lui p. R-Q pentru că 115 5 şi 115 25.

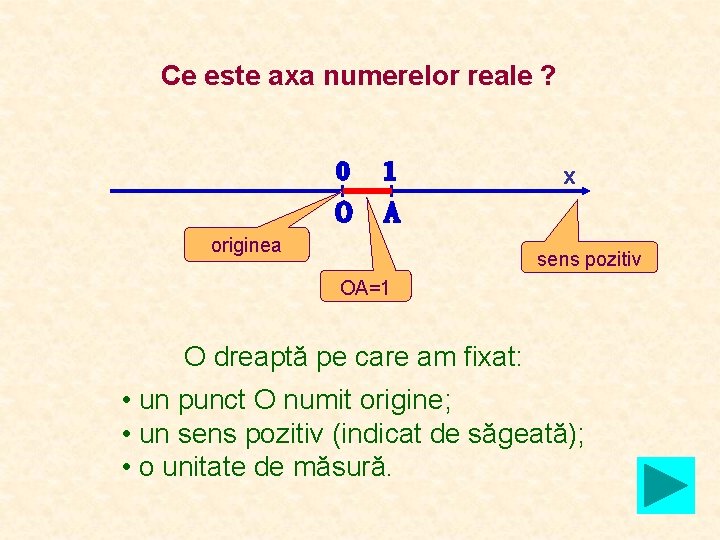
Ce este axa numerelor reale ? x originea sens pozitiv OA=1 O dreaptă pe care am fixat: • un punct O numit origine; • un sens pozitiv (indicat de săgeată); • o unitate de măsură.

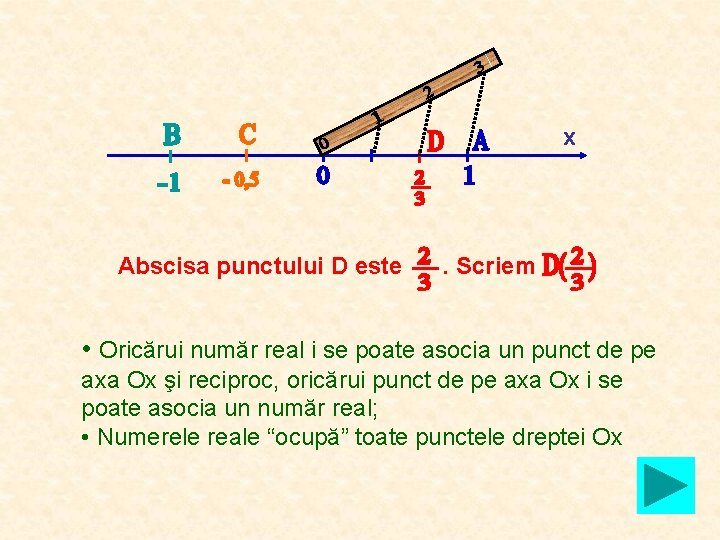
x Abscisa punctului D este . Scriem • Oricărui număr real i se poate asocia un punct de pe axa Ox şi reciproc, oricărui punct de pe axa Ox i se poate asocia un număr real; • Numerele reale “ocupă” toate punctele dreptei Ox

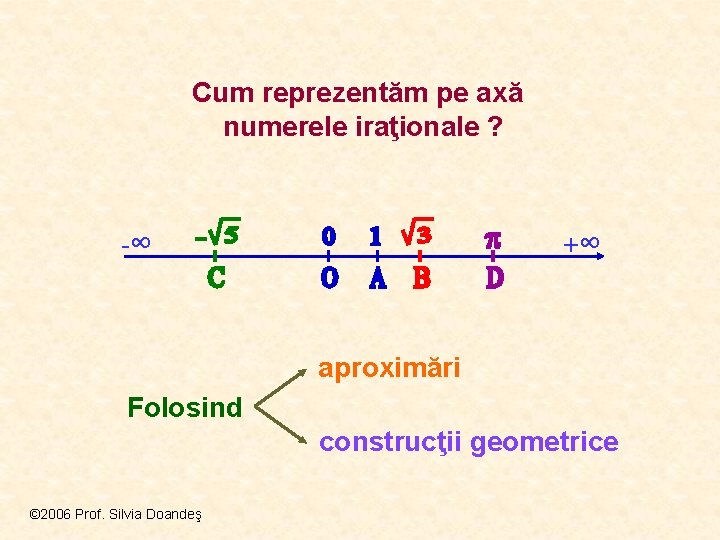
Cum reprezentăm pe axă numerele iraţionale ? -∞ +∞ aproximări Folosind construcţii geometrice © 2006 Prof. Silvia Doandeş

Aproximări În funcţie de precizia cu care dorim să lucrăm, putem înlocui un număr real cu aproximări ale sale, care să aibă un ordin de mărime dat. De cele mai multe ori, nu avem nevoie de o precizie atât de mare încât să folosim rigla şi compasul pentru a reprezenta un număr pe axă. În aceste situaţii, recurgem la încadrarea numărului dat între două numere raţionale care îl aproximează prin lipsă, respectiv prin adaos. Astfel putem reprezenta pe axă numărul dat printr-un punct situat între punctele corespunzătoare unei încadrări date.

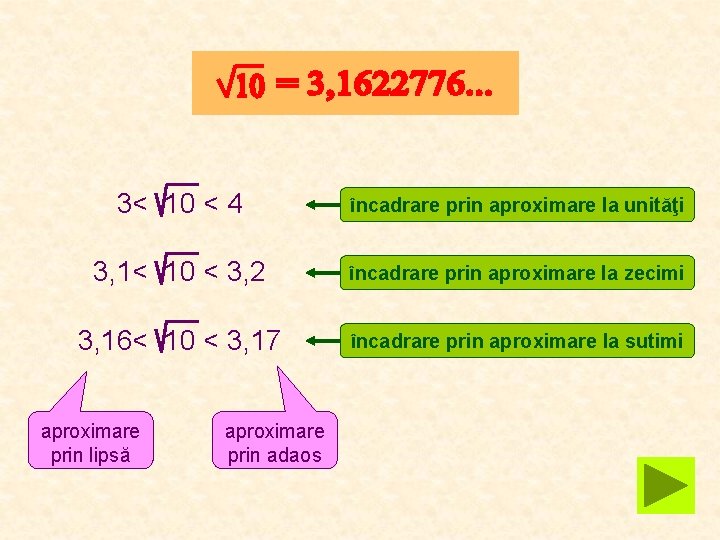
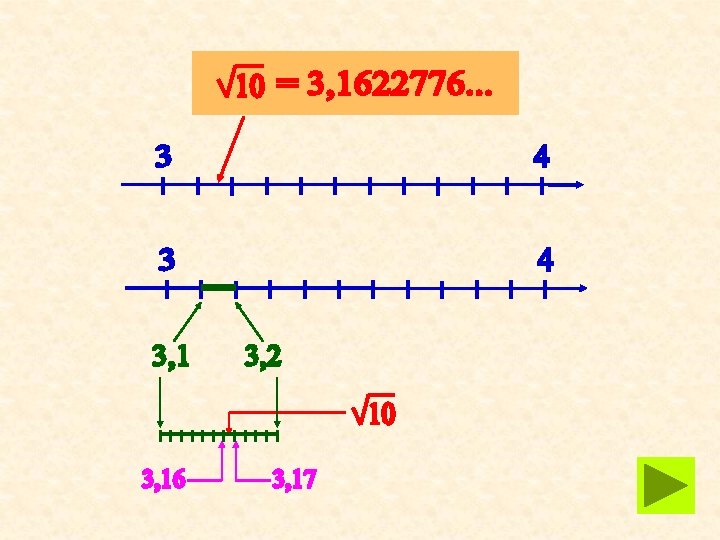
3< 10 < 4 încadrare prin aproximare la unităţi 3, 1< 10 < 3, 2 încadrare prin aproximare la zecimi 3, 16< 10 < 3, 17 încadrare prin aproximare la sutimi aproximare prin lipsă aproximare prin adaos


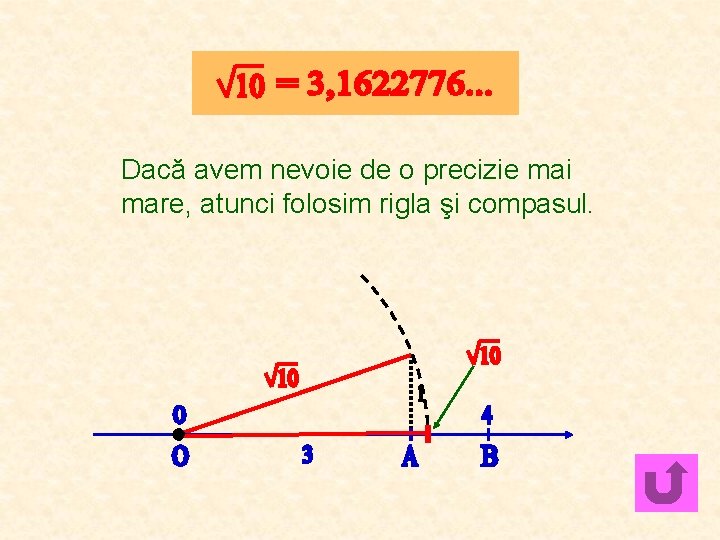
Dacă avem nevoie de o precizie mai mare, atunci folosim rigla şi compasul.

Construcţii geometrice Anumite numere iraţionale, cum sunt radicalii, pot fi reprezentate “exact” pe axa numerelor. Folosim teorema lui Pitagora, rigla şi compasul pentru a construi un segment de lungime : -∞ +∞

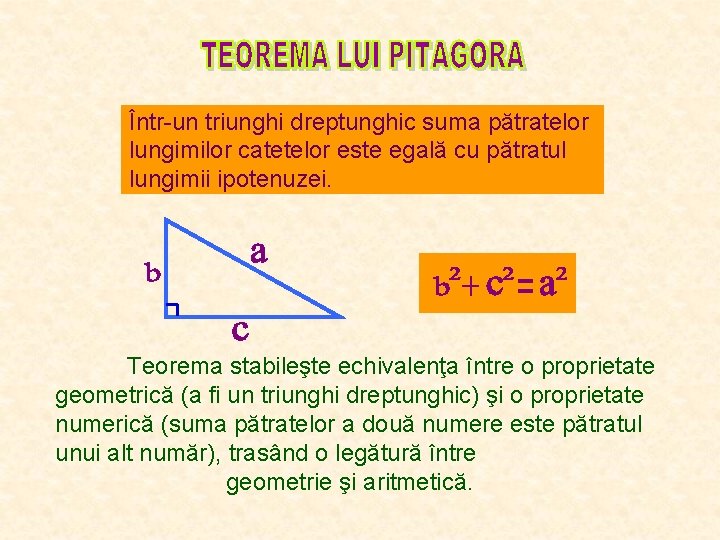
Într-un triunghi dreptunghic suma pătratelor lungimilor catetelor este egală cu pătratul lungimii ipotenuzei. Teorema stabileşte echivalenţa între o proprietate geometrică (a fi un triunghi dreptunghic) şi o proprietate numerică (suma pătratelor a două numere este pătratul unui alt număr), trasând o legătură între geometrie şi aritmetică.

matematician şi filozof grec, spunea: • Cedează întotdeauna cuvintelor blânde şi faptelor folositoare. • Obişnuieşte-te să domini: lăcomia în primul rând, apoi lenea, luxul şi mânia. • Prietenul care ne ascunde defectele, ne slujeşte mai rău decât duşmanul care ni le reproşează. (Vezi I. Dăncilă “Matematica gimnaziului”-pag. 108)

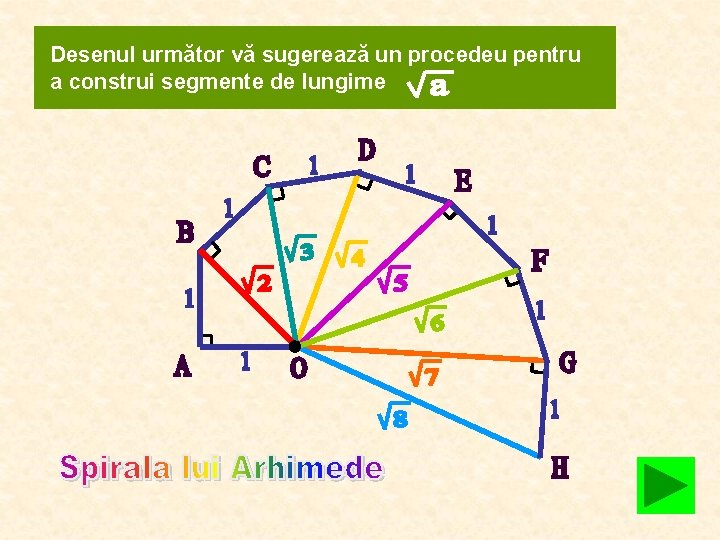
Desenul următor vă sugerează un procedeu pentru a construi segmente de lungime

• a fost nu numai un mare matematician al Siracuzei şi al antichităţii, dar şi unul al tuturor timpurilor. • Pliniu l-a numit “zeul matematicii”, iar Leibniz a scris că, dacă cunoşti opera lui Arhimede, nu mai poţi admira descoperirile noi. • Legendele şi anecdotele care au împodobit invenţiile sale sunt aproape singurele izvoare de unde putem afla amănunte despre opera sa matematică şi inginerească. (Vezi I. Dăncilă “Matematica gimnaziului”-pag. 141)

Folosiţi spirala lui ARHIMEDE pentru a reprezenta pe axa numerelor:

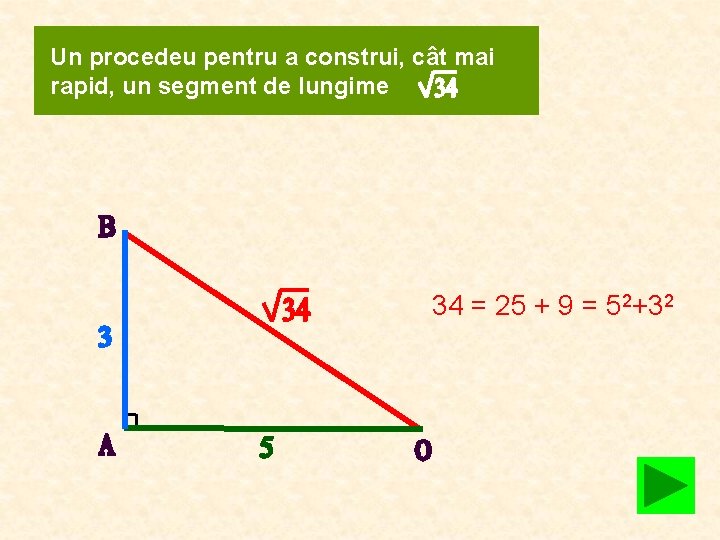
Un procedeu pentru a construi, cât mai rapid, un segment de lungime 34 = 25 + 9 = 52+32

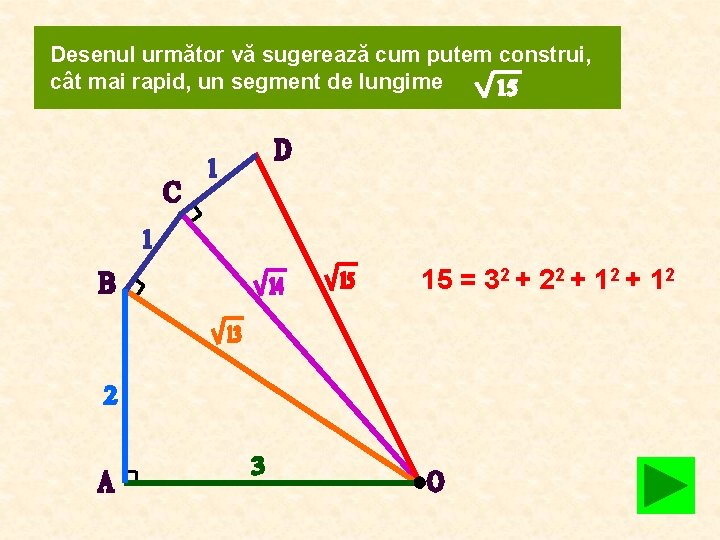
Desenul următor vă sugerează cum putem construi, cât mai rapid, un segment de lungime 15 = 32 + 22 + 12

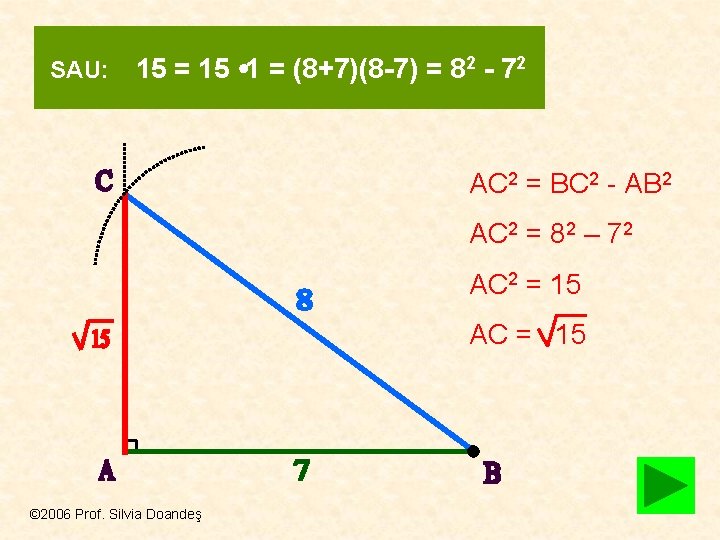
SAU: 15 = 15 1 = (8+7)(8 -7) = 82 - 72 AC 2 = BC 2 - AB 2 AC 2 = 82 – 72 AC 2 = 15 AC = 15 © 2006 Prof. Silvia Doandeş

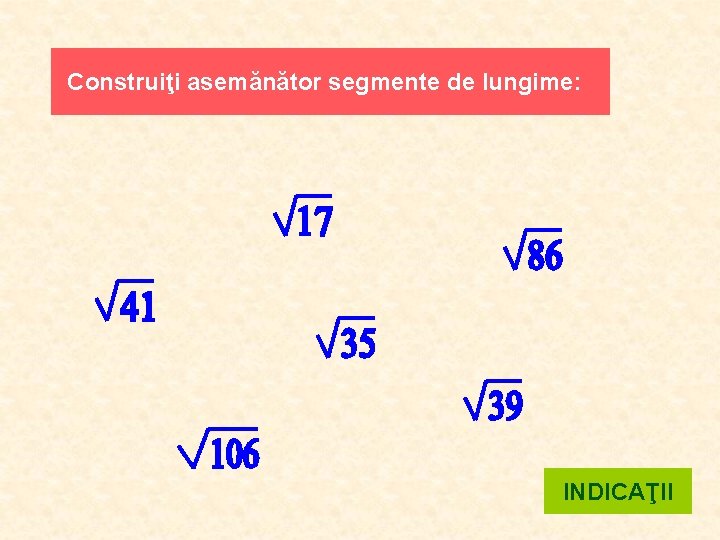
Construiţi asemănător segmente de lungime: INDICAŢII

INDICAŢII 17=16+1 41=25+16 35=25+9+1, sau 35=132 -122 39=36+1+1+1, sau 39=202 -192 86=81+4+1 106=81+25

Numărul 12 345 678 987 654 321 este un număr remarcabil. Dar şi rădăcina lui pătrată este tot aşa: este un număr întreg ! Voi îl puteţi calcula ?

Numărul 12 345 678 987 654 321 • este pătrat perfect şi se citeşte astfel: 12 biliarde, 345 bilioane, 678 miliarde, 987 milioane, 654 mii, 321. • rădăcina lui pătrată este: 111 111.

112=121 1112=12321 11112=1234321 111112=123454321 1111112=12345654321 11111112=1234567654321 11112=123456787654321 111112=12345678987654321

Ai ajuns la sfârşit. ALEGE ! ÎNAPOI IEŞIRE
 Adunarea cu trecere peste ordinul unitatilor si al zecilor
Adunarea cu trecere peste ordinul unitatilor si al zecilor Scrie cu cifre romane următoarele date
Scrie cu cifre romane următoarele date Sisteme de numeratie clasa a v a
Sisteme de numeratie clasa a v a Suma a 6 numere naturale pare distincte este 30
Suma a 6 numere naturale pare distincte este 30 Simetria numerelor
Simetria numerelor Scrieti toate nr naturale care sunt cel mult egale cu 6
Scrieti toate nr naturale care sunt cel mult egale cu 6 Apa element esential al vietii
Apa element esential al vietii Progresie aritmetica formule
Progresie aritmetica formule Hazarde naturale
Hazarde naturale Cos'è un numero naturale
Cos'è un numero naturale La gomma è naturale o artificiale
La gomma è naturale o artificiale Joan naturale
Joan naturale Resursele extraatmosferice
Resursele extraatmosferice Elementele unui lac
Elementele unui lac Sisturi cristaline
Sisturi cristaline Plurale di automa
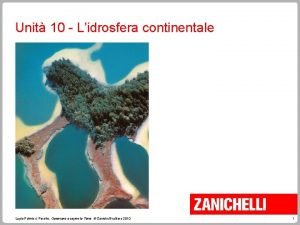
Plurale di automa Idrosfera continentale
Idrosfera continentale Monopolio naturale definizione
Monopolio naturale definizione Indica repetiția din secventa
Indica repetiția din secventa Fibre vegetale naturale
Fibre vegetale naturale Incapacita naturale
Incapacita naturale Autismo naturale mahler
Autismo naturale mahler Satu satu aku sayang ibu
Satu satu aku sayang ibu Test resurse naturale clasa a x-a
Test resurse naturale clasa a x-a Linguaggio naturale matematica
Linguaggio naturale matematica Resursele extraatmosferice si ale atmosferei
Resursele extraatmosferice si ale atmosferei Exemple de ecosisteme
Exemple de ecosisteme Fondo naturale radiazioni
Fondo naturale radiazioni Cele 7 minuni ale lumii naturale
Cele 7 minuni ale lumii naturale Care sunt mijloacele de orientare
Care sunt mijloacele de orientare Obbligazioni naturali
Obbligazioni naturali Metodo celestin freinet
Metodo celestin freinet Inquinamento del mare mappa concettuale
Inquinamento del mare mappa concettuale Lac antropic
Lac antropic