NMR Quantum Information Processing and Entanglement R Laflamme

NMR Quantum Information Processing and Entanglement R. Laflamme, et al. presented by D. Motter

Introduction ► Does NMR entail true quantum computation? ► What about entanglement? ► Also: § What is entanglement (really)? § What is (liquid state) NMR? ► Why are quantum computers more powerful than classical computers

Outline ► Background § States § Entanglement ► Introduction to NMR ► NMR vs. Entanglement ► Conclusions and Discussion

Background: Quantum States ► Pure States § | > = 0|0000> + 1|0001> + … + n|1111> ► Density Operator § Useful for quantum systems whose state is not known ► In most cases we don’t know the exact state § For pure states ► = | >< | § When acted on by unitary U ► U U† § When measured, probability of M = m ► P{ M = m } = tr(Mm†Mm )

Background: Quantum States ► Ensemble of pure states § A quantum system is in one of a number of states | i> ►i is an index ► System in | i> with probability pi § {pi, | i>} is an ensemble ► Density operator § = Σ pi| i>< i| ► If the quantum state is not known exactly § Call it a mixed state

Entanglement ► Seems central to quantum computation ► For pure states: § Entangled if can’t be written as product of states § | > | 1>| 2> | n> ► For mixed states: § Entangled if cannot be written as a convex sum of bi-partite states § Σ ai( 1 2)

Quantum Computation w/o Entanglement ► For pure states: § If there is no entanglement, the system can be simulated classically (efficiently) ►Essentially ► will only have 2 n degrees of freedom For mixed states: § Liquid State NMR at present does not show entanglement § Yet is able to simulate quantum algorithms

Power of Quantum Computing ► Why are Quantum Computers more powerful than their classical counterparts? ► Several alternatives § Hilbert space of size 2 n, so inherently faster ► But we can only measure one such state § Entangled states during computation ► For pure states, this holds. But what about mixed states? ► Some systems with entanglement can be simulated classically § Universe splits Parallel Universes § All a consequence of superpositions

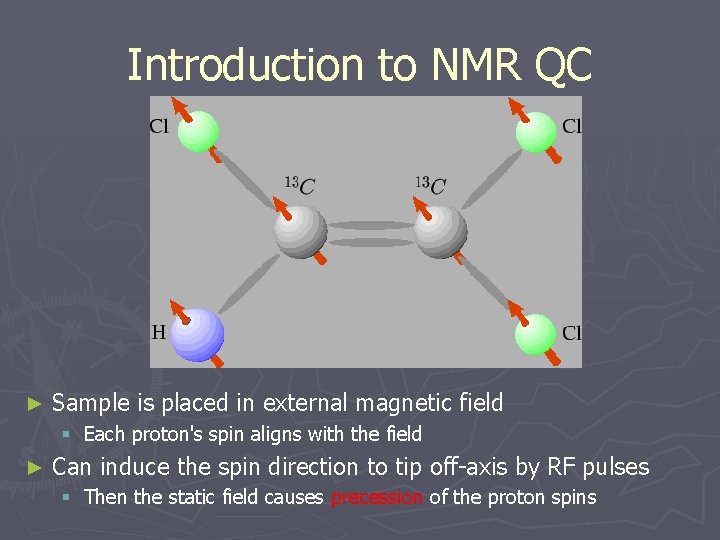
Introduction to NMR QC ► Nuclei possess a magnetic moment § They respond to and can be detected by their magnetic fields ► Single nuclei impossible to detect directly § If many are available they can be observed as an ensemble ► Liquid state NMR Nuclei belong to atoms forming a molecule Many molecules are dissolved in a liquid

Introduction to NMR QC ► Sample is placed in external magnetic field § Each proton's spin aligns with the field ► Can induce the spin direction to tip off-axis by RF pulses § Then the static field causes precession of the proton spins

Difficulties in NMR QC ► Standard QC is based on pure states § In NMR single spins are too weak to measure Must consider ensembles • QC measurements are usually projective • In NMR get the average over all molecules • Suffices for QC • Tendency for spins to align with field is weak • Even at equilibrium, most spins are random • Overcome by method of pseudo-pure states

Entanglement in NMR ► Today’s NMR no entanglement § It is not believed that Liquid State NMR is a promising technology ► Future NMR experiments could show entanglement § Solid state NMR § Larger numbers of qubits in liquid state

Quantifying Entanglement ► Measure entanglement by entropy ► Von Neumann entropy of a state ► If λi are the eigenvalues of ρ, use the equivalent definition:

Quantifying Entanglement ► Basic § properties of Von Neumann’s entropy , equality if and only if in “pure state”. § In a d-dimensional Hilbert space: , the equality if and only if in a completely mixed state, i. e.

Quantifying Entanglement ► Entropy is a measure of entanglement § After partial measurement ►Randomizes the initial state ►Can compute reduced density matrix by partial trace § Entropy of the resulting mixed state measures the amount of this randomization ►The larger the entropy The more randomized the state after measurement The more entangled the initial state was!

Quantifying Entanglement ► Consider a pair of systems (X, Y) ► Mutual Information § I(X, Y) = S(X) + S(Y) – S(X, Y) § J(X, Y) = S(X) – S(X|Y) § Follows from Bayes Rule: ►p(X=x|Y=y) = p(X=x and Y=y)/p(Y=y) ►Then S(X|Y) = S(X, Y) – S(Y) ► For classical systems, we always have I = J

Quantifying Entanglement ► Quantum Systems § S(X), S(Y) come from treating individual subsystems independently § S(X, Y) come from the joint system § S(X|Y) = State of X given Y ► Ambiguous until measurement operators are defined ► Let Pj be a projective measurement giving j with prob pj § S(X|Y) = Σj pj S( X|Pj. Y) ► Define discord (dependent on projectors) § D = J(X, Y) – I(X, Y) ► In NMR, reach states with nonzero discord § Discord central to quantum computation?

Conclusions ► Control over unitary evolution in NMR has allowed small algorithms to be implemented § Some quantum features must be present § Much further than many other QC realizations ► Importance of synthesis realized § Designing a RF pulse sequence which implements an algorithm § Want to minimize imperfections, add error correction

References ► NMR Quantum Information Processing and Entanglement. R. Laflamme and D. Cory. Quantum Information and Computation, Vol 2. No 2. (2002) 166 -176 ► Introduction to NMR Quantum Information Processing. R. Laflamme, et al. April 8, 2002. www. c 3. lanl. gov/~knill/qip/nmrprhtml/ ► Entropy in the Quantum World. Panagiotis Aleiferis, EECS 598 -1 Fall 2001