NMR Pulse NMR pulse length or Tip angle

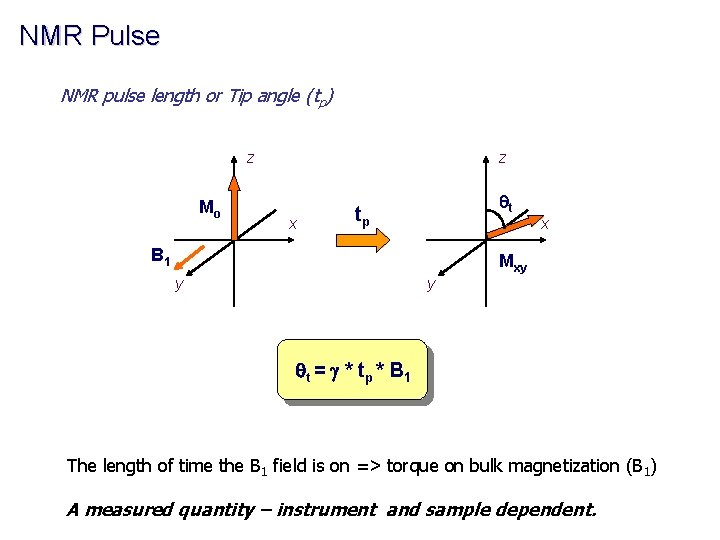
NMR Pulse NMR pulse length or Tip angle (tp) z Mo z x qt tp x B 1 Mxy y y q t = g * tp * B 1 The length of time the B 1 field is on => torque on bulk magnetization (B 1) A measured quantity – instrument and sample dependent.

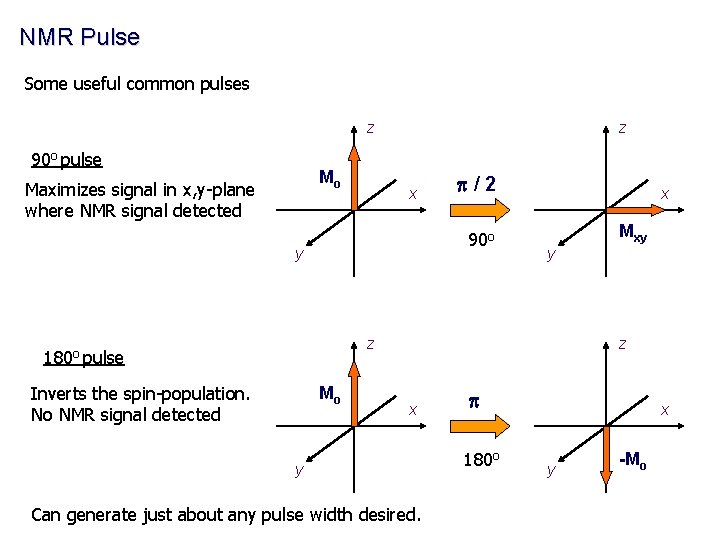
NMR Pulse Some useful common pulses z 90 o pulse Mo Maximizes signal in x, y-plane where NMR signal detected z x p/2 90 o y x Mxy y z 180 o pulse Inverts the spin-population. No NMR signal detected Mo z x y Can generate just about any pulse width desired. p 180 o x y -Mo

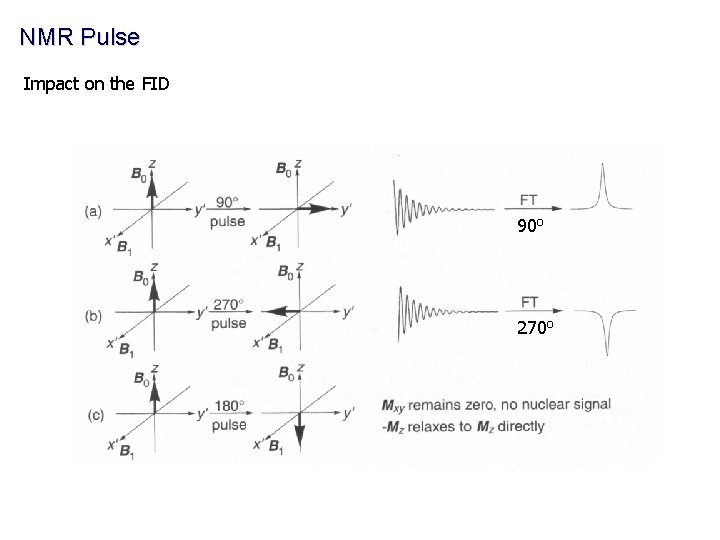
NMR Pulse Impact on the FID 90 o 270 o

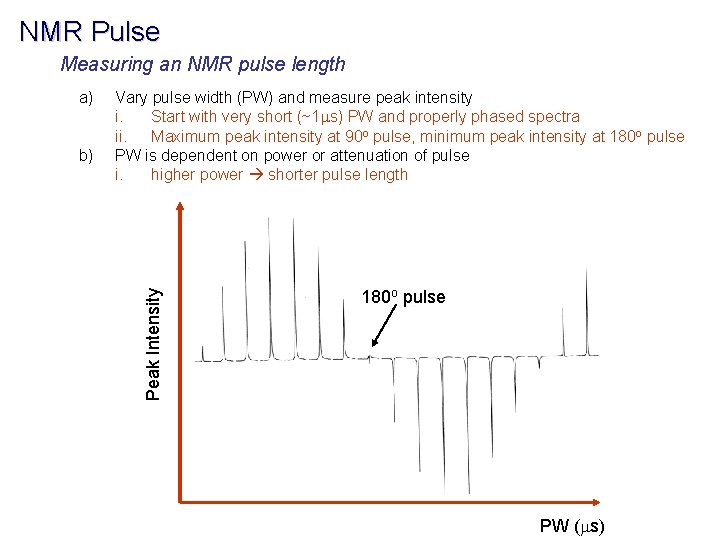
NMR Pulse Measuring an NMR pulse length b) Vary pulse width (PW) and measure peak intensity i. Start with very short (~1 ms) PW and properly phased spectra ii. Maximum peak intensity at 90 o pulse, minimum peak intensity at 180 o pulse PW is dependent on power or attenuation of pulse i. higher power shorter pulse length Peak Intensity a) 180 o pulse PW (ms)

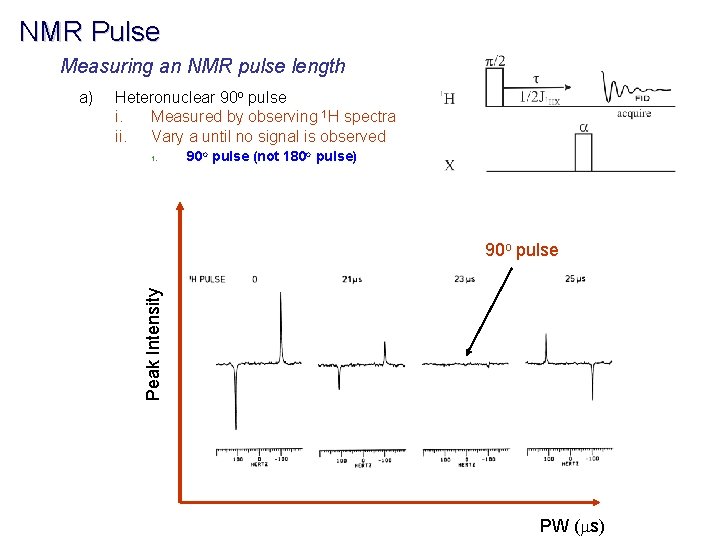
NMR Pulse Measuring an NMR pulse length Heteronuclear 90 o pulse i. Measured by observing 1 H spectra ii. Vary a until no signal is observed 1. 90 o pulse (not 180 o pulse) 90 o pulse Peak Intensity a) PW (ms)

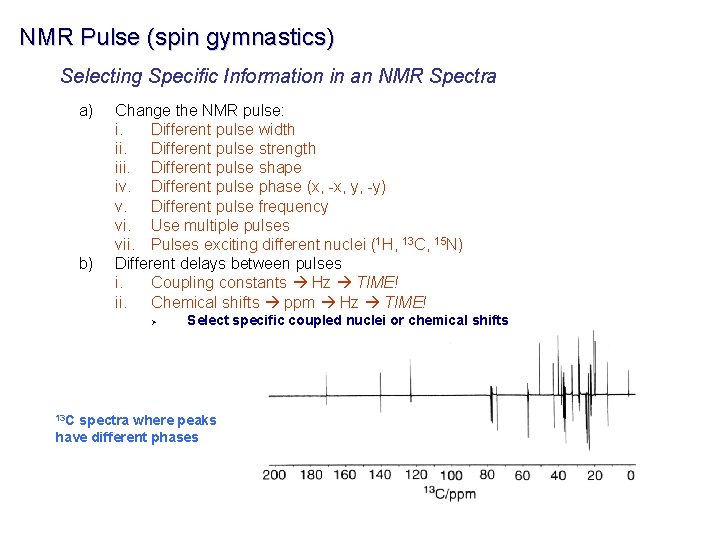
NMR Pulse (spin gymnastics) Selecting Specific Information in an NMR Spectra a) b) Change the NMR pulse: i. Different pulse width ii. Different pulse strength iii. Different pulse shape iv. Different pulse phase (x, -x, y, -y) v. Different pulse frequency vi. Use multiple pulses vii. Pulses exciting different nuclei (1 H, 13 C, 15 N) Different delays between pulses i. Coupling constants Hz TIME! ii. Chemical shifts ppm Hz TIME! Ø 13 C Select specific coupled nuclei or chemical shifts spectra where peaks have different phases

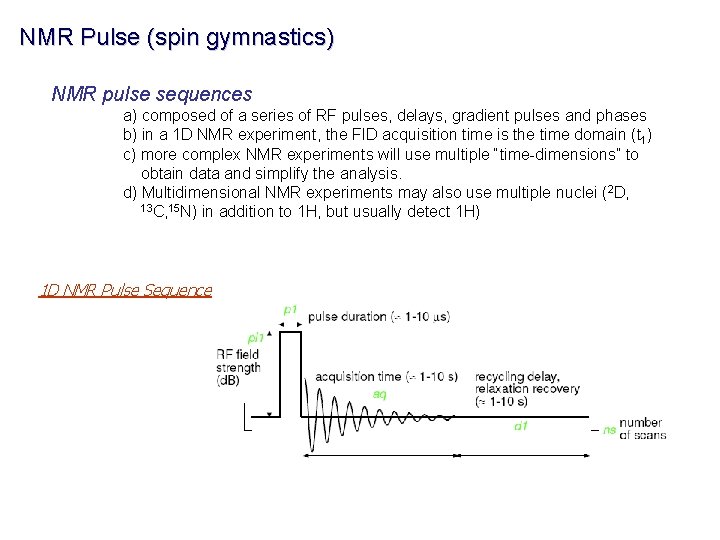
NMR Pulse (spin gymnastics) NMR pulse sequences a) composed of a series of RF pulses, delays, gradient pulses and phases b) in a 1 D NMR experiment, the FID acquisition time is the time domain (t 1) c) more complex NMR experiments will use multiple “time-dimensions” to obtain data and simplify the analysis. d) Multidimensional NMR experiments may also use multiple nuclei (2 D, 13 C, 15 N) in addition to 1 H, but usually detect 1 H) 1 D NMR Pulse Sequence

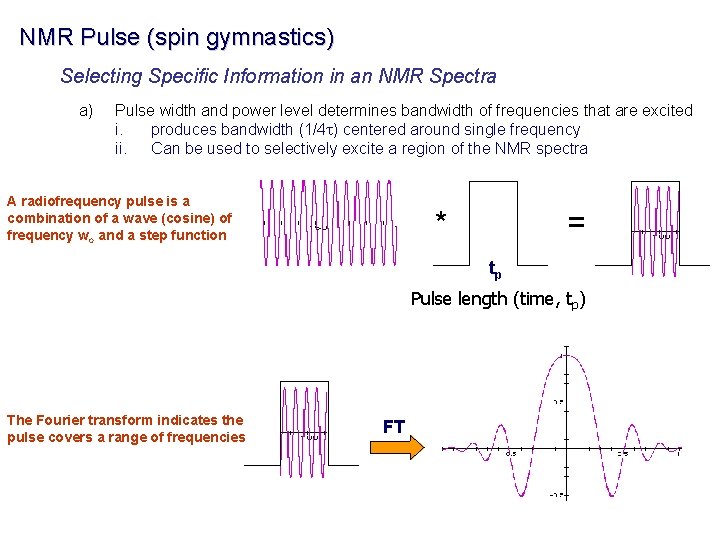
NMR Pulse (spin gymnastics) Selecting Specific Information in an NMR Spectra a) Pulse width and power level determines bandwidth of frequencies that are excited i. produces bandwidth (1/4 t) centered around single frequency ii. Can be used to selectively excite a region of the NMR spectra A radiofrequency pulse is a combination of a wave (cosine) of frequency wo and a step function * = tp Pulse length (time, tp) The Fourier transform indicates the pulse covers a range of frequencies FT

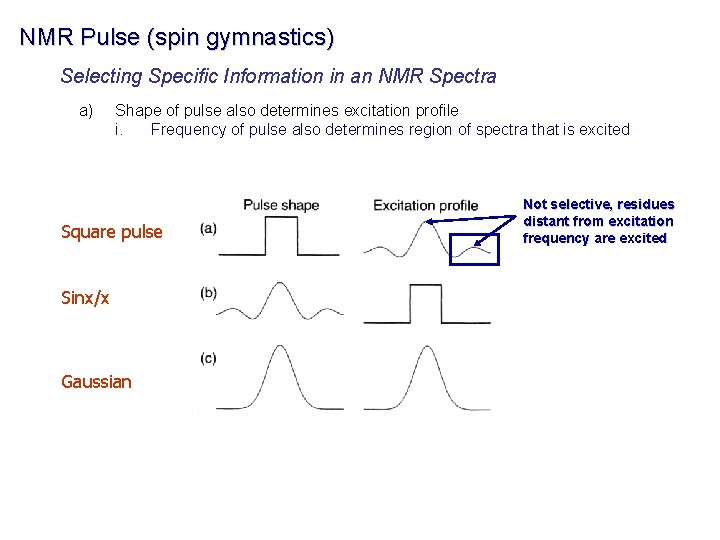
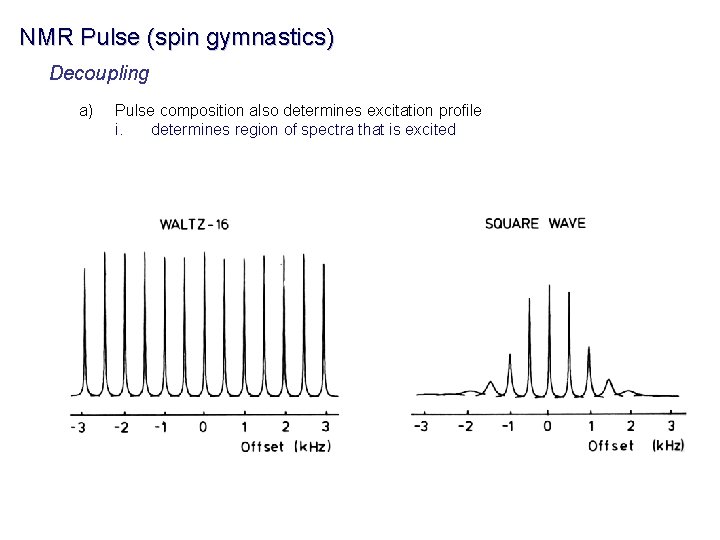
NMR Pulse (spin gymnastics) Selecting Specific Information in an NMR Spectra a) Shape of pulse also determines excitation profile i. Frequency of pulse also determines region of spectra that is excited Square pulse Sinx/x Gaussian Not selective, residues distant from excitation frequency are excited

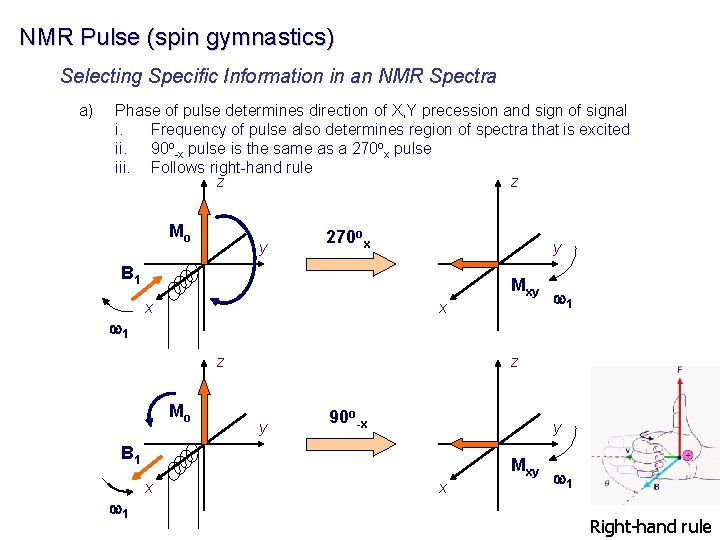
NMR Pulse (spin gymnastics) Selecting Specific Information in an NMR Spectra a) Phase of pulse determines direction of X, Y precession and sign of signal i. Frequency of pulse also determines region of spectra that is excited ii. 90 o-x pulse is the same as a 270 ox pulse iii. Follows right-hand rule z z Mo y 270 ox y B 1 w 1 Mxy x x z Mo z y 90 o-x y B 1 w 1 Mxy x w 1 Right-hand rule

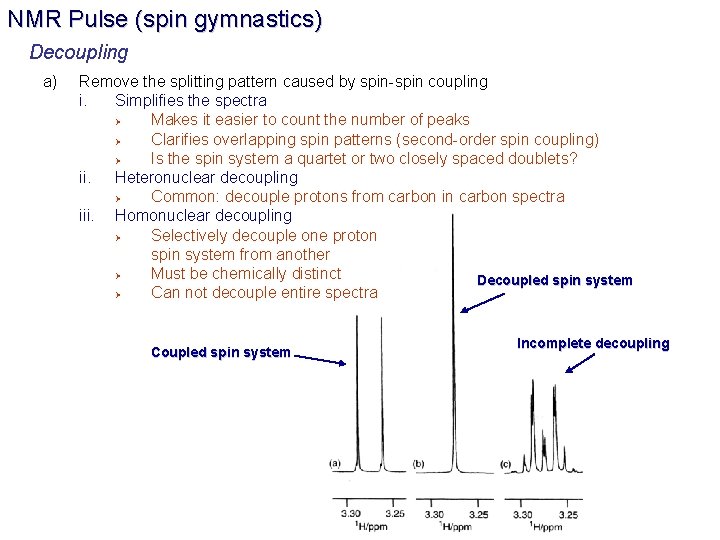
NMR Pulse (spin gymnastics) Decoupling a) Remove the splitting pattern caused by spin-spin coupling i. Simplifies the spectra Ø Makes it easier to count the number of peaks Ø Clarifies overlapping spin patterns (second-order spin coupling) Ø Is the spin system a quartet or two closely spaced doublets? ii. Heteronuclear decoupling Ø Common: decouple protons from carbon in carbon spectra iii. Homonuclear decoupling Ø Selectively decouple one proton spin system from another Ø Must be chemically distinct Decoupled spin system Ø Can not decouple entire spectra Coupled spin system Incomplete decoupling

NMR Pulse (spin gymnastics) Decoupling a) Heteronuclear i. Apply a second strong radiofrequency field (B 2) Ø For a decoupled 13 C spectra, pulse is at 1 H frequency 1 H nuclei continually precess about B M averages to zero! 2 z Ø If MZ =0, coupling vanishes and 13 C resonances reduce to singlet Ø Decoupling requires the magnitude of B 2 be much greater than the 1 H-13 C coupling constant ( ~140 Hz) 13 C 1 H pulses

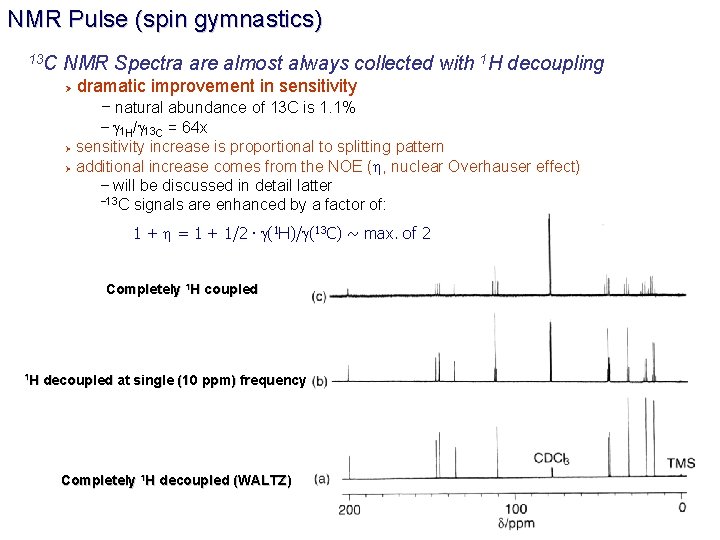
NMR Pulse (spin gymnastics) 13 C NMR Spectra are almost always collected with 1 H decoupling Ø dramatic improvement in sensitivity – natural abundance of 13 C is 1. 1% – g 1 H/g 13 C = 64 x Ø sensitivity increase is proportional to splitting pattern Ø additional increase comes from the NOE (h, nuclear Overhauser effect) – will be discussed in detail latter – 13 C signals are enhanced by a factor of: 1 + h = 1 + 1/2. g(1 H)/g(13 C) ~ max. of 2 Completely 1 H coupled 1 H decoupled at single (10 ppm) frequency Completely 1 H decoupled (WALTZ)

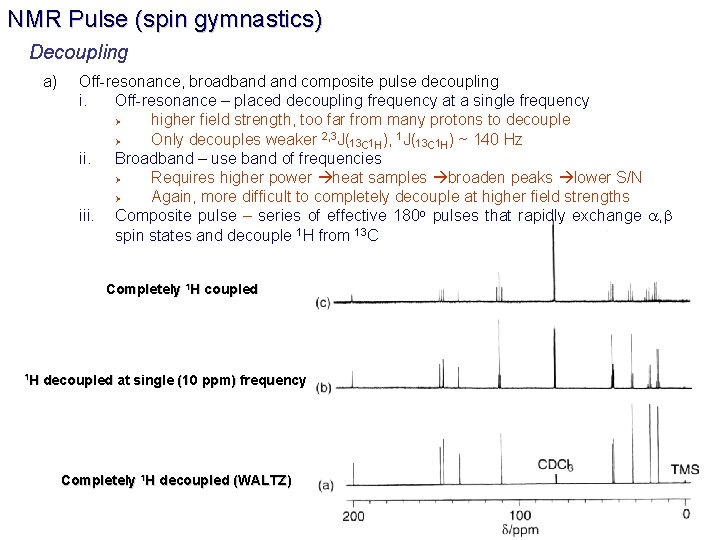
NMR Pulse (spin gymnastics) Decoupling a) Off-resonance, broadband composite pulse decoupling i. Off-resonance – placed decoupling frequency at a single frequency Ø higher field strength, too far from many protons to decouple Ø Only decouples weaker 2, 3 J(13 C 1 H), 1 J(13 C 1 H) ~ 140 Hz ii. Broadband – use band of frequencies Ø Requires higher power heat samples broaden peaks lower S/N Ø Again, more difficult to completely decouple at higher field strengths iii. Composite pulse – series of effective 180 o pulses that rapidly exchange a, b spin states and decouple 1 H from 13 C Completely 1 H coupled 1 H decoupled at single (10 ppm) frequency Completely 1 H decoupled (WALTZ)

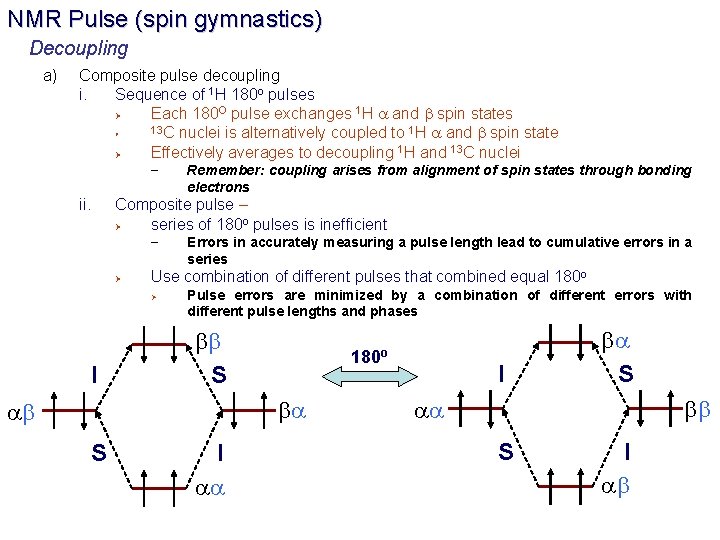
NMR Pulse (spin gymnastics) Decoupling a) Composite pulse decoupling i. Sequence of 1 H 180 o pulses Ø Each 180 O pulse exchanges 1 H a and b spin states 13 C nuclei is alternatively coupled to 1 H a and b spin state Ø Effectively averages to decoupling 1 H and 13 C nuclei Ø – ii. Remember: coupling arises from alignment of spin states through bonding electrons Composite pulse – Ø series of 180 o pulses is inefficient – Ø Use combination of different pulses that combined equal 180 o Ø I Errors in accurately measuring a pulse length lead to cumulative errors in a series Pulse errors are minimized by a combination of different errors with different pulse lengths and phases bb S 180 o ba ab S I aa I ba S bb aa S I ab

NMR Pulse (spin gymnastics) Decoupling a) Composite pulse decoupling i. Sequence of 1 H 180 o pulses Ø Each spin precess in the X, Y plane at a rate equal to the sum of its chemical shift and ½ its coupling constants Ø Each 180 O pulse inverts the evolution of the two spins in the X, Y plane Ø Result is the two spins for the coupled doublet precess as the same rate of a decoupled singlet – Effectively removes the coupling constant contribution to its rate of precessing in the X, Y plane The relative evolution in the X, Y plane for the separation of the coupled doublets relative to the decoupled singlet. The 180 o pulse flip the direction of the evolution of the two components of the doublet in the X, Y plane such that the effective motion resembles the decoupled singlet

NMR Pulse (spin gymnastics) Decoupling a) MLEV-4 composite pulse decoupling scheme i. Based on the composite pulse: Ø (90 o)x(270 o)y(90 o)x = R MLEV-16 decouples efficiently ± 4. 5 k. Hz b) WALTZ-16 i. Based on the composite pulse: Ø (90 o)x(180 o)-x(270 o)x decouples efficiently over ± 6 k. Hz Ø Corrects imperfections in MLEV Ø 90 o ~ 100 ms reduces sample heating Ø 1 = 90 o, 2=180 o, 3=270 o, 4=360 o c) GARP i. Computer optimized using non-90 o flip angles Ø Effective decoupling bandwidth of ± 15 k. Hz Ø 90 o ~ 70 ms Trajectory of 1 H nuclei after two R MLEV-4 pulses results in an effective 360 O pulse. Results is improved slightly by following with two R pulses with reverse phase. NMR IN BIOMEDICINE, VOL. 10, 372– 380 (1997)

NMR Pulse (spin gymnastics) Decoupling a) Pulse composition also determines excitation profile i. determines region of spectra that is excited

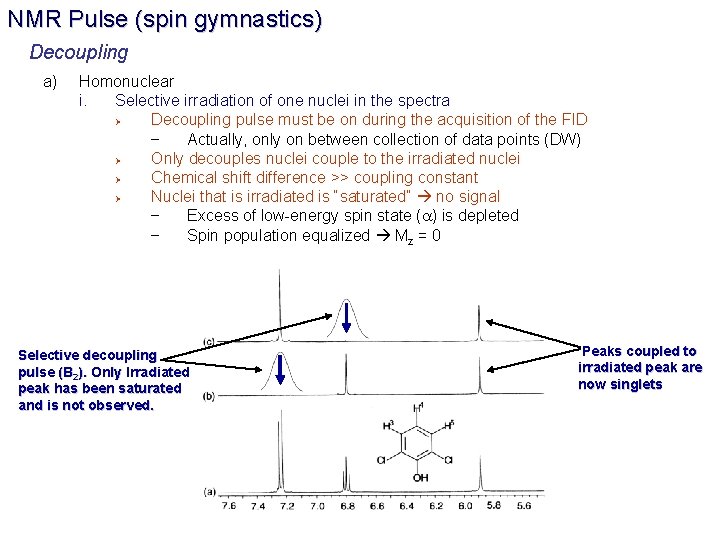
NMR Pulse (spin gymnastics) Decoupling a) Homonuclear i. Selective irradiation of one nuclei in the spectra Ø Decoupling pulse must be on during the acquisition of the FID – Actually, only on between collection of data points (DW) Ø Only decouples nuclei couple to the irradiated nuclei Ø Chemical shift difference >> coupling constant Ø Nuclei that is irradiated is “saturated” no signal – Excess of low-energy spin state (a) is depleted – Spin population equalized Mz = 0 Selective decoupling pulse (B 2). Only Irradiated peak has been saturated and is not observed. Peaks coupled to irradiated peak are now singlets

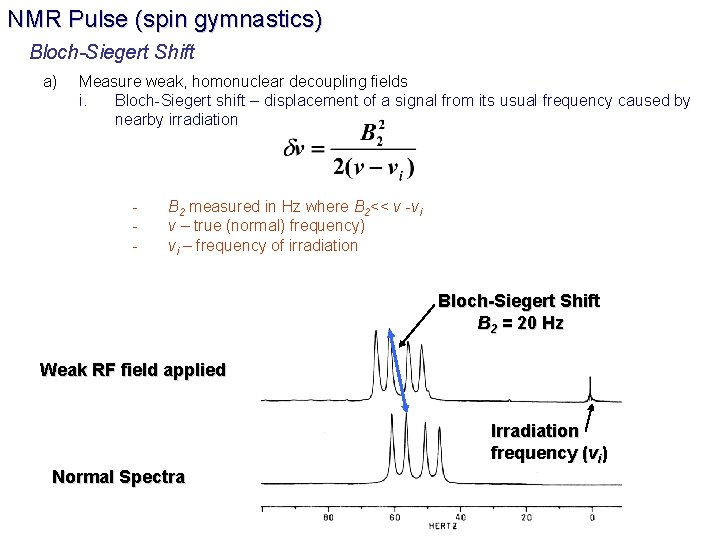
NMR Pulse (spin gymnastics) Bloch-Siegert Shift a) Measure weak, homonuclear decoupling fields i. Bloch-Siegert shift – displacement of a signal from its usual frequency caused by nearby irradiation - B 2 measured in Hz where B 2<< v -vi v – true (normal) frequency) vi – frequency of irradiation Bloch-Siegert Shift B 2 = 20 Hz Weak RF field applied Irradiation frequency (vi) Normal Spectra

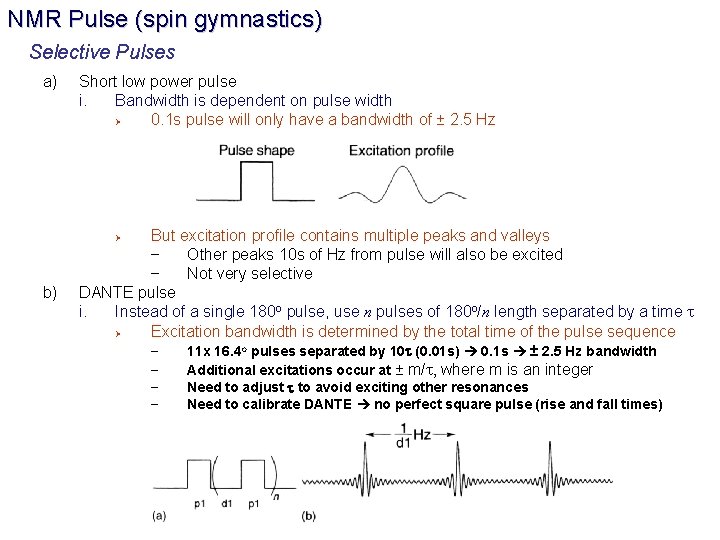
NMR Pulse (spin gymnastics) Selective Pulses a) Short low power pulse i. Bandwidth is dependent on pulse width Ø 0. 1 s pulse will only have a bandwidth of ± 2. 5 Hz But excitation profile contains multiple peaks and valleys – Other peaks 10 s of Hz from pulse will also be excited – Not very selective DANTE pulse i. Instead of a single 180 o pulse, use n pulses of 180 o/n length separated by a time t Ø Excitation bandwidth is determined by the total time of the pulse sequence Ø b) – – 11 x 16. 4 o pulses separated by 10 t (0. 01 s) 0. 1 s ± 2. 5 Hz bandwidth Additional excitations occur at ± m/t, where m is an integer Need to adjust t to avoid exciting other resonances Need to calibrate DANTE no perfect square pulse (rise and fall times)

NMR Pulse (spin gymnastics) Composite Pulses a) Composite 180 o pulse i. (90 o)x(180 o)y(90 o)x ii. Difficult to accurately determine a 90 o or 180 o pulse Ø Effect of pulse may vary over the coils in the probe, especially at edges Ø Depends on the exact tuning of the probe iii. Results in loss of S/N and creates artifacts iv. 20 ms 180 o pulse ± 12. 5 k. Hz excitation bandwidth (± 1/4 x. PW) Ø Problem when spectral width is larger than excitation bandwidth v. Composite pulses have larger excitation bandwidths Trajectory of (90 o)x(180 o)y(90 o)x composite pulse with an incorrect 180 o pulse length, where the effective pulse is 160 o. Even with the significant error, the net magnetization still winds up very close to -z

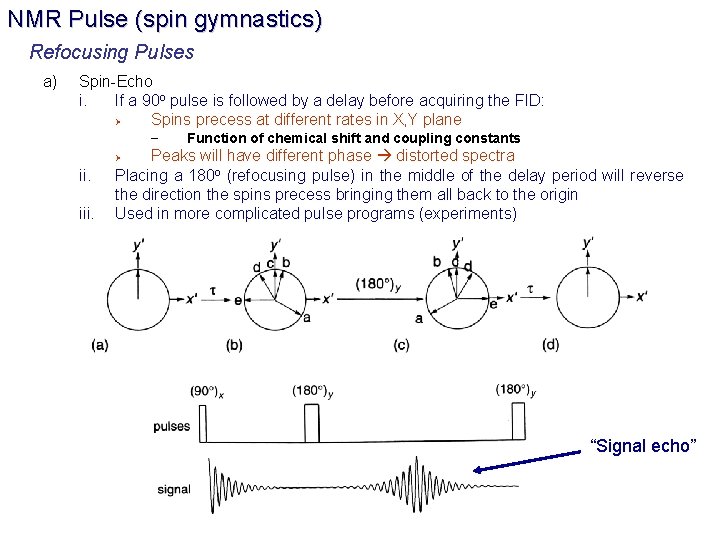
NMR Pulse (spin gymnastics) Refocusing Pulses a) Spin-Echo i. If a 90 o pulse is followed by a delay before acquiring the FID: Ø Spins precess at different rates in X, Y plane – Function of chemical shift and coupling constants Peaks will have different phase distorted spectra Placing a 180 o (refocusing pulse) in the middle of the delay period will reverse the direction the spins precess bringing them all back to the origin Used in more complicated pulse programs (experiments) Ø ii. iii. “Signal echo”

NMR Pulse (spin gymnastics) Spin-Lock Pulse Sequence a) Modified Spin-Echo Pulse i. Make t very short and repeat 180 o pulse n times (90 o)x – {(180 o)y}n n is a very large number B 1 field is continuous and magnetization is now locked in the y’ direction Effective magnetic field is now B 1 (not Bo) 1. nuclei precess around B 1 2. nuclei tumble rapidly relative to B 1 Ø ii. iii.

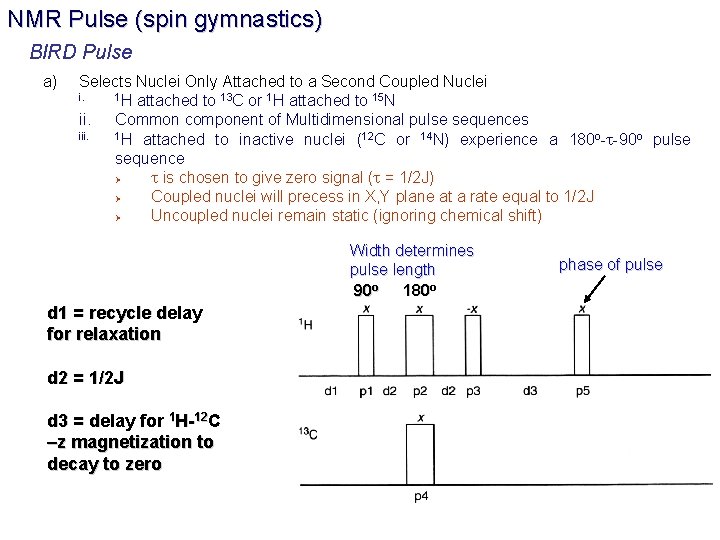
NMR Pulse (spin gymnastics) BIRD Pulse a) Selects Nuclei Only Attached to a Second Coupled Nuclei i. 1 H attached to 13 C or 1 H attached to 15 N ii. Common component of Multidimensional pulse sequences iii. 1 H attached to inactive nuclei (12 C or 14 N) experience a 180 o-t-90 o pulse sequence Ø t is chosen to give zero signal (t = 1/2 J) Ø Coupled nuclei will precess in X, Y plane at a rate equal to 1/2 J Ø Uncoupled nuclei remain static (ignoring chemical shift) Width determines pulse length 180 o 90 o d 1 = recycle delay for relaxation d 2 = 1/2 J d 3 = delay for 1 H-12 C –z magnetization to decay to zero phase of pulse

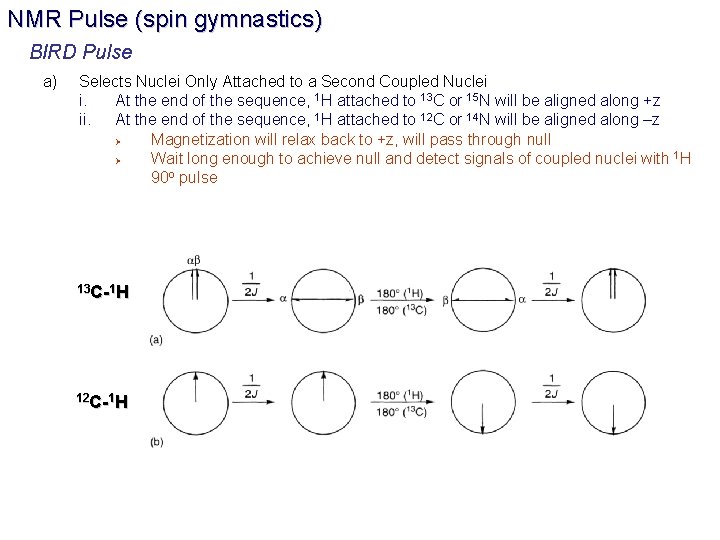
NMR Pulse (spin gymnastics) BIRD Pulse a) Selects Nuclei Only Attached to a Second Coupled Nuclei i. At the end of the sequence, 1 H attached to 13 C or 15 N will be aligned along +z ii. At the end of the sequence, 1 H attached to 12 C or 14 N will be aligned along –z Ø Magnetization will relax back to +z, will pass through null Ø Wait long enough to achieve null and detect signals of coupled nuclei with 1 H 90 o pulse 13 C-1 H 12 C-1 H