Nmeros complejos lgebra Superior Definicin Los nmeros complejos

Números complejos Álgebra Superior

Definición Los números complejos aparecen como solución de algunas ecuaciones cuadráticas. En general, cualquier ecuación de grado mayor que 1 puede tener como solución un número complejo. Los números complejos están relacionados con la extracción de raíces pares de números negativos. Definiremos un número complejo como un par ordenado de números reales (a; b) Ejemplos: (3; 5) (-1. 922; 0. 003) (17. 28892; -5. 8276)

Igualdad Dos números complejos (a; b) y (c; d) son iguales si y solo si a = c y b = d. De acuerdo con esto: (2; √ 12) = ( ½ √ 7 + 4√ 3) + ½ √ 7 – 4√ 3 ); 2 √ 3) Ya que 2 = ½ √ 7 + 4√ 3 + ½ √ 7 – 4√ 3 √ 12 = 2 √ 3 Por el contrario (– 1; 1) (1; – 1) ?

Suma y producto Definimos la suma de complejos como: (a; b) + (c; d) = (a + c; b + d) Ejemplos: (2; – 4) + (5; 6) = (7; 2) (– 3; 8) + (– 1; – 4) = (– 4; 4) Definimos la multiplicación de complejos como: (a; b) · (c; d) = (ac – bd; ad + bc) Ejemplos: (2; – 4) · (5; 6) = (2· 5–(– 4)· 6; 2· 6+5(– 4)) = (10+24; 12– 20) = (34; – 8)) (– 3; 8) · (– 1; – 4) = ((– 3)(– 1) – 8(– 4); (– 3)(– 4)+8(– 1)) = (3+32; 12 – 8 ) = (35; 4)

Propiedades de la suma y la multiplicación Las propiedades fundamentales de los reales se extienden fácilmente a los números complejos. 1. Conmutatividad para la suma: (a; b) + (c; d) = (c; d) +(a; b) 2. Asociatividad para la suma: ((a; b) + (c; d)) + (e; f) = (a; b) + ((c; d) + (e; f)) 3. Conmutatividad para la multiplicación: (a; b) · (c; d) = (c; d) · (a; b)

Propiedades de la suma y la multiplicación (cont. ) 4. Asociatividad para la multiplicación: ((a; b) · (c; d)) · (e; f) = (a; b) · ((c; d) · (e; f)) 5. Distributividad: (a; b) · ((c; d)+ (e; f) )= (a; b) · (c; d) + (a; b) · (e; f)

Sustracción La resta de un complejo (c; d) de otro (a; b) es un complejo (x; y) tal que (c; d) + (x; y) = (a; b) Esto implica que c+x=a y d+y=b y y=b–d De aquí que x=a–c Por lo tanto (a; b) – (c; d) = (a – c; b – d)

Propiedades de la sustracción Se cumple lo siguiente: (a; b) – (a; b) = (0; 0) (a; b) + (0; 0) = (a; b) Ejemplos: (3; – 5) – (8; 3) = (– 5; – 8) (10; 14) – (7; 10) = (3; 4)

División La división de un complejo (a; b) entre otro (c; d) es un complejo (x; y) tal que (c; d) · (x; y) = (a; b) Esto implica que c x – dy = a (1) y dx + cy = b (2) De (1), x = (a + dy)/c, sustituyendo en (2) d(a+ dy)/c +cy = b. d 2 y + c 2 y = bc – ad. Por lo tanto y = (bc – ad )/(d 2 + c 2) y x = (a + d (bc – ad )/(d 2 + c 2))/c = (ad 2+ac 2+dbc-ad 2)/((d 2 + c 2)c) = (ac+db)/(d 2 + c 2) (a; b) / (c; d) = ((ac+db)/(d 2 + c 2); (bc – ad )/(d 2 + c 2))

Forma binómica Todo número complejo se puede escribir en la forma (a; b) = a + bi Donde i representa (0; 1) y a y b son números complejos (a; 0) y (0; b). Aplicando la regla de la multiplicación (0; 1)2 = (– 1; 0) Así que i 2 = – 1

Ejemplos (1 + i)3 = (1 + i)(1 + 2 i + i 2) = (1 + i)(1 + 2 i – 1) = (1 + i)2 i = 2 i + 2 i 2= – 2+2 i (3 – 6 i)(6 – i) = 18 – 3 i – 36 i + 6 i 2 = 18 – 39 i – 6 = 12 – 39 i En el caso de la división multiplicamos numerador y denominador por el denominador con el factor de i cambiado de signo. (4 + 5 i) / (2 – 3 i) = ((4 + 5 i) (2 + 3 i) ) /((2 – 3 i) (2 + 3 i) ) = (8 + 12 i + 10 i + 15 i 2)/(4 – 9 i 2) = (– 7 +22 i)/(13) = – 7/13 + 22 i/13

Parte real e imaginaria Un número complejo a + bi se compone de dos partes, la parte real a y la imaginaria b. Ambas partes son números reales. Se denota la parte real por: a = R(a + bi) Y la imaginaria por b = I(a + bi) Dos números complejos a + bi y a – bi se llaman complejos conjugados. El complejo conjugado de un número se designa por A 0 o A.

El producto AA 0 = (a + bi) (a – bi) = a 2 + b 2 Es un número real y se le conoce como norma de A. La raíz cuadrada de la norma de A es el valor absoluto o módulo de A y se designa por | A | o mod(A). | a + bi | = √(a 2 + b 2) O mod(a + bi) = √(a 2 + b 2)

Propiedades del conjugado Se cumplen las siguientes proposiciones: Si C = A + B, entonces C 0 = A 0 + B 0 Si C = AB, entonces C 0 = A 0 B 0 Si C = A – B, entonces C 0 = A 0 – B 0 Si C = A/B, entonces C 0 = A 0/B 0

Propiedades del módulo Teorema. El módulo de un producto es igual al producto de los módulos de sus factores. | ABC…L | = | A||B||C|…|L | Demostración. Sea X = AB, XX 0 = (AB)0 = (AB) (A 0 B 0) = (AA 0) (BB 0) Sacando raíz cuadrada √(XX 0) = | X | = √(AA 0) √(BB 0) = |A||B| Es fácil generalizar para n factores.

Ejercicios Encontrar el módulo

Desigualdad del módulo de la suma Teorema. El módulo de una suma es menor o igual a la suma de los módulos de sus sumandos. | A+B+C+…+L | | A|+|B|+|C|+…+|L | Siendo iguales cuando todos los cocientes B/A, C/A, …, L/A Sean reales no negativos ejemplo. | (5 – 3 i) + (8 – 7 i) + (2 + i)| = | 15 – 9 i | = √(152 + 92) = 17. 49 | (5 – 3 i)|+|(8 – 7 i)| +|(2 + i)| = √(52+32)+√(82+72)+√(22+12) = = √ 34+ √ 113+√ 5 = 5. 83+10. 63+2. 24= 18. 7

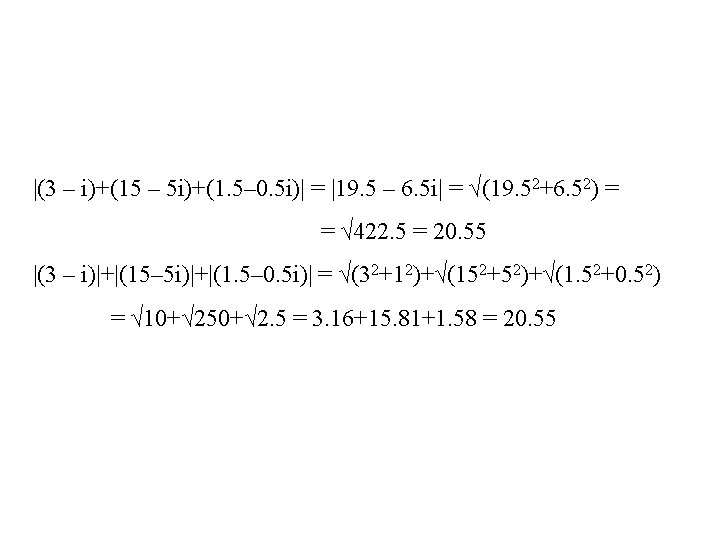
|(3 – i)+(15 – 5 i)+(1. 5– 0. 5 i)| = |19. 5 – 6. 5 i| = √(19. 52+6. 52) = = √ 422. 5 = 20. 55 |(3 – i)|+|(15– 5 i)|+|(1. 5– 0. 5 i)| = √(32+12)+√(152+52)+√(1. 52+0. 52) = √ 10+√ 250+√ 2. 5 = 3. 16+15. 81+1. 58 = 20. 55

Raíz cuadrada de un complejo Sea X 2 = A con X = x + iy, A = a + bi. Entonces (x + iy)2 = a + bi x 2 + 2 ixy – y 2 = a + bi pero (x 2 + y 2)2 = (x 2 – y 2)2 + 4 x 2 y 2 Junto con (1) nos da 2 xy = b (1) { x 2 – y 2 = a, { O b 2 a 2 √(x 2 + y 2)2 = x 2 + y 2 = √( a 2 +b 2) De (1) y 2 = x 2 – a x 2 + x 2 – a = √(a 2 +b 2) o x 2 = (√(a 2 +b 2) + a)/2 y y 2 = (√(a 2 +b 2) – a)/2

Raíz cuadrada de un complejo (cont. ) Hay que tomar en cuenta 2 xy = b, es decir x y y deben tener el mismo signo cuando b>0 y de signo distinto cuando b<0. Para b>0 la solución es Y para b<0 es

Ejemplo

Extraer raíces cuadradas i 3 + 4 i 9 + 40 i – 8 – 6 i 16 – 30 i – 2 – 1. 5 i

Resolver la siguiente cuadrática x 2 – (2 + 3 i)x – 1 + 3 i = 0

Resolver x 4 = 119 – 120 i

Representación gráfica Los números complejos son pares ordenados de números reales, por lo tanto podemos representarlos como puntos en el plano xy. Eje imaginario El vector desde O hasta z determina al número complejo z. La longitud del vector es la magnitud del complejo z z = a + bi = (a; b) b O a Eje real

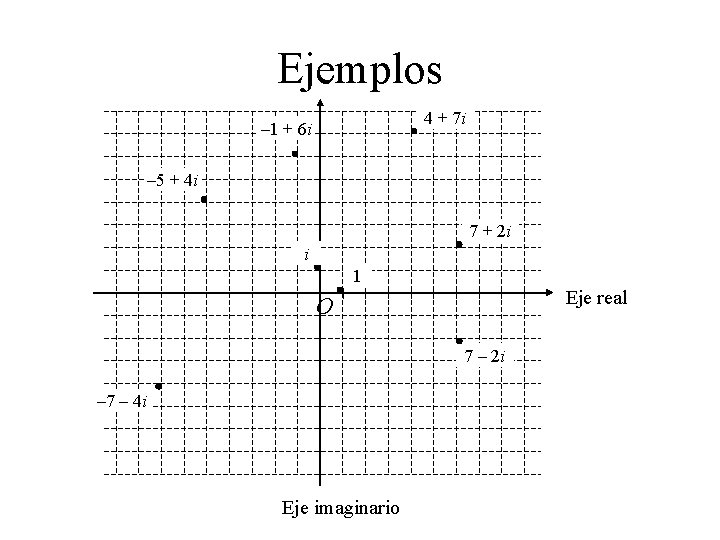
Ejemplos 4 + 7 i – 1 + 6 i – 5 + 4 i 7 + 2 i i 1 Eje real O 7 – 2 i – 7 – 4 i Eje imaginario

Forma trigonométrica z = a + bi = r(cos q + isen q) b = r sen q O a = r cos q Si a>0 y b>0, 0 q p/2 Si a<0 y b>0, p/2 q p Si a<0 y b<0, p q 3 p/2 Si a>0 y b<0, 3 p/2 q 2 p

Convertir a representación trigonométrica 3 + 2 i –√ 6 + 4 i – 4 – √ 3 i 4 – 3 i Convertir a representación rectangular 8(cos 34º + i sen 34º) 5(cos 142º + i sen 142º) 3. 5(cos 245º + i sen 245º) 6(cos 310º + i sen 310º)

Operaciones en forma trigonométrica Sean los complejos A = r 1(cos q 1 + isen q 1) y B = r 2(cos q 2 + isen q 2) El producto A · B es: A·B = r 1 r 2 (cos q 1 + isen q 1)(cos q 2 + isen q 2) = r 1 r 2 (cosq 1 cosq 2+isenq 1 cosq 2+icosq 1 senq 2–senq 2 senq 1 ) = r 1 r 2 (cosq 1 cosq 2–senq 2 senq 1+i(senq 1 cosq 2+cosq 1 senq 2 )) De cosa cosb–sena senb=cos(a+b) y sena cosb+cosa senb = sen(a+b) obtenemos A·B = r 1 r 2 (cos(q 1+q 2) +i(sen(q 1+q 2)) El módulo del producto es igual al producto de los módulos y el argumento del producto es la suma de los argumentos.

Fórmula de De Moivre Si tenemos n factores de la forma (cosq 1 + isenq 1), (cosq 2 + isenq 2), …, (cosqn + isen qn) el producto es (cosq 1+isenq 1)(cosq 2+isenq 2)…(cosqn+isen qn) = cos(q 1+q 2+…+qn) + isen (q 1+q 2+…+qn) Si q = q 1 = q 2 =. . . qn, entonces (cos q + isen q)n = (cos nq + isen nq) Esta identidad es conocida como fórmula de De Moivre. Esta fórmula vale también para exponentes negativos (cos q + isen q)–n = (cos (–nq)+ isen (–nq))

División en forma trigonométrica Sean los complejos A = r 1(cos q 1 + isen q 1) y B = r 2(cos q 2 + isen q 2) El cociente A/B es: A/B = r 1/r 2 (cos q 1 + isen q 1)(cos q 2 + isen q 2)– 1 = r 1/r 2 (cos q 1 + isen q 1)(cos (–q 2)+ isen (–q 2)) Por la regla de la multiplicación A/B = r 1/r 2 (cos(q 1–q 2) +i(sen(q 1–q 2)) El módulo del cociente es igual al cociente de los módulos y el argumento del cociente es la resta de los argumentos del dividendo y el divisor.

Ejercicios Efectuar las operaciones indicadas 3(cos 30º +isen 30º) · 5(cos 70º +isen 70º) 2(cos 57º +isen 57º) · (– 8)(cos 63º +isen 63º) 6(cos 34º +isen 34º) / (– 2. 5(cos 45º +isen 45º)) 9(cos 17º +isen 17º) / 7(cos 123º +isen 123º)

Soluciones trigonométricas Sean A y X dos complejos A = r(cos q 1 + isen q 1) X = R(cos q 2 + isen q 2) La ecuación Xn = A se puede resolver con la fórmula de De Moivre. Xn = Rn(cos nq 2 + isen nq 2) = A = r(cos q 1 + isen q 1) Entonces Rn = r R = n√r Los argumentos de dos complejos son iguales si difieren en un múltiplo 2 p. nq 2 = q 1 + 2 kp

Ejemplo Resolver x 4 = – 4 = 4(cos p + i sen p) x = 41/4(cos((p + 2 kp)/4)+ i sen((p + 2 kp)/4)) Con k = 0, 1, 2, 3 √ 2·(cos(p/4)+ i sen(p/4)) = √ 2(√ 2/2+i√ 2/2) = 1+i √ 2·(cos(3 p/4)+ i sen(3 p/4)) = √ 2(–√ 2/2+i√ 2/2) = – 1+i √ 2·(cos(5 p/4)+ i sen(5 p/4)) = √ 2(–√ 2/2–i√ 2/2) = – 1– i √ 2·(cos(7 p/4)+ i sen(7 p/4)) = √ 2(√ 2/2–i√ 2/2) = 1– i

Ejemplo Resolver x 3 = – 8 i = 4(cos (–p/2) + i sen (–p/2)) x = 41/3(cos((4 k – 1) p/6)+ i sen((4 k – 1) p/6) Con k = 0, 1, 2, 3 2(cos(p/6)+ i sen(p/6)) = √ 3 – i 2(cos(p/2)+ i sen(p/2)) = 2 i 2(cos(7 p/6)+ i sen(7 p/6)) = – √ 3 – i √ 2

Significado geométrico de la operaciones La suma de dos complejos genera un paralelogramo en el plano complejo. La resta es similar a la suma pero el sustraendo sustituido por el negativo.

Significado geométrico de la operaciones (cont. ) La multiplicación puede interpretarse como la construcción de dos triángulos semejantes uno formado por el origen, el extremo del primer factor y el punto (1, 0) y el otro formado por el origen, extremo del segundo factor y extremo del producto. La división tiene una interpretación similar a la multiplicación con dos tríangulos semejantes uno formado por el origen, el extremo del divisor y el punto (1, 0) y el otro formado por el origen, extremo del dividendo y extremo del cociente.

Fórmula de Euler Se puede demostrar que ei q = (cos q + isen q) Todo número complejo a + bi puede escribirse como a + bi = ex + i q = ex(cos q + isen q) = |a + bi| ei q Esta fórmula es conocida como fórmula de Euler. Donde Y