Nilsn Frans Techniques for obtaining pattern Stereographic projection

Nilsén Frans

§ Techniques for obtaining pattern § Stereographic projection § Precession Diffraction § Indexing Single crystals § Indexing Polycrystal § Orientation of Specimen § Computer analysis

§ Core strength is that you can obtain picture and diffraction pattern of the same area in TEM § Currently computers control diffraction pattern formation and indexing § Still important to understand the principles, since computers always give you some results even nonsense results § Multiple techniques depending on what you want to study and how big is grain size: § SAD (Grain sizes 100 nm to 10µm) § CBED (Grain sizes 10 nm to 100 nm) § Texture (Grain size below 10 nm) § In this lecture we concentrate on SADP

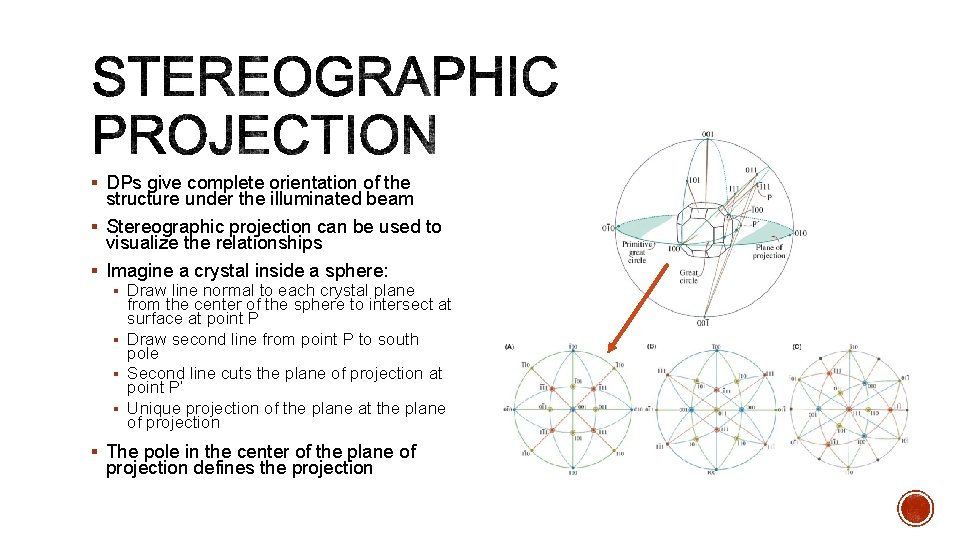
§ DPs give complete orientation of the structure under the illuminated beam § Stereographic projection can be used to visualize the relationships § Imagine a crystal inside a sphere: § Draw line normal to each crystal plane from the center of the sphere to intersect at surface at point P § Draw second line from point P to south pole § Second line cuts the plane of projection at point P’ § Unique projection of the plane at the plane of projection § The pole in the center of the plane of projection defines the projection

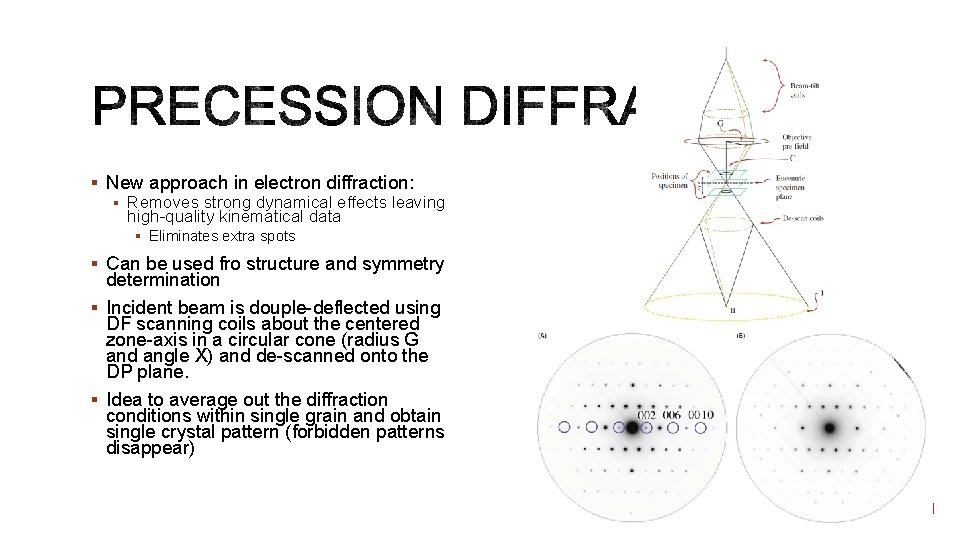
§ New approach in electron diffraction: § Removes strong dynamical effects leaving high-quality kinematical data § Eliminates extra spots § Can be used fro structure and symmetry determination § Incident beam is douple-deflected using DF scanning coils about the centered zone-axis in a circular cone (radius G and angle X) and de-scanned onto the DP plane. § Idea to average out the diffraction conditions within single grain and obtain single crystal pattern (forbidden patterns disappear)

§ Basic rule: § Rd=λL § As λL is constant R 1 d 1=R 2 d 2=R 3 d 3… § If lattice parameters are known = allowed reflections are known (Table 18. 1) § Idea: § Identify possible g 1 and g 2 § Calculate angles between g 1 and g 2 § Angle between planes is φ and angle between directions is ρ § REMEMBER check that s= 0 in TEM § Method: § Tilt sample to low-index pole § Set s = 0 § Record DP § Repeat with higher-order reflections

§ Diffraction from polycrystals (nanoscale grains) = x-ray diffraction from powders § Reciprocal lattice rotated about all axes to produce set of nested spheres intersected with Ewald spheres § If textured then one special plane is common (distinguished by tilting sample rings become arcs) § Grain size affects the continuity in ring pattern can be estimated based on the width of the rings

§ Once three vectors (g 1, g 2 and g 3) are known beam direction can be calculated (determinant should be positive) § Electron beam travels along direction –B § Once DP is indexed and B is determined the orientation relationships (OR) can be calculated § OR determine how well the atomic planes in two phases fit together controls interphase interface (coherent/incoherent) dislocation interaction on boundary mechanical behaviour

§ Most likely indexing done with computer using standard reference sources § Approach requires to collect all the data you can search through the ICDD powder diffraction files or some other database § Important rules to remember: § Measurements made on calibrated SADP will be accurate to 1 -2% not more § Check multiple domains and double diffraction first § Strategy to search and match has been given by Lyman and Carr, idea is to find all possible matches and then use other data fro example compositional to make final identification § Remember to simulate DPs to confirm that the software package reproduce what you see!