Niezwyke efekty w pobliu czarnych dziur Czarna dziura

Niezwykłe efekty w pobliżu czarnych dziur

Czarna dziura: co to jest? Rozwiązanie sferycznie symetryczne (statyczne, Karl Schwarzschild 1916) Metryka: Promień grawitacyjny: (Dla przykładu: promień grawitacyjny Ziemi ~ 1 cm) W przypadku czarnej dziury Schwarzschilda w odległości r=rg od środka znajduje się horyzont

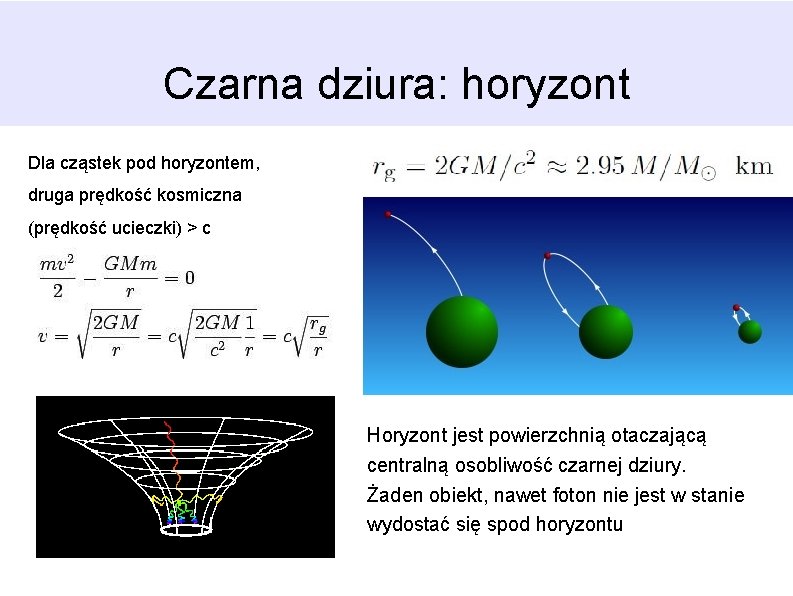
Czarna dziura: horyzont Dla cząstek pod horyzontem, druga prędkość kosmiczna (prędkość ucieczki) > c Horyzont jest powierzchnią otaczającą centralną osobliwość czarnej dziury. Żaden obiekt, nawet foton nie jest w stanie wydostać się spod horyzontu

Horyzont a powierzchnia

Rozwiązanie Kerra Rozwiązanie osiowo-symetryczne (rotująca czarna dziura, Roy Kerr 1963): Czarna dziura opisana przez dwa parametry: masę M oraz moment pędu J

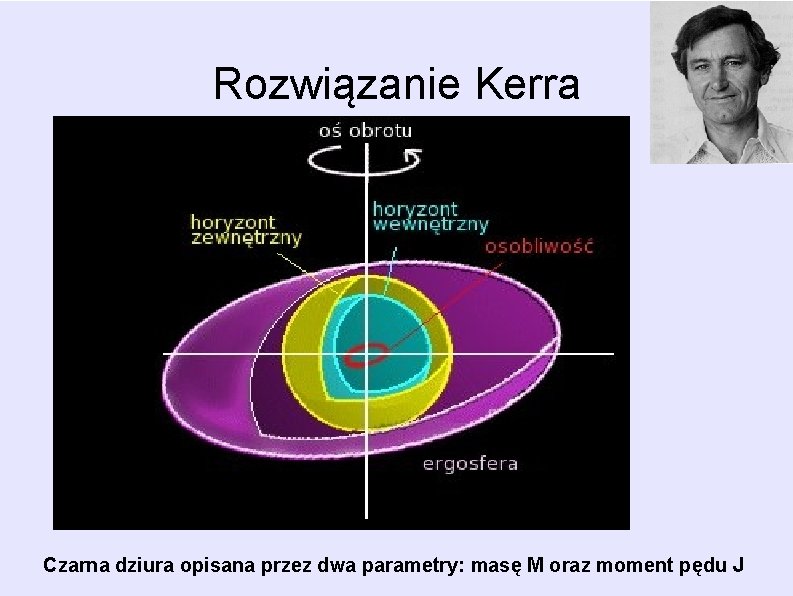
Rozwiązanie Kerra Czarna dziura opisana przez dwa parametry: masę M oraz moment pędu J

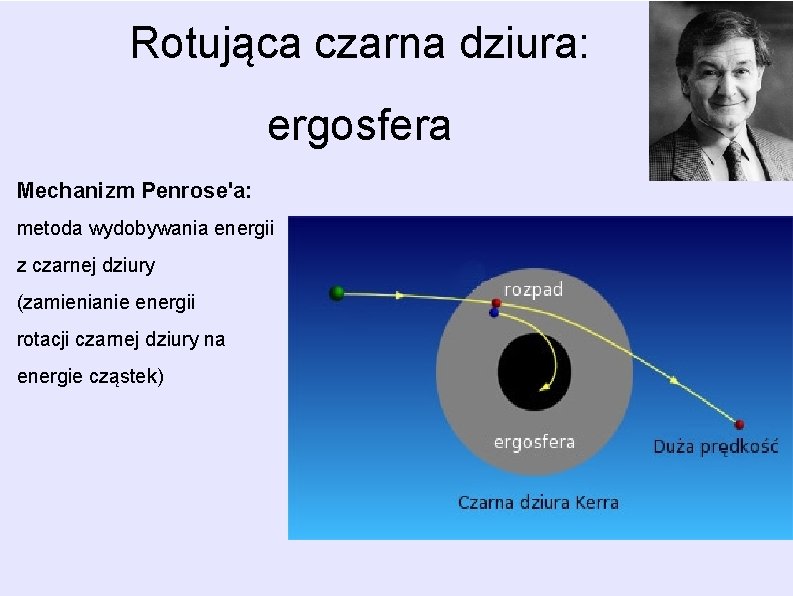
Rotująca czarna dziura: ergosfera Mechanizm Penrose'a: metoda wydobywania energii z czarnej dziury (zamienianie energii rotacji czarnej dziury na energie cząstek)

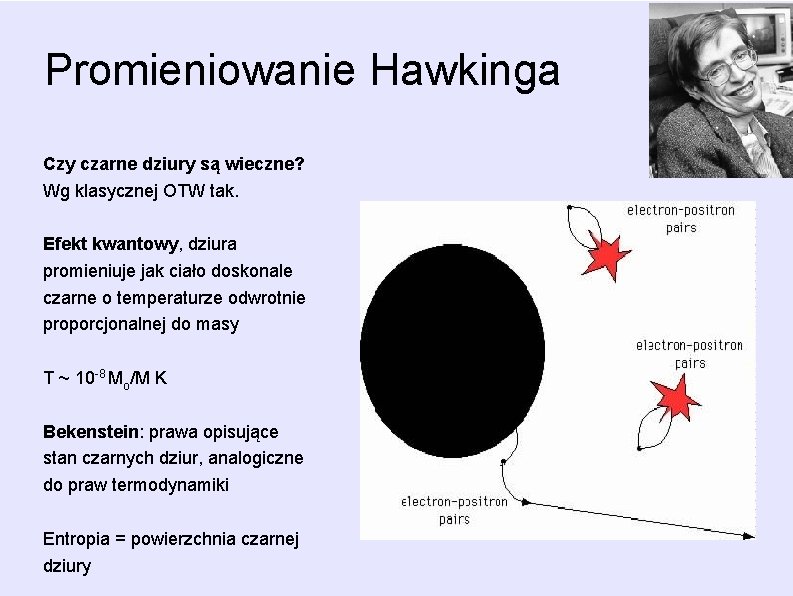
Promieniowanie Hawkinga Czy czarne dziury są wieczne? Wg klasycznej OTW tak. Efekt kwantowy, dziura promieniuje jak ciało doskonale czarne o temperaturze odwrotnie proporcjonalnej do masy T ~ 10 -8 Mo/M K Bekenstein: prawa opisujące stan czarnych dziur, analogiczne do praw termodynamiki Entropia = powierzchnia czarnej dziury

Schwarzschild vs Kerr Rotująca czarna dziura jest mniejsza od statycznej!

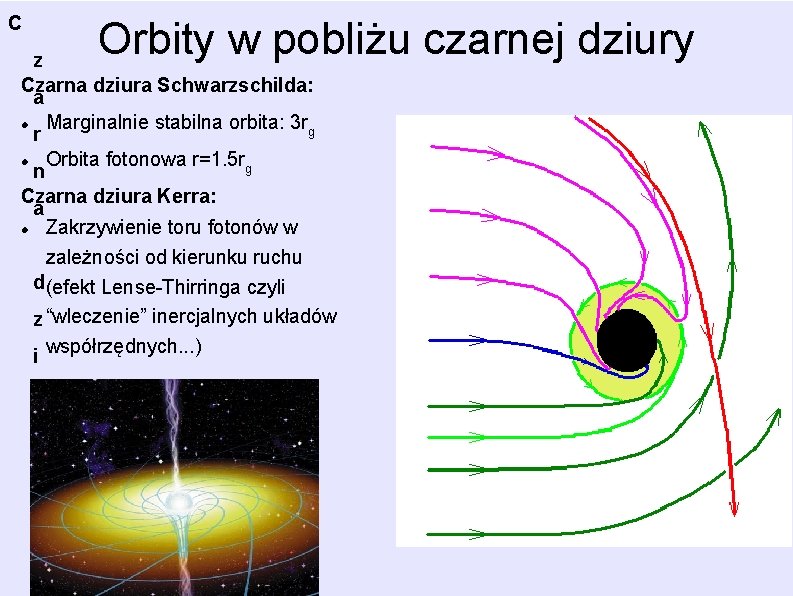
C Orbity w pobliżu czarnej dziury z Czarna dziura Schwarzschilda: a Marginalnie stabilna orbita: 3 rg r Orbita fotonowa r=1. 5 rg n Czarna dziura Kerra: a Zakrzywienie toru fotonów w zależności od kierunku ruchu d(efekt Lense-Thirringa czyli z “wleczenie” inercjalnych układów współrzędnych. . . ) i u r a S c

Czarna dziura w centrum Galaktyki Masa: 2. 6± 0. 2 106 Mo, promień ~ 120 AU Sgr A*: silne źródło promieniowania radiowego

Czarna dziura w centrum Galaktyki Obserwacje ruchu gwiazd w okolicy: pomiar masy klasycznymi metodami astronomii układów podwójnych

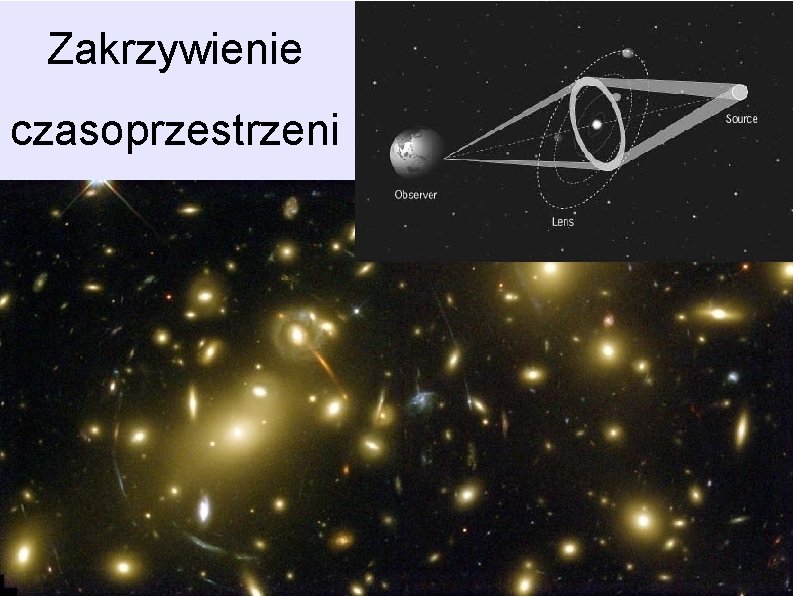
Zakrzywienie czasoprzestrzeni

Teoria Newtona

( r g = 0. 5 m z o d l e g ł o Teoria Einsteina

Na orbicie wokół czarnej dziury Symulacja hipotetycznego układu poczwórnego, którego składnikiem jest czarna dziura

Na orbicie wokół czarnej dziury Orbita: 2 promienie Schwarzschilda (2 rg)

Na orbicie wokół czarnej dziury

Spadek na czarną dziurę

Spadek na czarną dziurę Spadek z nieskończoności pod horyzont

“Najlżejsza” czarna dziura (3. 8 Mo) XTE J 1650 -500 (niebo południowe, konst. Ołtarz) Pomiar masy poprzez częstość kwaziperiodycznych oscylacji Ograniczenie na maksymalną masę gwiazd neutronowych. . .

“Średnio-masywna” czarna dziura 40000 Mo w gromadzie kulistej Omega Centauri Analiza ruchu gwiazd w centrum: niewidoczne centrum przyciągania, czyli prawdopodobnie centralna czarna dziura. . . Potwierdzenie ciągłości rozkładu funkcji mas czarnych dziur, od mas gwiazdowych do supermasywnych ~106 - 1010 Mo